整数规划基本原理
1.1 定义
规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法,往往只适用于整数线性规划。目前还没有一种方法能有效地求解一切整数规划。

整数规划问题的特点在于其决策变量含有整数变量


摘自于【整数规划(一)】整数规划问题综述 (zhihu.com)
:
一般来说,之所以在模型中要引入整数变量主要原因有2点:
1 我们所需要描述的变量来自生活实际,而这些变量都是整数的。例如:要表示 多少架飞机,多少辆汽车,多少个人 等等 这些变量必然只能是整数的,这些实际问题中的变量若取分数则失去了实际意义,因此我们必须用整数变量来进行建模。
2 我们要描述逻辑,Yes 或者 No,乃至于更复杂的逻辑关系。我们经常会用1代表Yes,0代表No,从这里也可以衍生出很多复杂的逻辑关系。值得注意的是区别于前一种情况此时的整数变量看起来貌似还是整数的形式,但实际上准确的来说说 它们已经是 Bool 变量了。Bool 变量满足 Bool 变量的运算法则,例如 与或非这些,而不满足加减乘除的运算规则。明白了这一点对整数规划问题的建模有着很大的帮助。
分类:


求解方法
分支定界算法求解整数线性规划问题
第一个是穷举法,浪费时间空间
分支定界法:先求出相应松弛问题的最优解
若松弛问题无可行解,则 ILP 无可行解
若松弛问题最优解符合整数要求,则是最优解
若不满足整数条件,则任选一个不满足整数条件的变量x来构造心得约数添加到松弛问题形成两个子问题,依次在减小的可行域求解新的最优解,并重复,直到子问题无解,或整数有最优解。
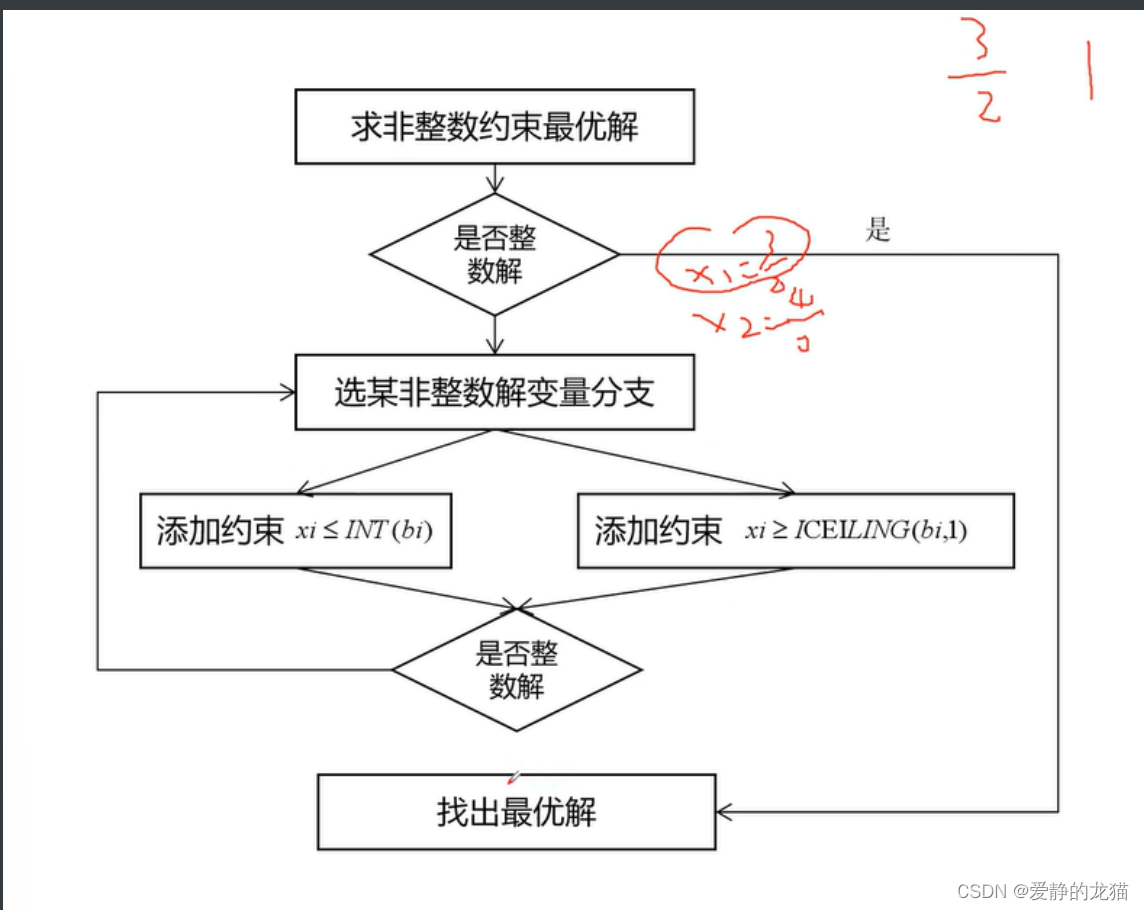
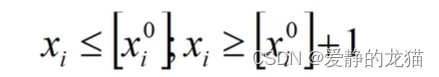
再谈分支定界,增强理解

上界缩小,下界增大,直到求出为止。
步骤一:确定初始定界,求解线性规划B的最优解,作为初始上界,求解A的一个整数解,作为初始下界。
步骤二:选择B最优解不满足整数条件的变量,约束B为两个子问题,求出B1,B2的最优解
步骤三:比较各分支的解,将最优目标函数值的最大值作为下界,将各分支整数条件的最大值作为新的下界。
步骤四:剪枝,比较各分支的解,若小于新的下界,则剪枝,若无可行解,剪枝,若大于新的下界,那么重复2,3,4.
按照以上步骤不断更新即可。
割平面法的基本思想


割掉的部分只包含非整数解。
步骤一:将约束条件中的系数和常熟化为整数,然后采用单纯形法求解不考虑整数约束的线性规划问题的最优解。
步骤二:在最终单形法中选择一个非整数基变量所在的约束等式,将该约束等式的系数和常熟分解为整数和非真分数之和。
步骤三:将所有整数部分放在左边,分数放在右边,根据各变量的约束特点分析等式右边,得到切割方程。
步骤四:将切割方程代入线性规划问题的最终表中求解最优解,若仍然未得到最优整数解,重述步骤二到步骤四。


0-1规划


常用约束条件的表达方式

隐枚举法
求解思路及改进措施:
(1) 先试探性求一个可行解,易看出(x1, x2 , x3 ) = (1,0,0) 满足约束条件,故为一个可行解,且 z = 3。
(2) 因为是求极大值问题,故求最优解时,凡是目标值 z < 3的解不必检验是否满足约束条件即可删除,因它肯定不是最优解,于是应增加一个约束条件(目标值下界):
(3) 改进过滤条件。
(4)由于对每个组合首先计算目标值以验证过滤条件,故应优先计算目标值 z 大的组合,这样可提前抬高过滤门槛,以减少计算量。
指派问题--匈牙利算法
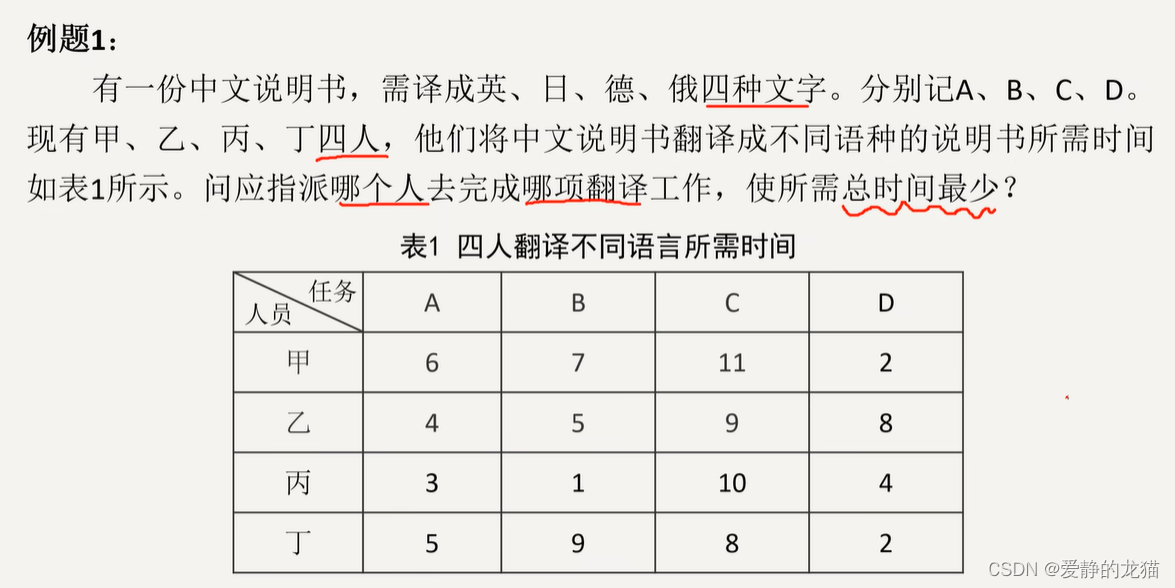

指派问题模型引入

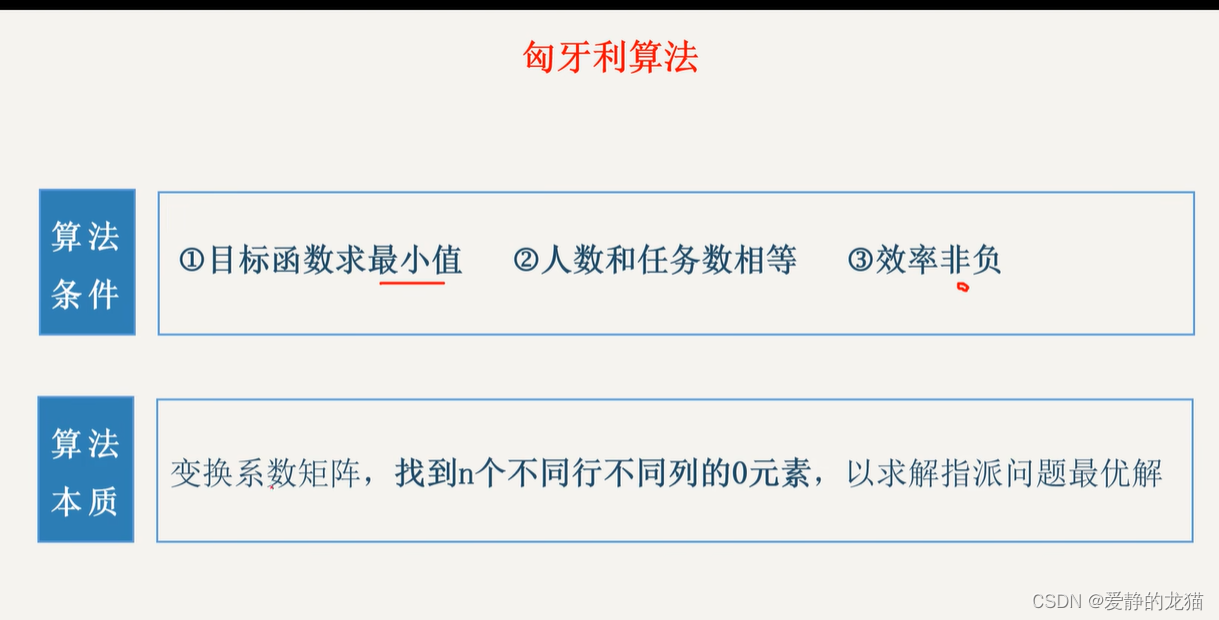
匈牙利算法步骤:
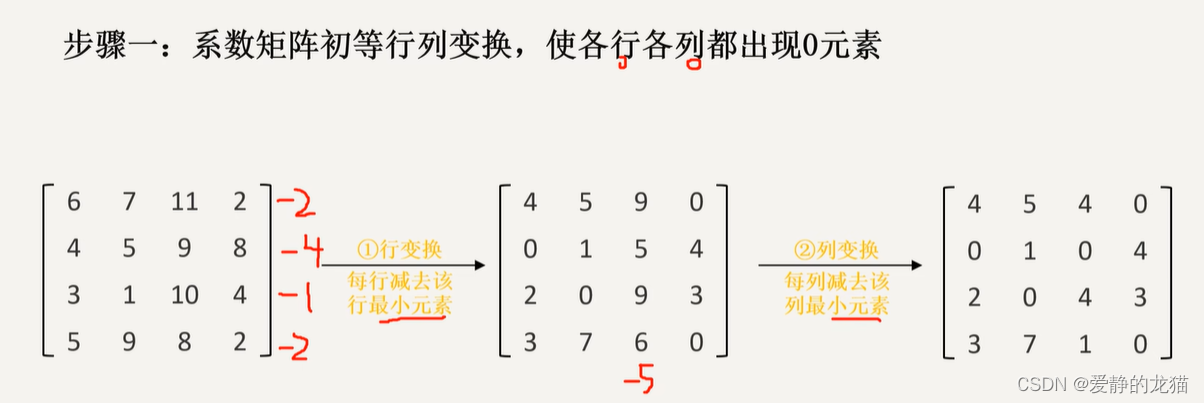
步骤一:系数矩阵初等行变换,再进行初等列变换,使得各行各列出现0元素。
注意,减去的是最小值。
步骤二:找到只有一个0元素的行,花圈,划去该列其他0元素
同理,再对列做这件事清

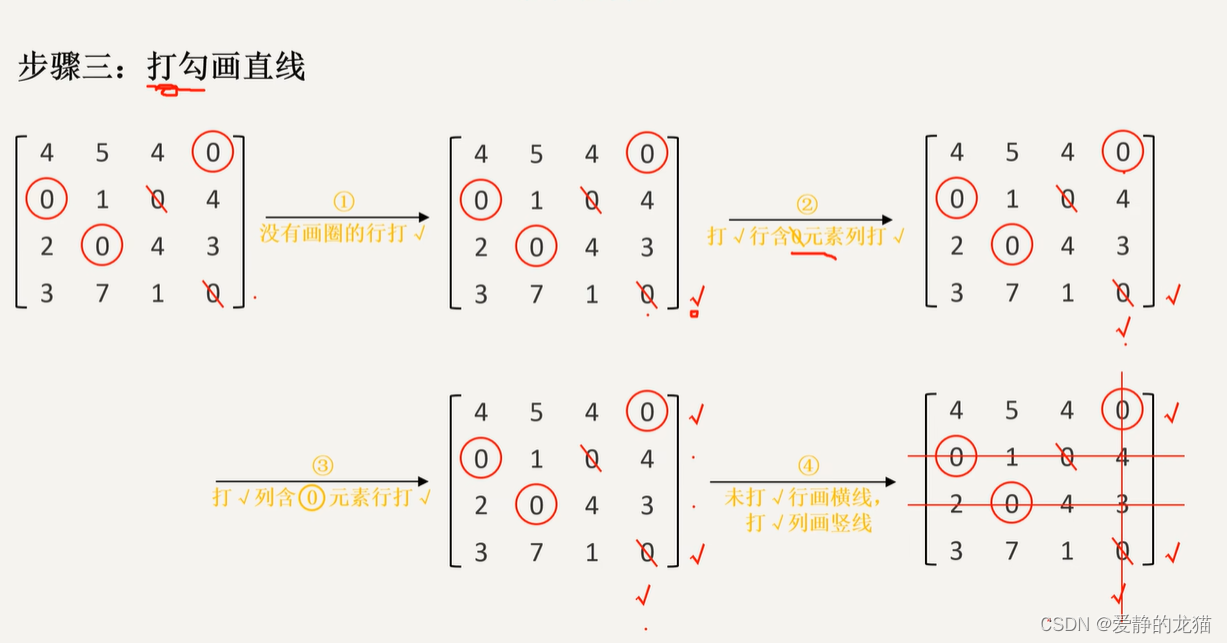
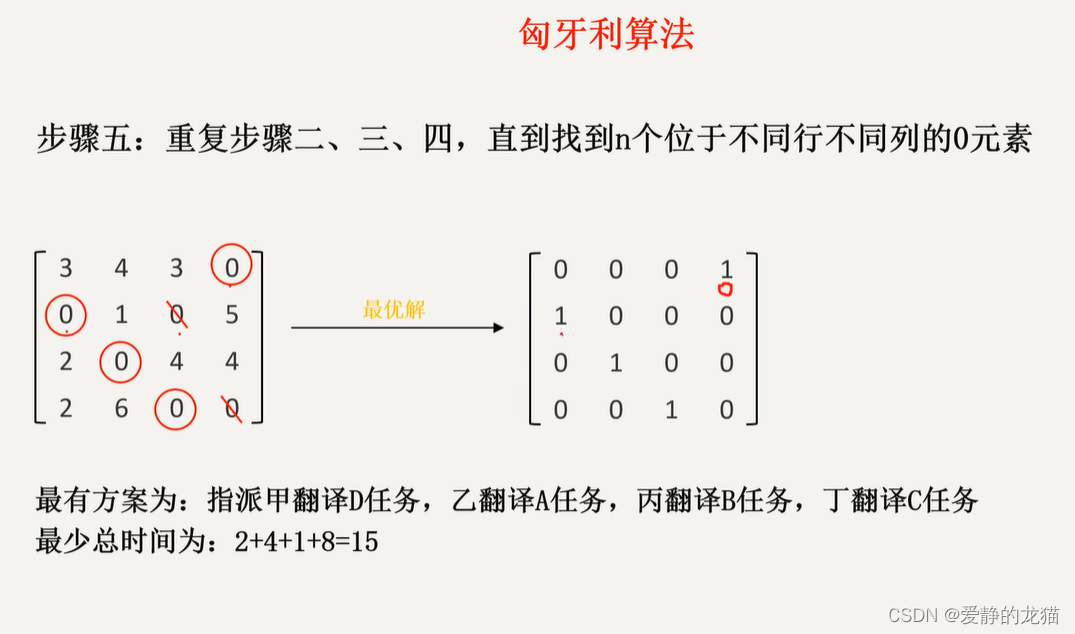
步骤三:
相关文章:

整数规划基本原理
1.1 定义 规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法,往往只适用于整数线性规划。目前还没有一种方法…...

秋招复习之堆
目录 前言 堆 堆的常用操作 堆的实现(大根堆) 1. 堆的存储与表示 2. 访问堆顶元素 3. 元素入堆 4. 堆顶元素出堆 Top-k 问题 方法一:遍历选择 方法二:排序 方法三:堆 总结 前言 秋招复习之堆。 堆 「堆 heap…...
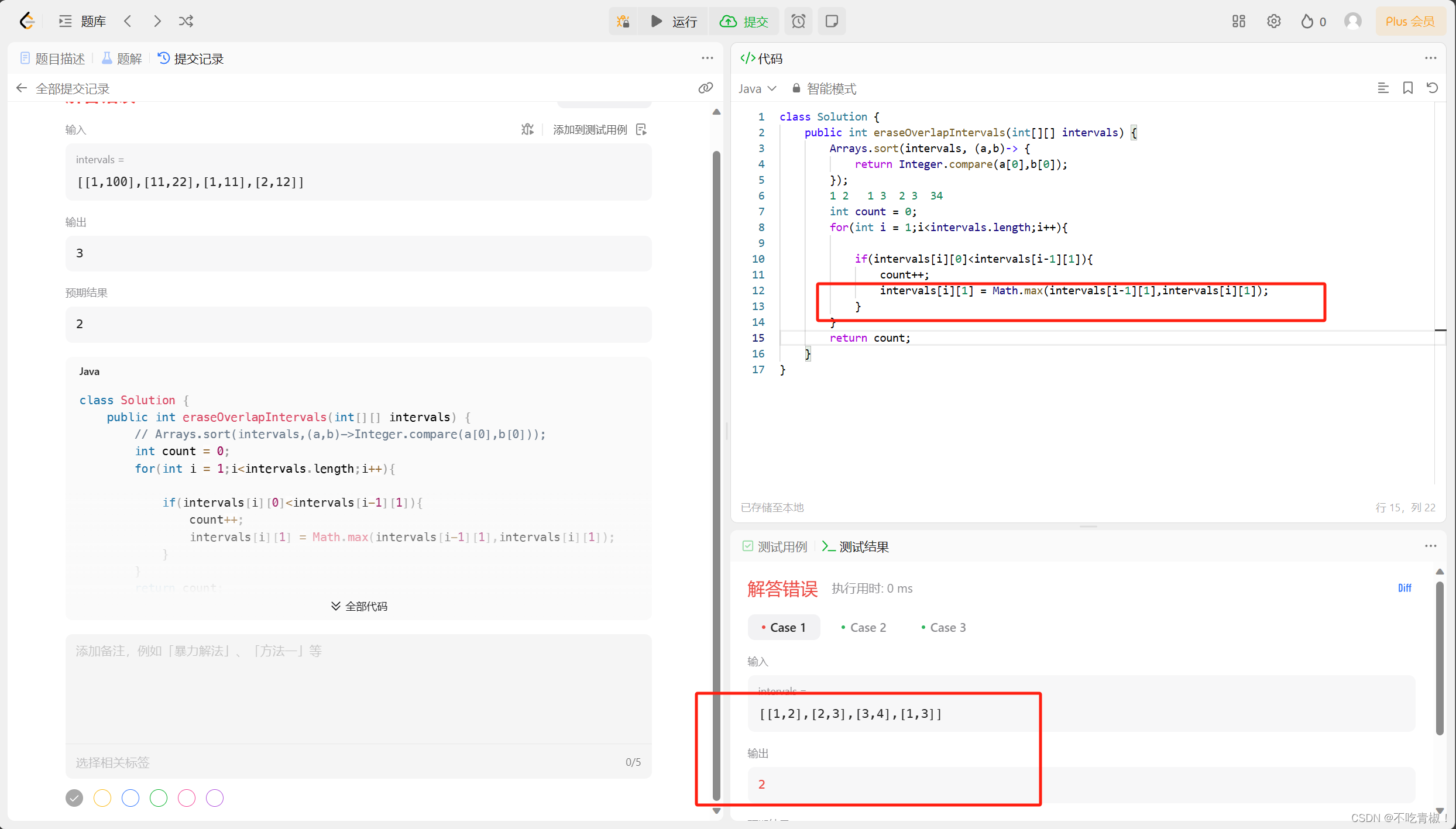
算法训练营Day36(贪心-重叠区间)
都算是 重叠区间 问题,大家可以好好感受一下。 都属于那种看起来好复杂,但一看贪心解法,惊呼:这么巧妙! 还是属于那种,做过了也就会了,没做过就很难想出来。 不过大家把如下三题做了之后&#…...

如何利用Oracle官方网站不登录账号下载和安装非最新版本的JDK(版本自由选择)
一、JDK概述 JDK(Java Development Kit)是Java开发工具集,是针对Java编程语言的软件开发环境。它包含了Java编译器、JRE(Java运行时环境)以及其他一些用于开发、调试和测试Java应用程序的工具,是Java开发人…...
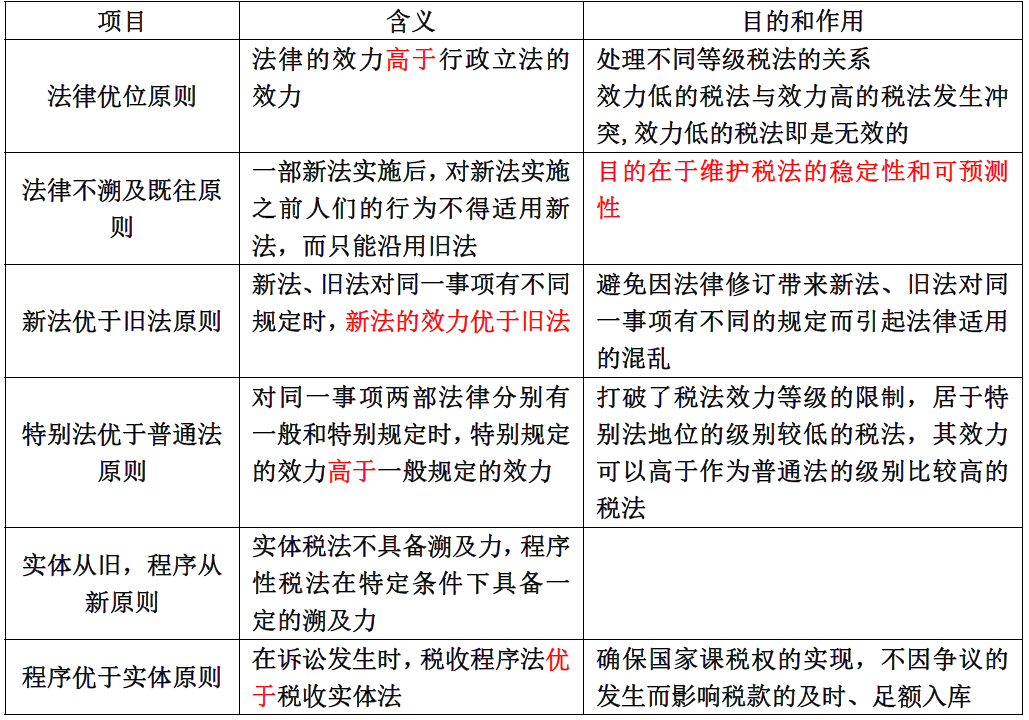
税法相关的基础知识
文章目录 税法原则1.税法基本原则2.税法适用原则 来和大家聊聊税法相关的基础知识 税法原则 1.税法基本原则 2.税法适用原则...

ListNode 2487. 从链表中移除节点,单调栈的应用
一、题目 1、题目描述 给你一个链表的头节点 head 。 移除每个右侧有一个更大数值的节点。 返回修改后链表的头节点 head 。 2、接口描述 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nu…...
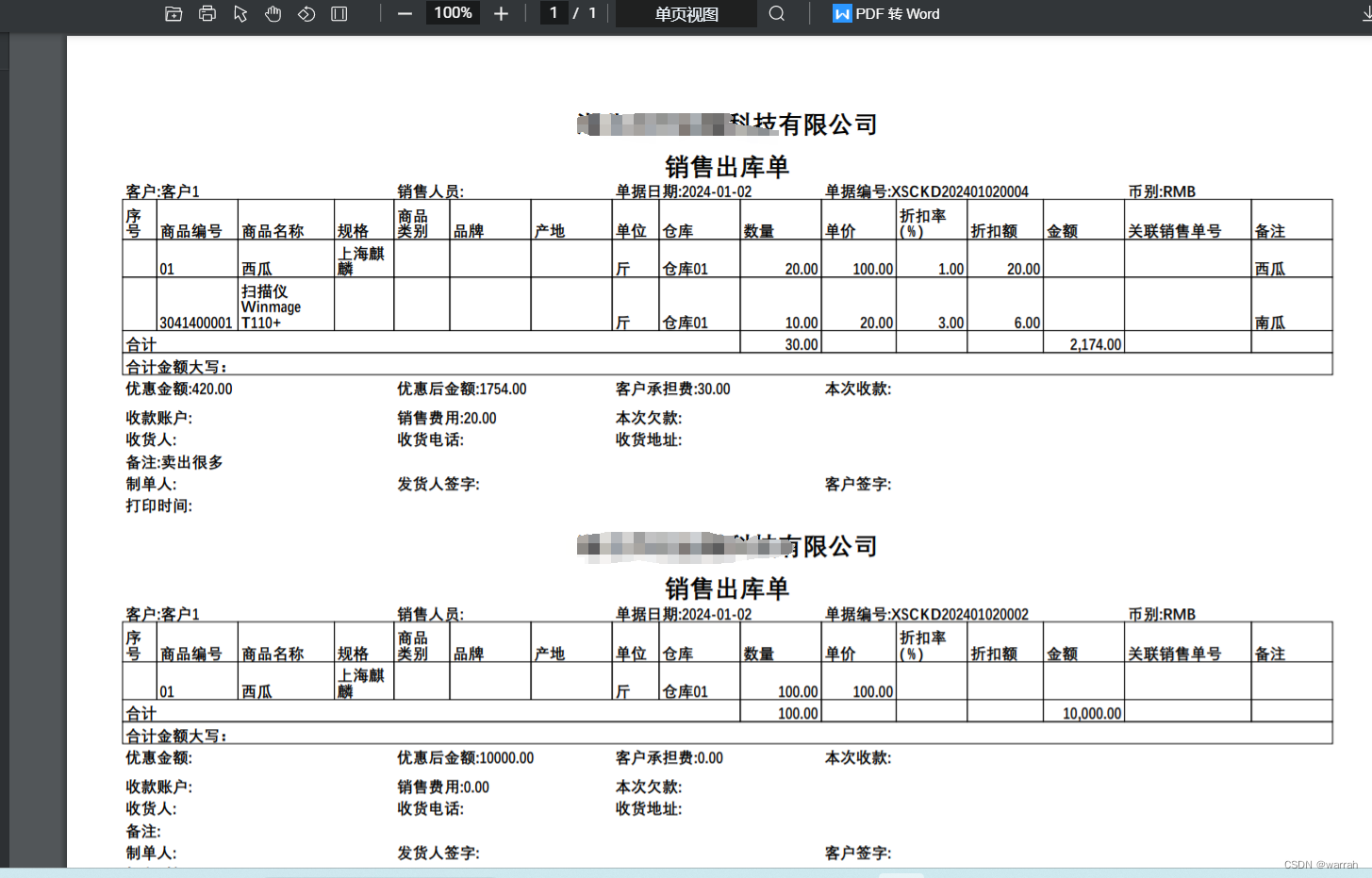
vue3中pdf打印问题处理
1 get请求参数问题 之前的请求是post得不到参数,今天发现的问题很奇怪,从前端进入网关,网关居然得不到参数。 前端代码 const print () > {let linkUrlStr proxy.$tool.getUrlStr(proxy.$api.invOrder.psiInvOrder.printSalOutstock,{a…...
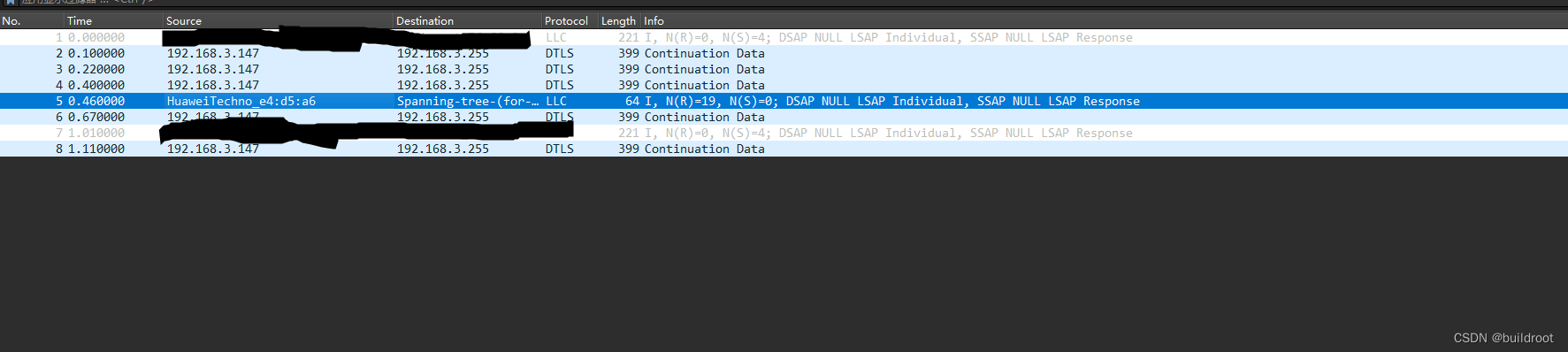
如何向嵌入式设备中添加tcpdump工具
说明:tcpdump是一个在网络设备调试中一个非常重要的工具,它并不像hexdump等工具集成在busybox里面,也不像其他的软件一样只需要依赖linux标准的库就可以实现,它需要pcap相关的库和加密的相关库。 本文主要是基于realtek 83系列的…...

伦茨科技Apple Find My认证芯片-ST17H6x芯片
深圳市伦茨科技有限公司(以下简称“伦茨科技”)发布ST17H6x Soc平台。成为继Nordic之后全球第二家取得Apple Find My「查找」认证的芯片厂家,该平台提供可通过Apple Find My认证的Apple查找(Find My)功能集成解决方案。…...
uni-app 前后端调用实例 基于Springboot 数据列表显示实现
锋哥原创的uni-app视频教程: 2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中..._哔哩哔哩_bilibili2023版uniapp从入门到上天视频教程(Java后端无废话版),火爆更新中...共计23条视频,包括:第1讲 uni…...

python渗透工具编写学习笔记:10、网络爬虫基础/多功能编写
目录 前言 10.1 概念 10.2 调度器/解析器 10.3 存储器/去重器 10.4 日志模块 10.5 反爬模块 10.6 代理模块 前言 在渗透工具中,网络爬虫有着不可忽视的作用,它能够快速而精准的搜寻、提取我们所需要的信息并按照我们所需要的格式排列,…...
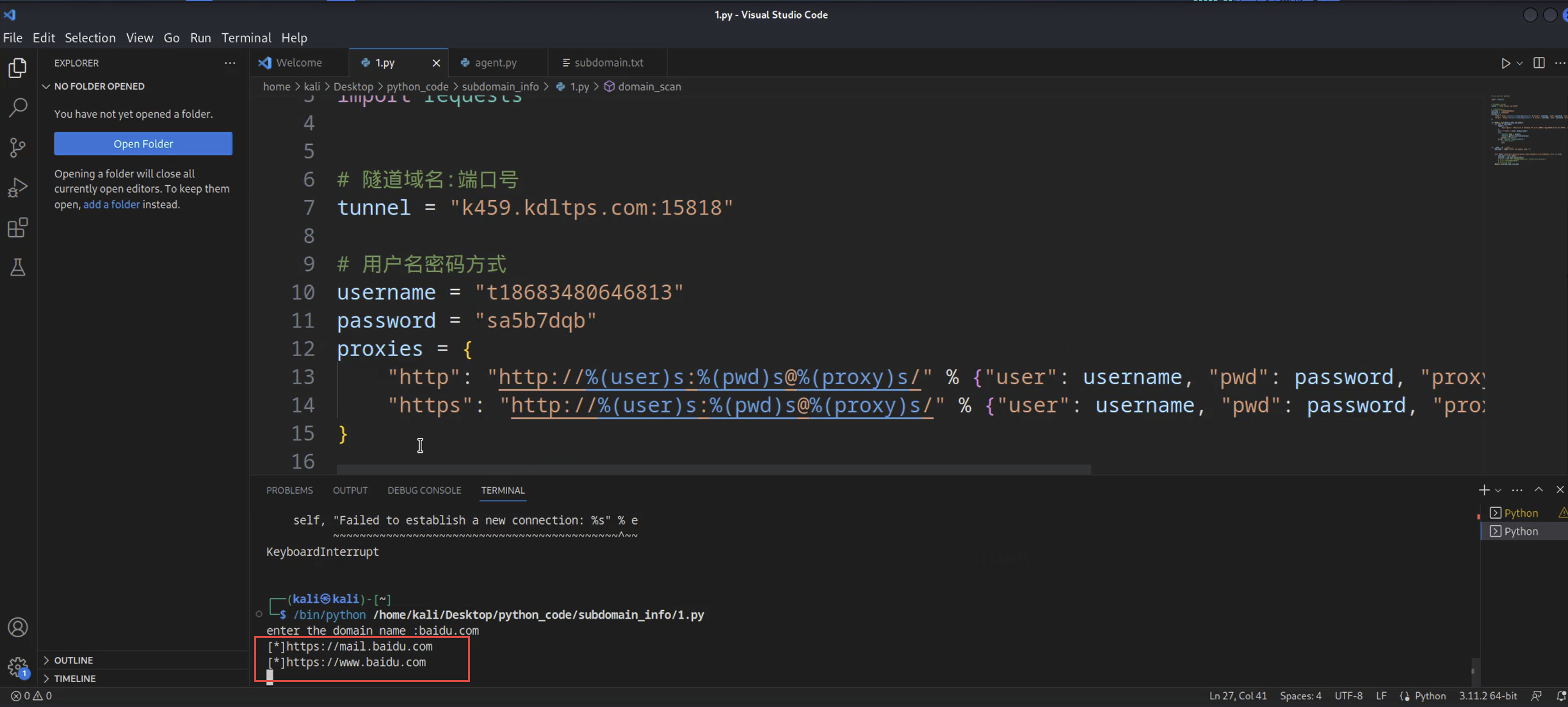
Python武器库开发-武器库篇之子域名扫描器开发(四十一)
Python武器库开发-武器库篇之子域名扫描器开发(四十一) 在我们做红队攻防或者渗透测试的过程中,信息收集往往都是第一步的,有人说:渗透的本质就是信息收集,前期好的信息收集很大程度上决定了渗透的质量和攻击面,本文将…...

通俗易懂的15个Java Lambda表达式案例
文章目录 1. **实现Runnable接口**:2. **事件监听器**(如Swing中的ActionListener):3. **集合遍历**(使用forEach方法):4. **过滤集合**(使用Stream API):5. …...
)
十七:爬虫-JS逆向(上)
1、什么是JS、JS反爬是什么?JS逆向是什么? JS:JS全称JavaScript是互联网上最流行的脚本语言,这门语言可用于HTML 和 web,更可广泛用于服务器、PC、笔记本电脑、平板电脑和智能手机等设备。JavaScript 是一种轻量级的编程语言。JavaScript 是…...

How to implement anti-crawler strategies to protect site data
How to implement anti-crawler strategies to protect site data 信息校验型反爬虫User-Agent反爬虫Cookie反爬虫签名验证反爬虫WebSocket握手验证反爬虫WebSocket消息校验反爬虫WebSocket Ping反爬虫 动态渲染反爬虫文本混淆反爬虫图片伪装反爬虫CSS偏移反爬虫SVG映射反爬虫字…...

王国维的人生三境界,这一生至少当一次傻瓜
一、人生三境界 古今之成大事业、大学问者,必经过三种之境界。“昨夜西风凋碧树,独上高楼,望尽天涯路。”此第一境也。“衣带渐宽终不悔,为伊消得人憔悴。”此第二境也。“众里寻他千百度,蓦然回首,那人却…...
Jmeter二次开发实操问题汇总(JDK问题,jar包问题)
前提 之前写过一篇文章:https://qa-lsq.blog.csdn.net/article/details/119782694 只是简单尝试了一下生成一个随机手机号码。 但是如果在工作中一个实际场景要用的二次开发,可能会遇到一些问题。 比如这样一个场景: Mobile或者前端调用部分…...

网络安全B模块(笔记详解)- 数字取证
数据分析数字取证-attack 1.使用Wireshark查看并分析Windows 7桌面下的attack.pcapng数据包文件,通过分析数据包attack.pcapng找出恶意用户的IP地址,并将恶意用户的IP地址作为Flag(形式:[IP地址])提交; 解析:http.request.method==POST Flag:[172.16.1.102] 2.继续…...
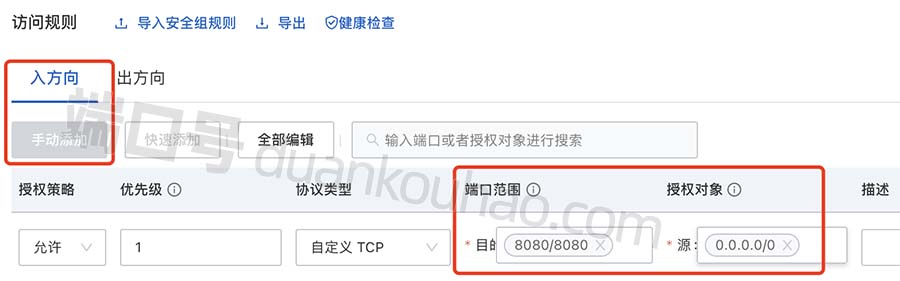
阿里云服务器8080端口安全组开通图文教程
阿里云服务器8080端口开放在安全组中放行,Tomcat默认使用8080端口,8080端口也用于www代理服务,阿腾云atengyun.com以8080端口为例来详细说下阿里云服务器8080端口开启教程教程: 阿里云服务器8080端口开启教程 阿里云服务器8080端…...
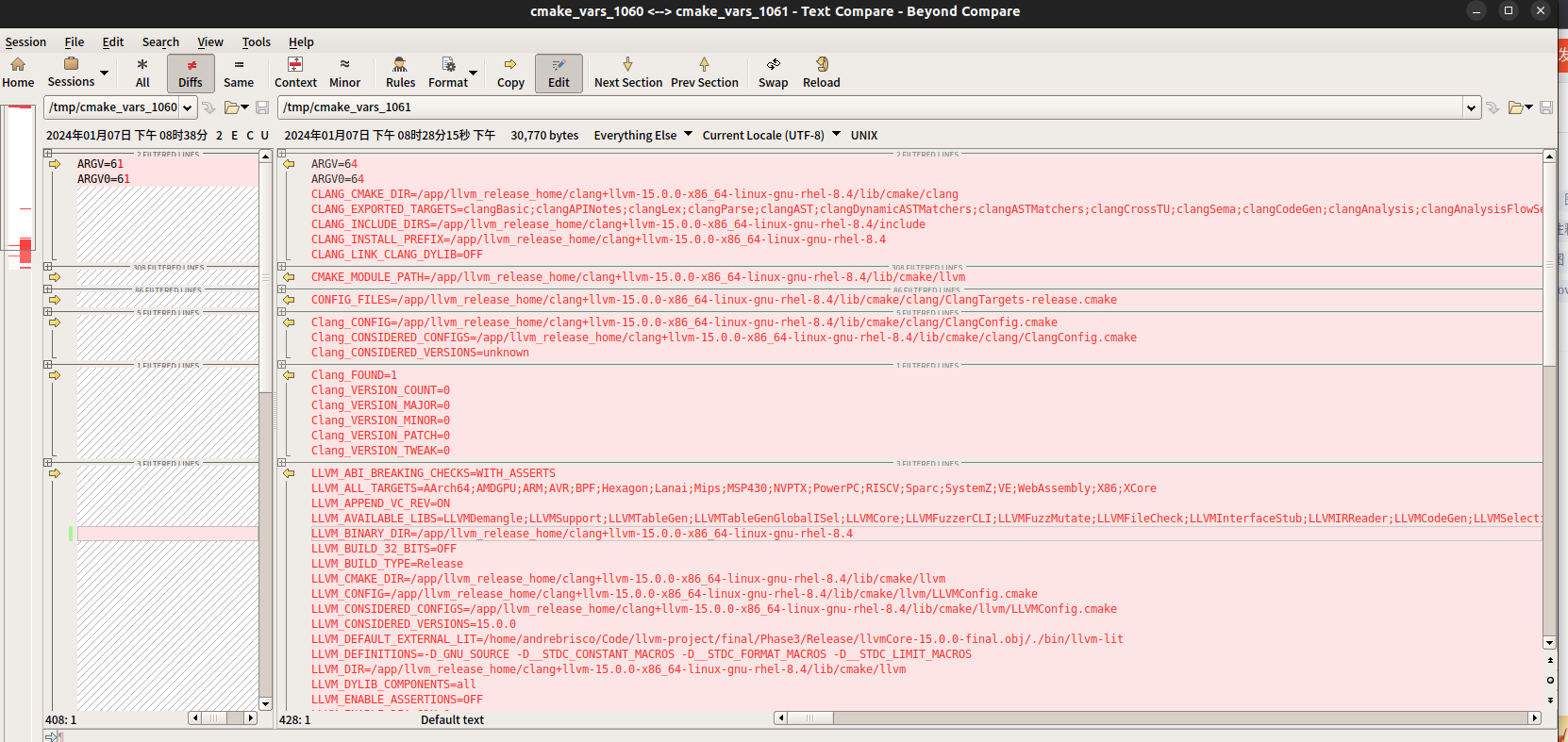
vmlinux, vmlinux.bin, bzImage; cmake的find_package(Clang)新增了哪些变量( 比较两次记录的所有变量差异)
vmlinux, vmlinux.bin, bzImage cd /bal/linux-stable/ file vmlinux #vmlinux: ELF 32-bit LSB executable, Intel 80386, version 1 (SYSV), statically linked, BuildID[sha1]=b99bbd9dda1ec2751da246d4a7ae4e6fcf7d789b, not stripped #文件大小 20MB, 19940148Bfile ar…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
