day10 用栈实现队列 用队列实现栈
题目1:232 用栈实现队列
题目链接:232 用栈实现队列
题意
用两个栈实现先入先出队列(一个入栈,一个出栈),实现如下功能:
1)push:将元素x推到队列末尾
2)pop:从队列的开头移除并返回元素
3)peek:返回队列开头的元素
4)empty:若队列为空,返回true,否则,返回false

代码
class MyQueue {
public:stack<int> stackIn;//入栈stack<int> stackOut;//出栈MyQueue(){}void push(int x){stackIn.push(x);}int pop(){//stackOut出栈为空时,放入元素if(stackOut.empty()){while(!stackIn.empty()){stackOut.push(stackIn.top());stackIn.pop();}}//出栈不为空时,直接弹出元素int result = stackOut.top();stackOut.pop();return result;}int peek(){int result = this->pop();//复用上面的pop()函数,stackOut.push(result);//但是还需要将元素放回出栈中return result;}bool empty(){return (stackIn.empty() && stackOut.empty());}};/*** Your MyQueue object will be instantiated and called as such:* MyQueue* obj = new MyQueue();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->peek();* bool param_4 = obj->empty();*/- 时间复杂度: push和empty为O(1), pop和peek为O(n)
- 空间复杂度: O(n)
题目2: 225 用队列实现栈
题目链接:225 用队列实现栈
题意
使用两个队列实现栈,实现如下功能
push:将元素x压入栈顶
pop:移除并返回栈顶的元素
top:返回栈顶的元素
empty:栈为空,返回true,否则,返回false
两个队列
其中一个队列(que2)用来备份,把que1要弹出的元素以外的元素都备份到que2,然后弹出que1中的那个元素,再将que2中的元素放到que1中,同时清空que2

逻辑
例1:que2每次都要清空
每pop一次,que2都要备份一次,一定要是空的,才能接续不断地进行操作,如果不清空的话,有可能已经弹出的元素会再次回到栈中

例2:que2的全部元素都要移动到que1中
因为que2中保存的是当前pop操作que1中没有用到的元素,为了保证后续操作,要将que2中的全部元素移动到que1中。

代码
class MyStack {
public:queue<int> que1;queue<int> que2;MyStack(){}void push(int x){que1.push(x);}int pop(){int size = que1.size();size--;while(size--){que2.push(que1.front());//que2备份que1弹出的元素que1.pop();}int result = que1.front();que1.pop();//que1 = que2while(!que2.empty()){que1.push(que2.front());que2.pop();}return result;}int top(){return que1.back();}bool empty(){return que1.empty();}
};/*** Your MyStack object will be instantiated and called as such:* MyStack* obj = new MyStack();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->top();* bool param_4 = obj->empty();*/- 时间复杂度: pop为O(n),其他为O(1)
- 空间复杂度: O(n)
一个队列(★)
模拟出栈时,将队列头部(出)的size-1个元素依次重新添加到队尾(入),剩下的那个没有移动的元素就是所求
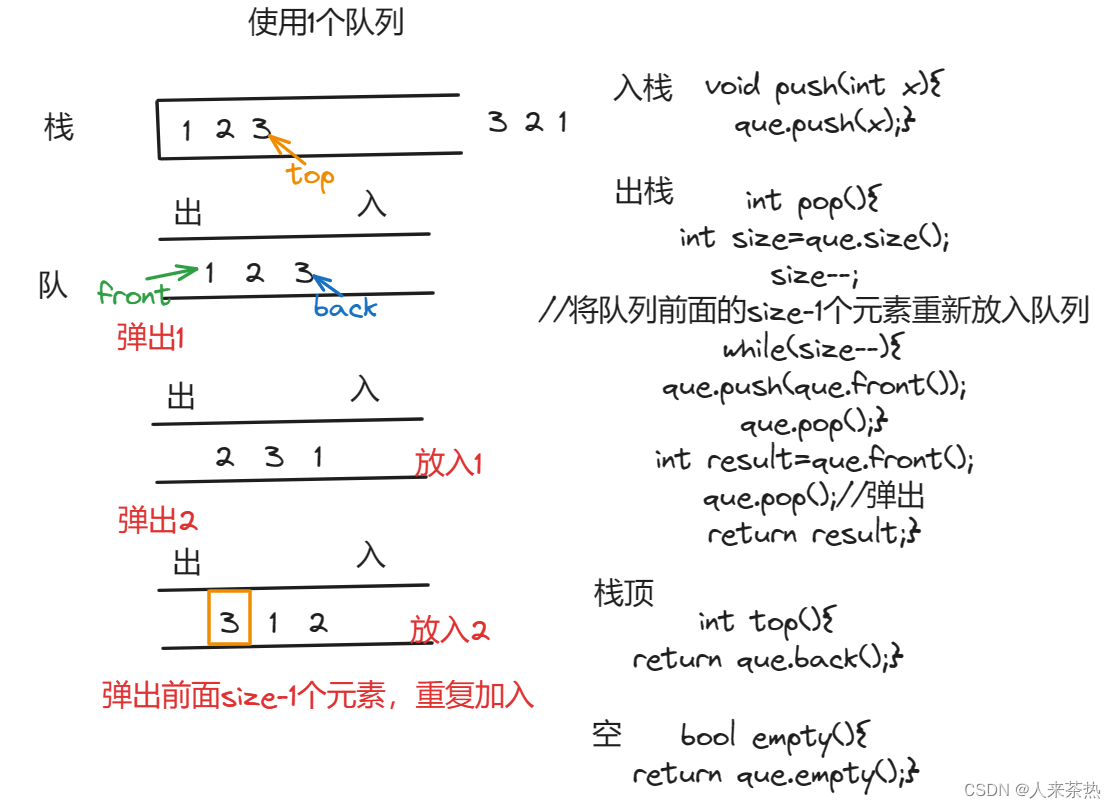
代码
class MyStack {
public:queue<int> que;MyStack(){}void push(int x){que.push(x);}int pop(){int size = que.size();size--;while(size--){que.push(que.front());que.pop();}int result = que.front();que.pop();return result;}int top(){return que.back();}bool empty(){return que.empty();}
};/*** Your MyStack object will be instantiated and called as such:* MyStack* obj = new MyStack();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->top();* bool param_4 = obj->empty();*/- 时间复杂度: pop为O(n),其他为O(1)
- 空间复杂度: O(n)
相关文章:

day10 用栈实现队列 用队列实现栈
题目1:232 用栈实现队列 题目链接:232 用栈实现队列 题意 用两个栈实现先入先出队列(一个入栈,一个出栈),实现如下功能: 1)push:将元素x推到队列末尾 2)…...
)
解决跨域问题(SpringBoot)
“什么是跨域?” 跨域 (Cross-Origin) 是指在浏览器的同源策略(Same-Origin Policy)下,一个网页的源(指协议、域名、端口号的组合)与另一个网页的源不同。因此,不同源的…...

LeetCode——2487. 从链表中移除节点
通过万岁!!! 题目:给你一个链表,然后让你从链表中移除一些节点,移除的规则就是我们选择的这个节点在原链表中往右不能有比这个节点大的值。思路:这个题我最开始以为是双指针,然后找…...

云原生和Kubernetes如何简化应用程序开发
在谈论当前技术时,“云计算”正变得非常普遍,作为开发人员,将会继续体验使用云计算应用程序的优势;在云计算中,另一个正在出现的术语是云原生。在进入实际话题之前,首先了解一下云原生到底是什么。 深入了解云原生应用 现在,世界各地的公司都了解云计算应用程序可以带来…...
)
点云从入门到精通技术详解100篇-基于深度学习的室内场景三维点云语义分割(续)
目录 CSegNet 语义分割模型构建 3.1 引言 3.2 偏移注意机制 3.3 网络主干 3.4 边缘卷积模块...

RabbitMQ消息可靠性保证机制3--消费端ACK机制
消费端ACK机制 在这之前已经完成了发送端的确认机制。可以保证数据成功的发送到RabbitMQ,以及持久化机制,然尔这依然无法完全保证整个过程的可靠性,因为如果消息被消费过程中业务处理失败了,但是消息却已经被标记为消费了&…...

Copilot在Pycharm的应用和示例
Copilot 是 Github 在 2021 年发布的 AI 代码助手工具,它可以根据你提供的上下文信息,自动生成代码建议,帮助提高代码编写效率和准确性。在 Pycharm 中使用 Copilot,可以进一步提升 Python 开发效率,本文将分享如何在 …...

搜维尔科技:【简报】第九届元宇宙数字人设计大赛,报名已经进入白热化阶段!
随着元宇宙时代的来临,数字人设计成为了创新前沿领域之一。为了提高大学生元宇宙虚拟人角色策划与美术设计的专业核心能力,我们特别举办了这场元宇宙数字人设计赛道,赛道主题为「AI人工智能科技」 ,只要与「AI人工智能科技」相关的…...
)
性能检测自动化(含内存泄露检测)
一、平台侧实现方案 1、UI case重复执行N次:进入页面,sleep 5s,记录start_time,sleep 30s,记录end_time,性能采集工具全程采集性能数据 2、根据采集到的性能数据,按照N次卡点性能数据:去掉最大的10%、最小的10%,求取平均值,作为单次性能数据结果f(n)…...

iec104和iec61850
iec104和iec61850 IEC104 规约详细解读(一) 协议结构 IEC104 规约详细解读(二)交互流程以及协议解析 61850开发知识总结与分享【1】 Get the necesarry projects next to each other in the same directory; $ git clone https://github.com/robidev/iec61850_open_server.g…...

redis 面试问题 (更新中 ing)
目录 reids 是做什么的为什么那么快有哪些使用场景redis有哪些 数据结构redis 有哪些底层数据结构为什么设计 sds一个 字符串 存储多大容量 stream为什么设计 streamstream 消费者消息丢失stream 消息私信问题 持久化机制redis 持久化机制,优缺点,怎么用…...
第389题找不同(Python))
力扣(leetcode)第389题找不同(Python)
389.找不同 题目链接:389.找不同 给定两个字符串 s 和 t ,它们只包含小写字母。 字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母。 请找出在 t 中被添加的字母。 示例 1: 输入:s “abcd”, t “abcde…...

Linux_源码编译安装LAMP
1. 安装httpd服务 在配置 Apache 网站服务之前,需要正确安装好 httpd 服务器软件。httpd 服务器的安装可以选用 RPM 安装、源码编译安装这两种方式,前者相对比较简单、快速,但是在功能上存在一定的局限性。在实际的生产环境中,使…...
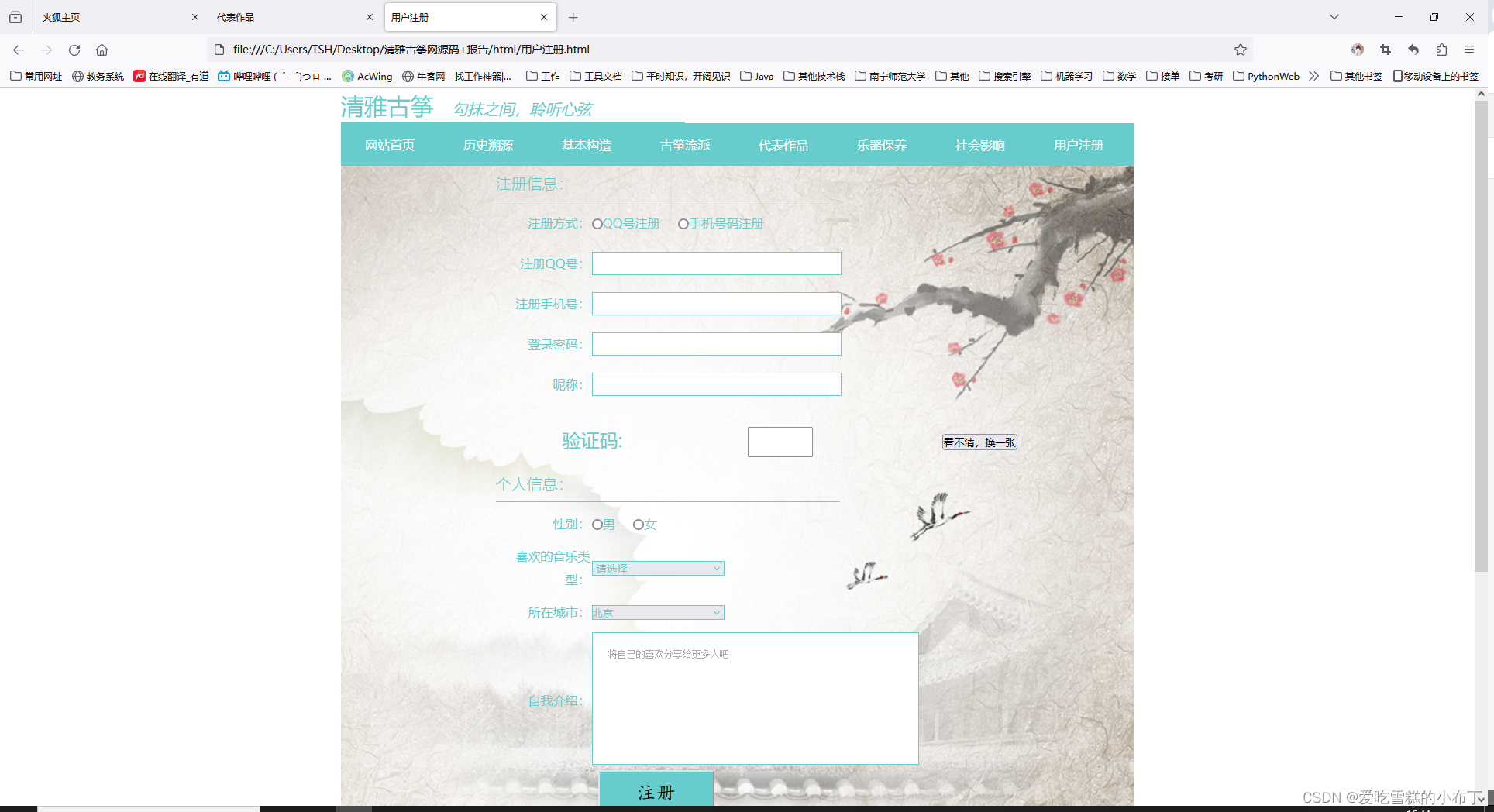
静态网页设计——清雅古筝网(HTML+CSS+JavaScript)
前言 声明:该文章只是做技术分享,若侵权请联系我删除。!! 感谢大佬的视频: https://www.bilibili.com/video/BV1T64y1K7Zn/?vd_source5f425e0074a7f92921f53ab87712357b 使用技术:HTMLCSSJS(…...
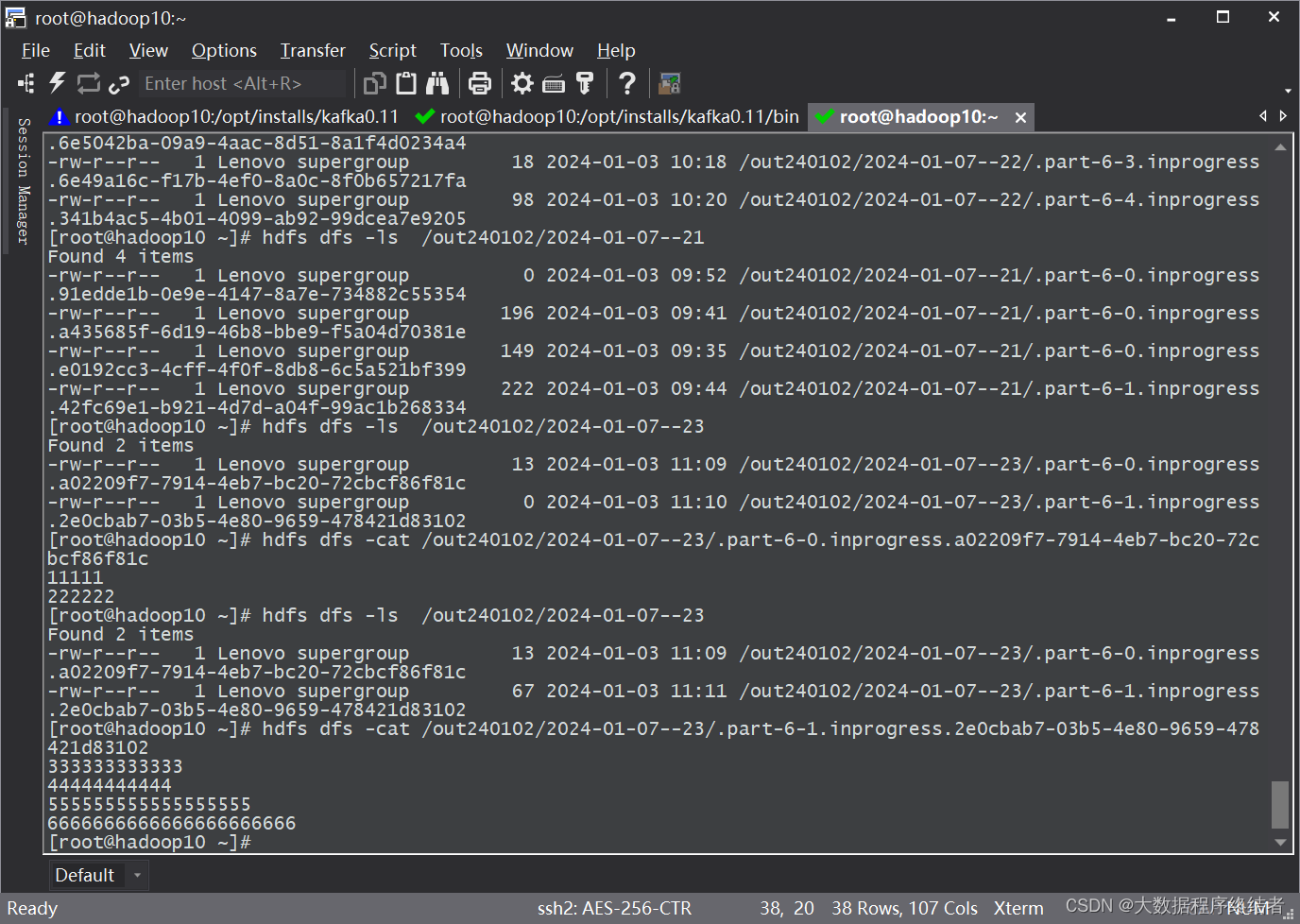
实战Flink Java api消费kafka实时数据落盘HDFS
文章目录 1 需求分析2 实验过程2.1 启动服务程序2.2 启动kafka生产 3 Java API 开发3.1 依赖3.2 代码部分 4 实验验证STEP1STEP2STEP3 5 时间窗口 1 需求分析 在Java api中,使用flink本地模式,消费kafka主题,并直接将数据存入hdfs中。 flin…...
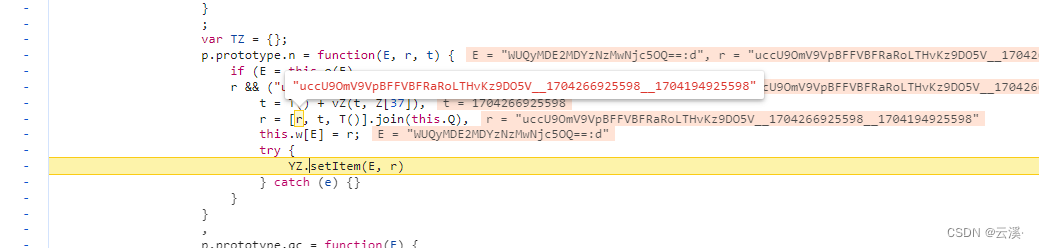
爬虫与反爬-localStorage指纹(某易某盾滑块指纹检测)(Hook案例)
概述:本文将用于了解爬虫中localStorage的检测原理以及讲述一个用于检测localStorage的反爬虫案例,最后对该参数进行Hook断点定位 目录: 一、LocalStorage 二、爬虫中localStorage的案例(以某盾滑块为例) 三、如何…...

聊一聊 webpack 和 vite 的开发服务代理的问题
webpack 和 vite webpackVite重新编辑的问题 changOrigin: true如何定义 /api ? webPack And Vite 都是两个比较好用的打包工具,尤其是 Vite, 几几年流行忘记了,特色就是服务启动极快,实现预加载,感觉 webPack 要比 Vite 要复杂一…...
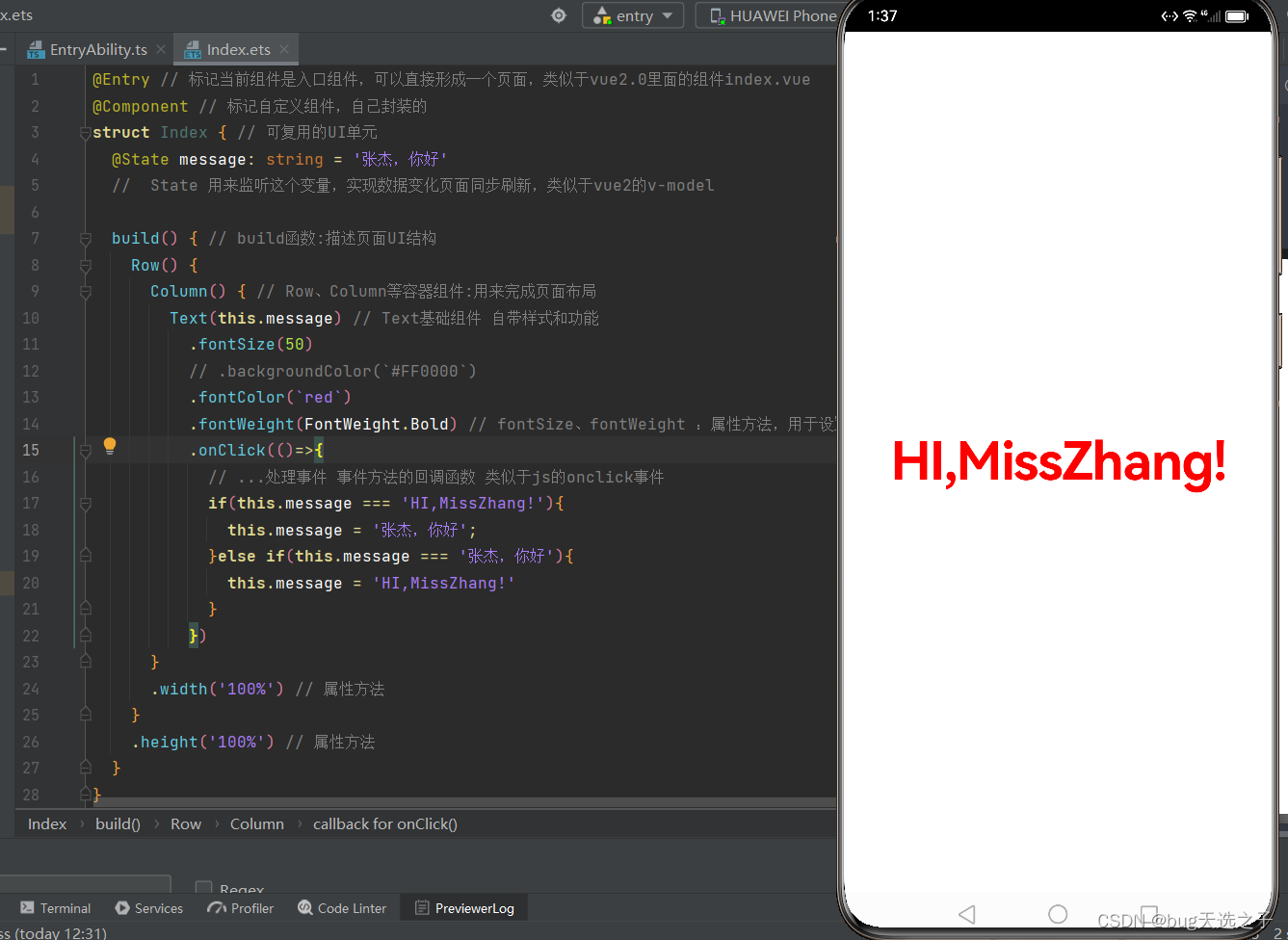
【鸿蒙4.0】安装DevEcoStudio
1.下载安装包 HUAWEI DevEco Studio和SDK下载和升级 | HarmonyOS开发者华为鸿蒙DevEco Studio是面向全场景的一站式集成开发环境,,在鸿蒙官网下载或升级操作系统开发工具DevEco Studio最新版本,SDK配置和下载,2.1支持Mac、Windows操作系统。…...

[概率论]四小时不挂猴博士
贝叶斯公式是什么 贝叶斯公式是概率论中的一个重要定理,用于计算在已知一些先验信息的情况下,更新对事件发生概率的估计。贝叶斯公式的表达式如下: P(A|B) P(B|A) * P(A) / P(B) 其中,P(A|B)表示在事件B发生的条件下事件A发生的概…...
算法通关村第二十关-黄金挑战图的常见算法
大家好我是苏麟 , 今天聊聊图的常见算法 . 图里的算法是很多的,这里我们介绍一些常见的图算法。这些算法一般都比较复杂,我们这里介绍这些算法的基本含义,适合面试的时候装*,如果手写,那就不用啦。 图分析算法…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
