金融中IC和IR的定义
当谈到金融领域时,IC(Information Coefficient)和IR(Information Ratio)通常是用来评估投资组合管理绩效的指标。它们都涉及到投资者对信息的利用和管理的效果。
信息系数(IC - Information Coefficient)
定义:信息系数是一种衡量投资组合经理或交易策略中,投资决策与实际市场表现之间关系的指标。
计算方法:IC的计算通常基于投资者的预测与实际结果之间的相关性。该系数的取值范围通常在-1到1之间,其中1表示完美的预测能力,-1表示完全相反的预测能力,0表示没有相关性。
应用:高IC值表明投资者的预测能力与市场表现高度相关,这通常被认为是投资者对信息的敏感度很高。较低的IC值可能表明投资者的预测能力不够准确或者市场效果太复杂,难以捕捉。

IC的计算方式有两种:normal IC、rank IC
因为normal IC有一个前提条件,就是数据要服从正态分布,现实往往不理想,所以实际中更多人采用rank IC(秩相关系数)来判断因子的有效性。两者分别对应Pearson 或者 Spearman 相关系数
信息比率(IR - Information Ratio)
IR指的是超额收益的均值与标准差之比。需要多个调仓期,每一个调仓期计算出一个IC值。
IR代表因子获得稳定Alpha的能力。 
相关文章:

金融中IC和IR的定义
当谈到金融领域时,IC(Information Coefficient)和IR(Information Ratio)通常是用来评估投资组合管理绩效的指标。它们都涉及到投资者对信息的利用和管理的效果。 信息系数(IC - Information Coefficient&a…...
Git(2):Git环境的安装
本教程里的git命令例子都是在Git Bash中演示的,会用到一些基本的linux命令,在此为大家提前列举: ls/ll 查看当前目录cat 查看文件内容touch 创建文件vi vi编辑器(使用vi编辑器是为了方便展示效果,学员可以记事本、edi…...

Pytest单元测试系列[v1.0.0][pytest插件常用技巧]
使用pytest-xdist并发执行测试 pytest-xdist:Run Tests in Parallel [https://pypi.python.org/pypi/pytest-xdist] 在自动化测试中有些资源只能同时被一个测试用例访问,如果不需要同时使用同一个资源,那么测试用例便可以并行执行 执行命令…...
嵌入式培训机构四个月实训课程笔记(完整版)-Linux系统编程第五天-Linux消息共享内存练习题(物联技术666)
更多配套资料CSDN地址:点赞+关注,功德无量。更多配套资料,欢迎私信。 物联技术666_嵌入式C语言开发,嵌入式硬件,嵌入式培训笔记-CSDN博客物联技术666擅长嵌入式C语言开发,嵌入式硬件,嵌入式培训笔记,等方面的知识,物联技术666关注机器学习,arm开发,物联网,嵌入式硬件,单片机…...
04set注入专题/简单类型/数组/List/Set/Map/空字符串/null/特殊符号
1.1注入外部Bean 在之前使用的案例就是注入外部Bean的方式。 <!-- class属性声明要管理哪个类中的对象 property标签的name是提示set方法名ref标签指明注入的bean的id--><bean id"userServiceBean" class"com.powernode.spring6.service.UserService…...

Linux引导和服务管理
目录 一.Linux引导: 1、Linux开机启动的完整过程: 2、bios的作用: 3、boot: 4.mbr: 5、grub: 6、加载内核文件: 7、启动进程: 8、centos6与centos7的区别: 9、完整的过程 …...
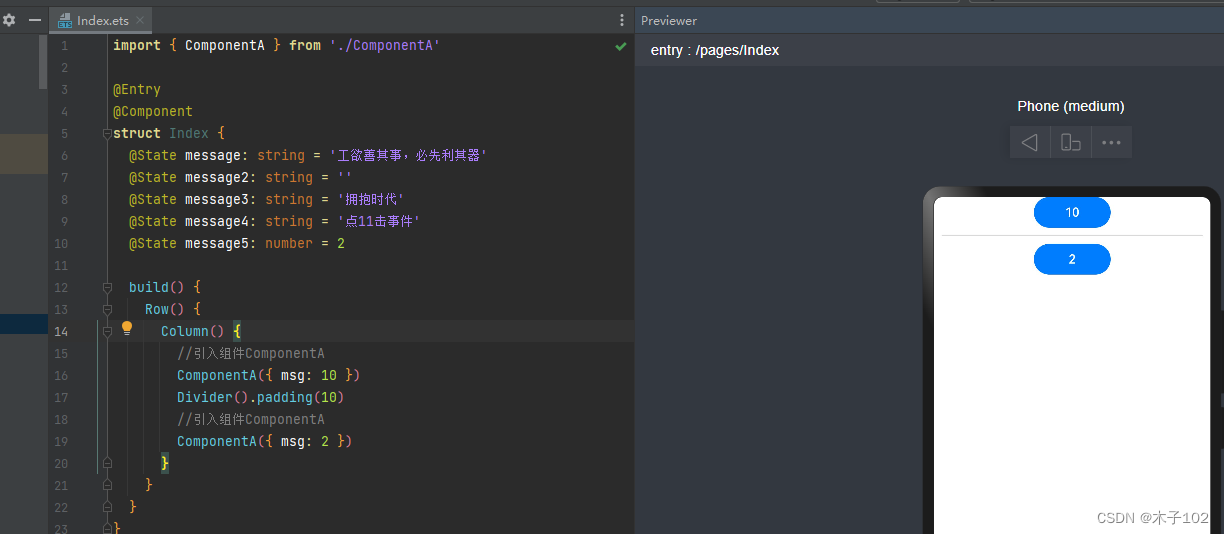
HarmonyOS 应用开发学习笔记 ets自定义组件及其引用 @Component自定义组件
Component注解的作用是用来构建自定义组件 Component组件官方文档 自定义组件具有以下特点: 可组合:允许开发者组合使用系统组件、及其属性和方法。 可重用:自定义组件可以被其他组件重用,并作为不同的实例在不同的父组件或容器…...
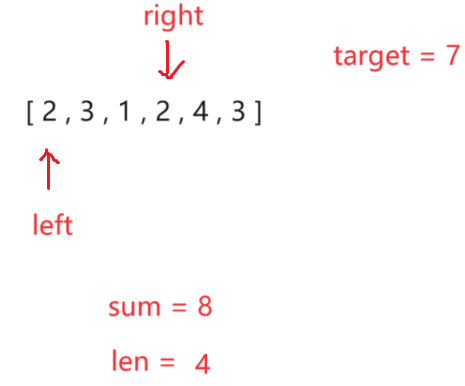
在做题中学习(43):长度最小的子数组
LCR 008. 长度最小的子数组 - 力扣(LeetCode) 解法:同向双指针-------滑动窗口算法 解释:本是暴力枚举做法,因为全部是正整数,就可以利用单调性和双指针解决问题来节省时间 思路: 如上面图&am…...
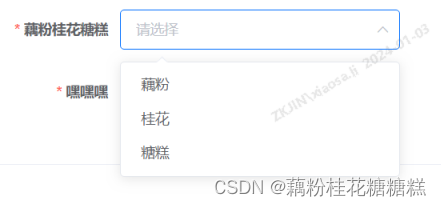
如何将 element-ui 中的 el-select 默认展开
<el-form-item label"藕粉桂花糖糕" prop"state" required><el-selectref"mySelect"v-model"form.state"style"width: 280px"placeholder"请选择"><el-option label"藕粉" :value"…...

Typora基本用法
文章目录 一、标题标题快捷键 二、段落1.换行2.分割线 三、文字显示1.字体2.上下标 四、列表1.无序列表2.有序列表3.任务列表 五、区块显示六、代码显示1.行内代码2.代码块 七、链接八、脚注九、图片插入十、表格十一、流程图十二、表情符号十三、数学公式的输入1.公式的插入①…...
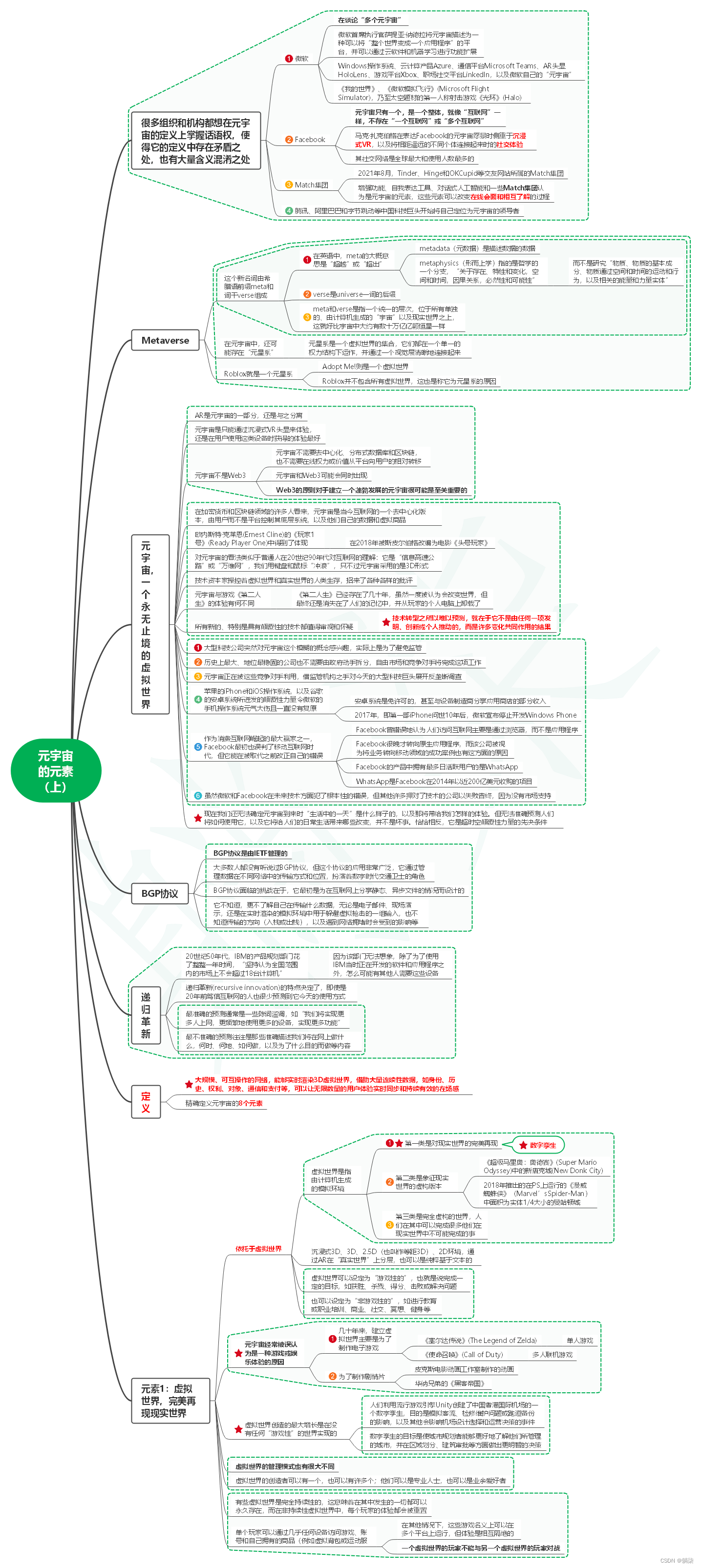
读元宇宙改变一切笔记02_元素(上)
1. 很多组织和机构都想在元宇宙的定义上掌握话语权,使得它的定义中存在矛盾之处,也有大量含义混淆之处 1.1. 微软 1.1.1. 在谈论“多个元宇宙” 1.1.2. 微软首席执行官萨提亚纳德拉将元宇宙描述为一种可以将“整个…...

听GPT 讲Rust源代码--compiler(2)
File: rust/compiler/rustc_codegen_cranelift/build_system/prepare.rs 在Rust源代码中,rust/compiler/rustc_codegen_cranelift/build_system/prepare.rs文件的作用是为Cranelift代码生成器构建系统准备依赖项。 具体来说,该文件的主要目标是处理Crane…...

SpringCloud系列篇:核心组件之负载均衡组件
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于SpringCloud的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.负载均衡组件是什么 二.负载均衡…...
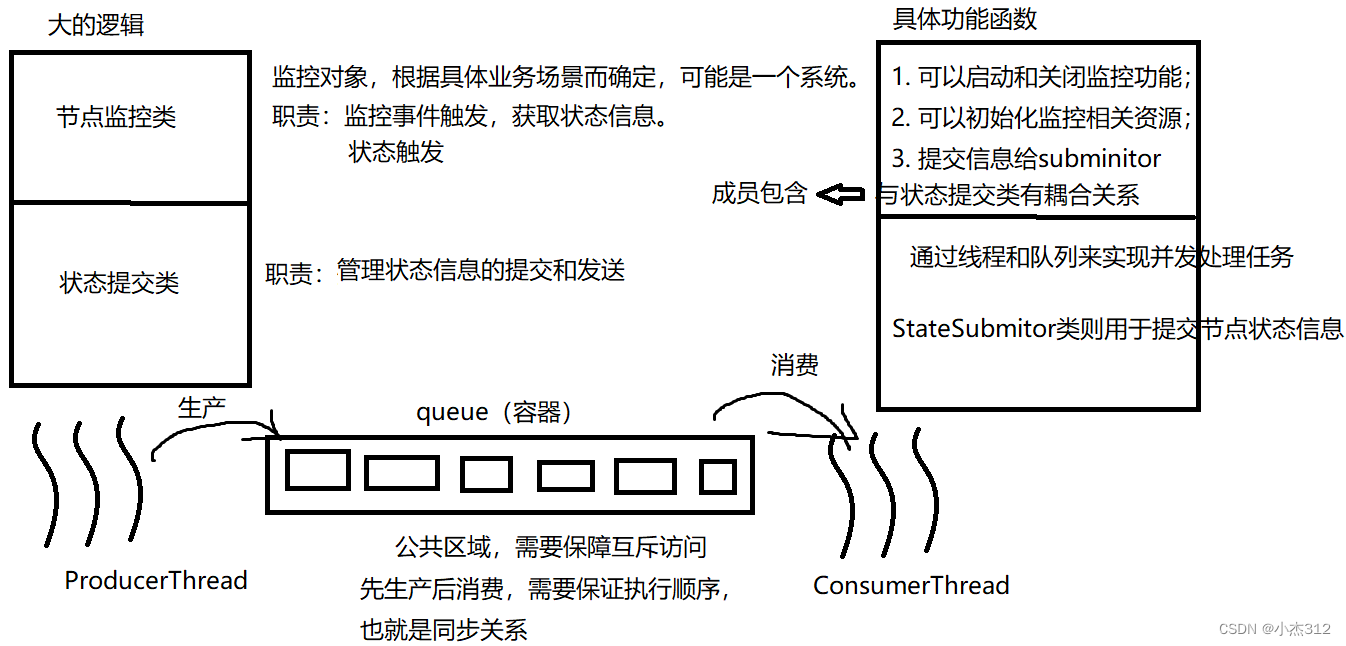
多线程模板应用实现(实践学习笔记)
出处:B站码出名企路 个人笔记:因为是跟着b站的教学视频以及文档初步学习,可能存在诸多的理解有误,对大家仅供借鉴,参考,然后是B站up阳哥的视频,我是跟着他学。大家有兴趣的可以到b站搜索。加油…...
)
Linux系统中MYSQL重置密码(针对root忘记密码)
⼀ .进⼊MySql配置⽂件中 vi /etc/my.cnf 在最后⼀⾏添加免密码登陆: skip-grant-tables :wq 保存退出 ⼆.重启MySql service mysql restart 或 systemctl restart mysqld.service 三. 登陆数据库 mysql -uroot -p 让输⼊密码直接回⻋就可以 四.修改MySql密码 use mysql…...

蓝桥杯基础知识1 字母大小写转换
蓝桥杯基础知识1 字母大小写转换 isalpha()判断一个字符是否为字母。 isalnum()判断一个字符是否为十进制数字字符或者字母,是否属于a~ z或A~ Z或0~9。 isdigit() 判断一个字符是否是十进制数字字符。十进制数字是:0 1 2 3 4 5 6 7 8 9 isalnum()和isdig…...
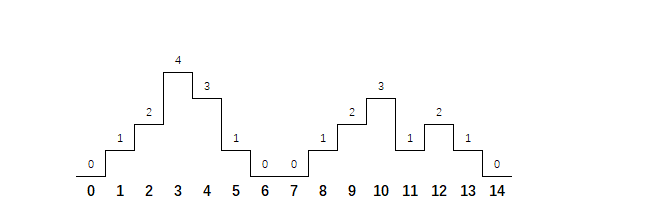
攀登者1 - 华为OD统一考试
OD统一考试 分值: 100分 题解: Java / Python / C++ 题目描述 攀登者喜欢寻找各种地图,并且尝试攀登到最高的山峰。 地图表示为一维数组,数组的索引代表水平位置,数组的元素代表相对海拔高度。其中数组元素0代表地面。 例如:[0,1,2,4,3,1,0,0,1,2,3,1,2,1,0],代表如下…...

通信原理期末复习——基础小题汇总(二)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:V…...

代码随想录刷题第四十二天| 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集
代码随想录刷题第四十二天 今天是0-1背包问题,掌握了套路就不难了~~~ 0-1背包问题理论基础(二维数组篇)卡码网第46题 题目思路: 代码实现: input_line input() # 读取一行输入 mn input_line.split() m, n int…...
前端开发加速器:十个VSCode插件精选
前端开发是一个不断发展的领域,随着技术的进步,工具也在不断更新。Visual Studio Code(VSCode)是前端开发者广泛使用的编辑器之一,得益于其强大的插件系统,可以帮助开发者提升工作效率。以下是十个对于前端…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
