代码随想录刷题第四十二天| 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集
代码随想录刷题第四十二天
今天是0-1背包问题,掌握了套路就不难了~~~
0-1背包问题理论基础(二维数组篇)卡码网第46题
题目思路:

代码实现:
input_line = input() # 读取一行输入
mn = input_line.split()
m, n = int(mn[0]), int(mn[1])
input_line = input().split()
weight = [int(input_str) for input_str in input_line]
input_line = input().split()
value = [int(input_str) for input_str in input_line]dp = [[0 for _ in range(n+1)] for _ in range(m)]if weight[0] <= n:for j in range(weight[0], n+1):dp[0][j] = value[0]for i in range(1, m):for j in range(1, n+1):if j < weight[i]:dp[i][j] = dp[i-1][j]else:dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])print(dp[m-1][n])
0-1背包问题理论基础(一维数组篇)卡码网第46题
题目思路:
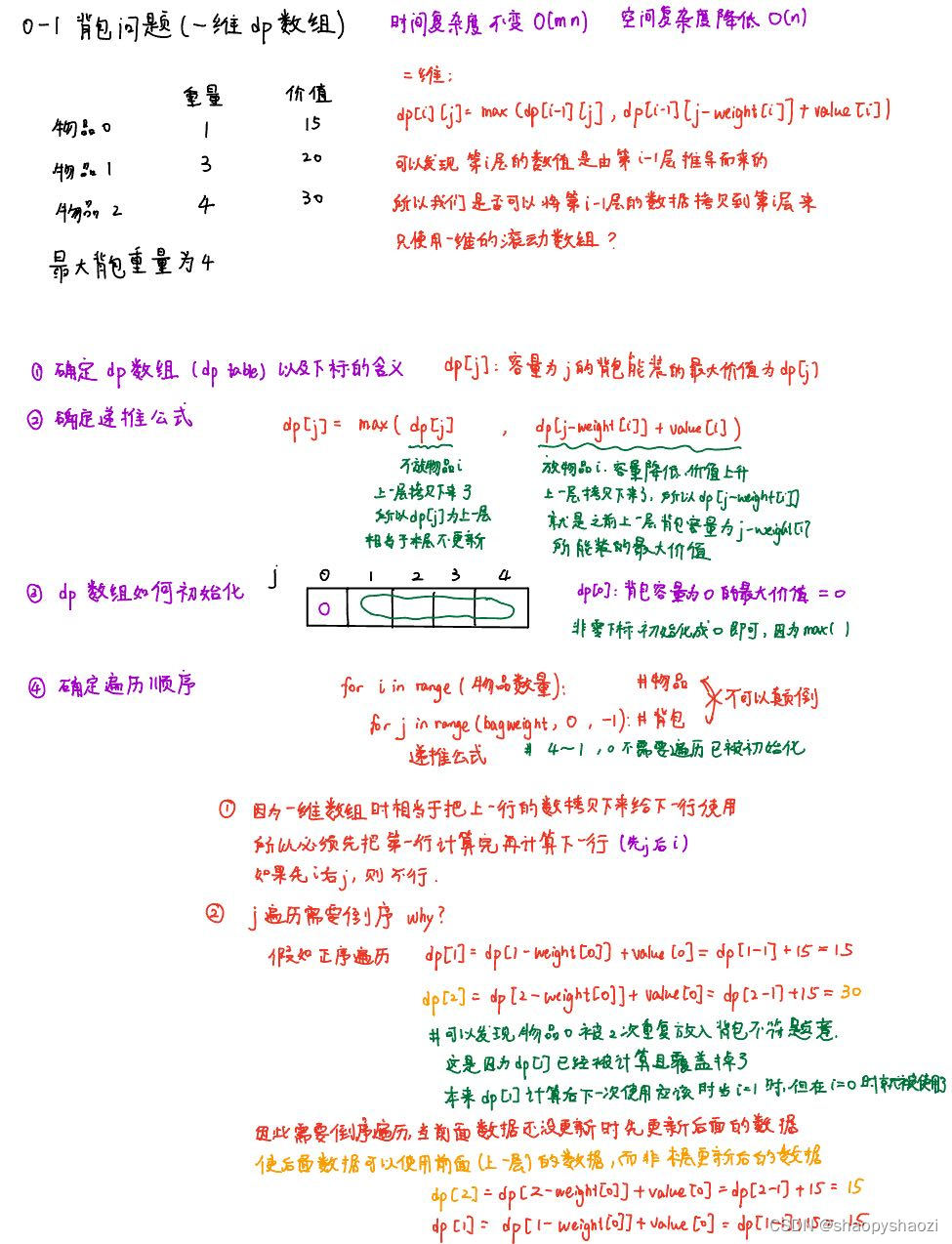
代码实现:
input_line = input() # 读取一行输入
mn = input_line.split()
m, n = int(mn[0]), int(mn[1])
input_line = input().split()
weight = [int(input_str) for input_str in input_line]
input_line = input().split()
value = [int(input_str) for input_str in input_line]dp = [0 for _ in range(n+1)]for i in range(m):for j in range(n, 0, -1):if j < weight[i]:dp[j] = dp[j]else:dp[j] = max(dp[j], dp[j-weight[i]]+value[i])print(dp[n])
分割等和子集 (LC 416)
题目思路:

代码实现:
class Solution:def canPartition(self, nums: List[int]) -> bool:allsum = sum(nums)if allsum%2 == 1:return Falsetarget = allsum//2dp = [[0 for _ in range(target+1)] for _ in range(len(nums))]if nums[0]<=target:for j in range(nums[0], target+1):dp[0][j] = nums[0]for i in range(1, len(nums)):for j in range(1, target+1):if nums[i] > j:dp[i][j] = dp[i-1][j]else:dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i])if dp[len(nums)-1][target] == target:return Trueelse:return False
相关文章:

代码随想录刷题第四十二天| 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集
代码随想录刷题第四十二天 今天是0-1背包问题,掌握了套路就不难了~~~ 0-1背包问题理论基础(二维数组篇)卡码网第46题 题目思路: 代码实现: input_line input() # 读取一行输入 mn input_line.split() m, n int…...
前端开发加速器:十个VSCode插件精选
前端开发是一个不断发展的领域,随着技术的进步,工具也在不断更新。Visual Studio Code(VSCode)是前端开发者广泛使用的编辑器之一,得益于其强大的插件系统,可以帮助开发者提升工作效率。以下是十个对于前端…...

剑指offer面试题3 二维数组中的查找
考察点: 考察数据结构二维数组知识点: 1.java中的数据类型分为基本类型和引用类型,数组属于引用类型,引用类型的变量中存储的是地址,该地址指向内存中的某个对象,参考c中的指针。2.一维数组定义,…...

【2023年中国高校大数据挑战赛 】赛题 B DNA 存储中的序列聚类与比对 Python实现
【2023年中国高校大数据挑战赛 】赛题 B DNA 存储中的序列聚类与比对 Python实现 更新时间:2023-12-29 1 题目 赛题 B DNA 存储中的序列聚类与比对 近年来,随着新互联网设备的大量涌入和对其服务需求的指数级增长,越来越多的数据信息被产…...
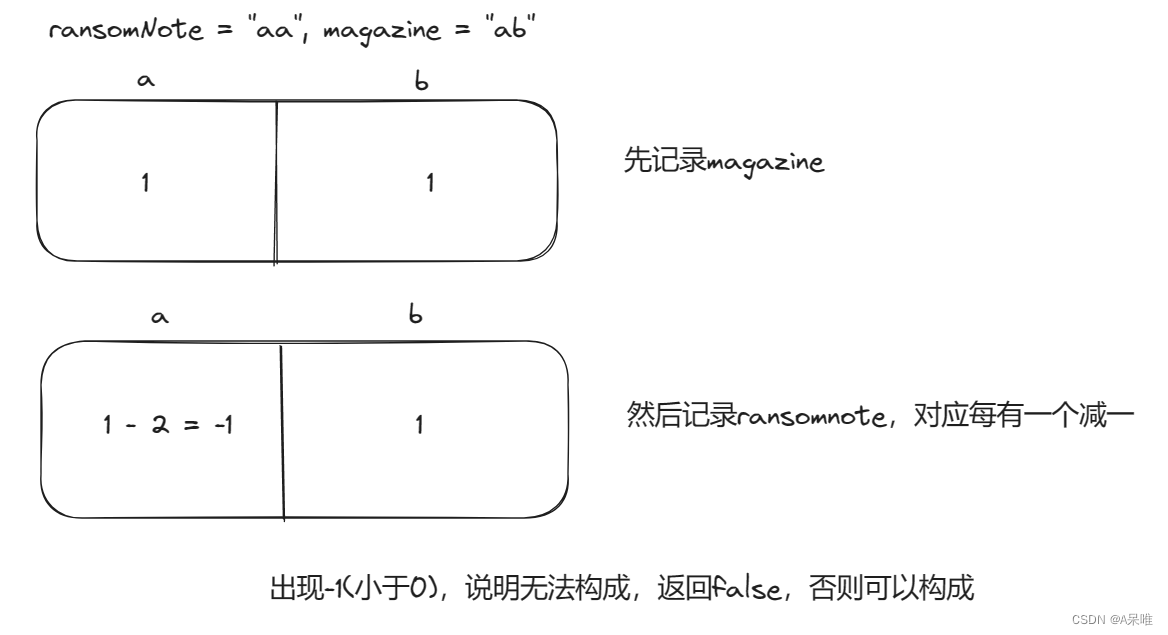
力扣383.赎金信 -- 哈希表
思路:记录magazine每个字符个数,然后记录ransomNote每个字符(每有一个减1),假如出现<0的情况说明ransomnode有字符的个数超过了magazine则无法构成,否则可以构成 代码: class Solution { pu…...
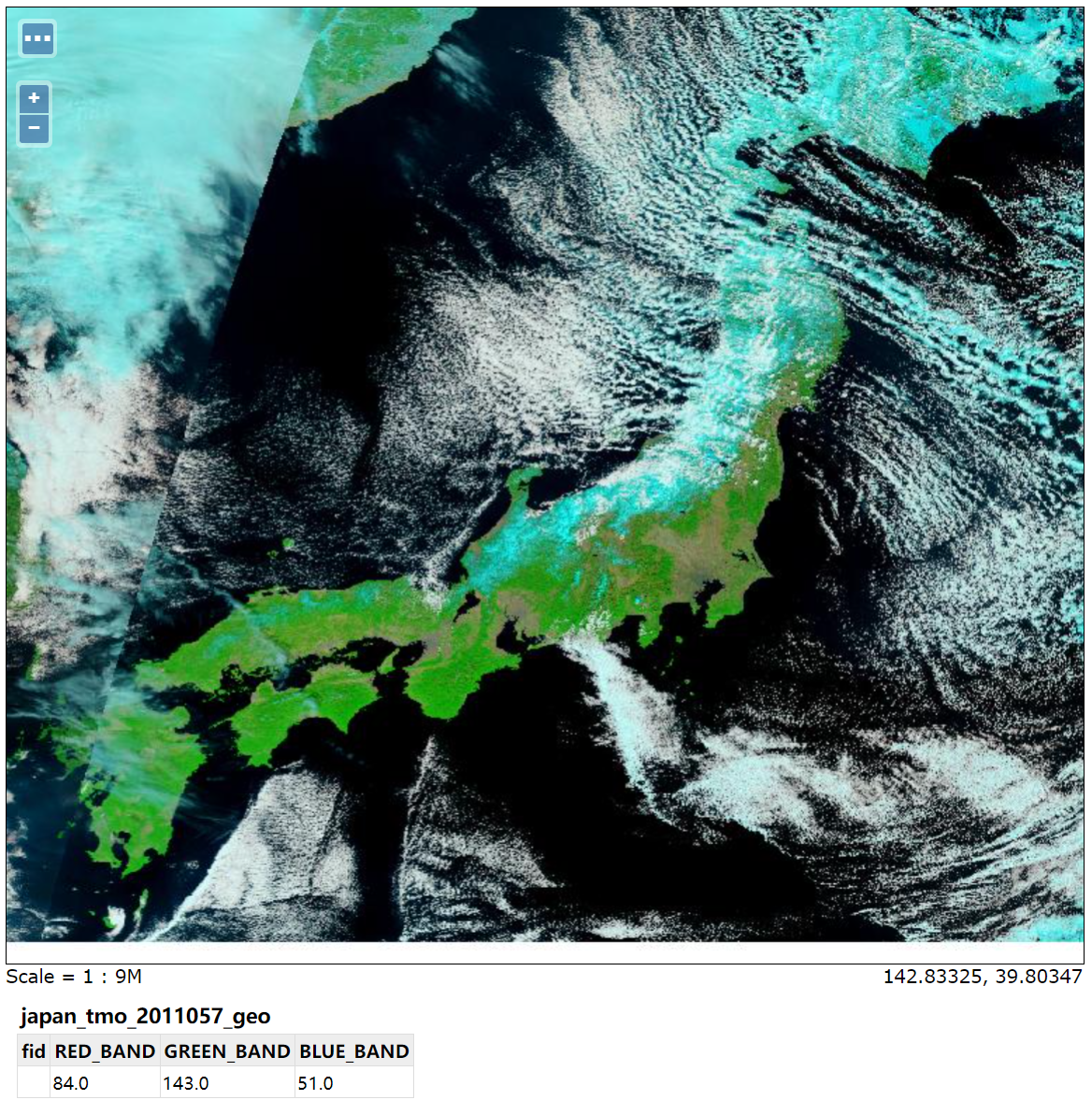
GeoServer发布地图服务(WMS、WFS)
文章目录 1. 概述2. 矢量数据源3. 栅格数据源 1. 概述 我们知道将GIS数据大致分成矢量数据和栅格数据(地形和三维模型都是兼具矢量和栅格数据的特性)。但是如果用来Web环境中,那么使用图片这个栅格形式的数据载体无疑是最为方便的࿰…...

C语言——结构体
一、结构体的创建 1、定义 在 C 语言中,结构体是一种自定义的数据类型,它允许将不同类型的数据项组合成一个单一实体。这在组织复杂数据时非常有用,因为它可以将有逻辑关系的数据组合在一起。结构体是一些值的集合,这些值是结构…...
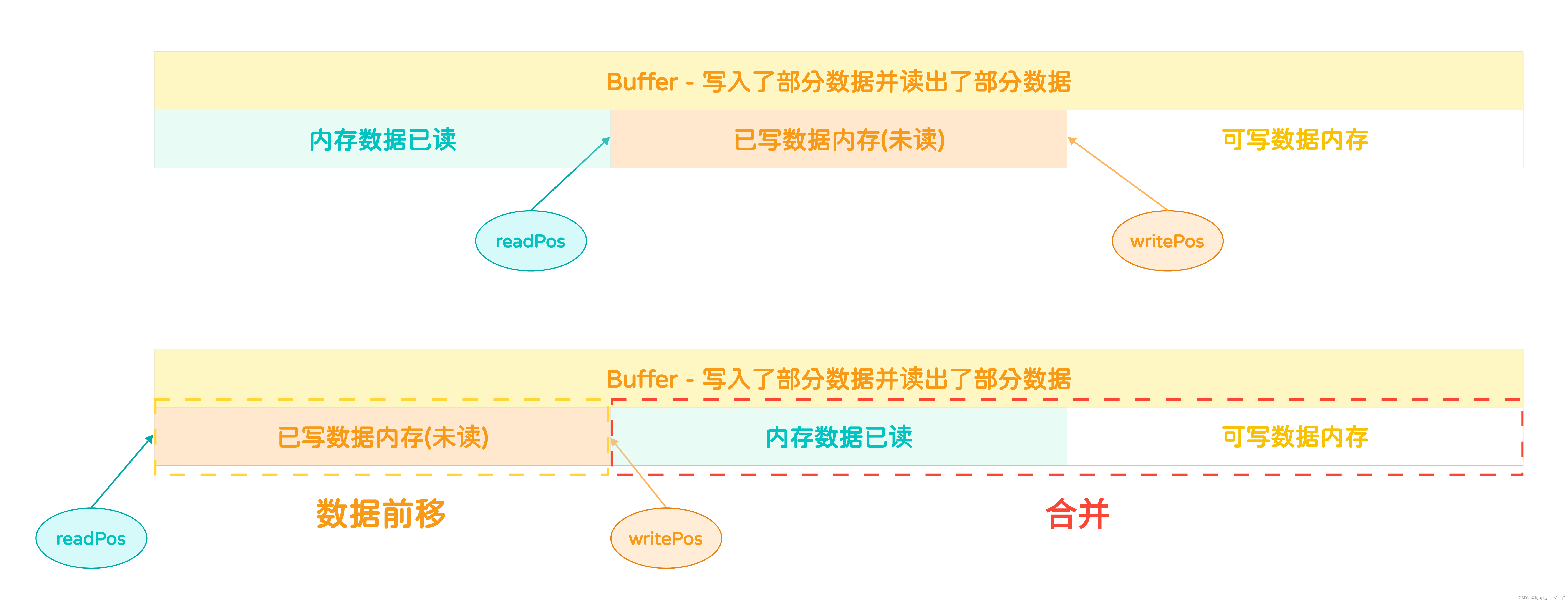
基于多反应堆的高并发服务器【C/C++/Reactor】(中)Buffer的创建和销毁、扩容、写入数据
TcpConnection:封装的就是建立连接之后得到的用于通信的文件描述符,然后基于这个文件描述符,在发送数据的时候,需要把数据先写入到一块内存里边,然后再把这块内存里边的数据发送给客户端,除了发送数据,剩下…...

【Linux】常用的基本命令指令①
前言:从今天开始,我们逐步的学习Linux中的内容,和一些网络的基本概念,各位一起努力呐! 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:数据结构 👈 💯代码…...

活动运营常用的ChatGPT通用提示词模板
活动目标确定:如何明确活动的目标,确保活动策划与执行的方向性? 活动主题选择:如何选择吸引人的活动主题,提高用户的参与度和兴趣? 活动形式策划:如何根据活动目标和主题,选择适合…...

SpringBoot 中实现订单30分钟自动取消的策略
简介 在电商和其他涉及到在线支付的应用中,通常需要实现一个功能:如果用户在生成订单后的一定时间内未完成支付,系统将自动取消该订单。 本文将详细介绍基于Spring Boot框架实现订单30分钟内未支付自动取消的几种方案,并提供实例…...

像专家一样使用TypeScript映射类型
掌握TypeScript的映射类型,了解TypeScript内置的实用类型是如何工作的。 您是否使用过Partial、Required、Readonly和Pick实用程序类型? 你知道他们内部是怎么运作的吗? 如果您想彻底掌握它们并创建自己的实用程序类型,那么不要错过本文所涵盖的内容。…...

Golang 结构体
前言 在 Go 语言中,结构体(struct)是一种自定义的数据类型,将多个不同类型的字段(fields)组合在一起 结构体通常用于模拟真实世界对象的属性和行为 定义结构体 可以使用 type 关键字和 struct 关键字来定…...

服务器运行状况监控工具
服务器运行状况监视提供了每个服务器状态和性能的广泛概述,通过监控服务器指标,如 CPU 使用率、内存消耗、I/O、磁盘使用率、进程等,服务器运行状况监控可以避免服务器停机。 服务器性能监控指标 服务器是网络中最重要的组件之一࿰…...
)
2022年全国职业院校技能大赛软件测试赛题卷②—自动化测试解析报告(含术语)
2022年全国职业院校技能大赛软件测试任务四 自动化测试 目录 第一题:按照以下步骤在PyCharm中进行自动化测试脚本编写,并执行脚本。...

497 蓝桥杯 成绩分析 简单
497 蓝桥杯 成绩分析 简单 //C风格解法1,*max_element()与*min_element()求最值 //时间复杂度O(n),通过率100% #include <bits/stdc.h> using namespace std;using ll long long; const int N 1e4 …...
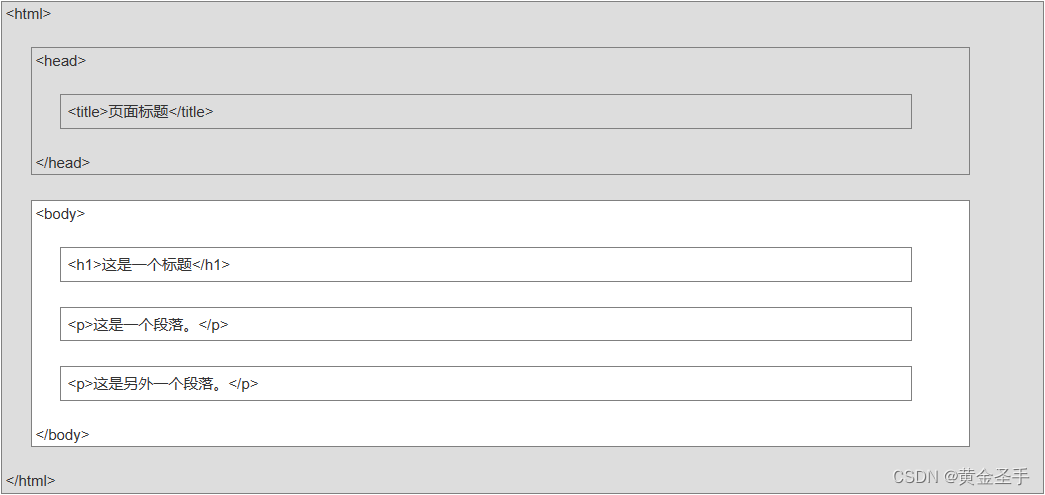
一、HTML5简介
一、简介 超文本标记语言(英语:HyperText Markup Language,简称:HTML)是一种用于创建网页的标准标记语言。可以使用 HTML 来建立自己的 WEB 站点,HTML 运行在浏览器上,由浏览器来解析。 <!…...
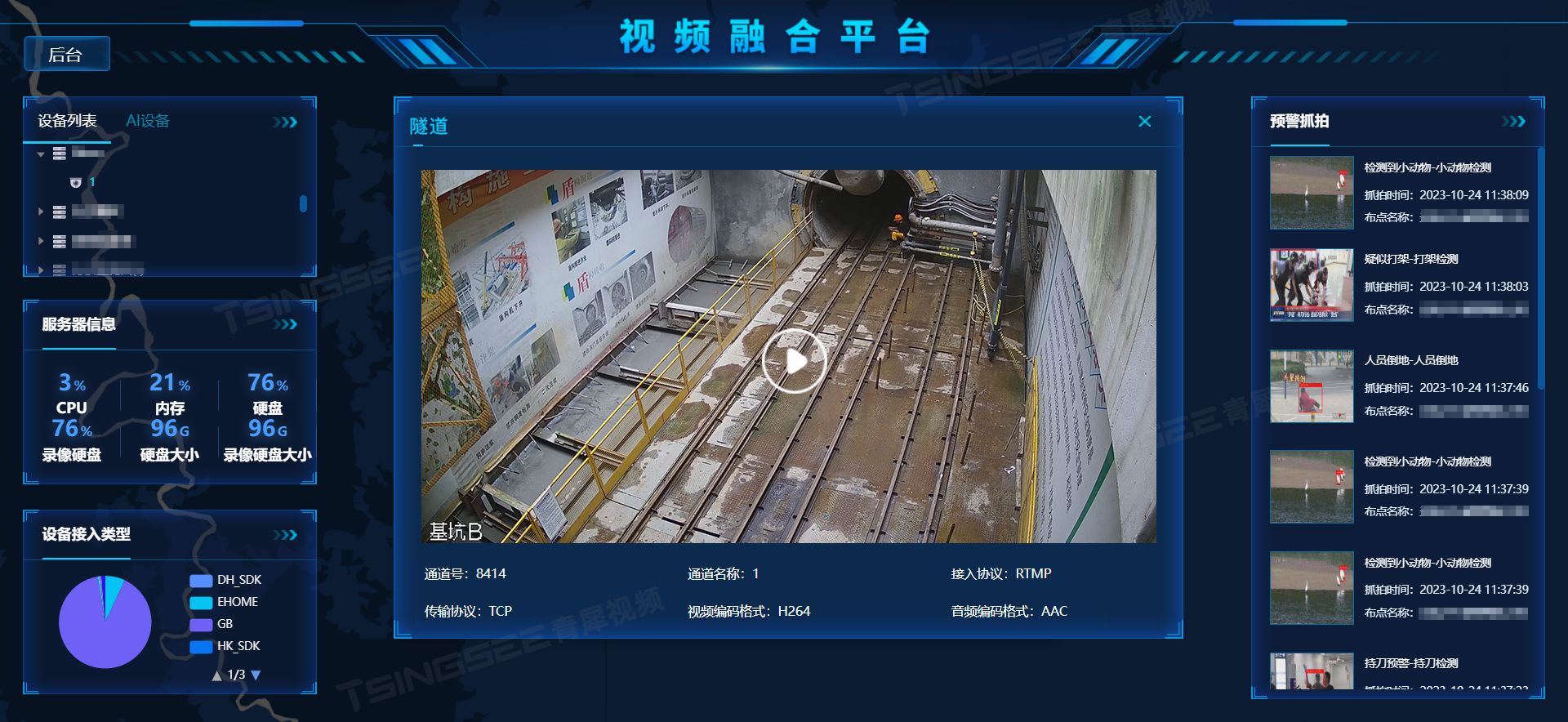
视频云存储/视频智能分析平台EasyCVR在麒麟系统中无法启动该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
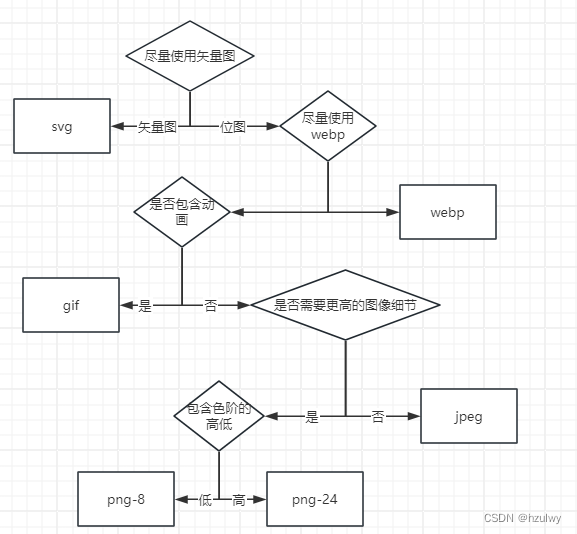
前端性能优化之图像优化
图像优化问题主要可以分为两方面:图像的选取和使用,图像的加载和显示。 图像基础 HTTP Archive上的数据显示,网站传输的数据中,60%的资源都是由各种图像文件组成的,当然这些是将各类型网站平均的结果,单独…...
微信小程序封装vant 下拉框select 单选组件
先上效果图: 主要是用vant 小程序组件封装的:vant 小程序ui网址:vant-weapp 主要代码如下: 先封装子组件: select-popup 放在 components 文件夹里面 select-popup.wxml: <!--pages/select-popup/select-popup.wxml--> &…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
