497 蓝桥杯 成绩分析 简单
497 蓝桥杯 成绩分析 简单


//C++风格解法1,*max_element()与*min_element()求最值
//时间复杂度O(n),通过率100%
#include <bits/stdc++.h>
using namespace std;using ll = long long;
const int N = 1e4 + 10;
int a[N];int main(){ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n;cin >> n;for(int i = 1; i <= n; ++i)cin >> a[i];cout << *max_element(a + 1, a + 1 + n) << '\n';cout << *min_element(a + 1, a + 1 + n) << '\n';ll sum = 0;for(int i = 1; i <= n; ++i)sum += a[i];cout << fixed << setprecision(2) << 1.0 * sum / n <<'\n';return 0;
}*max_element()与*min_element()分别用来求最大元素和最小元素的值,
如果不加 * 获取的是地址。
虽然集合作为二叉树实现, 但是时间复杂度O(n),n为数组大小(由传入的参数决定)
在集合或其他有序容器上使用相同的比较函数,函数是线性的,触及每个元素,因为在恒定时间内使用.rbegin()。
如果使用不同的比较函数,则无法保证顺序一致,但同样必须触及每个元素,并且至少是线性的。
接收参数:容器的首尾地址(迭代器)(可以是一个区间)
返回:最值元素的值
C++ primer (中文版第四版)第273页
9.3.2 begin和end成员
begin和end操作产生指向容器内第一个元素和最后一个元素的下一个位置的迭代器,
如下所示。这两个迭代器通常用于标记包含容器中所有元素的迭代范围。
c.begin() 返回一个迭代器,它指向容器c的第一个元素
c.end() 返回一个迭代器,它指向容器c的最后一个元素的下一个位置
c.rbegin() 返回一个逆序迭代器,它指向容器c的最后一个元素
c.rend() 返回一个逆序迭代器,它指向容器c的第一个元素前面的位置
上述每个操作都有两个不同的版本:一个是const成员,另一个是非const成员。这些操作返回什么类型取决于容器是否为const。如果容器不是const,则这些操作返回iterator或reverse_iterator类型。如果容器是const,则其返回类型要加上const_前缀,也就是const_iterator和const_reverse_iterator类型。
begin();end()正序迭代器cbegin();cend()返回const的begin();end()rbegin();rend()逆序迭代器crbegin();crend()返回const的rbegin();rend()
用fixed,一个manipulator,消除浮点数的科学计数法。
只要出现了fixed,后面都按fixed输出。
fixed与setprecision(n)连用可以控制小数点后的位数,可以理解为定点数记数法。
没有fixed,就是浮点数记数法,控制的就是有效数字的位数(包括小数点前的)
fixed是一个计算机专业术语,指向托管变量的指针并在 statement 执行期间“钉住”该变量。
fixed流操作符,它表示浮点输出应该以固定点或小数点表示法显示。
//C++风格解法2,打擂台算法,max()、min()通过率100%
#include <bits/stdc++.h>
using namespace std;const int N = 1e4 + 10;
int a[N];int main(){ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n;cin >> n;for(int i = 1; i <= n; ++i)cin >> a[i];int mx = a[1], mi = a[1];for(int i = 1; i <= n ; ++i){mx = max(mx, a[i]);mi = min(mi, a[i]);}cout << mx << '\n' << mi << '\n';int sum = 0;for(int i = 1; i <= n; ++i)sum += a[i];cout << fixed << setprecision(2) << 1.0 * sum / n <<'\n';//1.0 * sum / n 强制转化为浮点数return 0;
}min(a,b)返回a和b中较小的那个值,只能传入两个值,或传入一个列表。
min(1,2) = 1
min({1,2,3,4}) = 1
同理可得max(a,b)的含义和表示,时间复杂度为O(1),传入参数为数组时时间复杂度为O(n),
n为数组大小。
C/C++中“/”本身带有取整的含义,n*1/i,即意味着整数除以整数,结果取整;n*1.0/i即意味着浮点数除以整数,结果会强制转换为浮点数。
//C风格解法3,打擂台算法,通过率100%
#include <stdio.h>
#include <stdlib.h>int main(){int n,i,a[10001];float aver = 0;int max = 0,min = 100;scanf("%d", &n);for(i = 0; i < n; i++){scanf("%d", &a[i]);aver += a[i];if(a[i] > max)max = a[i];if(a[i] < min)min = a[i];}aver = aver / n;printf("%d\n %d\n %.2f",max,min,aver);return 0;
}在C语言中,printf() 函数中的 %5.2f 是一个格式说明符,用于格式化浮点数的输出。
-
%:格式说明符的起始标志。
-
5:字段宽度,表示输出的最小字符数,包括空格(可能没有)、整数部分、小数点和小数部分。它指定了输出的总宽度为5个字符。
-
.:小数点用来分隔整数部分和小数部分。
-
2:精度,表示小数部分的位数。指定小数部分保留2位。
-
f:表示要格式化的数据类型是浮点数。
-
浮点数 3.14159 并使用 %5.2f 进行格式化输出,它将输出为 "空格3.14",总共占据5个字符的宽度,其中有一个空格字符,一个整数,一个小数点字符和两个小数。而且没有负号,所以在左侧输出一个空格占位,即右对齐输出。
-
浮点数3.5,使用%-5.2f进行格式化输出,那么就是输出"3.50空格",3.50总共有4位,总共占据5个字符的宽度,而且有负号,所以在右侧输出一个空格占位,即左对齐输出。
-
没有负号右对齐,位数不足,左边补齐空格,满足或超过位数,原样输出。
-
有负号左对齐,位数不足,右边补空格。
-
printf("%-4d",20); 输出"20空格空格"(左对齐,右边补2个空格),printf("%-4d",12345); 输出:12345(原样输出)
-
printf("%4d",20); 输出"空格空格20"(右对齐,左边补2个空格),printf("%2d",12345); 输出:12345(原样输出)
reference:
C++max_element()min_element()函数简介 - 知乎 (zhihu.com)
C++ max_element()的使用-CSDN博客
c++ - STL max_element 的复杂度 - IT工具网 (coder.work)
反向迭代器(rbegin,rend)-CSDN博客
C++ 容器中 begin()、cbegin()、rbegin()、crbegin-CSDN博客
详解C++中fixed,setprecision(),setw()的用法_c++ fixed-CSDN博客
如何深刻理解IEEE浮点数的表示(IEEE floating-point representation)_ieee floating point-CSDN博客
C++003-C++变量和数据类型2_c++输入正方形的边长m和n,计算阴影部分的面积-CSDN博客
C语言基础;打擂台算法_打擂台算法流程图-CSDN博客
sum=sum+n*1.0/i;与 sum=sum+n*1/i;为什么输出结果不一样? - 知乎 (zhihu.com)
C语言中printf输出特殊字符(“%d“或者“\n“)_c语言中d%\n是什么意思-CSDN博客
在C语言中,printf("max is %d\n",max)和printf("%d",max)有区别吗?_百度知道 (baidu.com)
C语言中输出格式%.2f和%1.2f有什么不同? - 知乎 (zhihu.com)
c语言printf()函数中的%5.2f是什么意思?_百度知道 (baidu.com)
相关文章:

497 蓝桥杯 成绩分析 简单
497 蓝桥杯 成绩分析 简单 //C风格解法1,*max_element()与*min_element()求最值 //时间复杂度O(n),通过率100% #include <bits/stdc.h> using namespace std;using ll long long; const int N 1e4 …...
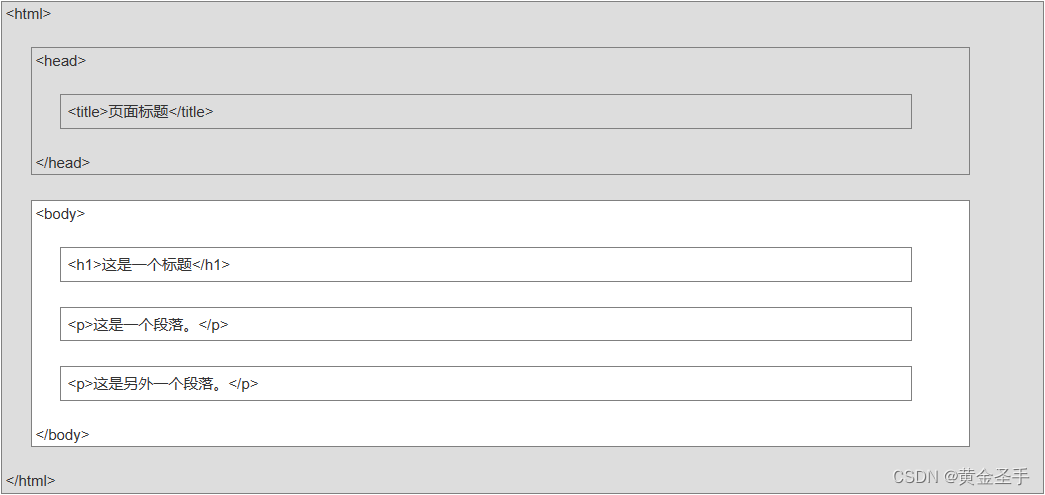
一、HTML5简介
一、简介 超文本标记语言(英语:HyperText Markup Language,简称:HTML)是一种用于创建网页的标准标记语言。可以使用 HTML 来建立自己的 WEB 站点,HTML 运行在浏览器上,由浏览器来解析。 <!…...
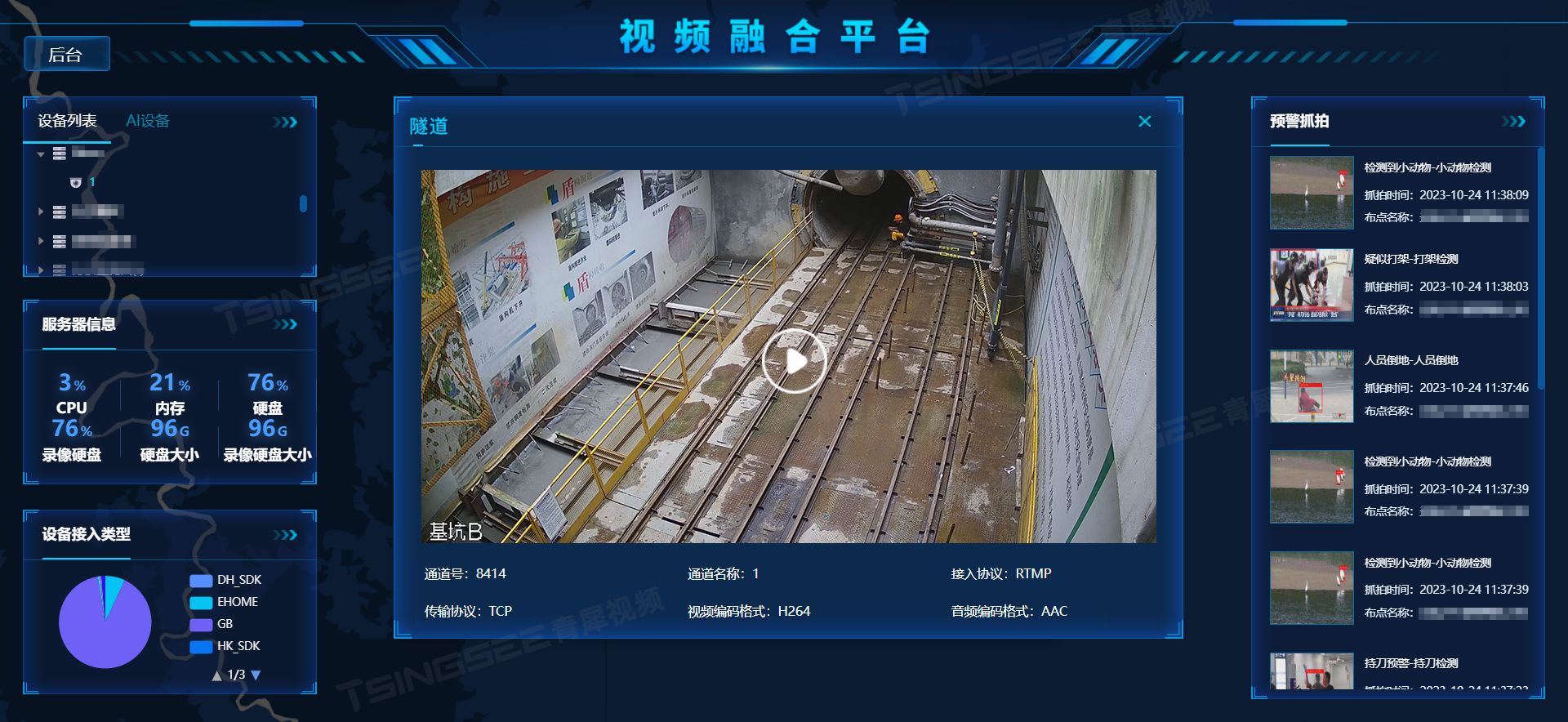
视频云存储/视频智能分析平台EasyCVR在麒麟系统中无法启动该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
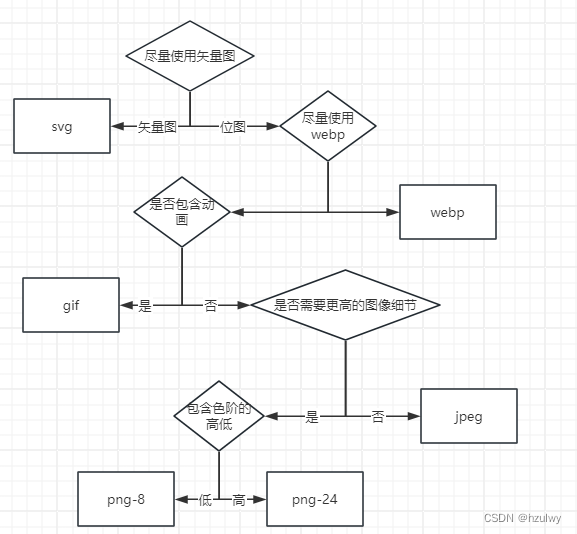
前端性能优化之图像优化
图像优化问题主要可以分为两方面:图像的选取和使用,图像的加载和显示。 图像基础 HTTP Archive上的数据显示,网站传输的数据中,60%的资源都是由各种图像文件组成的,当然这些是将各类型网站平均的结果,单独…...
微信小程序封装vant 下拉框select 单选组件
先上效果图: 主要是用vant 小程序组件封装的:vant 小程序ui网址:vant-weapp 主要代码如下: 先封装子组件: select-popup 放在 components 文件夹里面 select-popup.wxml: <!--pages/select-popup/select-popup.wxml--> &…...

c语言试卷
江西财经大学IT帮 2020-2021第一学期期末C语言模拟考试试卷 课程名称:C语言程序设计(软件)(主干课程) 适用对象:21级本科 试卷命题人 钟芳盛 游天悦 李俊贤 万军豪 张位 试卷审核人 钟芳盛 一、单项…...

文献阅读:Sparse Low-rank Adaptation of Pre-trained Language Models
文献阅读:Sparse Low-rank Adaptation of Pre-trained Language Models 1. 文章简介2. 具体方法介绍 1. SoRA具体结构2. 阈值选取考察 3. 实验 & 结论 1. 基础实验 1. 实验设置2. 结果分析 2. 细节讨论 1. 稀疏度分析2. rank分析3. 参数位置分析4. 效率考察 4.…...
NCC基础开发技能培训
YonBuilder for NCC 是一个带插件的eclipse工具,跟eclipse没什么区别 NC Cloud2021.11版本开发环境搭建改动 https://nccdev.yonyou.com/article/detail/495 不管是NC Cloud 新手还是老NC开发,在开发NC Cloud时开发环境搭建必看!ÿ…...
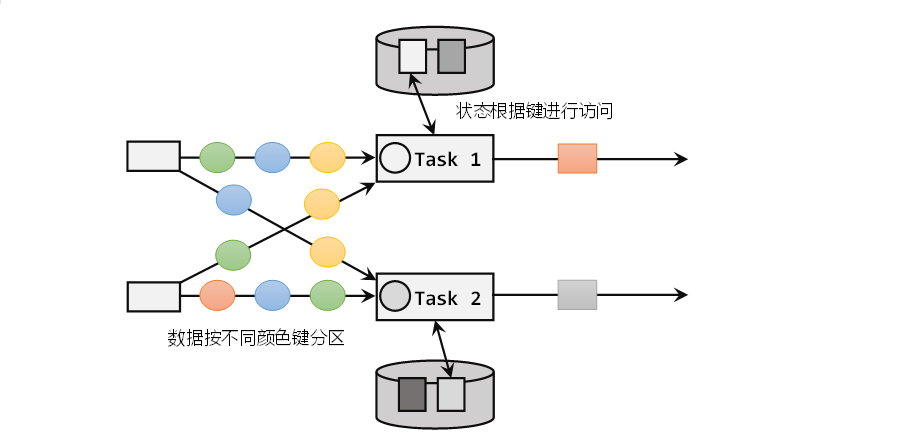
Flink中的状态管理
一.Flink中的状态 1.1 概述 在Flink中,算子任务可以分为有状态和无状态两种状态。 无状态的算子任务只需要观察每个独立事件,根据当前输入的数据直接转换输出结果。例如Map、Filter、FlatMap都是属于无状态算子。 而有状态的算子任务,就…...

【linux】线程互斥
线程互斥 1.线程互斥2.可重入VS线程安全3.常见锁的概念 喜欢的点赞,收藏,关注一下把! 1.线程互斥 到目前为止我们学了线程概念,线程控制接下来我们进行下一个话题,线程互斥。 有没有考虑过这样的一个问题,…...

机器学习原理到Python代码实现之LinearRegression
Linear Regression 线性回归模型 该文章作为机器学习的第一篇文章,主要介绍线性回归模型的原理和实现方法。 更多相关工作请参考:Github 算法介绍 线性回归模型是一种常见的机器学习模型,用于预测一个连续的目标变量(也称为响应变…...

Hive SQL / SQL
1. 建表 & 拉取表2. 插入数据 insert select3. 查询3.1 查询语句语法/顺序3.2 关系操作符3.3 聚合函数3.4 where3.5 分组聚合3.6 having 筛选分组后结果3.7 显式类型转换 & select产生指定值的列 4. join 横向拼接4.1 等值连接 & 不等值连接4.2 两表连接4.2.1 内连…...

程序媛的mac修炼手册--MacOS系统更新升级史
啊,我这个口罩三年从未感染过新冠的天选免疫王,却被支原体击倒😷大意了,前几天去医院体检,刚检查完出医院就摘口罩了🤦大伙儿还是要注意戴口罩,保重身体啊!身体欠恙,就闲…...

【数据库原理】(9)SQL简介
一.SQL 的发展历史 起源:SQL 起源于 1970 年代,由 IBM 的研究员 Edgar F. Codd 提出的关系模型概念演化而来。初期:Boyce 和 Chamberlin 在 IBM 开发了 SQUARE 语言的原型,后发展成为 SQL。这是为了更好地利用和管理关系数据库。…...

第二百五十二回
文章目录 概念介绍实现方法示例代码 我们在上一章回中介绍了如何在页面中添加图片相关的内容,本章回中将介绍如何给组件添加阴影.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在本章回中介绍的阴影类似影子,只是它不像影子那么明显&a…...
)
Leetcode 3701 · Find Nearest Right Node in Binary Tree (遍历和BFS好题)
3701 Find Nearest Right Node in Binary TreePRE Algorithms This topic is a pre-release topic. If you encounter any problems, please contact us via “Problem Correction”, and we will upgrade your account to VIP as a thank you. Description Given a binary t…...

网站被攻击了,接入CDN对比直接使用高防服务器有哪些优势
网站是互联网行业中经常被攻击的目标之一。攻击是许多站长最害怕遇到的情况。当用户访问一个网站,页面半天打不开,响应缓慢,或者直接打不开,多半是会直接走开,而不是等待继续等待相应。针对网站攻击的防护,…...

location常用属性和方法
目录 Location 对象 Location 对象属性 Location 对象方法 location.assign() location.replace() location.reload() Location 对象 Location 对象包含有关当前 URL 的信息。Location 对象是 Window 对象的一个部分,可通过 window.location 属性来访问。 L…...

二分图
目录 二分图 染色法判定二分图 匈牙利算法 二分图 二分图,又叫二部图,将所有点分成两个集合,使得所有边只出现在集合之间的点之间,而集合内部的点之间没有边。二分图当且仅当图中没有奇数环。只要图中环的边数没奇数个数的&am…...
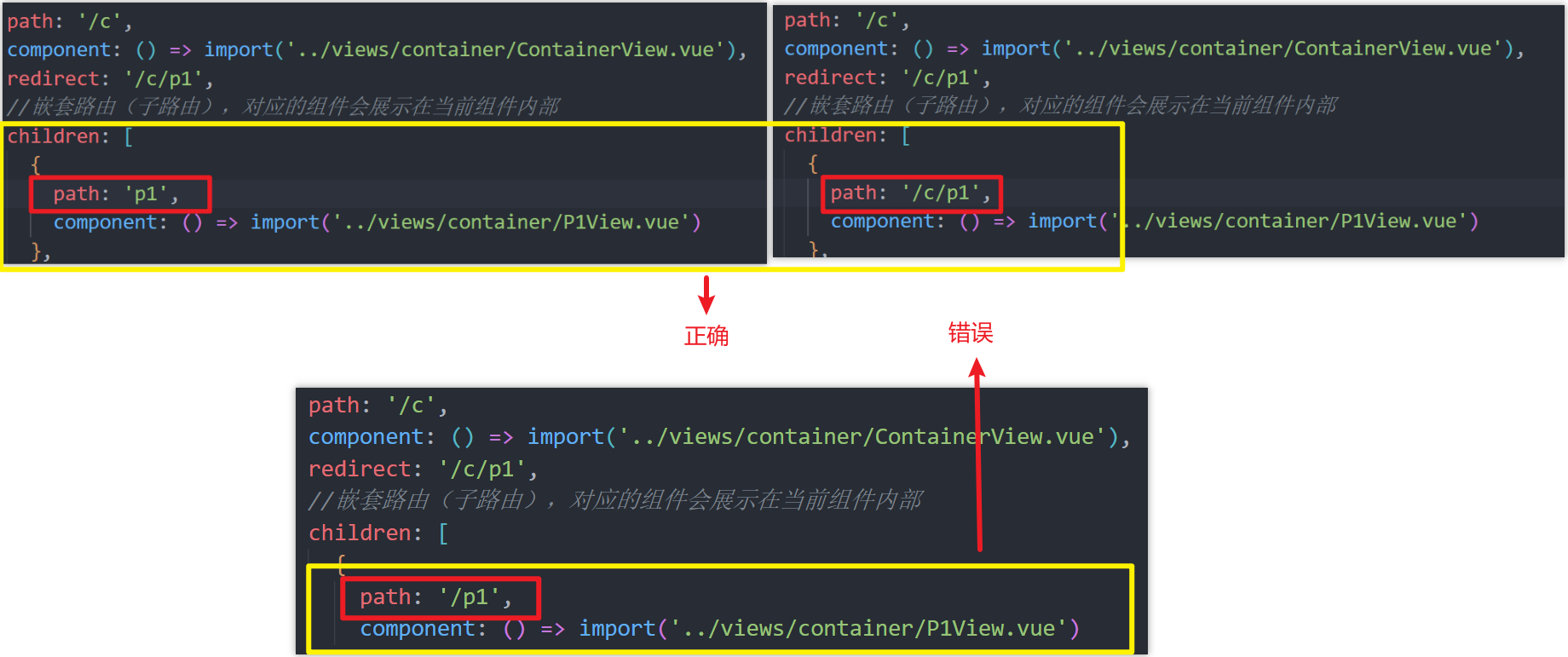
[VUE]3-路由
目录 路由 Vue-Router1、Vue-Router 介绍2、路由配置3、嵌套路由3.1、简介3.2、实现步骤3.3、⭐注意事项 4、⭐router-view标签详解 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
