二分图
目录
二分图
染色法判定二分图
匈牙利算法
二分图
- 二分图,又叫二部图,将所有点分成两个集合,使得所有边只出现在集合之间的点之间,而集合内部的点之间没有边。
- 二分图当且仅当图中没有奇数环。只要图中环的边数没奇数个数的,它就是二分图。
- 二分图可以是连通的,也可以是不连通的
- 树一定二分图。

染色法判定二分图
题目如下:
如果判断一个图是不是二分图?
- 开始对任意一未染色的顶点染色。
- 判断其相邻的顶点中,若未染色则将其染上和相邻顶点不同的颜色。
- 若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图,若颜色不同则继续判断。
- bfs和dfs可以搞定!
解题代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010 * 2;
int e[N], ne[N], idx;//邻接表存储图
int h[N];
int color[N];//保存各个点的颜色,0 未染色,1 是红色,2 是黑色
int n, m;//点和边void add(int a, int b)//邻接表插入点和边
{e[idx] = b, ne[idx]= h[a], h[a] = idx++;
}bool dfs(int u, int c)//深度优先遍历,参数1:点的编号 参数2:要染的颜色
{color[u] = c;//u的点成 c 染色//遍历和 u 相邻的点for(int i = h[u]; i!= -1; i = ne[i]){int b = e[i]; if(!color[b])//相邻的点没有颜色,则递归处理这个相邻点{if(!dfs(b, 3 - c)) return false;//(3 - 1 = 2, 如果 u 的颜色是2,则和 u 相邻的染成 1)//(3 - 2 = 1, 如果 u 的颜色是1,则和 u 相邻的染成 2)}else if(color[b] && color[b] != 3 - c)//如果已经染色,判断颜色是否为 3 - c{ return false;//如果不是,说明冲突,返回 }}return true;
}int main()
{memset(h, -1, sizeof h);//初始化邻接表cin >> n >> m;for(int i = 1; i <= m; i++)//读入边{int a, b;cin >> a >> b;add(a, b), add(b, a);}for(int i = 1; i <= n; i++)//遍历点{if(!color[i])//如果没染色{//以没染色的点为起点进行dfs搜索if(!dfs(i, 1))//染色该点,并递归处理和它相邻的点{cout << "No" << endl;//出现矛盾,输出NO return 0;}}}cout << "Yes" << endl;//全部染色完成,没有矛盾,输出YESreturn 0;
}算法板子:O(m+n),n表示点数,m表示边数
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色// 参数:u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{color[u] = c;for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (color[j] == -1){if (!dfs(j, !c)) return false;}else if (color[j] == c) return false;}return true;
}bool check()
{memset(color, -1, sizeof color);bool flag = true;for (int i = 1; i <= n; i ++ )if (color[i] == -1)if (!dfs(i, 0)){flag = false;break;}return flag;
}匈牙利算法
题目如下:

解题代码
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510, M = 100010;int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}int main()
{scanf("%d%d%d", &n1, &n2, &m);memset(h, -1, sizeof h);while (m -- ){int a, b;scanf("%d%d", &a, &b);add(a, b);}int res = 0;for (int i = 1; i <= n1; i ++ ){memset(st, false, sizeof st);if (find(i)) res ++ ;}printf("%d\n", res);return 0;
}算法板子:O(m*n),n表示点数,m表示边数
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{memset(st, false, sizeof st);if (find(i)) res ++ ;
}
相关文章:

二分图
目录 二分图 染色法判定二分图 匈牙利算法 二分图 二分图,又叫二部图,将所有点分成两个集合,使得所有边只出现在集合之间的点之间,而集合内部的点之间没有边。二分图当且仅当图中没有奇数环。只要图中环的边数没奇数个数的&am…...
[VUE]3-路由
目录 路由 Vue-Router1、Vue-Router 介绍2、路由配置3、嵌套路由3.1、简介3.2、实现步骤3.3、⭐注意事项 4、⭐router-view标签详解 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅…...

Kafka(六)消费者
目录 Kafka消费者1 配置消费者bootstrap.serversgroup.idkey.deserializervalue.deserializergroup.instance.idfetch.min.bytes1fetch.max.wait.msfetch.max.bytes57671680 (55 mebibytes)max.poll.record500max.partition.fetch.bytessession.timeout.ms45000 (45 seconds)he…...

RK3399平台入门到精通系列讲解(实验篇)共享工作队列的使用
🚀返回总目录 文章目录 一、工作队列相关接口函数1.1、初始化函数1.2、调度/取消调度工作队列函数二、信号驱动 IO 实验源码2.1、Makefile2.2、驱动部分代码工作队列是实现中断下半部分的机制之一,是一种用于管理任务的数据结构或机制。它通常用于多线程,多进程或分布式系统…...

STM32 基于 MPU6050 的飞行器姿态控制设计与实现
基于STM32的MPU6050姿态控制设计是无人机、飞行器等飞行器件开发中的核心技术之一。在本文中,我们将介绍如何利用STM32和MPU6050实现飞行器的姿态控制,并提供相应的代码示例。 1. 硬件连接及库配置 首先,我们需要将MPU6050连接到STM32微控制…...
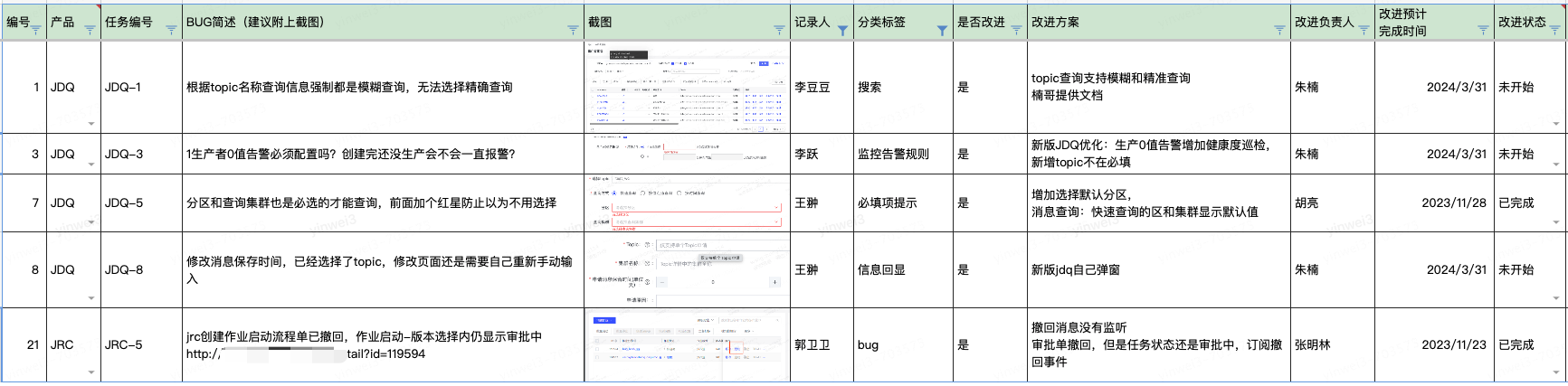
大数据平台Bug Bash大扫除最佳实践
一、背景 随着越来越多的"新人"在日常工作以及大促备战中担当大任,我们发现仅了解自身系统业务已不能满足日常系统开发运维需求。为此,大数据平台部门组织了一次Bug Bash活动,既能提升自己对兄弟产品的理解和使用,又能…...

JavaScript 中的数组过滤
在构建动态和交互式程序时,您可能需要添加一些交互式功能。例如,用户单击按钮以筛选一长串项目。 您可能还需要处理大量数据,以仅返回与指定条件匹配的项目。 在本文中,您将学习如何使用两种主要方法在 JavaScript 中过滤数组。…...
)
随机森林(Random Forest)
随机森林(Random Forest)是一种集成学习方法,通过组合多个决策树来提高模型的性能和鲁棒性。随机森林在每个决策树的训练过程中引入了随机性,包括对样本和特征的随机选择,以提高模型的泛化能力。以下是随机森林的基本原…...
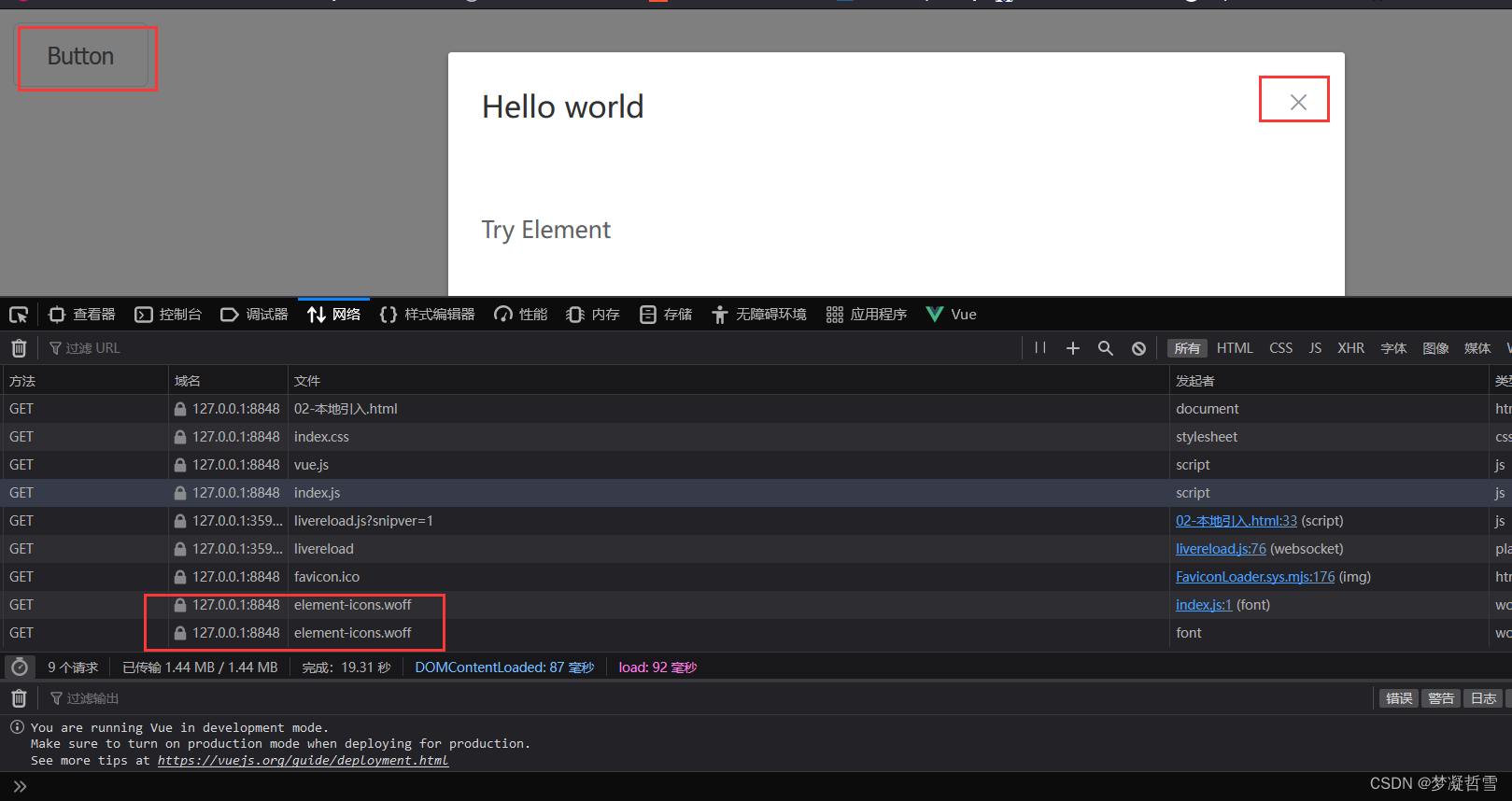
本地引入Element UI后导致图标显示异常
引入方式 npm 安装 推荐使用 npm 的方式安装,它能更好地和 webpack 打包工具配合使用。 npm i element-ui -SCDN 目前可以通过 unpkg.com/element-ui 获取到最新版本的资源,在页面上引入 js 和 css 文件即可开始使用。 <!-- 引入样式 --> <…...
UE5.1_UMG序列帧动画制作
UE5.1_UMG序列帧动画制作 UMG序列帧动画制作相对比较简单,不像视频帧需要创建媒体播放器那么复杂,以下简要说明: 1. 事件函数 2. 准备序列帧装入数组 3. 构造调用事件函数 4. 预览 序列帧UMG0105 5. 完成!按需配置即可。...

总结HarmonyOS的技术特点
HarmonyOS是华为自主研发的面向全场景的分布式操作系统。它的技术特点主要体现在以下几个方面: 分布式架构:HarmonyOS采用了分布式架构设计,通过组件化和小型化等方法,支持多种终端设备按需弹性部署,能够适配不同类别的…...

从0到1入门C++编程——04 类和对象之封装、构造函数、析构函数、this指针、友元
文章目录 一、封装二、项目文件拆分三、构造函数和析构函数1.构造函数的分类及调用2.拷贝函数调用时机3.构造函数调用规则4.深拷贝与浅拷贝5.初始化列表6.类对象作为类成员7.静态成员 四、C对象模型和this指针1.类的对象大小计算2.this指针3.空指针访问成员函数4.const修饰成员…...

Robot Operating System 2: Design, Architecture, and Uses In The Wild
Robot Operating System 2: Design, Architecture, and Uses In The Wild (机器人操作系统 2:设计、架构和实际应用) 摘要:随着机器人在广泛的商业用例中的部署,机器人革命的下一章正在顺利进行。即使在无数的应用程序和环境中,也…...

TinyEngine 服务端正式开源啦!!!
背景介绍 TinyEngine 低代码引擎介绍 随着企业对于低代码开发平台的需求日益增长,急需一个通用的解决方案来满足各种低代码平台的开发需求。正是在这种情况下,低代码引擎应运而生。它是一种通用的开发框架,通过对低代码平台系统常用的功能进…...

网页设计与制作web前端设计html+css+js成品。电脑网站制作代开发。vscodeDrea 【企业公司宣传网站(HTML静态网页项目实战)附源码】
网页设计与制作web前端设计htmlcssjs成品。电脑网站制作代开发。vscodeDrea 【企业公司宣传网站(HTML静态网页项目实战)附源码】 https://www.bilibili.com/video/BV1Hp4y1o7RY/?share_sourcecopy_web&vd_sourced43766e8ddfffd1f1a1165a3e72d7605...

Avalonia学习(二十)-登录界面演示
今天开始继续Avalonia练习。 本节:演示实现登录界面 在网上看见一个博客,展示Avalonia实现,仿照GGTalk,我实现了一下,感觉是可以的。将测试的数据代码效果写下来。主要是样式使用,图片加载方式。 只有前…...

Spring依赖注入的魔法:深入DI的实现原理【beans 五】
欢迎来到我的博客,代码的世界里,每一行都是一个故事 Spring依赖注入的魔法:深入DI的实现原理【beans 五】 前言DI的基本概念基本概念:为什么使用依赖注入: 构造器注入构造器注入的基本概念:示例:…...
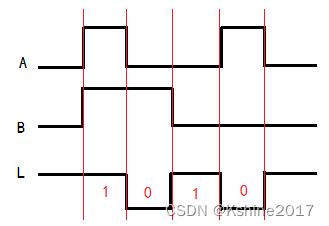
【学习笔记】1、数字逻辑概论
1.1 数字信号 数字信号,在时间和数值上均是离散的。数字信号的表达方式:二值数字逻辑和逻辑电平描述的数字波形。 (1) 数字波形的两种类型 数值信号又称为“二值信号”。数字波形又称为“二值位形图”。 什么是一拍 一定的时…...

设置代理IP地址对网络有什么影响?爬虫代理IP主要有哪些作用?
在互联网的广泛应用下,代理IP地址成为了一种常见的网络技术。代理IP地址可以改变用户的上网行为,进而影响网络访问的速度和安全性。本篇文章将探讨设置代理IP地址对网络的影响,以及爬虫代理IP的主要作用。 首先,让我们来了解一下代…...

聊聊jvm的mapped buffer的统计
序 本文主要研究一下jvm的mapped buffer的统计 示例 private void writeDirectBuffer() {// 分配一个256MB的直接缓冲区ByteBuffer buffer ByteBuffer.allocateDirect(256 * 1024 * 1024);// 填充数据Random random new Random();while (buffer.remaining() > 4) {buff…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
