【学习笔记】1、数字逻辑概论
1.1 数字信号
- 数字信号,在时间和数值上均是离散的。
- 数字信号的表达方式:二值数字逻辑和逻辑电平描述的数字波形。
(1) 数字波形的两种类型
- 数值信号又称为“二值信号”。数字波形又称为“二值位形图”。
什么是一拍
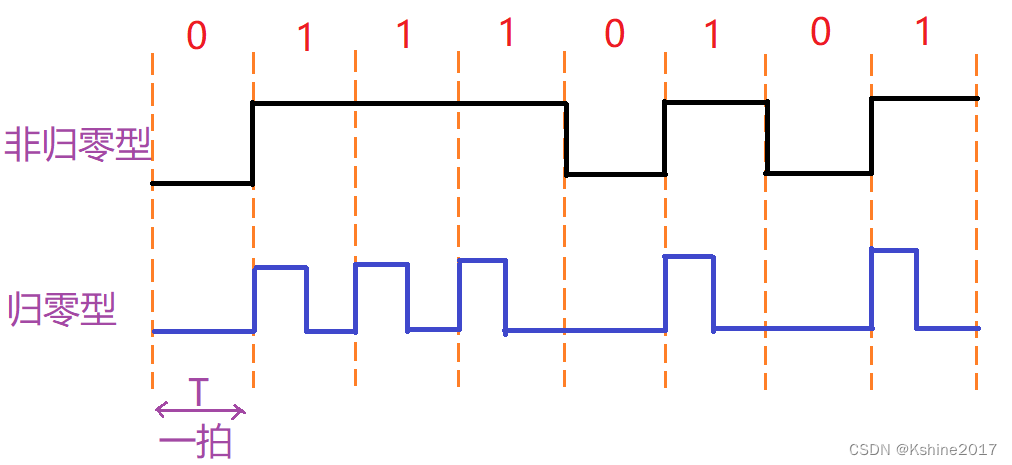
- 一定的时间间隔T,称为1bit,或者1拍。
非归零型,数字波形
- 在一个时间拍内,高电平1,低电平0。
- 大多数数值信号都是非归零型。
- 非归零信号,每位数据占用一个位时间T。每秒钟传输数据的位数称为数据率(比特率)。
归零型,数值波形
- 在一个时间拍内,有脉冲表示1,无脉冲表示0。
- 只有作为时序控制信号使用的时钟脉冲是归零型。
(2)周期性和非周期性
- 周期性数字波形,常用周期T和频率f来描述。
占空比=脉宽/周期
q ( % ) = t w T ∗ 100 % q(\%)= \frac{t_w}{T} *100\% q(%)=Ttw∗100% - 占空比为50%的矩形脉冲,被称为“方波”。此时0和1交替出现,时间相同。
(3)实际数字信号波形
- 上升时间tr,脉冲幅度从10%-90%所经历的时间。几纳秒。
- 下降时间tf,脉冲幅度从90%-10%所经历的时间。几纳秒。
- 脉冲宽度tw,脉冲幅度50%的两个时间点的时间间隔。
(4)时序图
- 数字电路中,常用时序图或者脉冲波形图,来分析逻辑。
1.2 数制
(1)十进制
- 任何一个数,都可以用0123456789等是个数码中的一个或几个,按照一定的规律排列起来表示。
- 逢十进一。9+1=10(十)。
- 十进制是以10为基数的计数体制。
- 用数字电路来存储或者处理十进制数是很不方便的。因为构成数字电路的基本思路是把电路的状态与数码对应起来。
(2)二进制
- 只有0和1两个数码。
- 逢二进一。1+1=10(壹零)。
- 二进制是以2为基础的计数体制。
- 二进制的数字装置简单可靠,可用元件少。易于电路实现。
- 二进制的基本运算规则简单,运算操作方便。位数太多。
(3)十 - 二进制之间的转换
-
二进制转为十进制
( 1010110 ) B = 1 ∗ 2 6 + 0 ∗ 2 5 + 1 ∗ 2 4 + 0 ∗ 2 3 + 1 ∗ 2 2 + 1 ∗ 2 1 + 0 ∗ 2 0 = ( 86 ) D (1010110)_B = 1 * 2^6 + 0 * 2^5 + 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 = (86)_D (1010110)B=1∗26+0∗25+1∗24+0∗23+1∗22+1∗21+0∗20=(86)D -
十进制转为二进制
( 37 ) D = ( 100101 ) B (37)_D = (100101)_B (37)D=(100101)B

( 0.706 ) D = ( 0.101101001 ) B (0.706)_D = (0.101101001)_B (0.706)D=(0.101101001)B
要求误差不大于2^-10。
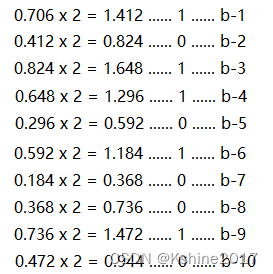
(4)十六进制和八进制
- 为了方便书写和记忆,在计算机资料中,常用十六进制或者八进制表示数值。与二进制之间转换容易。
- 十六进制有十六个数码,0123456789abcdef。
- 十六进制,逢十六进一。
- 十六进制是以16为基数的计数体制。
- 八进制有八个数码,01234567。
- 八进制,逢八进一。
1.3 二进制数的算术运算
(1)无符号二进制数的算术运算
- 二进制加法。
- 二进制减法。无符号减法计算,要求被减数一定要大于减数。
- 乘法运算和除法运算。可以使用类似于10进制乘除的方法。
(2)带符号二进制数的减法运算
-
十进制的补码表示。
-
R表示基数,在二进制时,R=2,十进制时,R=10。
-
N表示原码。
-
n表示位数。
( N ) 补 = R n − N (N)_补 = R^n - N (N)补=Rn−N
− N = ( N ) 补 − R n -N = (N)_补 -R^n −N=(N)补−Rn -
以十进制为例,2的补码 = 10^1 - 2 = 8
-
以十进制为例,46的补码 = 10^2 - 46 = 54
8 − 2 = 8 + ( 2 ) 补 − 10 = 8 + 8 − 10 = 6 8 - 2 = 8 + (2)_补 - 10 = 8 +8 - 10 = 6 8−2=8+(2)补−10=8+8−10=6 -
二进制的补码表示。
-
补码或者反码的最高位为符号位,正0,负1。
-
当二进制数为正数时,其补码,反码,原码相同。
-
当二进制数为负数时,对原码的数值位进行“取反加一”,得到补码。
1.4 二进制代码
- 数字系统中,信息可分为“数值”或者“文字符号”。
- 文字符号也可以使用二进制数码表示。这些数码不表示数量的大小,仅用于区别不同的事物。
- 称呼这样的二进制数码为“代码”。
- 编码: 以一定的规则编制“代码”的过程(十进制数值、字母、符号等实际含义 -> “代码”)。
- 译码:将“代码” 还原成实际含义的过程。
(1)二-十进制码
- 二-十进制码,Binnary Coded Decimal 。BCD码。
- 用4位二进制数,表示1位十进制数。
- 8421BCD码。“有权码”。自然二进制数的前10种组合。
- 2421BCD码。“有权码”。“自补码”。各数的“代码”,取反之后的“代码”,与原数“代码”关于9互补。
- 5421BCD码。“有权码”。
- 余3码。 “无权码”。8421+3得到“余三码”。具有“自补性”。
- 余3循环码。 “无权码”。“相邻性”。“格雷码”去掉首尾各自3种状态得到“余3循环码”
(2)格雷码
- 无权码,相邻只变一位。
- 模拟量 转换 成 数值时,用文字符号表示其数值。当模拟量发生微小变化而引发数值量从1位变化到相邻位时,格雷码可以保证只有一位变化。
- 细微的模拟量变化,如果发生多位位值变化的情况,在硬件实现时,不能保证多位同时翻转到最终值,会出现瞬间的错误码。
- 细微模拟量变化时,格雷码可以避免错误码的出现。
(3)ASCII码
- 使用7位二进制码,表示128个文字字符,包括十进制数码元,英文大小写,控制符,运算符,特殊符号。
1.5 二值逻辑变量与基本逻辑运算
- 逻辑运算 不是 算术运算。
- 逻辑变量可以用ABCxyz等字母表示。
- 逻辑变量的取值只能是0和1。表示完全对立的逻辑状态。
(1)与运算
- 运算符号:“·”点乘(可以省略)。或者“∧” 和“∩”。
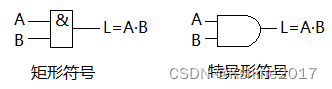
- 与逻辑真值表
| A | B | L=A·B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
(2)或运算
- 运算符号:“+” 。或者“∨”和“∪”。
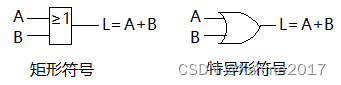
| A | B | L=A+B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
(3)非运算
- 运算符号:“ ̄”。或者“~”,“ ’ ’” ,“ ﹁”。
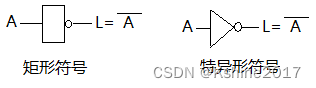
| A | L= A ‾ \overline{\text{A}} A |
|---|---|
| 0 | 1 |
| 1 | 0 |
(3)几种常用逻辑运算
- 与非
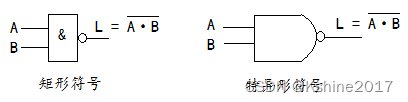
| A | B | L= A ⋅ B ‾ \overline{A·B} A⋅B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 或非
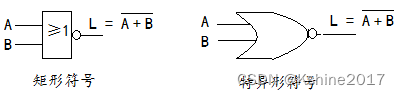
| A | B | L= A + B ‾ \overline{A+B} A+B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
- 异或
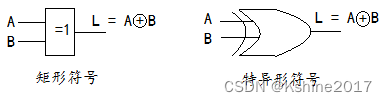
| A | B | L= A ‾ \overline{A} AB+A B ‾ \overline{B} B=A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 同或
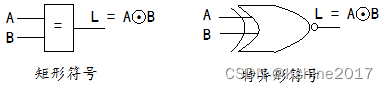
| A | B | L= AB+ A B ‾ \overline{AB} AB=A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
1.6 逻辑函数及其表示方法
- 输入逻辑变量,只取0或1
- 输出逻辑变量,只取0或1
- 逻辑函数。
- 逻辑函数的描述方法有:真值表、逻辑函数表达式、逻辑图、波形图、卡诺图。
(1)真值表
| A | B | L= AB+ A B ‾ \overline{AB} AB=A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
(2)逻辑表达式
L= AB+ A B ‾ \overline{AB} AB=A⊙B
(3)逻辑图表示方法
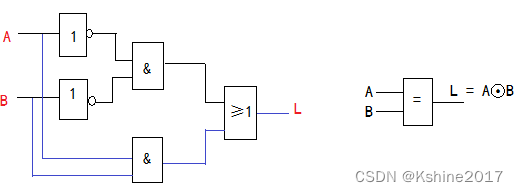
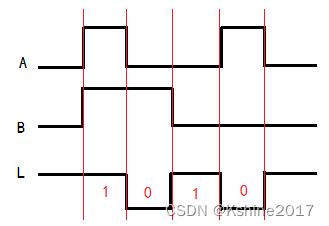
(4)波形图表示方法
相关文章:

【学习笔记】1、数字逻辑概论
1.1 数字信号 数字信号,在时间和数值上均是离散的。数字信号的表达方式:二值数字逻辑和逻辑电平描述的数字波形。 (1) 数字波形的两种类型 数值信号又称为“二值信号”。数字波形又称为“二值位形图”。 什么是一拍 一定的时…...

设置代理IP地址对网络有什么影响?爬虫代理IP主要有哪些作用?
在互联网的广泛应用下,代理IP地址成为了一种常见的网络技术。代理IP地址可以改变用户的上网行为,进而影响网络访问的速度和安全性。本篇文章将探讨设置代理IP地址对网络的影响,以及爬虫代理IP的主要作用。 首先,让我们来了解一下代…...

聊聊jvm的mapped buffer的统计
序 本文主要研究一下jvm的mapped buffer的统计 示例 private void writeDirectBuffer() {// 分配一个256MB的直接缓冲区ByteBuffer buffer ByteBuffer.allocateDirect(256 * 1024 * 1024);// 填充数据Random random new Random();while (buffer.remaining() > 4) {buff…...

matrix-breakout-2-morpheus 靶场 练习思路
arp-scan -l 获取目标机器的IP nmap -sV -A IP 查看目标机器开放的端口 gobuster dir -u http://192.168.29.130 -x php,txt,jsp,asp -w /usr/share/wordlists/dirbuster/directory-list-2.3-medium.txt 爆破目标机器的文件目录,找到可以访问的文件路径 http://192.168…...

【Flutter 开发实战】Dart 基础篇:从了解背景开始
想要学会用 Flutter 开发 App,就不可避免的要学习另一门很有意思的编程语言 —— Dart。很多小伙伴可能在学习 Flutter 之前可能都没听说过这门编程语言,我也是一样,还以为 Dart 是为了 Flutter 而诞生的;然而,当我们去…...

西电期末1017.有序序列插值
一.题目 二.分析与思路 简单题。主要考察简单的排序,最后的插入数据同样不用具体实现,只需在输出时多输出一下即可,注意顺序!! 三.代码实现 #include<bits/stdc.h>//万能头 int main() {int n;scanf("%d…...
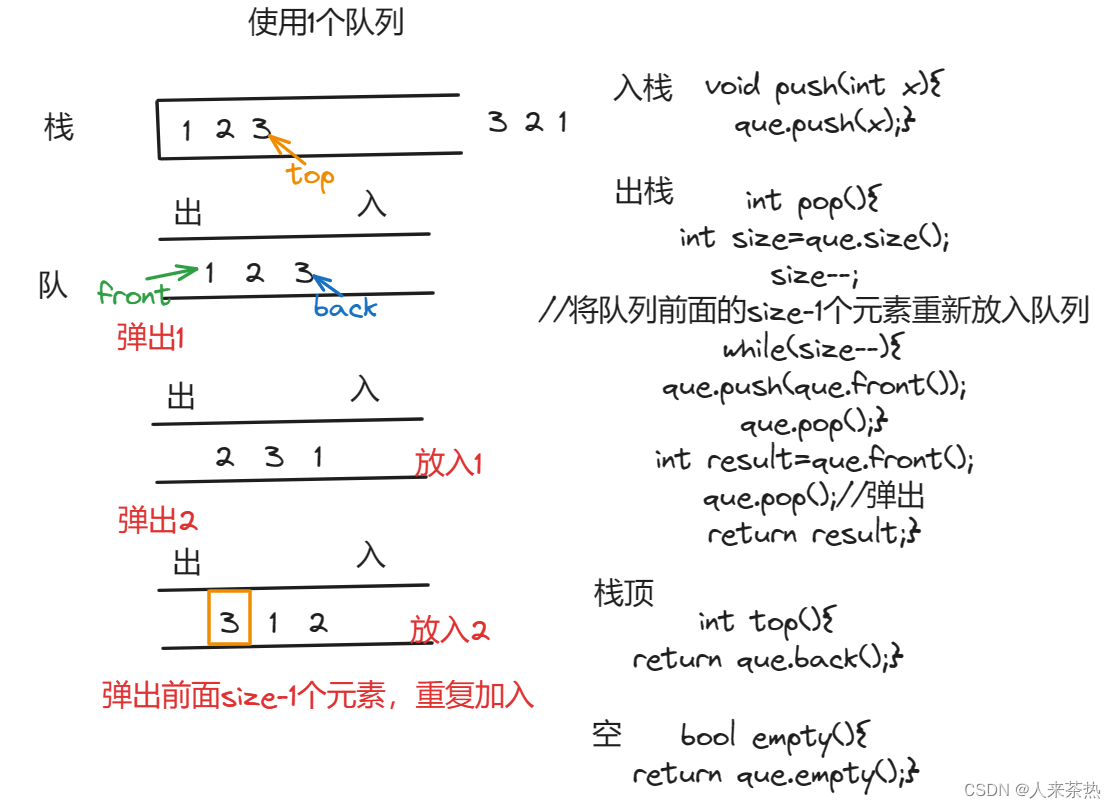
day10 用栈实现队列 用队列实现栈
题目1:232 用栈实现队列 题目链接:232 用栈实现队列 题意 用两个栈实现先入先出队列(一个入栈,一个出栈),实现如下功能: 1)push:将元素x推到队列末尾 2)…...
)
解决跨域问题(SpringBoot)
“什么是跨域?” 跨域 (Cross-Origin) 是指在浏览器的同源策略(Same-Origin Policy)下,一个网页的源(指协议、域名、端口号的组合)与另一个网页的源不同。因此,不同源的…...

LeetCode——2487. 从链表中移除节点
通过万岁!!! 题目:给你一个链表,然后让你从链表中移除一些节点,移除的规则就是我们选择的这个节点在原链表中往右不能有比这个节点大的值。思路:这个题我最开始以为是双指针,然后找…...

云原生和Kubernetes如何简化应用程序开发
在谈论当前技术时,“云计算”正变得非常普遍,作为开发人员,将会继续体验使用云计算应用程序的优势;在云计算中,另一个正在出现的术语是云原生。在进入实际话题之前,首先了解一下云原生到底是什么。 深入了解云原生应用 现在,世界各地的公司都了解云计算应用程序可以带来…...
)
点云从入门到精通技术详解100篇-基于深度学习的室内场景三维点云语义分割(续)
目录 CSegNet 语义分割模型构建 3.1 引言 3.2 偏移注意机制 3.3 网络主干 3.4 边缘卷积模块...

RabbitMQ消息可靠性保证机制3--消费端ACK机制
消费端ACK机制 在这之前已经完成了发送端的确认机制。可以保证数据成功的发送到RabbitMQ,以及持久化机制,然尔这依然无法完全保证整个过程的可靠性,因为如果消息被消费过程中业务处理失败了,但是消息却已经被标记为消费了&…...

Copilot在Pycharm的应用和示例
Copilot 是 Github 在 2021 年发布的 AI 代码助手工具,它可以根据你提供的上下文信息,自动生成代码建议,帮助提高代码编写效率和准确性。在 Pycharm 中使用 Copilot,可以进一步提升 Python 开发效率,本文将分享如何在 …...

搜维尔科技:【简报】第九届元宇宙数字人设计大赛,报名已经进入白热化阶段!
随着元宇宙时代的来临,数字人设计成为了创新前沿领域之一。为了提高大学生元宇宙虚拟人角色策划与美术设计的专业核心能力,我们特别举办了这场元宇宙数字人设计赛道,赛道主题为「AI人工智能科技」 ,只要与「AI人工智能科技」相关的…...
)
性能检测自动化(含内存泄露检测)
一、平台侧实现方案 1、UI case重复执行N次:进入页面,sleep 5s,记录start_time,sleep 30s,记录end_time,性能采集工具全程采集性能数据 2、根据采集到的性能数据,按照N次卡点性能数据:去掉最大的10%、最小的10%,求取平均值,作为单次性能数据结果f(n)…...

iec104和iec61850
iec104和iec61850 IEC104 规约详细解读(一) 协议结构 IEC104 规约详细解读(二)交互流程以及协议解析 61850开发知识总结与分享【1】 Get the necesarry projects next to each other in the same directory; $ git clone https://github.com/robidev/iec61850_open_server.g…...

redis 面试问题 (更新中 ing)
目录 reids 是做什么的为什么那么快有哪些使用场景redis有哪些 数据结构redis 有哪些底层数据结构为什么设计 sds一个 字符串 存储多大容量 stream为什么设计 streamstream 消费者消息丢失stream 消息私信问题 持久化机制redis 持久化机制,优缺点,怎么用…...
第389题找不同(Python))
力扣(leetcode)第389题找不同(Python)
389.找不同 题目链接:389.找不同 给定两个字符串 s 和 t ,它们只包含小写字母。 字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母。 请找出在 t 中被添加的字母。 示例 1: 输入:s “abcd”, t “abcde…...

Linux_源码编译安装LAMP
1. 安装httpd服务 在配置 Apache 网站服务之前,需要正确安装好 httpd 服务器软件。httpd 服务器的安装可以选用 RPM 安装、源码编译安装这两种方式,前者相对比较简单、快速,但是在功能上存在一定的局限性。在实际的生产环境中,使…...
静态网页设计——清雅古筝网(HTML+CSS+JavaScript)
前言 声明:该文章只是做技术分享,若侵权请联系我删除。!! 感谢大佬的视频: https://www.bilibili.com/video/BV1T64y1K7Zn/?vd_source5f425e0074a7f92921f53ab87712357b 使用技术:HTMLCSSJS(…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
