视频云存储/视频智能分析平台EasyCVR在麒麟系统中无法启动该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安防视频监控的能力,也具备接入AI智能分析的能力,可拓展性强、视频能力灵活,能对外分发RTMP、RTSP、HTTP-FLV、WebSocket-FLV、HLS、WebRTC等视频流。

有用户反馈,EasyCVR在麒麟系统中无法启动程序,于是请求技术人员帮助。收到问题后,技术人员立即进行排查分析和解决。
1)首先排查日志发现,日志中无任何错误日志,但在启动./start.sh 系统时就会出现崩溃;
2)继续使用./easycvr,显示可以正常启动,并无任何报错,程序也在正常运行;
3)排查发现,老版本显示正常,但使用新版本(V.3.4)时,./statr.sh 系统就会崩溃;
4)经过对比发现新版本下的./start.sh 没有可执行权限从而导致麒麟系统崩溃;

5)只需在新版本EasyCVR目录下执行 chmod +x ./start.sh 即可。
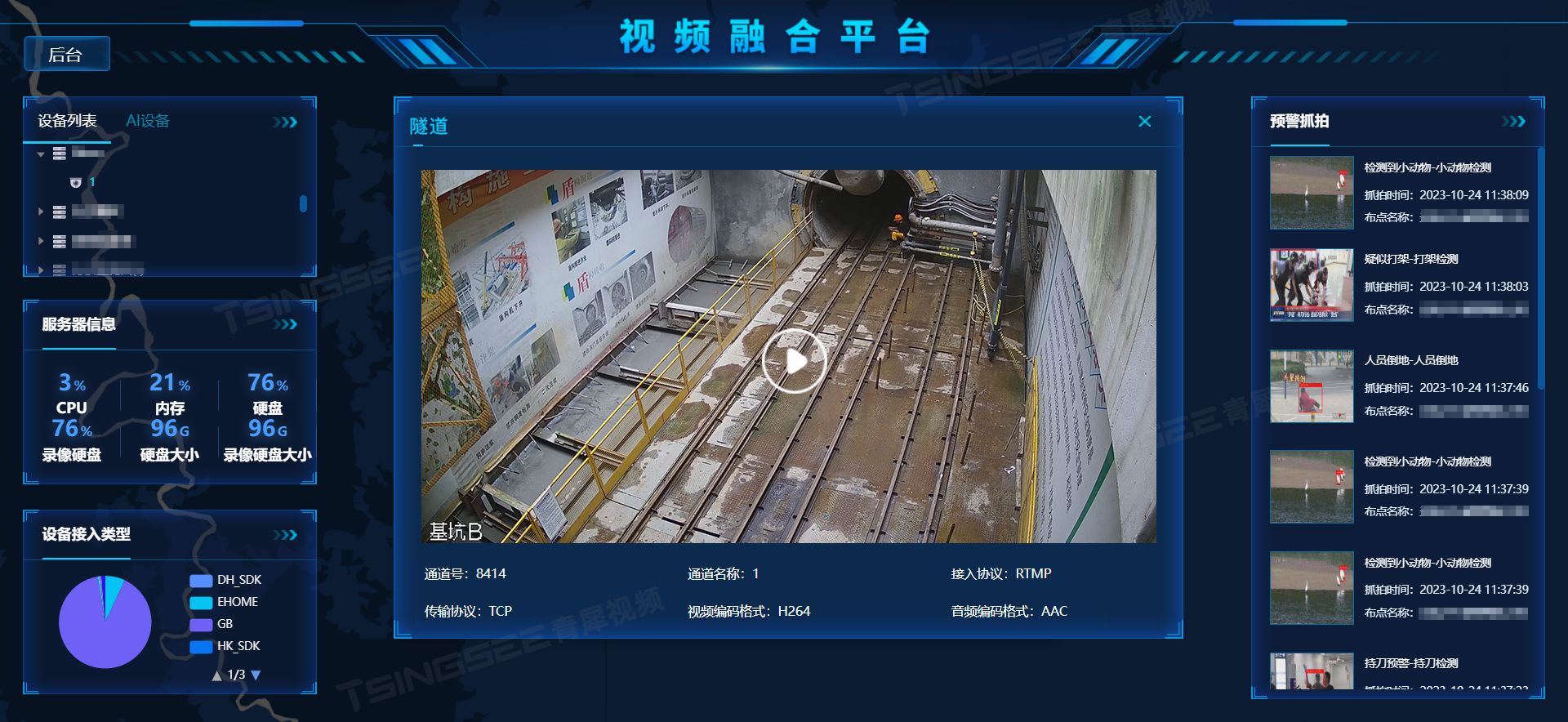
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。GB28181视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、H.265自动转码H.264、平台级联等。感兴趣的用户可以前往演示平台进行体验或部署测试。
相关文章:

视频云存储/视频智能分析平台EasyCVR在麒麟系统中无法启动该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
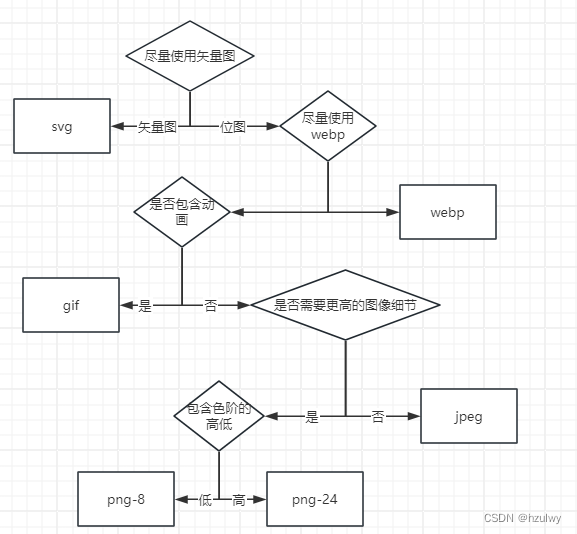
前端性能优化之图像优化
图像优化问题主要可以分为两方面:图像的选取和使用,图像的加载和显示。 图像基础 HTTP Archive上的数据显示,网站传输的数据中,60%的资源都是由各种图像文件组成的,当然这些是将各类型网站平均的结果,单独…...
微信小程序封装vant 下拉框select 单选组件
先上效果图: 主要是用vant 小程序组件封装的:vant 小程序ui网址:vant-weapp 主要代码如下: 先封装子组件: select-popup 放在 components 文件夹里面 select-popup.wxml: <!--pages/select-popup/select-popup.wxml--> &…...

c语言试卷
江西财经大学IT帮 2020-2021第一学期期末C语言模拟考试试卷 课程名称:C语言程序设计(软件)(主干课程) 适用对象:21级本科 试卷命题人 钟芳盛 游天悦 李俊贤 万军豪 张位 试卷审核人 钟芳盛 一、单项…...

文献阅读:Sparse Low-rank Adaptation of Pre-trained Language Models
文献阅读:Sparse Low-rank Adaptation of Pre-trained Language Models 1. 文章简介2. 具体方法介绍 1. SoRA具体结构2. 阈值选取考察 3. 实验 & 结论 1. 基础实验 1. 实验设置2. 结果分析 2. 细节讨论 1. 稀疏度分析2. rank分析3. 参数位置分析4. 效率考察 4.…...
NCC基础开发技能培训
YonBuilder for NCC 是一个带插件的eclipse工具,跟eclipse没什么区别 NC Cloud2021.11版本开发环境搭建改动 https://nccdev.yonyou.com/article/detail/495 不管是NC Cloud 新手还是老NC开发,在开发NC Cloud时开发环境搭建必看!ÿ…...
Flink中的状态管理
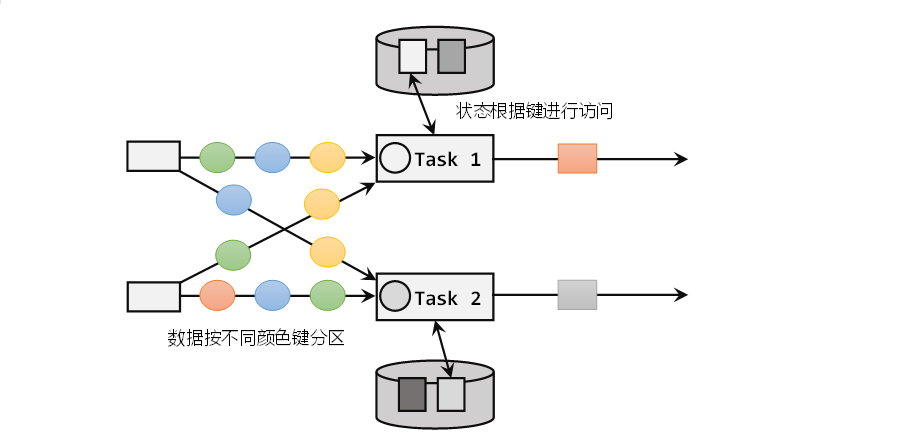
一.Flink中的状态 1.1 概述 在Flink中,算子任务可以分为有状态和无状态两种状态。 无状态的算子任务只需要观察每个独立事件,根据当前输入的数据直接转换输出结果。例如Map、Filter、FlatMap都是属于无状态算子。 而有状态的算子任务,就…...

【linux】线程互斥
线程互斥 1.线程互斥2.可重入VS线程安全3.常见锁的概念 喜欢的点赞,收藏,关注一下把! 1.线程互斥 到目前为止我们学了线程概念,线程控制接下来我们进行下一个话题,线程互斥。 有没有考虑过这样的一个问题,…...

机器学习原理到Python代码实现之LinearRegression
Linear Regression 线性回归模型 该文章作为机器学习的第一篇文章,主要介绍线性回归模型的原理和实现方法。 更多相关工作请参考:Github 算法介绍 线性回归模型是一种常见的机器学习模型,用于预测一个连续的目标变量(也称为响应变…...

Hive SQL / SQL
1. 建表 & 拉取表2. 插入数据 insert select3. 查询3.1 查询语句语法/顺序3.2 关系操作符3.3 聚合函数3.4 where3.5 分组聚合3.6 having 筛选分组后结果3.7 显式类型转换 & select产生指定值的列 4. join 横向拼接4.1 等值连接 & 不等值连接4.2 两表连接4.2.1 内连…...

程序媛的mac修炼手册--MacOS系统更新升级史
啊,我这个口罩三年从未感染过新冠的天选免疫王,却被支原体击倒😷大意了,前几天去医院体检,刚检查完出医院就摘口罩了🤦大伙儿还是要注意戴口罩,保重身体啊!身体欠恙,就闲…...

【数据库原理】(9)SQL简介
一.SQL 的发展历史 起源:SQL 起源于 1970 年代,由 IBM 的研究员 Edgar F. Codd 提出的关系模型概念演化而来。初期:Boyce 和 Chamberlin 在 IBM 开发了 SQUARE 语言的原型,后发展成为 SQL。这是为了更好地利用和管理关系数据库。…...

第二百五十二回
文章目录 概念介绍实现方法示例代码 我们在上一章回中介绍了如何在页面中添加图片相关的内容,本章回中将介绍如何给组件添加阴影.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在本章回中介绍的阴影类似影子,只是它不像影子那么明显&a…...
)
Leetcode 3701 · Find Nearest Right Node in Binary Tree (遍历和BFS好题)
3701 Find Nearest Right Node in Binary TreePRE Algorithms This topic is a pre-release topic. If you encounter any problems, please contact us via “Problem Correction”, and we will upgrade your account to VIP as a thank you. Description Given a binary t…...

网站被攻击了,接入CDN对比直接使用高防服务器有哪些优势
网站是互联网行业中经常被攻击的目标之一。攻击是许多站长最害怕遇到的情况。当用户访问一个网站,页面半天打不开,响应缓慢,或者直接打不开,多半是会直接走开,而不是等待继续等待相应。针对网站攻击的防护,…...

location常用属性和方法
目录 Location 对象 Location 对象属性 Location 对象方法 location.assign() location.replace() location.reload() Location 对象 Location 对象包含有关当前 URL 的信息。Location 对象是 Window 对象的一个部分,可通过 window.location 属性来访问。 L…...

二分图
目录 二分图 染色法判定二分图 匈牙利算法 二分图 二分图,又叫二部图,将所有点分成两个集合,使得所有边只出现在集合之间的点之间,而集合内部的点之间没有边。二分图当且仅当图中没有奇数环。只要图中环的边数没奇数个数的&am…...
[VUE]3-路由
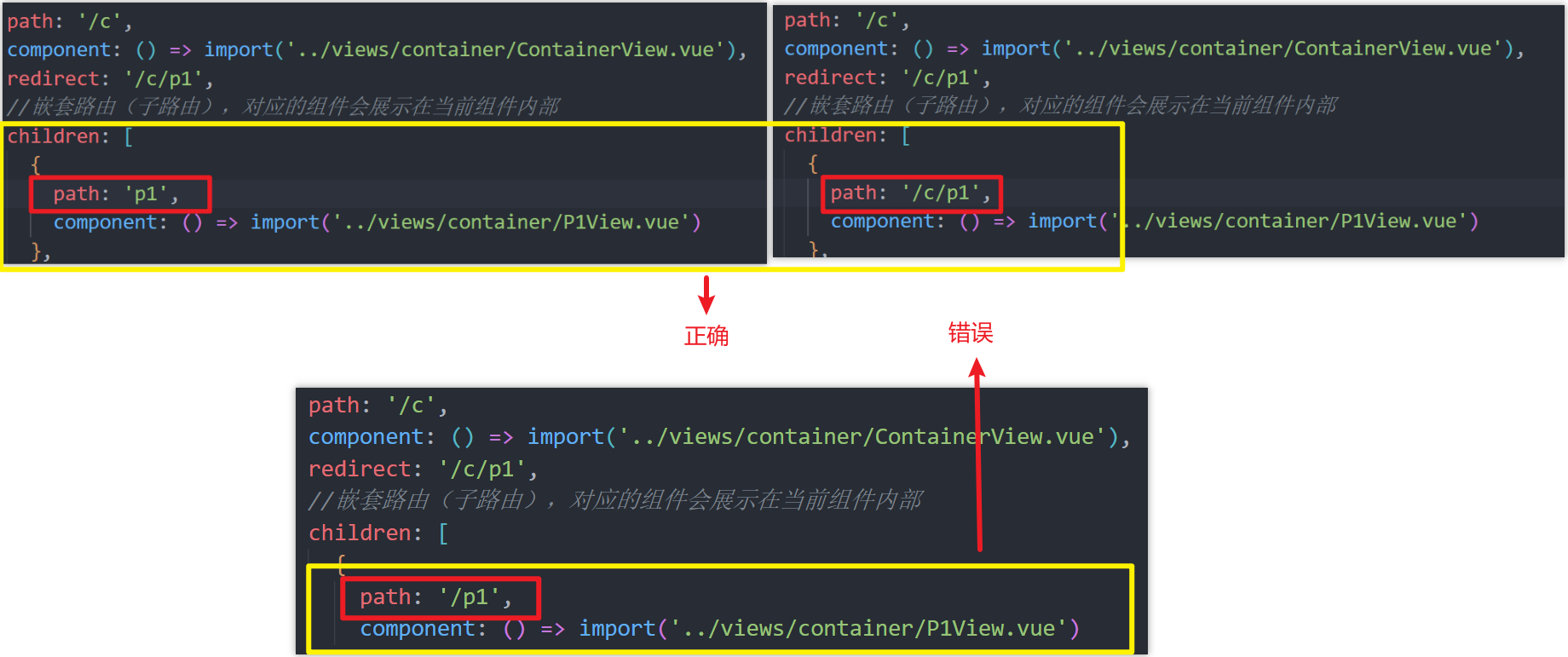
目录 路由 Vue-Router1、Vue-Router 介绍2、路由配置3、嵌套路由3.1、简介3.2、实现步骤3.3、⭐注意事项 4、⭐router-view标签详解 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅…...

Kafka(六)消费者
目录 Kafka消费者1 配置消费者bootstrap.serversgroup.idkey.deserializervalue.deserializergroup.instance.idfetch.min.bytes1fetch.max.wait.msfetch.max.bytes57671680 (55 mebibytes)max.poll.record500max.partition.fetch.bytessession.timeout.ms45000 (45 seconds)he…...

RK3399平台入门到精通系列讲解(实验篇)共享工作队列的使用
🚀返回总目录 文章目录 一、工作队列相关接口函数1.1、初始化函数1.2、调度/取消调度工作队列函数二、信号驱动 IO 实验源码2.1、Makefile2.2、驱动部分代码工作队列是实现中断下半部分的机制之一,是一种用于管理任务的数据结构或机制。它通常用于多线程,多进程或分布式系统…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
