【面试高频算法解析】算法练习2 回溯(Backtracking)
前言
本专栏旨在通过分类学习算法,使您能够牢固掌握不同算法的理论要点。通过策略性地练习精选的经典题目,帮助您深度理解每种算法,避免出现刷了很多算法题,还是一知半解的状态
专栏导航
- 二分查找
- 回溯(Backtracking)
- 双指针
- 滑动窗口
- 深度优先搜索
- 广度优先搜索
- 贪心算法
- 单调队列
- 堆(Heap)
算法解析
回溯(Backtracking)是一种通过试错来解决问题的算法思想。当它通过尝试分步去解决一个问题时,如果发现现有的分步答案不能得到有效的正确的解答时,它将取消上一步甚至是上几步的计算,再通过其他的可能的分步解答再次尝试寻找问题的答案。
回溯法通常用递归方式来实现,在解决问题的过程中尝试各种可能的分步方法。如果某一步骤失败了,回溯算法会退回到上一步骤,然后尝试另一种方法。回溯法常用于解决如下问题:
- 组合问题:求解一个问题的所有满足条件的组合方式。
- 排列问题:求解一个问题的所有满足条件的排列方式。
- 划分问题:求解将一个对象分成几部分的方法。
- 子集构造问题:求解一个集合的所有子集。
- 棋盘问题:如八皇后问题、解数独和跳马问题等。
- 图的遍历问题:如哈密顿路径问题、图的着色问题等。
回溯算法的关键在于解决决策树的遍历过程中,如何剪枝。剪枝通过检测是否已经不可能得到正确的解来减少不必要的计算。在实现回溯算法时,通常有以下几个步骤:
- 选择:选择下一个可能的分步解答。
- 约束:检查到目前为止的解答序列是否满足约束条件(即是否“合法”)。
- 目标:检查到目前为止的解答序列是否满足解答条件(即是否已经找到一个解答)。
如果以上步骤中的任何一步不能继续下去,那么就执行回溯(返回上一步),尝试其他可能的路径。这种算法可以看作穷举搜索的一种优化,它利用问题的约束条件大大减少了搜索空间。
回溯算法和深度优先搜索(DFS)有密切的关系,实际上,回溯算法可以视为带有剪枝功能的深度优先搜索。在实现时,通常使用递归方法来模拟整个决策树的深度优先遍历过程,递归结构的本质上是栈结构,与DFS的实现方式一致。
实战练习
组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
官方题解
全排列II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10
官方题解
单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
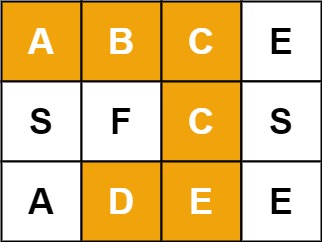
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出:true
示例 2:
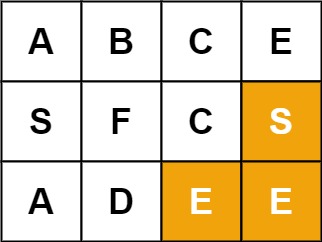
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
输出:true
示例 3:

输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
输出:false
提示:
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成
进阶: 你可以使用搜索剪枝的技术来优化解决方案,使其在 board 更大的情况下可以更快解决问题?
官方题解
相关文章:

【面试高频算法解析】算法练习2 回溯(Backtracking)
前言 本专栏旨在通过分类学习算法,使您能够牢固掌握不同算法的理论要点。通过策略性地练习精选的经典题目,帮助您深度理解每种算法,避免出现刷了很多算法题,还是一知半解的状态 专栏导航 二分查找回溯(Backtracking&…...

认识Git
🌎初识Git 初识Git 什么是Git Git的安装 Centos平台安装Git Ubuntu平台安装Git Git的基本操作 创建远程仓库 配置Git 认识工作区、暂存区与版本库 添加文件到暂存区 将暂存区文件提交至本…...

@RequestParam,@RequestBody和@PathVariable 区别
RequestParam,RequestBody和PathVariable 这三者是spring常见的接受前端数据的注解,那么他们分别是接受什么的前端数据呢? RequestParam:这个注解主要用于处理请求参数,尤其是GET请求中的查询参数和表单参数。它可以用…...

vue3组件传参
1、props: 2、自定义事件子传父 3、mitt任意组件通讯 4、v-model通讯(v-model绑定在组件上) (1)V2中父子组件的v-model通信,限制了popos接收的属性名必须为value和emit触发的事件名必须为input,所以有时会有冲突; 父组件: 子组件: (2)V3中:限制了popos接收的属性名…...

React16源码: React中创建更新的方式及ReactDOM.render的源码实现
React当中创建更新的主要方式 ReactDOM.render || hydrate 这两个API都是我们要把整个应用第一次进行渲染到我们的页面上面能够展现出来我们整个应用的样子的一个过程这是初次渲染 setState 后续更新应用 forceUpdate 后续更新应用 replaceState 在后续被舍弃 关于 ReactDOM…...

CentOS 7 系列默认的网卡接口名称
CentOS 7 系列默认的网卡接口是随机的,如果要修改网卡名称以 eth 开头,有两种方式。 方法一:安装系统时 在安装界面移动光标到 Install Centos 7.按 TAB 键 在出现的代码的末尾添加:net.ifnames0 biosdevname0.按下回车开始安装即…...

多文件上传
HTML中实现多文件上传是通过用<input type"file">元素的multiple属性,以下简单描述多文件上传的步骤 HTML表单准备,使用<input type"file">元素,并为其添加multiple属性,以允许用户选择多个文件…...

2024.1.7力扣每日一题——赎金信
2024.1.7 题目来源我的题解方法一 哈希表方法二 数组 题目来源 力扣每日一题;题序:383 我的题解 方法一 哈希表 使用哈希表记录ransomNote中所需字符的数量,然后遍历magazine并将哈希表中存在的对应的数量减一 时间复杂度:O(nm…...

C#中List<T>底层原理剖析
C#中List底层原理剖析 1. 基础用法2. List的Capacity与Count:3.List的底层原理3.1. 构造3.2 Add()接口3.3 Remove()接口3.4 Inster()接口3.5 Clear()接口3.6 Contains()接口3.7 ToArray()接口3.8 Find()接口3.8 Sort()接口 4. 总结5. 参考 1. 基础用法 list.Max() …...

Leetcode 3003. Maximize the Number of Partitions After Operations
Leetcode 3003. Maximize the Number of Partitions After Operations 1. 解题思路2. 代码实现 题目链接:10038. Maximize the Number of Partitions After Operations 1. 解题思路 这一题我看实际比赛当中只有72个人做出来,把我吓得够呛,…...
)
MySQL第一讲:MySQL知识体系详解(P6精通)
MySQL知识体系详解(P6精通) MySQL不论在实践还是面试中,都是频率最高的。本系列主要对MySQL知识体系梳理,将给大家构建JVM核心知识点全局知识体系,本文是MySQL第一讲,MySQL知识体系详解。 文章目录 MySQL知识体系详解(P6精通)1、MySQL学习建议1.1、为什么学习 MySQL?1.2、…...
逻辑回归简单案例分析--鸢尾花数据集
文章目录 1. IRIS数据集介绍2. 具体步骤2.1 手动将数据转化为numpy矩阵2.1.1 从csv文件数据构建Numpy数据2.1.2 模型的搭建与训练2.1.3 分类器评估2.1.4 分类器的分类报告总结2.1.5 用交叉验证(Cross Validation)来验证分类器性能2.1.6 完整代码…...

Python print 高阶玩法
Python print 高阶玩法 当涉及到在Python中使用print函数时,有许多方式可以玩转文本样式、字体和颜色。在此将深入探讨这些主题,并介绍一些print函数的高级用法。 1. 基本的文本样式与颜色设置 使用ANSI转义码 ANSI转义码是一种用于在终端࿰…...
Wpf 使用 Prism 实战开发Day09
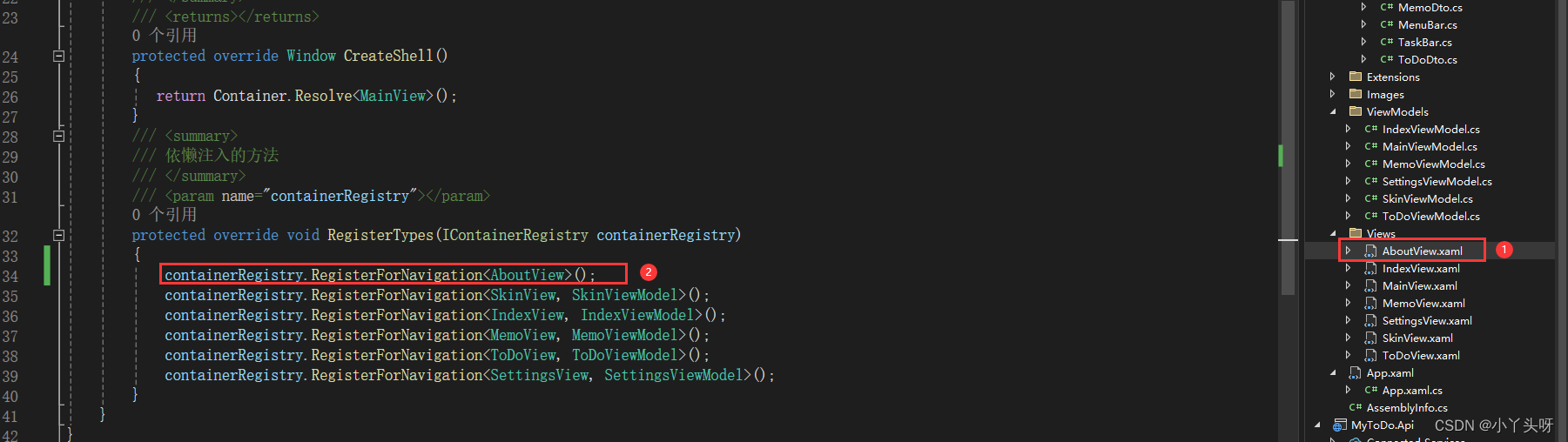
设置模块设计 1.效果图 一.系统设置模块,主要有个性化(用于更改主题颜色),系统设置,关于更多,3个功能点。 个性化的颜色内容样式,主要是从 Material Design Themes UI简称md、提供的demo里复制代码过来使用的。 1.设置…...
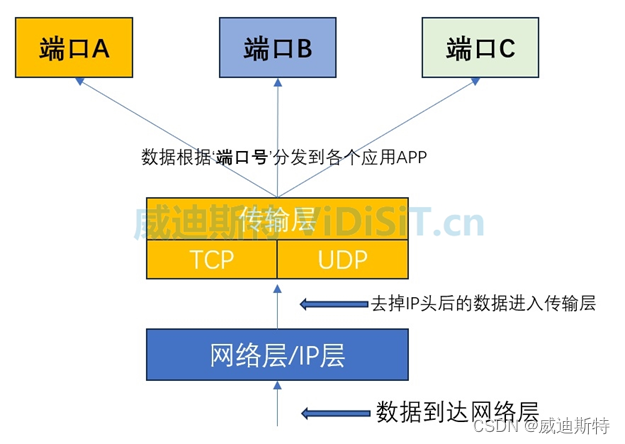
网络端口(包括TCP端口和UDP端口)的作用、定义、分类,以及在视频监控和流媒体通信中的定义
目 录 一、什么地方会用到网络端口? 二、端口的定义和作用 (一)TCP协议和UDP协议 (二)端口的定义 (三)在TCP/IP体系中,端口(TCP和UDP)的作用 (…...

flink如何写入es
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、写入到Elasticsearch5二、写入到Elasticsearch7总结 前言 Flink sink 流数据写入到es5和es7的简单示例。 一、写入到Elasticsearch5 pom maven依赖 <d…...

Java、Python、C++和C#的界面开发框架和工具的重新介绍
好的,以下是Java、Python、C和C#的界面开发框架和工具的重新介绍: Java界面开发: Swing: 是Java提供的一个基于组件的GUI工具包,可以创建跨平台的图形用户界面。它提供了丰富的组件和布局管理器,使得界面开发相对简单。…...

Java二叉树的遍历以及最大深度问题
Java学习面试指南:https://javaxiaobear.cn 1、树的相关概念 1、树的基本定义 树是我们计算机中非常重要的一种数据结构,同时使用树这种数据结构,可以描述现实生活中的很多事物,例如家谱、单位的组织架构、等等。 树是由n&#…...
Apollo 9.0搭建问题记录
虚拟机安装 可以看这个:https://blog.csdn.net/qq_45138078/article/details/129815408 写的很详细 内存 为了学习 Apollo ,所以只是使用了虚拟机,内存得大一点(128G),第一次,就是因为分配内…...

【心得】PHP文件包含高级利用攻击面个人笔记
目录 一、nginx日志文件包含 二、临时文件包含 三、php的session文件包含 四、pear文件包含 五 、远程文件包含 文件包含 include "/var/www/html/flag.php"; 一 文件名可控 $file$_GET[file]; include $file.".php"; //用php伪协议 ࿰…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
