悟的复杂度分析
复杂度分析:
时间复杂度(算法中的基本操作的执行次数);
空间复杂度。
时间复杂度:
实际上我们计算时间复杂度时,我们其实并不需要计算准确的执行次数,只需要大概的执行次数,因此我们在这里使用大O的渐进表示法。常见的时间复杂度O(1), O(N²), O(N), O(logN)。
大O符号:
是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1.用常数1取代运行时间中的所有加法常数;
例:
计算下面代码的时间复杂度
void f(int N)
{int count = 0;for(int k = 0; k < 100; ++k){++count;}
}答案:O(1)
注:确定的常数次,都是O(1)。
2.在修改后的运行次数函数中,只保留最高阶项;
例:
计算下面代码的时间复杂度
void f(int N)
{int count = 0;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){++count;}}for (int k = 0; k < 2 * N; k++){count++;}int M = 10;while (M--){++count;}printf("%d", count);
}答案:O(N²)
注:准确的执行次数:N² + 2 * N + 10
随着N的增大,这个表达式中N²对结果的影响最大
3.若最高阶项存在且不是1,则去除与这个项相乘的常数。得到的结果就是大O阶。
例:
计算下面代码的时间复杂度
void f(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){count++;}int M = 10;while (M--){++count;}printf("%d", count);
}答案:O(N)
特殊情况:
例一:
计算下面代码的时间复杂度
void f(int N, int M)
{int count = 0;for (int k = 0; k < N; k++){++count;}for (int k = 0; k < M; k++){++count;}
}答案:O(M + N)
注:假如给了条件:M远大于N,答案是O(M);M和N差不多大,O(M)或O(N)。
例二:
计算下面代码的时间复杂度
const char* s(const char* str, char cha)
{while (*str != '\0'){if (*str == cha){return str;}++str;}return NULL;
}假设字符串长度是N。
答案:O(N)
注:有些算法的时间复杂度存在最好,平均,最坏情况:
最坏:O(N)
平均:O(N/2)
最好:O(1)
在实际中一般情况关注的是算法的最坏运行情况。
例三:
计算下面代码的时间复杂度
void B(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (!exchange){break;}}
}答案:O(N²)
注:第一趟冒泡:N
第二趟冒泡:N - 1
........
第N趟:1
以上是个等差数列,所以准确的次数是(N+1)*N/2
时间复杂度为O(N²)
例四:
计算下面代码的时间复杂度
int B(int* a, int n, int x)
{assert(a);int begin = 0;int end = n;while (begin < end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x){begin = mid + 1;}else if (a[mid] > x){end = mid;}else{return mid;}}return - 1;
}答案:O(logN)
注:假设找了X次
2的X的平方 = N
X=logN
因为有很多地方不好写底数,所以一般省略简写成logN。
例五:
计算下面代码的时间复杂度
long long f(size_t N)
{return N < 2 ? N : f(N - 1) * N;
}答案:O(N²)
注:递归调用了N次,每次递归运算--》O(1)
整体就是O(N)。
相关文章:

悟的复杂度分析
复杂度分析: 时间复杂度(算法中的基本操作的执行次数); 空间复杂度。 时间复杂度: 实际上我们计算时间复杂度时,我们其实并不需要计算准确的执行次数,只需要大概的执行次数,因此我们…...
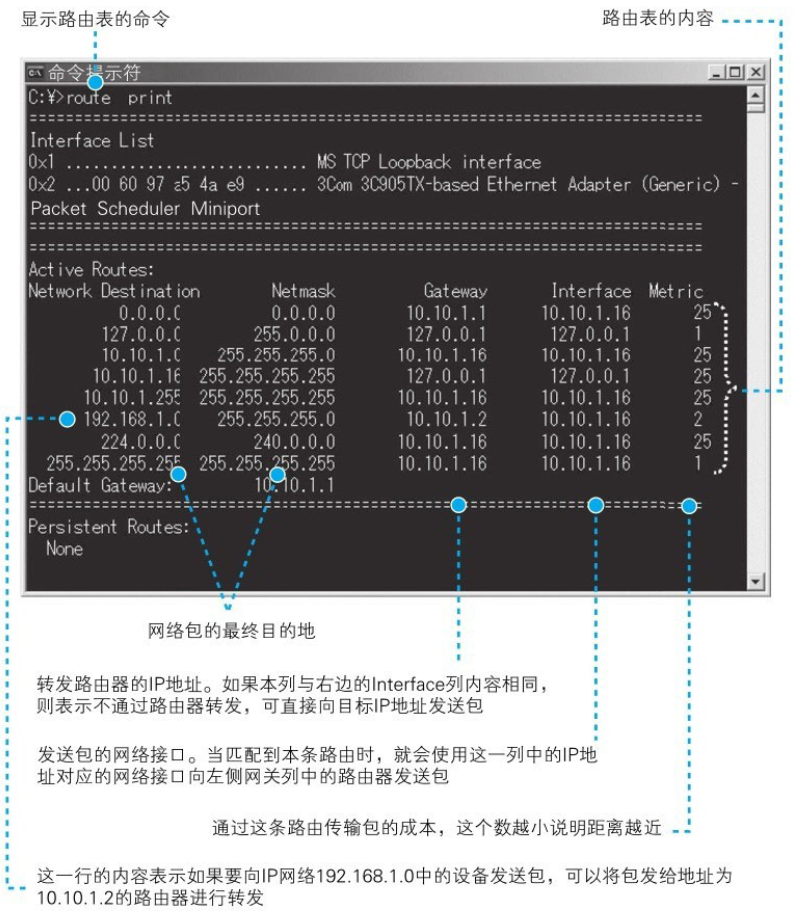
《网络是怎样连接的》2.5节图表(自用)
图5.1:ip包结构 图5.2:ip网络包的传输方式 1.以太网的部分也可以替换成其他的东西,例如无线局域网、ADSL、FTTH等,它们都可以替代以太网的角色帮助IP协议来传输网络包 2.根据ARP协议,客户端可以根据ip地址得到下一个路…...
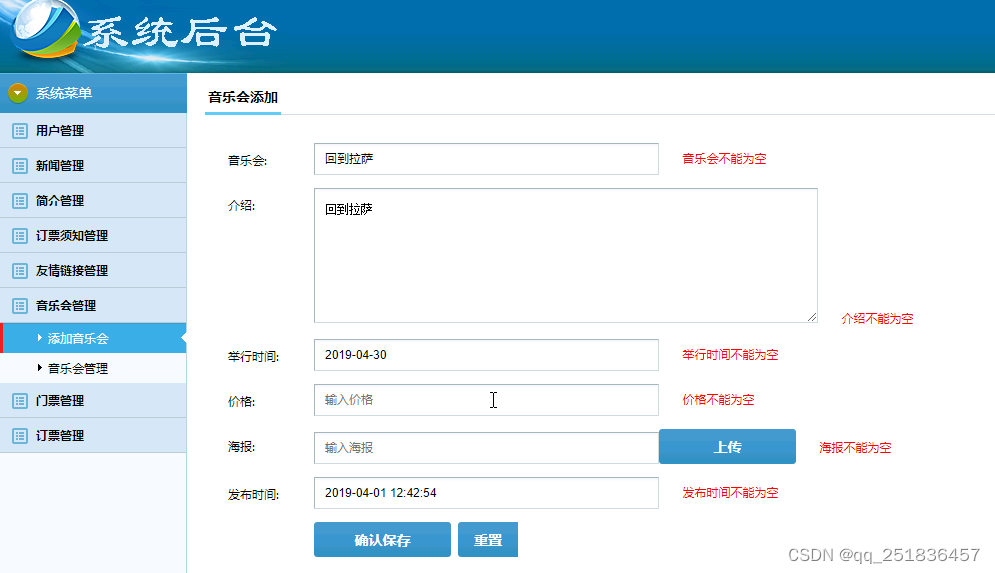
java 音乐会售票平台系统Myeclipse开发mysql数据库struts2结构java编程计算机网页项目
一、源码特点 java 音乐会售票平台系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助struts2框架开发mvc模式,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发 环境为TOCAT7.0,Myeclipse8.5开发,数据…...
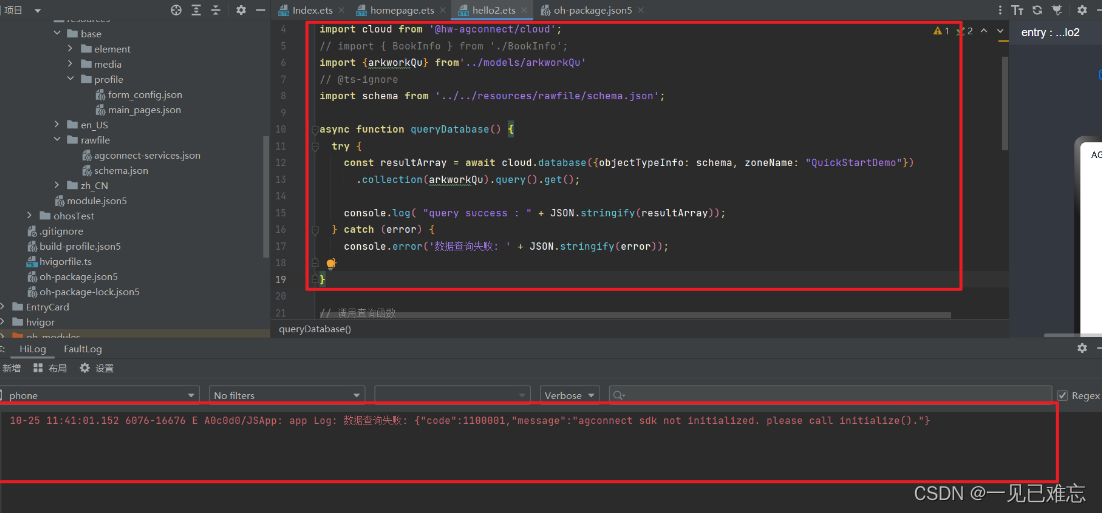
鸿蒙开发解决agconnect sdk not initialized. please call initialize()
文章目录 项目场景:问题描述原因分析:解决方案:总结:项目场景: 鸿蒙开发报错: agconnect sdk not initialized. please call initialize() 问题描述 报错内容为: 10-25 11:41:01.152 6076-16676 E A0c0d0/JSApp: app Log: 数据查询失败: {“code”:1100001,“messag…...

秋招阿里巴巴java笔试试题-精
一、单项选择题 1、以下函数的时间复杂度是 ( ) 1 2 3 4 5 6 7 8 9 void func(int x,int y, int z){ if(x<0) printf("%d, %d\n", y, z); else { func(x-1,y1,z); func(x-1,y,z1); } } A.O(x*y*z) B.O(x^2*y^2) C.O(2^x) D.O(2^x*…...

018、通用集合类型
Rust标准库包含了一系列非常有用的被称为集合的数据结构。大部分的数据结构都代表着某个特定的值,但集合却可以包含多个值。 与内置的数组与元组类型不同,这些集合将自己持有的数据存储在了堆上。这意味着数据的大小不需要在编译时确定,并且可…...
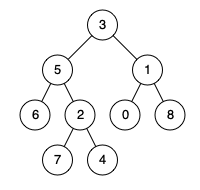
【Leetcode】236.二叉树的最近公共祖先
一、题目 1、题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。” 示例1…...
C#,入门教程(11)——枚举(Enum)的基础知识和高级应用
上一篇: C#,入门教程(10)——常量、变量与命名规则的基础知识https://blog.csdn.net/beijinghorn/article/details/123913570 不会枚举,就不会编程! 枚举 一个有组织的常量系列 比如:一个星期每一天的名字…...
java SSM水质历史数据可视化设计myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM水质历史数据可视化设计是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主…...

C++推箱子游戏开发
游戏 自动地图生成背景音乐推箱子到目标位置 美工资源 美工资源: 链接:https://pan.baidu.com/s/1MZv8pDBXdNDbXxuAAPSM-A **提取码:**2syq 图形库: www.easyx.cn cpp文件 #include "box_man.h" #include <conio.h> #…...

Kotlin函数式接口
函数式接口 接口只有一个抽象方法的接口,称为 函数式接口 functional interface,也叫做 Single Abstract Method(SAM) interface。 注:函数式接口,只有一个抽象方法,但可以有多个非抽象方法。 一、Kotlin Kotlin支持…...

2024年1月9日学习总结
目录 学习目标学习内容联邦学习基础:why, what, howwhy?what?how? 联邦学习的例子——CIFAR-10数据集(分类问题)1、import libararies2、hyper-parameters3、加载并且划分数据4、创建神经网络模型5、helper…...

Nacos使用MySQL8时区问题导致启动失败
文章目录 配置下mysql的时区方式一 (永久)方式二(临时) 由于mysql8需要配置时区,如果不配置时区,nacos就连不上mysql,从而也就无法登录nacos自带的图形化界面 配置下mysql的时区 方式一 (永久) 直接修改配置文件&…...
在k8s集群中部署多nginx-ingress
关于ingress的介绍,前面已经详细讲过了,参考ingress-nginx详解和部署方案。本案例ingress的部署使用deploymentLB的方式。 参考链接: 多个ingress部署 文章目录 1. 下载ingress的文件2. 文件资源分析3. 部署ingress3.1 部署第一套ingress3.1…...

SLF4J Spring Boot日志框架
JAVA日志框架 JAVA有好多优秀的日志框架,比如log4j、log4j2、logback、JUL(java.util.logging)、JCL(JAVA Common Logging)等等,logback是后起之秀,是Spring Boot默认日志框架。 今天文章的目…...

mysql之导入导出远程备份
文章目录 一、navicat导入导出二、mysqldump命令导入导出2.1导出2.1.1 导出表数据和表结构2.1.2 只导出表结构() 2.2 导入(使用mysqldump导入 包含t _log表的整个数据库 共耗时 20s;)方法一:方法二: 三、LOAD DATA INFILE命令导入导出(只针对单表)设置导…...

Java虚拟机ART 读书笔记 第2章 深入理解Class文件格式
GitHub - Omooo/Android-Notes: ✨✨✨这有一包小鱼干,确定不要吃嘛?( 逃 深入理解Android:Java虚拟机ART 读书笔记 以下内容均来自书中内容 建议看原书哦 第2章 深入理解Class文件格式 2.1 class文件总览 Class文件格式全貌 u4ÿ…...

编程基础 - 初识Linux
编程基础 - 初识Linux 返回序言及专栏目录 文章目录 编程基础 - 初识Linux前言一、Linux发展简介二、现代Linux三、Linux系统各发行版小结 前言 为什么要学习Linux呢?我这Windows用得好好的,简单易用傻瓜式、用的人还超多!但是我要告诉你的…...

c yuv422转yuv420p
思路: yuv422 存储格式为 y u y v y u y v y u y v y u y v yuv420p 存储最简单,先存所以的y,再存u,最后v 所以先把422所有的y存在一起,再提奇数行的u ,偶数行舍弃。提…...
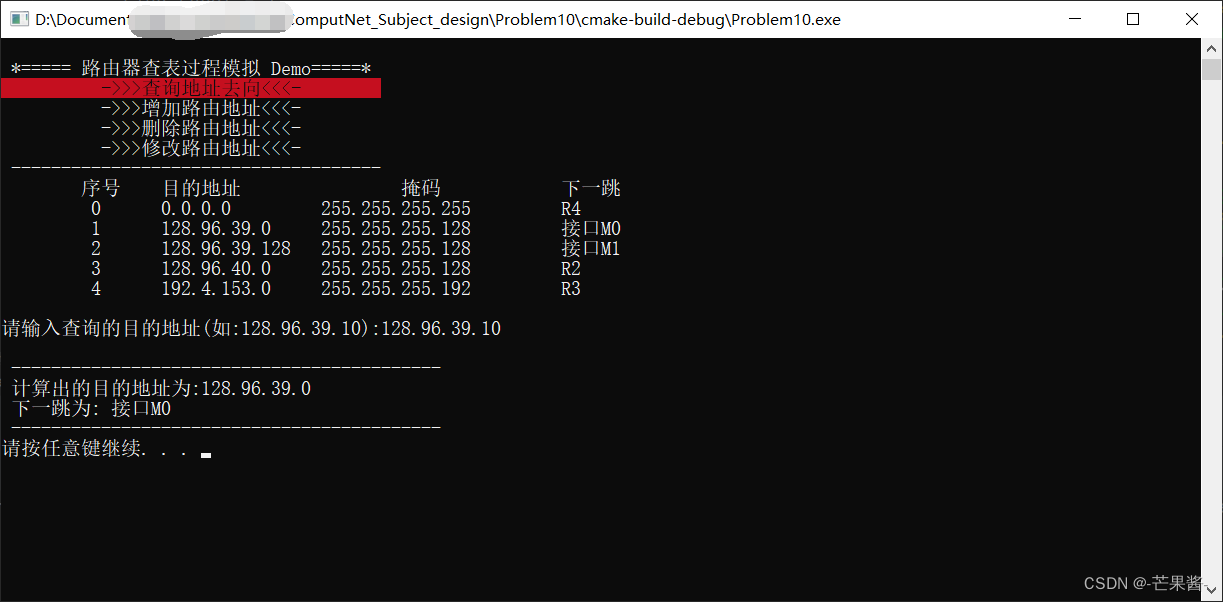
计算机网络 - 路由器查表过程模拟 C++(2024)
1.题目描述 参考计算机网络教材 140 页 4.3 节内容,编程模拟路由器查找路由表的过程,用(目的地址 掩码 下一跳) 的 IP 路由表以及目的地址作为输入,为目的地址查找路由表,找出正确的下一跳并输出结果。 1.…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
