算法训练day9Leetcode232用栈实现队列225用队列实现栈
今天学习的文章和视频链接
https://programmercarl.com/%E6%A0%88%E4%B8%8E%E9%98%9F%E5%88%97%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
栈与队列理论基础
见我的博客 https://blog.csdn.net/qq_36372352/article/details/135470438?spm=1001.2014.3001.5501
232用栈实现队列
题目描述
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):实现 MyQueue 类:void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。示例 1:输入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false提示:1 <= x <= 9
最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)进阶:你能否实现每个操作均摊时间复杂度为 O(1) 的队列?换句话说,执行 n 个操作的总时间复杂度为 O(n) ,即使其中一个操作可能花费较长时间。
题目分析
在push数据的时候,只要数据放进输入栈就好,但在pop的时候,操作就复杂一些,输出栈如果为空,就把进栈数据全部导入进来(注意是全部导入),再从出栈弹出数据,如果输出栈不为空,则直接从出栈弹出数据就可以了。
最后如何判断队列为空呢?如果进栈和出栈都为空的话,说明模拟的队列为空了。
在代码实现的时候,会发现pop() 和 peek()两个函数功能类似,代码实现上也是类似的,可以思考一下如何把代码抽象一下。
acm模式代码
#include <iostream>
#include <queue>
#include <stack>class MyQueue {
public:std::stack<int> stIn;std::stack<int> stOut; MyQueue() {}void push(int x) {stIn.push(x);}int pop() {// 只有当stOut为空的时候,再从stIn里导入数据(导入stIn全部数据)if (stOut.empty()) {while (!stIn.empty()) {stOut.push(stIn.top());stIn.pop();}}int result = stOut.top();stOut.pop();return result;}int peek() {int res = this->pop();stOut.push(res);return res;}bool empty() {return stIn.empty() && stOut.empty();}
};/*** Your MyQueue object will be instantiated and called as such:* MyQueue* obj = new MyQueue();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->peek();* bool param_4 = obj->empty();*/int main() {MyQueue* queue = new MyQueue();queue->push(1);queue->push(2);std::cout << queue->peek() << std::endl; // 输出 1std::cout << queue->pop() << std::endl; // 输出 1std::cout << (queue->empty() ? "true" : "false") << std::endl; // 输出 falsedelete queue; // Don't forget to free the allocated memory}
peek()的实现,直接复用了pop(), 要不然,对stOut判空的逻辑又要重写一遍。
再多说一些代码开发上的习惯问题,在工业级别代码开发中,最忌讳的就是 实现一个类似的函数,直接把代码粘过来改一改就完事了。
这样的项目代码会越来越乱,一定要懂得复用,功能相近的函数要抽象出来,不要大量的复制粘贴,很容易出问题!
255 用队列实现栈
题目描述
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。实现 MyStack 类:void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。注意:你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
我看完题目后的想法
用两个队列,一个队列存一个数便马上弹出到另一个队列
题目分析
一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时再去弹出元素就是栈的顺序了。只需要一个队列就可以实现。
acm模式代码
#include <iostream>
#include <queue>class MyStack {
public:std::queue<int> qe;MyStack() {}void push(int x) {qe.push(x);}int pop() {int n = qe.size() - 1;while (n--) {qe.push(qe.front());qe.pop();}int res = qe.front();qe.pop();return res;}int top() {return qe.back();}bool empty() {return qe.empty();}
};int main() {MyStack stack;stack.push(1);stack.push(2);std::cout << stack.pop() << std::endl; // 输出 2std::cout << (stack.empty() ? "true" : "false") << std::endl; // 输出 false
}/*** Your MyStack object will be instantiated and called as such:* MyStack* obj = new MyStack();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->top();* bool param_4 = obj->empty();*/
相关文章:

算法训练day9Leetcode232用栈实现队列225用队列实现栈
今天学习的文章和视频链接 https://programmercarl.com/%E6%A0%88%E4%B8%8E%E9%98%9F%E5%88%97%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 栈与队列理论基础 见我的博客 https://blog.csdn.net/qq_36372352/article/details/135470438?spm1001.2014.3001.5501 232用栈实现…...
linux驱动(四):platform
本文主要探讨x210驱动的平台设备类型(platform)以及misc设备。 驱动模型 设备驱动模型:总线(bus type)、设备(device)和驱动(driver) 总线:虚拟总线用于挂接驱动驱动和设备 总线、设备、驱动关系:/sys/bus下的子目录…...
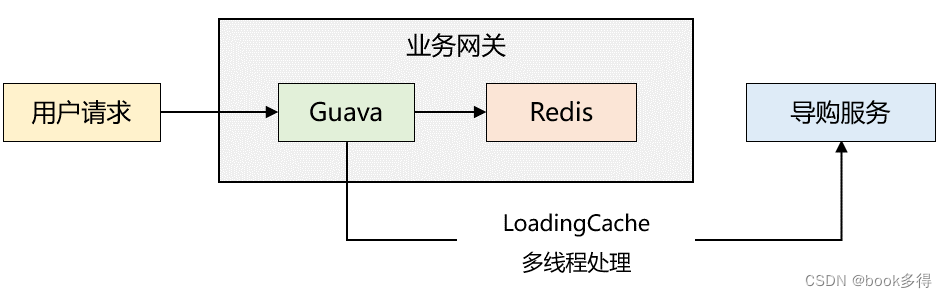
Guava:Cache强大的本地缓存框架
Guava Cache是一款非常优秀的本地缓存框架。 一、 经典配置 Guava Cache 的数据结构跟 JDK1.7 的 ConcurrentHashMap 类似,提供了基于时间、容量、引用三种回收策略,以及自动加载、访问统计等功能。 基本的配置 Testpublic void testLoadingCache() th…...

#{}和${}的区别?
#{}是占位符,预编译处理;${}是拼接符,字符串替换,没有预编译处理。Mybatis在处理#{}时,#{}传入参数是以字符串传入,会将SQL中的#{}替换为?号,调用PreparedStatement的set方法来赋值。Mybatis在…...

string的模拟实现
string的模拟实现 msvc和g下的string内存比较成员变量构造函数与析构函数拷贝构造函数赋值拷贝c_str、size和capacity函数以及重载[]、clear、expand_capacity迭代器与遍历reservepush_back、append、insert字符串比较运算符erase<<流提取 >>流插入resizefindsubst…...

算法练习:查找二维数组中的目标值
题目: 编写一个高效的算法来搜索矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:每行的元素从左到右升序排列。每列的元素从上到下升序排列。 实现: 1. main方法 public static void main(String[] args) {int[][] matrix {{1…...

考研自命题资料、考题如何找
这篇文章是抖音和b站上上传的同名视频的原文稿件,感兴趣的csdn用户可以关注我的抖音和b站账号(GeekPower极客力量)。同时这篇文章也为视频观众提供方便,可以更加冷静地分析和思考。文章同时在知乎发表。 去年我发布了一个视频&am…...
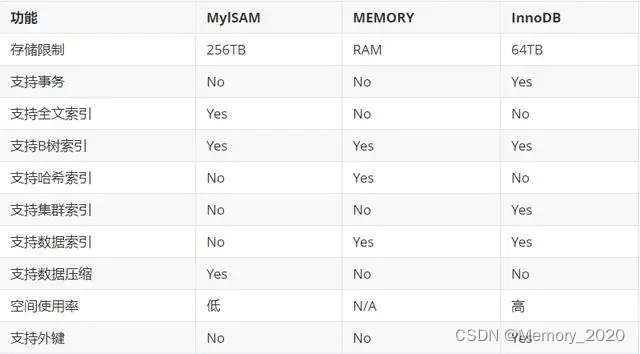
MySQL 存储引擎和索引类型介绍
1. 引言 MySQL 是一个流行的关系型数据库管理系统,提供多种存储引擎以满足不同的业务需求。本文将介绍几种常见的 MySQL 存储引擎和索引类型比较,并给出相应的示例。 2. 存储引擎概述 2.1 InnoDB 存储引擎 InnoDB 是 MySQL 的默认存储引擎࿰…...
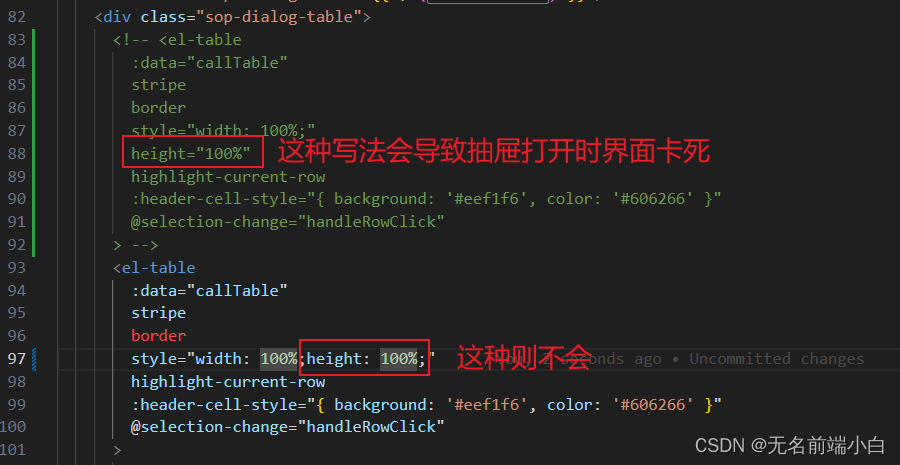
element-ui table height 属性导致界面卡死
问题: 项目上,有个点击按钮弹出抽屉的交互, 此时界面卡死 原因分析: 一些场景下(父组件使用动态单位/弹窗、抽屉中使用), element-ui 的 table 会循环计算高度值, 导致界面卡死 github 上的一些 issues 和解决方案: Issues ElemeFE/element GitHub 官方讲是升…...
Vue2.v-指令
v-if 在双引号中写判断条件。 <div v-if"score>90">A</div> <div v-else-if"score>80">B</div> <div v-else>C</div>v-on: :冒号后面跟着事件。 为了简化,可以直接用代替v-on:。 事件名“内联语…...
Java中SpringBoot组件集成接入【Knife4j接口文档(swagger增强)】
Java中SpringBoot组件集成接入【Knife4j接口文档】 1.Knife4j介绍2.maven依赖3.配置类4.常用注解使用1.实体类及属性(@ApiModel和@ApiModelProperty)2.控制类及方法(@Api、@ApiOperation、@ApiImplicitParam、 @ApiResponses)3.@ApiOperationSupport注解未生效的解决方法5.…...
继承和多态的详解
文章目录 1. 继承1.1 继承的概念1.3 继承的语法1.3 父类成员访问1.3.1 子类中访问父类的成员变量1.3.2 子类中访问父类的成员方法 1.4 子类构造方法 2.super关键字2.1 super关键字的概念2.2 super和this的区别 3. 在继承中访问限定符的可见性4. 继承方式的分类5. 多态5.1 多态的…...
快速上手)
【Unity】UniTask(异步工具)快速上手
UniTask(异步工具) 官方文档:https://github.com/Cysharp/UniTask/blob/master/README_CN.md URL:https://github.com/Cysharp/UniTask.git?pathsrc/UniTask/Assets/Plugins/UniTask 优点:0GC,可以在任何地方使用 为Unity提供一个高性能&…...

k8s三种常用的项目发布方式
k8s三种常用的项目发布方式 1、 蓝绿发布 2、 金丝雀发布(灰度发布):使用最多 3 、滚动发布 应用程序升级,面临的最大问题是新旧业务之间的切换。 项目的生命周期:立项----定稿----需求发布----开发----测试-----发布 最后测试之后上线。再…...

Nodejs搭配axios下载图片
新建一个文件夹,npm i axios 实测发现只需保留node_modules文件夹,删除package.json不影响使用 1.纯下载图片 其实该方法不仅可以下载图片,其他的文件都可以下载 const axios require(axios) const fs require(fs) var arrPic [https:…...
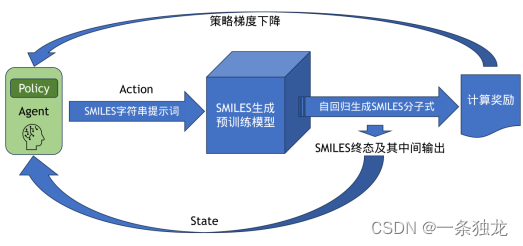
强化学习在生成式预训练语言模型中的研究现状简单调研
1. 绪论 本文旨在深入探讨强化学习在生成式预训练语言模型中的应用,特别是在对齐优化、提示词优化和经验记忆增强提示词等方面的具体实践。通过对现有研究的综述,我们将揭示强化学习在提高生成式语言模型性能和人类对话交互的关键作用。虽然这些应用展示…...

python_selenium_安装基础学习
目录 1.为什么使用selenium 2.安装selenium 2.1Chrome浏览器 2.2驱动 2.3下载selenium 2.4测试连接 3.selenium元素定位 3.1根据id来找到对象 3.2根据标签属性的属性值来获取对象 3.3根据xpath语句来获取对象 3.4根据标签的名字获取对象 3.5使用bs4的语法来获取对象…...
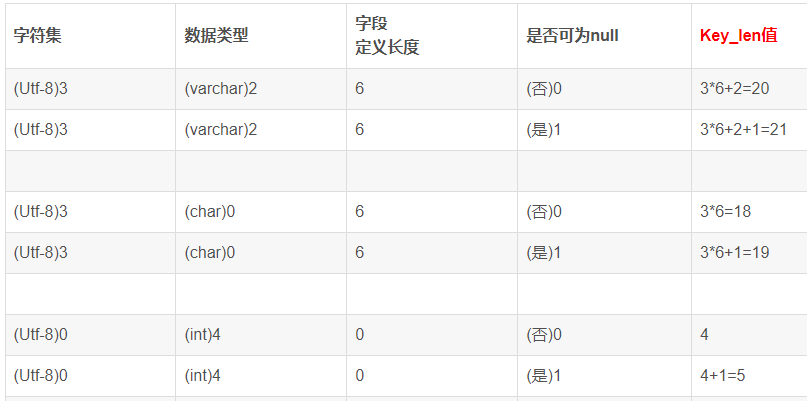
面试宝典进阶之关系型数据库面试题
D1、【初级】你都使用过哪些数据库? (1)MySQL:开源数据库,被Oracle公司收购 (2)Oracle:Oracle公司 (3)SQL Server:微软公司 (4&#…...

Agisoft Metashape 地面点分类参数设置
Agisoft Metashape 点云分类之地面点分类参数设置 文章目录 Agisoft Metashape 点云分类之地面点分类参数设置前言一、分类地面点参数二、农村及城区有房屋地区二、植被区域分类三、侵蚀半径(Erosion radius)参数设置前言 Agisoft Metashape提供了自动检测地面点的功能,减少…...

计算机科学速成课【学习笔记】(4)——二进制
本集课程B站链接: 4. 二进制-Representing Numbers and Letters with Binary_BiliBili_哔哩哔哩_bilibili4. 二进制-Representing Numbers and Letters with Binary_BiliBili是【计算机科学速成课】[40集全/精校] - Crash Course Computer Science的第4集视频&…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
)
RMQ 算法详解(区间最值问题)
RMQ 算法详解(区间最值问题) 问题介绍解决方法暴力法ST表法基本思想算法步骤C实现 问题介绍 RMQ问题是OI中经常遇到的问题,主要是一下形式: 给你一堆数,不断的对里面的数进行操作,例如:让某个…...
