CEC2020:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2020(提供MATLAB代码
一、鱼鹰优化算法简介
鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovský于2023年提出,其模拟鱼鹰的捕食行为。

鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米,体重1000-1750克。头部白色,头顶具有黑褐色的纵纹,枕部的羽毛稍微呈披针形延长,形成一个短的羽冠。头的侧面有一条宽阔的黑带,从前额的基部经过眼睛到后颈部,并与后颈的黑色融为一体。上体为暗褐色,略微具有紫色的光泽。下体为白色,胸部的暗色纵纹和飞羽,以及尾羽上相间排列的横斑均极为醒目。虹膜淡黄色或橙黄色,眼周裸露皮肤铅黄绿色,嘴黑色,蜡膜铅蓝色,脚和趾黄色,爪黑色。
鱼鹰栖息于湖泊、河流、海岸或开阔地,尤其喜欢在山地森林中的河谷或有树木的水域地带活动。常见在江河、湖沼及海滨一带飞翔,一见水中有饵,就直下水面,用脚掠之而去。趾具锐爪,趾底遍生细刺,外趾复能由前向后反转,这些都很适于捕鱼。在天气晴朗之日,盘旋于水面上空,定点后俯冲而下,再将捕获的鱼带至岩石、电杆、树上等地方享用。巢常营于海岸或岛屿的岩礁上。主要以鱼为食,有时也捕食蛙、蜥蜴、小型鸟类等其他小型陆栖动物。除了南极和北极,亚洲、北美洲等各大洲均有分布。
1.1鱼鹰优化算法原理
鱼鹰优化算法包含两个阶段:第一阶段为鱼鹰识别鱼的位置并捕鱼(全局勘探), 第二阶段为将鱼带到合适的位置( 局部开采),其详细设计如下:
1.1.1 种群初始化
采用下式随机初始化鱼鹰种群:
X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,j⋯x1,m⋮⋱⋮⋱⋮xi,1⋯xi,j⋯xi,m⋮⋱⋮⋱⋮xN,1⋯xN,j⋯xN,m]N×m,xi,j=lbj+ri,j⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,\begin{array}{c} X=\left[\begin{array}{c} X_{1} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N} \end{array}\right]_{N \times m}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m}, \\ x_{i, j}=l b_{j}+r_{i, j} \cdot\left(u b_{j}-l b_{j}\right), i=1,2, \ldots, N, j=1,2, \ldots, m, \end{array}X=X1⋮Xi⋮XNN×m=x1,1⋮xi,1⋮xN,1⋯⋱⋯⋱⋯x1,j⋮xi,j⋮xN,j⋯⋱⋯⋱⋯x1,m⋮xi,m⋮xN,mN×m,xi,j=lbj+ri,j⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,
其中,N为鱼鹰的数量,m为问题的维度,初始化位置后依据优化问题计算适应度值:
F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1F=\left[\begin{array}{c} F_{1} \\ \vdots \\ F_{i} \\ \vdots \\ F_{N} \end{array}\right]_{N \times 1}=\left[\begin{array}{c} F\left(X_{1}\right) \\ \vdots \\ F\left(X_{i}\right) \\ \vdots \\ F\left(X_{N}\right) \end{array}\right]_{N \times 1}F=F1⋮Fi⋮FNN×1=F(X1)⋮F(Xi)⋮F(XN)N×1
1.1.2 全局勘探(第一阶段:位置识别和捕鱼)
鱼鹰是强大的猎人,由于其强大的视力,能够探测到水下鱼类的位置。在确定鱼的位置后,他们攻击它并通过潜入水下捕猎鱼。OOA中种群更新的第一阶段是基于对鱼鹰这种自然行为的模拟而建模的。对鱼鹰攻击鱼类进行建模会导致鱼鹰在搜索空间中的位置发生显著变化,这增加了OOA在识别最优区域和逃离局部最优方面的探索能力。在OOA设计中,对于每只鱼鹰,搜索空间中具有较好目标函数值的其他鱼鹰的位置被视为水下鱼类。每只鱼鹰的位置使用下式指定。
FPi={Xk∣k∈{1,2,…,N}∧Fk<Fi}∪{Xbest }\boldsymbol{F P _ { i }}=\left\{X_{k} \mid \boldsymbol{k} \in\{1,2, \ldots, N\} \wedge \boldsymbol{F}_{k}<\boldsymbol{F}_{i}\right\} \cup\left\{\boldsymbol{X}_{\text {best }}\right\}FPi={Xk∣k∈{1,2,…,N}∧Fk<Fi}∪{Xbest }
其中,FPiF P _ { i }FPi为第i只鱼鹰的位置集合,Xbest {X}_{\text {best }}Xbest 为最佳鱼鹰的位置。
鱼鹰随机检测其中一条鱼的位置并攻击它。基于鱼鹰向鱼的运动模拟,使用下式计算相应鱼鹰的新位置。这个新位置,如果它的目标函数的值更好,则替换鱼鹰的先前位置。
xi,jP1=xi,j+ri,j⋅(SFi,j−Ii,j⋅xi,j),xi,jP1={xi,jP1,lbj≤xi,jP1≤ubj;lbj,xi,jP1<lbj;ubj,xi,jP1>ubj.Xi={XiP1,FiP1<Fi;Xi,else ,\begin{array}{l} x_{i, j}^{P 1}=x_{i, j}+r_{i, j} \cdot\left(S F_{i, j}-I_{i, j} \cdot x_{i, j}\right), \\ x_{i, j}^{P 1}=\left\{\begin{array}{ll} x_{i, j}^{P 1}, & l b_{j} \leq x_{i, j}^{P 1} \leq u b_{j} ; \\ l b_{j}, & x_{i, j}^{P 1}<l b_{j} ; \\ u b_{j}, & x_{i, j}^{P 1}>u b_{j} . \end{array}\right. \\ X_{i}=\left\{\begin{array}{l} X_{i}^{P 1}, F_{i}^{P 1}<F_{i} ; \\ X_{i}, \text { else }, \end{array}\right. \\ \end{array}xi,jP1=xi,j+ri,j⋅(SFi,j−Ii,j⋅xi,j),xi,jP1=⎩⎨⎧xi,jP1,lbj,ubj,lbj≤xi,jP1≤ubj;xi,jP1<lbj;xi,jP1>ubj.Xi={XiP1,FiP1<Fi;Xi, else ,
其中,xi,jP1x_{i, j}^{P 1}xi,jP1为第i只鱼鹰在第一阶段时,其第j维的新位置,Fi,jP1F_{i, j}^{P 1}Fi,jP1是其对应的适应度值。SFi,jS F_{i, j}SFi,j为[0,1]之间的随机数,Ii,jI_{i, j}Ii,j为集合{1,2}中的随机数。
1.1.3 局部开采(第二阶段:将鱼带到合适的位置)
捕食鱼后,鱼鹰将其带到合适(对他来说安全)的位置,并在那里吃。OOA中更新种群的第二阶段是基于鱼鹰这种自然行为的模拟建模的。将鱼带到合适位置的建模导致鱼鹰在搜索空间中的位置发生微小变化,从而导致 OOA 在本地搜索中的开发能力增加,并在发现的解决方案附近收敛到更好的解决方案。在OOA的设计中,为了模拟鱼鹰的这种自然行为,首先,针对种群的每个成员,使用下式计算一个新的随机位置作为“适合吃鱼的位置”。然后,如果目标函数的值在这个新位置得到改善,则替换相应鱼鹰的先前位置。
xi,jP2=xi,j+lbj+r⋅(ubj−lbj)t,i=1,2,…,N,j=1,2,…,m,t=1,2,…,T,xi,jP2={xi,jP2,lbj≤xi,jP2≤ubj;lbj,xi,jP2<lbjubj,xi,jP2>ubj,Xi={XiP2,FiP2<Fi;Xi,else ,\begin{array}{c} x_{i, j}^{P 2}=x_{i, j}+\frac{l b_{j}+r \cdot\left(u b_{j}-l b_{j}\right)}{t}, i=1,2, \ldots, N, j=1,2, \ldots, m, t=1,2, \ldots, T, \\ x_{i, j}^{P 2}=\left\{\begin{array}{l} x_{i, j}^{P 2}, l b_{j} \leq x_{i, j}^{P 2} \leq u b_{j} ; \\ l b_{j}, x_{i, j}^{P 2}<l b_{j} \\ u b_{j}, x_{i, j}^{P 2}>u b_{j}, \end{array}\right. \\ X_{i}=\left\{\begin{array}{l} X_{i}^{P 2}, F_{i}^{P 2}<F_{i} ; \\ X_{i}, \text { else }, \end{array}\right. \end{array}xi,jP2=xi,j+tlbj+r⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,t=1,2,…,T,xi,jP2=⎩⎨⎧xi,jP2,lbj≤xi,jP2≤ubj;lbj,xi,jP2<lbjubj,xi,jP2>ubj,Xi={XiP2,FiP2<Fi;Xi, else ,
其中,xi,jP2x_{i, j}^{P 2}xi,jP2为第i只鱼鹰在第二阶段时,其第j维的新位置,Fi,jP2F_{i, j}^{P 2}Fi,jP2是其对应的适应度值。rrr为[0,1]之间的随机数,ttt和TTT分别为当前迭代次数和最大迭代次数。
1.2算法描述

1.3算法流程

1.4参考文献
Dehghani Mohammad, Trojovský Pavel.Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems[J].Frontiers in Mechanical Engineering,2023,8.
二、CEC2020简介
CEC2020共有10个测试函数测试维度包含:2D、5D、10D、15D、20D。CEC2020测试问题随着维度的增加求解极其困难。

三、求解结果
完整代码添加博客下方博主微信:djpcNLP123
将鱼鹰优化算法OOA运用于求解CEC2020中10个函数,其中每个测试函数可以选择的维度分别有:2D、5D、10D、15D、20D。增大迭代次数,鱼鹰优化算法OOA的求解效果更佳。本例测试函数维度均为10D(可根据自己需求调整),种群大小为50,最大迭代次数为100次。
close all
clear
clc
MaxFes = 50;%迭代次数
VarNumber = 10;%维度 2/5/10/15/20
nPop = 50;%种群大小
VarMin=-100;%下限
VarMax=100;%上限
fitnessfunc=str2func('cec20_func');
Function_name=1;%测试函数1-10
[Best_Fit,Best_Pos,Curve]=OOA(nPop,MaxFes,VarMin,VarMax,VarNumber,CostFunction);
figure
plot(Curve,'g','linewidth',2.5)
xlabel('迭代次数')
ylabel('适应度值')
legend('OOA')
title(strcat('CEC2020-F',num2str(Function_name)))部分求解结果:
F1:

F2:

F3:

F4:

F5:

四、参考代码
完整代码添加博客下方博主微信:djpcNLP123
相关文章:

CEC2020:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2020(提供MATLAB代码
一、鱼鹰优化算法简介 鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovsk于2023年提出,其模拟鱼鹰的捕食行为。 鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米…...

词对齐 - MGIZA++
文章目录关于 MGIZAgiza-py安装 MGIZA命令说明mkclsd4normhmmnormplain2sntsnt2coocsnt2coocrmpsnt2plainsymalmgizageneral parameters:No. of iterations:parameter for various heuristics in GIZA for efficient training:parameters for describing the type and amount o…...
GUI 之 Tkinter编程
GUI 图形界面,Tkinter 是 Python 内置的 GUI 库,IDLE 就是 Tkinter 设计的。 1. Tkinter 之初体验 import tkinter as tkroot tk.Tk() # 创建一个窗口root.title(窗口标题)# 添加 label 组件 theLabel tk.Label(root, text文本内容) theLabel.p…...
【软件测试】性能测试面试题都问什么?面试官想要什么?回答惊险避坑......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 1、你认为不同角色关…...

后端开发基础能力以及就Java的主流开发框架介绍
前言:java语言开发转后端,必须了解后端主流的一些东西,共勉。 后端开发需要具备以下基础能力: 1.编程语言:熟练掌握至少一门编程语言,如Java、Python、Ruby、PHP、C#等。 2.数据结构和算法:具…...
H2数据库连接时用户密码错误:Wrong user name or password [28000-214] 28000/28000 (Help)
H2数据库连接时用户密码错误: 2023-03-03 08:25:07 database: wrong user or password; user: "SA" org.h2.message.DbException: Wrong user name or password [28000-214]出现的问题配置信息原因解决办法org.h2.message.DbException: Wrong user name or password …...

青岛诺凯达机械盛装亮相2023济南生物发酵展,3月与您相约
BIO CHINA生物发酵展,作为生物发酵产业一年一度行业盛会,由中国生物发酵产业协会主办,上海信世展览服务有限公司承办,2023第10届国际生物发酵展(济南)于2023年3月30-4月1日在山东国际会展中心(济…...
【JAVA程序设计】【C00111】基于SSM的网上图书商城管理系统——有文档
基于SSM的网上图书商城管理系统——有文档项目简介项目获取开发环境项目技术运行截图项目简介 基于ssm框架开发的网上在线图书售卖商城项目,本项目分为三种权限:系统管理员、卖家、买家 管理员角色包含以下功能: 用户信息管理、权限管理、订…...

基于卷积神经网络CNN的三相故障识别
目录 背影 卷积神经网络CNN的原理 卷积神经网络CNN的定义 卷积神经网络CNN的神经元 卷积神经网络CNN的激活函数 卷积神经网络CNN的传递函数 卷积神经网络CNN手写体识别 基本结构 主要参数 MATALB代码 结果图 展望 背影 现在生活,为节能减排,减少电能损…...

Java工厂设计模式详解,大厂的Java抽象工厂模式分享!
我是好程序员-小源!本期文章主要给大家分享:Java工厂设计模式。文中使用通俗易懂的案例,使你快速学习和轻松上手!一、什么是Java抽象工厂模式1. Java抽象工厂是23种设计模式中创建型模式的一种,Java抽象工厂是由多个工…...

Git 企业级分支提交流程
Git 企业级分支提交流程 首先在本地分支hfdev上进行开发,开发后要经过测试。 如果测试通过了,那么久可以合并到本地分支develop,合并之后hfdev和development应该完全一样。 git add 文件 git commit -m ‘注释’ git checkout develop //切换…...

C/C++每日一练(20230303)
目录 1. 字符串相乘 2. 单词拆分 II 3. 串联所有单词的子串 1. 字符串相乘 给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。 示例 1: 输入: num1 "2", num2 "3"…...
Python3-条件控制
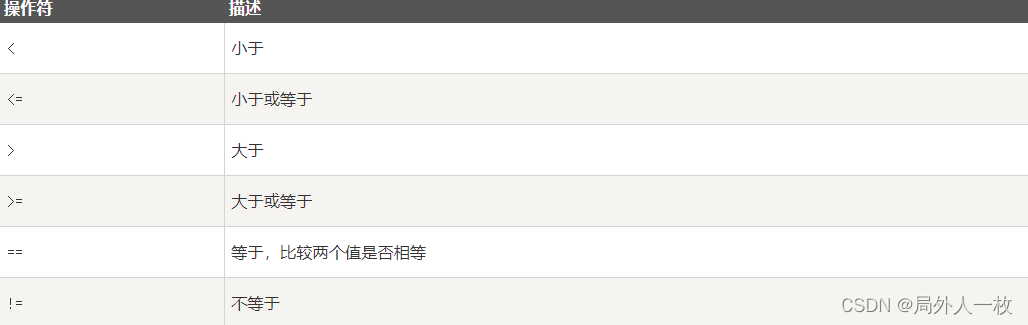
Python3 条件控制 Python 条件语句是通过一条或多条语句的执行结果(True 或者 False)来决定执行的代码块。 可以通过下图来简单了解条件语句的执行过程: 代码执行过程: if 语句 Python中if语句的一般形式如下所示: if condi…...

KDZD地埋电缆故障测试仪
一、产品特性 ★电缆故障测试仪(闪测仪) (1)使用范围广:用于测量各种不同截面、不同介质的各种电力电缆、高频同轴电缆,市话电缆及两根以上均匀铺设的地埋电线等电缆高低阻、短路、开路、断线以及高阻泄漏…...

爆款升级!新系列南卡Neo最强旗舰杀到,业内首款无线充骨传导耳机!
中国专业骨传导耳机品牌NANK南卡于近日发布了全新南卡Neo骨传导运动耳机,打造一款佩戴最舒适、音质体验最好的骨传导耳机。推出第2代声学響科技技术,提供更优质的开放式骨传导听音体验,透过不一样的音质体验,打造更好的骨传导耳机…...

基于Spring Boot+Thymeleaf的在线投票系统
文章目录 项目介绍主要功能截图:后台登录注册个人信息展示投票数据显示首页展示对战匹配分数排行榜部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅…...

【每日一题Day135】LC1487保证文件名唯一 | 哈希表
保证文件名唯一【LC1487】 给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹:在第 i 分钟,新建名为 names[i] 的文件夹。 由于两个文件 不能 共享相同的文件名,因此如果新建文件夹使用的文件名已经被占用࿰…...
计算机系统的基本组成 第一节
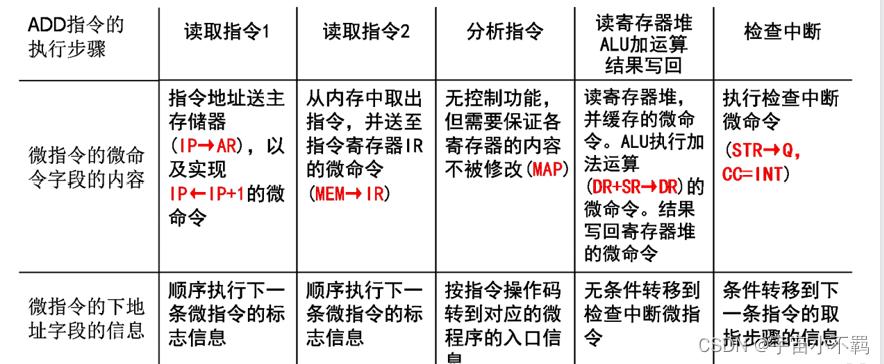
一、计算机系统 计算机系统是指:电子数字通用、计算机系统 由硬件和软件两个子系统组成 硬件是保存和运行软件的物质基础 软件是指挥硬件完成预期功能的智力部分 重点: 计算机系统部件 五个 1、数据运算部件:完成对数据的运算处理功能…...

Scrapy爬虫框架入门
Scrapy是Python开发的一个非常流行的网络爬虫框架,可以用来抓取Web站点并从页面中提取结构化的数据,被广泛的用于数据挖掘、数据监测和自动化测试等领域。下图展示了Scrapy的基本架构,其中包含了主要组件和系统的数据处理流程(图中…...
最新使用nvm控制node版本步骤
一、完全卸载已经安装的node、和环境变量 ①、打开控制面板的应用与功能,搜索node,点击卸载 ②、打开环境变量,将node相关的所有配置清除 ③、打开命令行工具,输入node-v,没有版本号则卸载成功 二、下载nvm安装包 ①…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
