Unity中URP下深度图的线性转化
文章目录
- 前言
- 一、_ZBufferParams参数有两组值
- 二、LinearEyeDepth
- 1、使用
- 2、Unity源码推导:
- 3、使用矩阵推导:
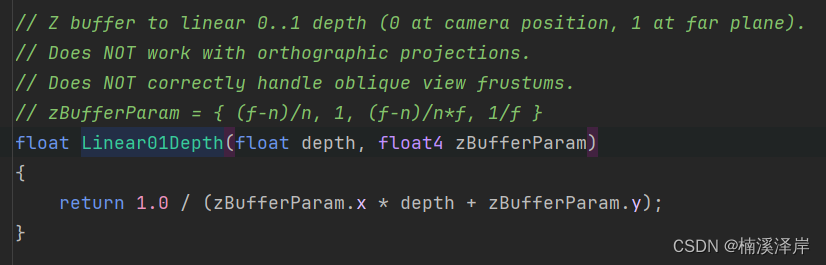
- 三、Linear01Depth
- 1、使用
- 2、Unity源码推导
- 3、数学推导:
前言
在之前的文章中,我们实现了对深度图的使用。因为,深度图不是线性的。所以,在使用时,我们使用了 Linear01Depth 函数对其进行了线性转化。
- Unity中URP下开启和使用深度图
但是,对深度图进行线性转化 还有其他函数。
在这篇文章中,我们来看一下深度图线性转化的 Linear01Depth函数 和 LinearEyeDepth 函数 干了什么。
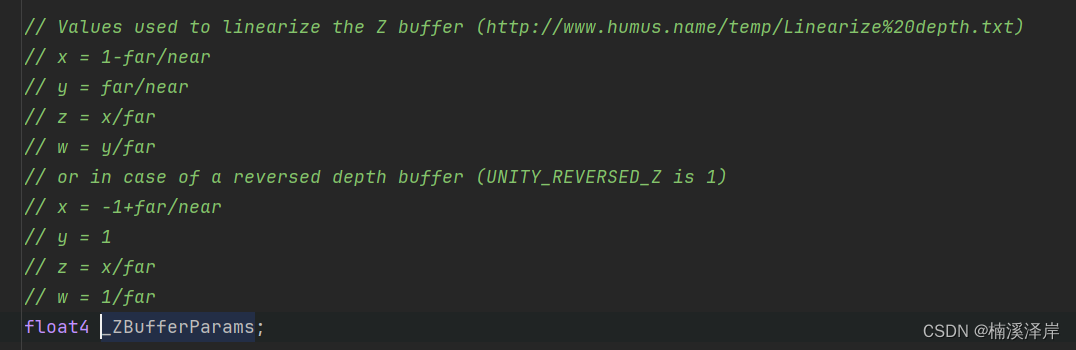
一、_ZBufferParams参数有两组值
-
在OpenGL下

-
在类DirectX下
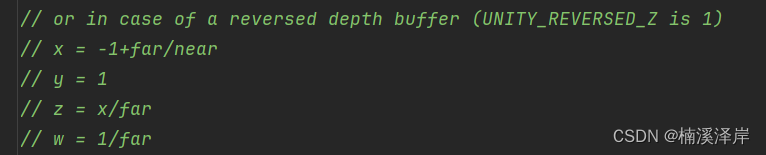
二、LinearEyeDepth
1、使用
-
对采样的深度图纹理进行线性转化
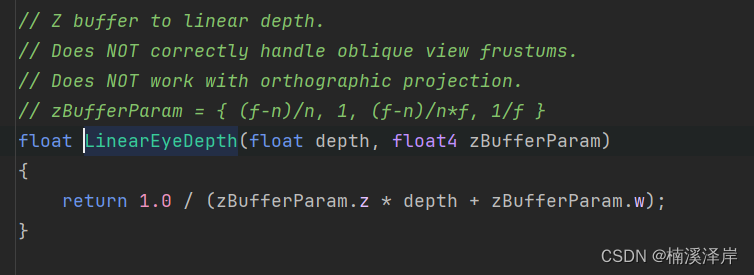
-
转化后的值,就是原来物体的深度 Z 值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = LinearEyeDepth(cameraDepthTex,_ZBufferParams);
- 返回结果全白,效果不明显

- 我们对其取小数部分,使其效果明显一点
frac(depthTex)

2、Unity源码推导:
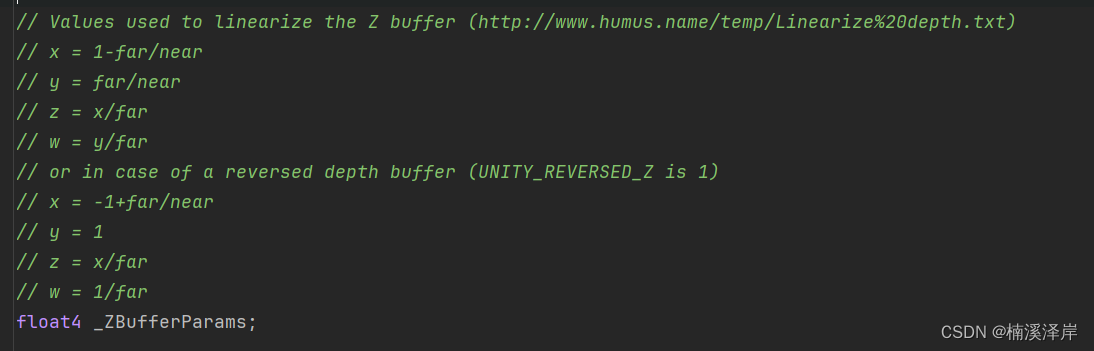
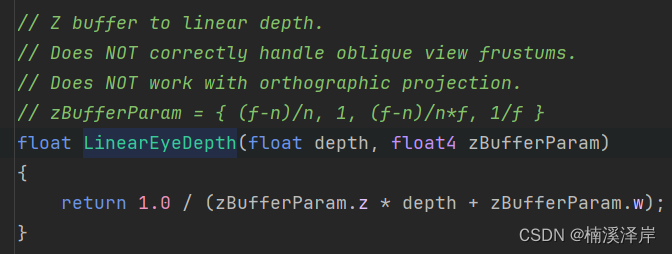
- 这里使用OpenGL下推导
Z v i e w = 1 1 − f n f d + f n f Z_{view}=\frac{1}{\frac{1-\frac{f}{n}}{f}d+\frac{\frac{f}{n}}{f}} Zview=f1−nfd+fnf1
Z v i e w = 1 ( n n − f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n}{n}-\frac{f}{n})\frac{1}{f}d+\frac{1}{n}} Zview=(nn−nf)f1d+n11
Z v i e w = 1 ( n − f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n-f}{n})\frac{1}{f}d+\frac{1}{n}} Zview=(nn−f)f1d+n11
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11
3、使用矩阵推导:
-
OpenGL
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n+f}{n-f} &\frac{2nf}{n-f}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000n−fn+f−100n−f2nf0 -
DirectX
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000f−nn−100f−nnf0 -
由观察空间转化到裁剪空间矩阵可得
Z c l i p = n + f n − f Z v i e w + 2 n f n − f W v i e w Z_{clip}=\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}W_{view} Zclip=n−fn+fZview+n−f2nfWview
W c l i p = − Z v i e w W_{clip}=-Z_{view} Wclip=−Zview -
做透视除法可得
Z n d c = Z c l i p W c l i p = n + f n − f Z v i e w + 2 n f n − f − Z v i e w = n + f f − n + 2 n f ( f − n ) Z v i e w Z_{ndc} = \frac{Z_{clip}}{W_{clip}} = \frac{\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}}{-Z_{view}}=\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}} Zndc=WclipZclip=−Zviewn−fn+fZview+n−f2nf=f−nn+f+(f−n)Zview2nf -
d = 0.5 ⋅ Z n d c + 0.5 d=0.5·Z_{ndc}+0.5 d=0.5⋅Zndc+0.5
d = 0.5 ⋅ ( n + f f − n + 2 n f ( f − n ) Z v i e w ) + 0.5 d = 0.5·(\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}})+0.5 d=0.5⋅(f−nn+f+(f−n)Zview2nf)+0.5 -
我们由 d d d 公式化简,即可得到 Z v i e w Z_{view} Zview
Z v i e w = 1 f − n n f d − 1 n Z_{view} = \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview=nff−nd−n11 -
为了得到正的Z值,需要取反
Z v i e w = − 1 f − n n f d − 1 n Z_{view} =- \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview=−nff−nd−n11
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11
三、Linear01Depth
1、使用
-
对采样的深度图纹理进行线性转化
-
转化后的值,是Z值在[0,1]区间的值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = Linear01Depth(cameraDepthTex,_ZBufferParams);
- 返回结果

2、Unity源码推导
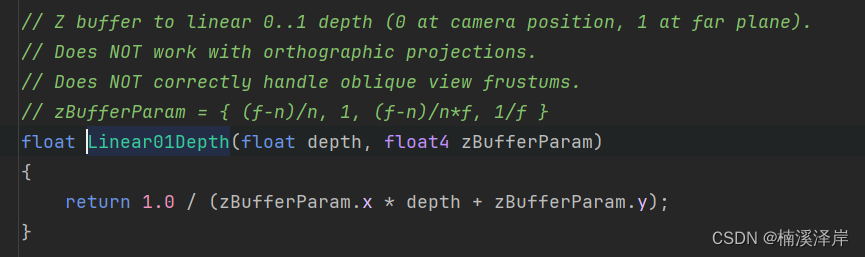
- OpenGL下推导:
Z v i e w = 1 ( 1 − f n ) d + f n Z_{view}= \frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview=(1−nf)d+nf1
3、数学推导:
-
这是LinearEyeDepth下推导出来的
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11 -
Z v i e w Z_{view} Zview的取值范围 [ n e a r , f a r ] [near,far] [near,far]
-
使其除以一个 f f f得到 Linear01Depth函数的结果
Z v i e w = 1 n − f n f d + 1 n ⋅ 1 f = 1 n − f n f d f + f n = 1 ( 1 − f n ) d + f n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}}·\frac{1}{f}=\frac{1}{\frac{n-f}{nf}df+\frac{f}{n}}=\frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview=nfn−fd+n11⋅f1=nfn−fdf+nf1=(1−nf)d+nf1
相关文章:

Unity中URP下深度图的线性转化
文章目录 前言一、_ZBufferParams参数有两组值二、LinearEyeDepth1、使用2、Unity源码推导:3、使用矩阵推导: 三、Linear01Depth1、使用2、Unity源码推导3、数学推导: 前言 在之前的文章中,我们实现了对深度图的使用。因为&#…...

Low Poly Cartoon House Interiors
400个独特的低多边形预制件的集合,可以轻松创建高质量的室内场景。所有模型都已准备好放入场景中,并使用一个纹理创建,以提高性能!包含演示场景! 模型分类: - 墙壁(79件) - 地板(28块) - 浴室(33个) - 厨房(36件) - 厨房道具(68件) - 房间道具(85件) - 灯具(…...
)
[算法与数据结构][c++]:左值、右值、左值引用、右值引用和std::move()
左值、右值、左值引用、右值引用和std::move 1. 什么是左值、右值2. 什么是左值引用、右值引用3. **右值引用和std::move的应用场景**3.1 实现移动语义3.2 **实例:vector::push_back使用std::move提高性能** **4. 完美转发 std::forward**5. Reference 写在前面&…...

【QT】day3
1.登陆界面 2.登陆失败 3.登陆成功弹窗 4.点击OK后跳转 #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow) {ui->setupUi(this); }MainWindow::~MainWindow…...

c++ fork, execl 参数 logcat | grep
Linux进程编程(PS: exec族函数、system、popen函数)_linux popen函数会新建进程吗-CSDN博客 execvp函数详解_如何在C / C 中使用execvp()函数-CSDN博客 C语言的多进程fork()、函数exec*()、system()与popen()函数_c语言 多进程-CSDN博客 Linux---fork…...
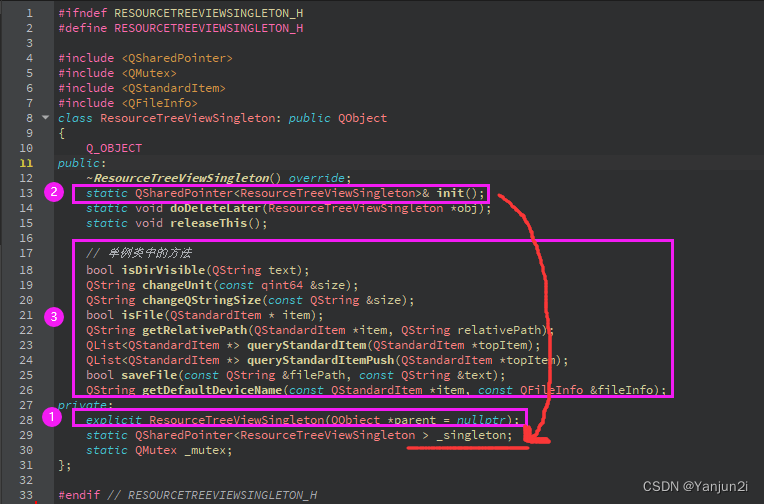
QT:单例
单例的定义 官方定义:单例是指确保一个类在任何情况下都绝对只有一个实例,并提供一个全局访问点。 单例的写法 抓住3点: 构造函数私有化(确保只有一个实例)提供一个可以获取构造实例的接口(提供唯一的实…...

IPv6路由协议---IPv6动态路由(OSPFv3-4)
OSPFv3的链路状态通告LSA类型 链路状态通告是OSPFv3进行路由计算的关键依据,链路状态通告包含链路状态类型、链路状态ID、通告路由器三元组唯一地标识了一个LSA。 OSPFv3的LSA头仍然保持20字节,但是内容变化了。在LSA头中,OSPFv2的LS age、Advertising Router、LS Sequence…...
移动通信原理与关键技术学习(4)
1.小尺度衰落 Small-Scale Fading 由于收到的信号是由通过不同的多径到达的信号的总和,接收信号的增强有一定的减小。 小尺度衰落的特点: 信号强度在很小的传播距离或时间间隔内的快速变化;不同多径信号多普勒频移引起的随机调频ÿ…...

第二百五十八回
文章目录 1. 概念介绍2. 思路与方法2.1 实现思路2.2 实现方法 3. 示例代码4. 内容总结 我们在上一章回中介绍了"模拟对话窗口的页面"相关的内容,本章回中将介绍如何创建一个可以输入内容的对话框.闲话休提,让我们一起Talk Flutter吧。 1. 概念…...

freesurfer-reconall后批量提取TIV(颅内总体积)
#提取TIV #singleline=$(grep Estimated Total Intracranial Volume /usr/local/freesurfer/subjects/bect-3d+bold-wangjingchen-4.9y-2/stats/aseg.sta...

【GO】如何用 Golang 的 os/exec 执行 pipe 替换文件
背景 主要记录一下怎么用 Golang 的 os/exec 去执行一个 cmd 的 pipeline,就是拿 cmdA 的输出作为 cmdB 的输入,这里记录了两种方法去替换文件里面的字符串。 pipe 那个逻辑在 demo1 里。 另外一种是直接读文件做替换,一不小心两个都放进来了…...
基于Spring-boot-websocket的聊天应用开发总结
目录 1.概述 1.1 Websocket 1.2 STOMP 1.3 源码 2.Springboot集成WS 2.1 添加依赖 2.2 ws配置 2.2.1 WebSocketMessageBrokerConfigurer 2.2.2 ChatController 2.2.3 ChatInRoomController 2.2.4 ChatToUserController 2.3 前端聊天配置 2.3.1 index.html和main.j…...

2023年度总结 - 职业生涯第一个十年
2023年只剩下最后一周,又到了一年一度该做年末总结的时候了。 回想起去年,还有人专门建立了一个关于年度总结文章汇总的仓库。读了很多篇别人写的,给了我很多的触动和感想。这里的每篇文章都是关于某个人这一整年的生活和工作的轨迹啊。即使你…...
setup 语法糖
只有vue3.2以上版本可以使用 优点: 更少的样板内容,更简洁的代码 能够使用纯 Typescript 声明props 和抛出事件 更好的运行时性能 更好的IDE类型推断性能 在sciprt标识上加上setup 顶层绑定都可以使用 不需要return ,可以直接使用 使用组件…...
Javaweb之Mybatis的基础操作的详细解析
1. Mybatis基础操作 学习完mybatis入门后,我们继续学习mybatis基础操作。 1.1 需求 需求说明 通过分析以上的页面原型和需求,我们确定了功能列表: 查询 根据主键ID查询 条件查询 新增 更新 删除 根据主键ID删除 根据主键ID批量删除 …...

知名开发者社区Stack Overflow发布《2023 年开发者调查报告》
Stack Overflow成立于2008年,最知名的是它的公共问答平台,每月有超过 1 亿人访问该平台来提问、学习和分享技术知识。是世界上最受欢迎的开发者社区之一。每年都会发布一份关于开发者的调查报告,来了解不断变化的开发人员现状、正在兴起或衰落…...

vue element plus Form 表单
表单包含 输入框, 单选框, 下拉选择, 多选框 等用户输入的组件。 使用表单,您可以收集、验证和提交数据。 TIP Form 组件已经从 2. x 的 Float 布局升级为 Flex 布局。 典型表单# 最基础的表单包括各种输入表单项,比如input、select、radio、checkbo…...

zmq_connect和zmq_poll
文章内容: 介绍函数zmq_connect和zmq_poll的使用 zmq_connect zmq_connect函数是ZeroMQ库中的一个函数,用于在C语言中创建一个与指定地址的ZeroMQ套接字的连接。该函数的原型如下: int zmq_connect(void *socket, const char *endpoint);其…...
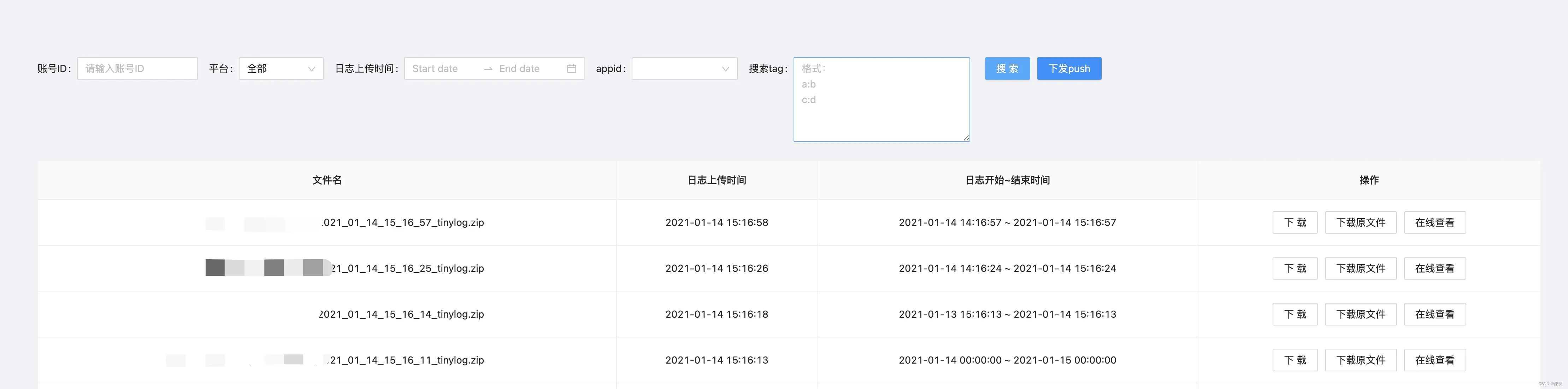
TinyLog iOS v3.0接入文档
1.背景 为在线教育部提供高效、安全、易用的日志组件。 2.功能介绍 2.1 日志格式化 目前输出的日志格式如下: 日志级别/[YYYY-MM-DD HH:MM:SS MS] TinyLog-Tag: |线程| 代码文件名:行数|函数名|日志输出内容触发flush到文件的时机: 每15分钟定时触发…...

react-native 配置@符号绝对路径配置和绝对路径没有提示的问题
这里需要用到vscode的包 yarn add babel-plugin-module-resolver 找到根目录里的babel.config.js 在页面添加plugins配置 直接替换 module.exports {presets: [module:metro-react-native-babel-preset],plugins: [[module-resolver,{root: [./src],alias: {/utils: ./src/…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
