存在重复元素模块-三道题
文章目录
- 存在重复元素
- 217. 存在重复元素
- 219. 存在重复元素 II
- 220. 存在重复元素 III (SortedList+二分)
- 小结
存在重复元素
217. 存在重复元素
题目链接:217. 存在重复元素
题目大意:给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
注意:(1)1 <= nums.length <= 10510^5105;(2)−109-10^9−109 <= nums[i] <= 10910^9109。
示例:
输入:nums = [1,2,3,1]
输出:true输入:nums = [1,2,3,4]
输出:false输入:nums = [1,1,1,3,3,4,3,2,4,2]
输出:true
参考代码:
class Solution:def containsDuplicate(self, nums: List[int]) -> bool:# 取巧return len(set(nums)) != len(nums)'''# hash maphash_map = dict()for num in nums:if num not in hash_map:hash_map[num] = 1else:return Truereturn False''''''# 计数器counter = collections.Counter(nums)for num in nums:if counter[num] > 1:return Truereturn False'''
- (1)取巧办法:
- 时间复杂度:O(1)O(1)O(1)。
- 空间复杂度:O(n)O(n)O(n),其中 nnn 是 numsnumsnums 的长度。
- (2)hash map办法:
- 时间复杂度:O(n)O(n)O(n)
- 空间复杂度:O(n)O(n)O(n)
- (3)计数器办法:
- 时间复杂度:O(n)O(n)O(n)
- 空间复杂度:O(n)O(n)O(n)
219. 存在重复元素 II
题目链接:219. 存在重复元素 II
题目大意:给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在,返回 true ;否则,返回 false 。
注意:(1)1 <= nums.length <= 10510^5105;(2)−109-10^9−109 <= nums[i] <= 10910^9109;(3)0 <= k <= 10510^5105。
示例:
输入:nums = [1,2,3,1], k = 3
输出:true输入:nums = [1,0,1,1], k = 1
输出:true输入:nums = [1,2,3,1,2,3], k = 2
输出:false
参考代码:
class Solution:def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:hash_map = dict()for i,num in enumerate(nums):if num not in hash_map:hash_map[num] = ielse:if i - hash_map[num] <= k:return Truehash_map[num] = ireturn False
- 时间复杂度:O(n)O(n)O(n),其中 nnn 是 numsnumsnums 的长度。
- 空间复杂度:O(n)O(n)O(n)
220. 存在重复元素 III (SortedList+二分)
题目链接:220. 存在重复元素 III
题目大意:给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j,使得 abs(nums[i] - nums[j]) <= t ,同时又满足 abs(i - j) <= k 。
如果存在则返回 true,不存在返回 false。
注意:(1)0 <= nums.length <= 2∗1042 * 10^42∗104;(2)−231-2^{31}−231 <= nums[i] <= 231−12^{31} - 1231−1;(3)0 <= k <= 10410^4104;(4)0 <= t <= 231−12^{31} - 1231−1。
示例:
输入:nums = [1,2,3,1], k = 3, t = 0
输出:true输入:nums = [1,0,1,1], k = 1, t = 2
输出:true输入:nums = [1,5,9,1,5,9], k = 2, t = 3
输出:false
参考代码:
from sortedcontainers import SortedList class Solution:def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:wd = SortedList()n = len(nums)for i in range(n):# print(wd)if i>k:wd.remove(nums[i-1-k])wd.add(nums[i])idx = bisect.bisect_left(wd,nums[i])if idx>0 and abs(wd[idx]-wd[idx-1])<=t:return Trueif idx<len(wd)-1 and abs(wd[idx+1]-wd[idx])<=t:return Truereturn False
- 时间复杂度:O(nlogk)O(n \log{k})O(nlogk),其中 nnn为数组的长度,TreeSet 基于红黑树,查找和插入都是 O(logk)O(\log{k})O(logk) 复杂度。
- 空间复杂度:O(k)O(k)O(k)
小结
- 这三道题挺有趣的,之间的关联并不是非常大,不过都用到了哈希表这个容器,是一套不错的练习题,总结记录一下,便于快速查询,加油(23.3.3)。
相关文章:

存在重复元素模块-三道题
文章目录存在重复元素217. 存在重复元素219. 存在重复元素 II220. 存在重复元素 III (SortedList二分)小结存在重复元素 217. 存在重复元素 题目链接:217. 存在重复元素 题目大意:给你一个整数数组 nums 。如果任一值在数组中出…...

3种方法删除7-Zip压缩包的密码
7-Zip压缩软件是一款完全免费且开源的软件,不仅能压缩和解压7-Zip压缩包,还能给压缩包设置打开密码。 有些小伙伴可能会遇到这样的问题,7-Zip压缩包设置密码后,过了一段时间不需要密码保护了,或者一不小心忘记了密码&…...

Codeforces Round 855 (Div. 3)(A~F)
A. Is It a Cat?定义满足条件的字符串为:其中仅可能含有meow四种字母的大小写,而且相同种类的字母必须挨在一起,四种字母的顺序必须按照meow排列。给出一个字母串,求是否满足条件。思路:感觉是个很麻烦的模拟。首先把…...
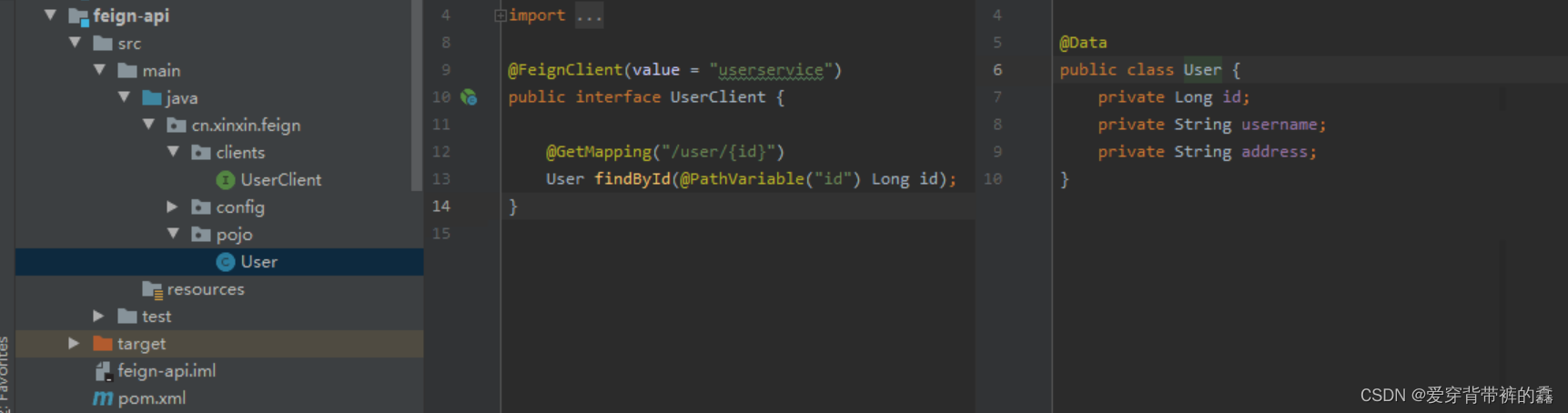
【SpringCloud】SpringCloud详解之Feign实战
目录前言SpringCloud Feign远程服务调用一.需求二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用(order服务内编写)四.使用Feign远程调用(order服务内配置)五.自定义Feign配置(order服务内配置)六.Feign配置日志(oder服务内配置)七.Feign调优(order服务内配置)八.抽…...

tuts4you上lena‘s40个crackme(1)
本来是不打算写文章了,因为懒,想以后通过录屏的形式保存一下自己学的路程。但奈何开学后一直没找到机会,在宿舍也不愿意大吼大叫的讲东西,只好再写写文章了 最近学了一些汇编语言和逆向工程,所以就想通过这40给题目来看…...

研讨会回顾 | Perforce版本控制工具Helix Core入华十年,携手龙智赋能企业大规模研发
2023年2月28日,龙智联合全球领先的数字资产管理工具厂商Perforce共同举办Perforce on Tour网络研讨会,主题为“赋能‘大’研发,助力‘快’交付”。 作为Perforce Helix Core产品在中国地区的唯一授权合作伙伴,龙智董事长何明女士为…...

C++ vscode 开发环境搭建
C vscode 开发环境搭建 笔记内容: C vscode 开发环境搭建准备了解g命令编译调试掌握使用launch.json和tasks.json配置文件编译调试了解使用cmake构建 git: https://github.com/weichangk/hellocpp/tree/master/vscodecmakecpp 环境搭建准备 安装vscode安装qt&a…...

ANR系列(二)——ANR监听方案之SyncBarrier
前言 在项目中经常遇到了手机假死问题,无规律的偶现问题,大量频繁随机操作后,便会出现假死,整个应用无法操作,不会响应事件,会发生各种奇怪的ANR,且trace不固定。而SyncBarrier是其中的罪魁祸首…...

【完美解决】应用程序无法正常启动(0xc000007b)请单击“确定”关闭应用程序
年期安装CorelDRAW X8 (64-Bit),安装完成之后运行一点毛病都没有,可是过了两三个月,再打开就出现“应用程序无法正常启动(0xc000007b)请单击“确定”关闭应用程序”这个提示框,如下图示 出现这个问题我就上网查找,无非…...

.NET基础加强第二课--静态成员,静态类
类 实例类 默认是实例类 静态类 在类前加上static ,就是静态类 静态类中,所有包含的成员必须是静态成员 实例成员是属于具体某个对象的 举例代码 Person p1 new Person(); p1.Age 20; p1.Name “张三”; class Person { public string Name { get; set;…...

【UML+OOPC嵌入式C语言开发】使用C语言实现一个面向对象语言才能够实现的类
文章目录简述OOPC开发环境知识讲解函数示例类的实现示例接口实现示例(前面两部分有点无聊,如果大家没兴趣看可以直接从知识讲解开始看) 简述OOPC oopc,是一种轻量级的面向对象的C语言编程框架, LW_OOPC是Light-Weight …...
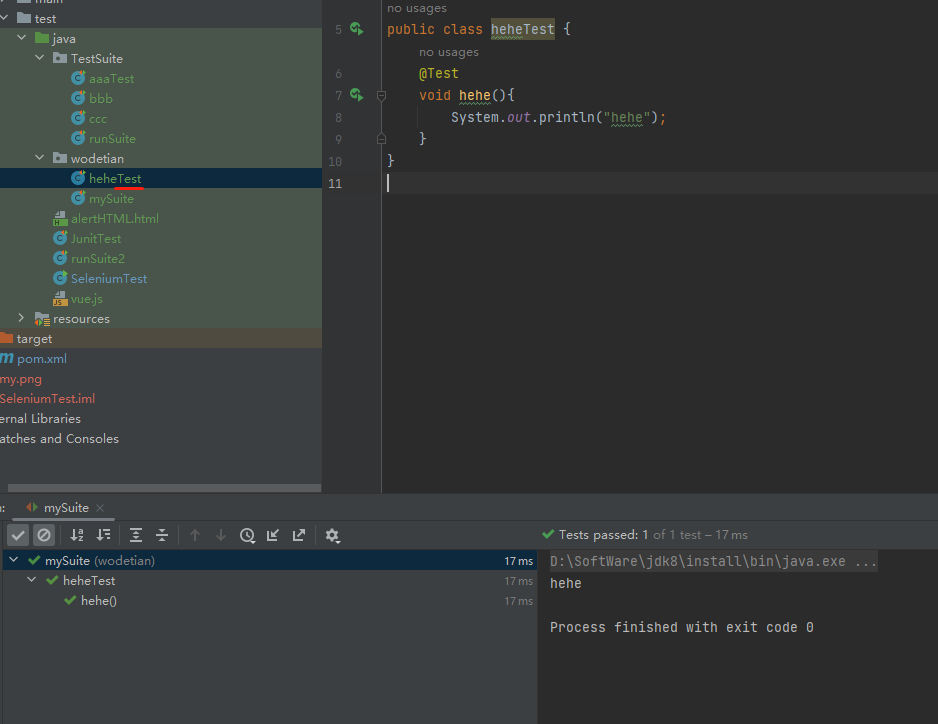
软件测试自动化Java篇【Selenium+Junit 5】
文章目录Selenium环境部署自动化测试例子常见的元素操作窗口等待浏览器的操作弹窗选择器执行脚本文件上传浏览器参数Junit 5导入依赖Junit 4 和 Junit5 注解对比断言测试顺序参数化单参数多参数动态参数测试套件指定类来运行测试用例指定包名来运行包下测试用例Selenium 为什么…...
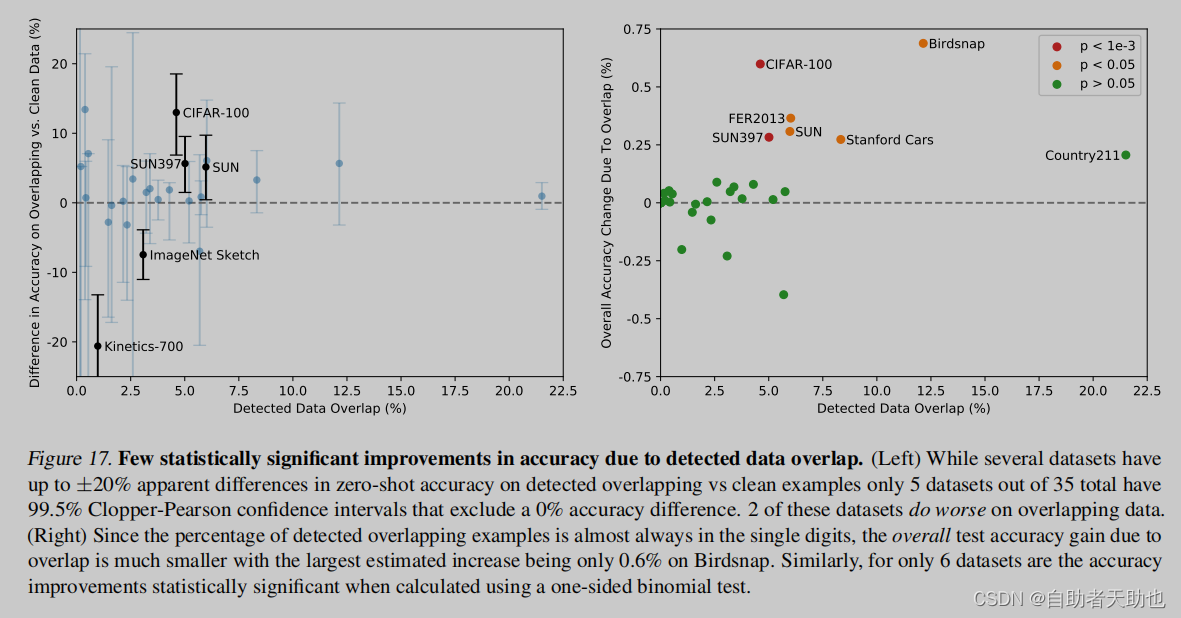
Clip:学习笔记
Clip 文章目录Clip前言一、原理1.1 摘要1.2 引言1.3 方法1.4 实验1.4.1 zero-shot Transfer1.4.2 PROMPT ENGINEERING AND ENSEMBLING1.5 局限性二、总结前言 阅读论文: Learning Transferable Visual Models From Natural Language Supervision CLIP 论文逐段精读…...
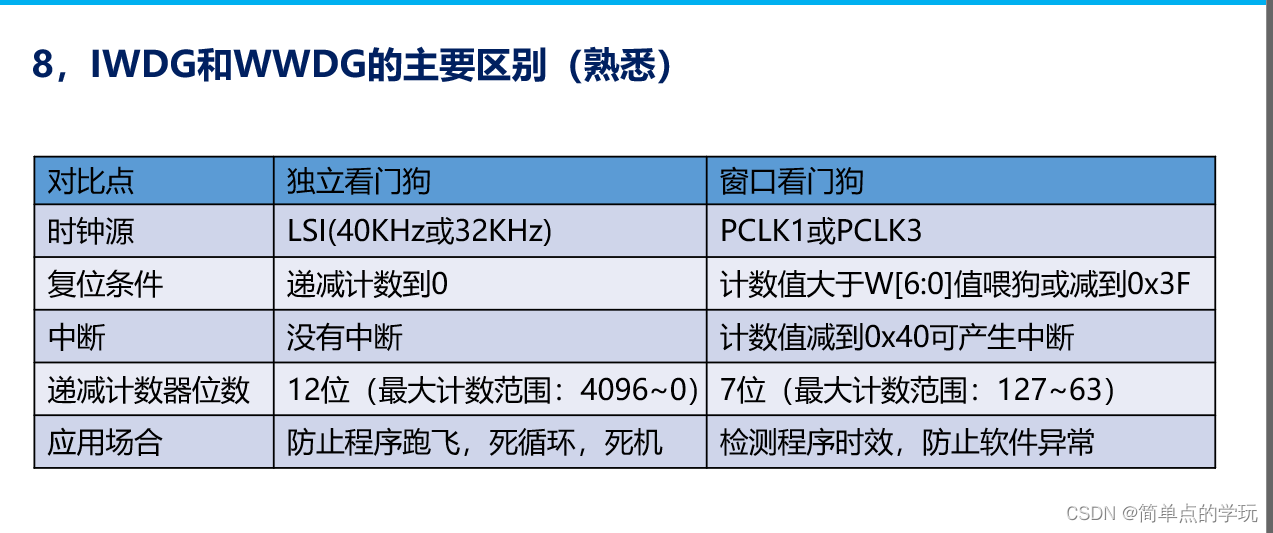
STM32CubexMX与FreeRTOS学习
目录 LED与EXTI配置 基本定时器使用 软件定时器 在HAL库中实现printf 重点--记得自己添加头文件 队列实现 二值信号量实现 计数信号量实现 DMA实现 ADC配置 RTC配置 看门狗 窗口看门狗 FreeRTOS结合MX软件开发,基础配置直接生成,我们只…...

Master Slave 主从同步错误 Slave_IO_Running:NO/Slave_SQL_Running: No
Master Slave 主从同步错误 Slave_IO_Running:NO Slave_SQL_Running:Yes #在Slave库上查看状态 mysql> show slave status\G Slave_IO_Running: No Slave_SQL_Running: Yes #重启master库:service mysqld restart mysql> show master status; ------------…...
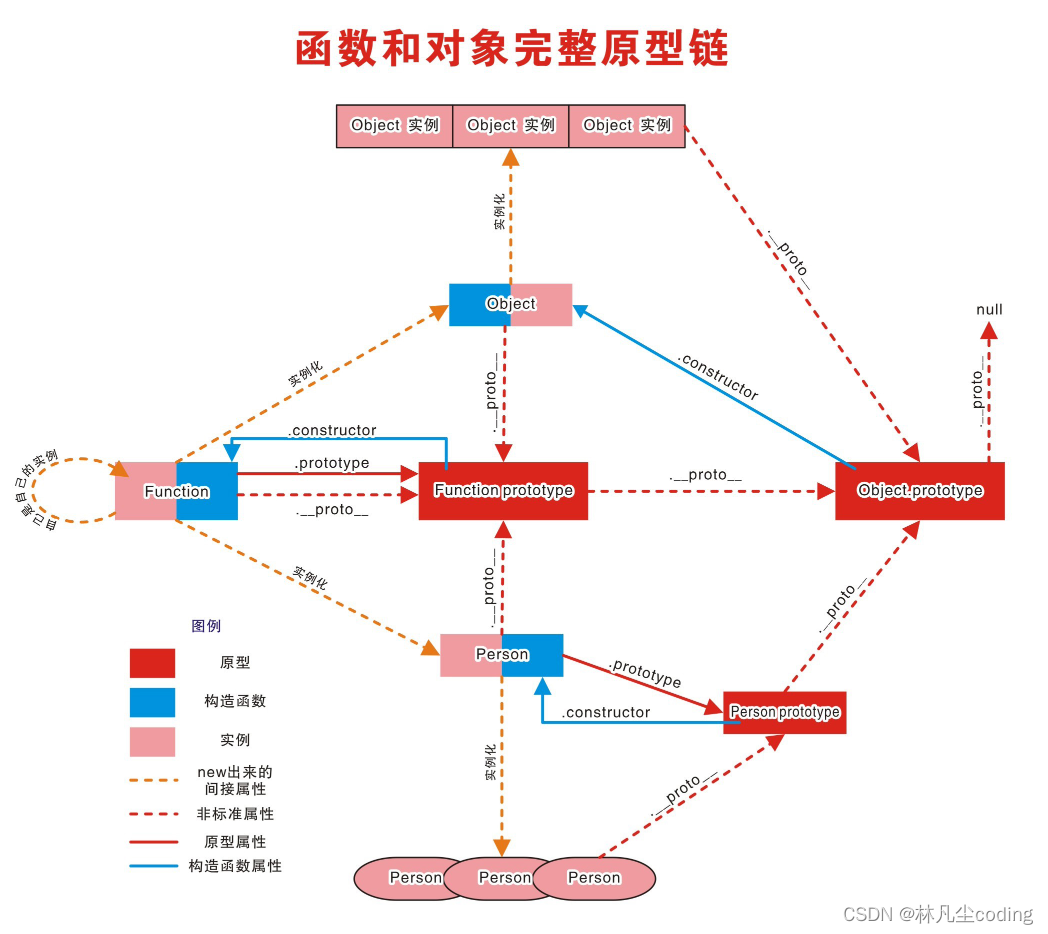
JavaScript函数之prototype原型和原型链
文章目录1. 原型2. 显式和隐式原型3. 原型链3.1 访问顺序4. instanceof4.1 如何判断1. 原型 函数的prototype属性 每个函数都有一个prototype属性,它默认指向一个Object空对象(即:原型对象)。原型对象中有一个属性constructor&a…...
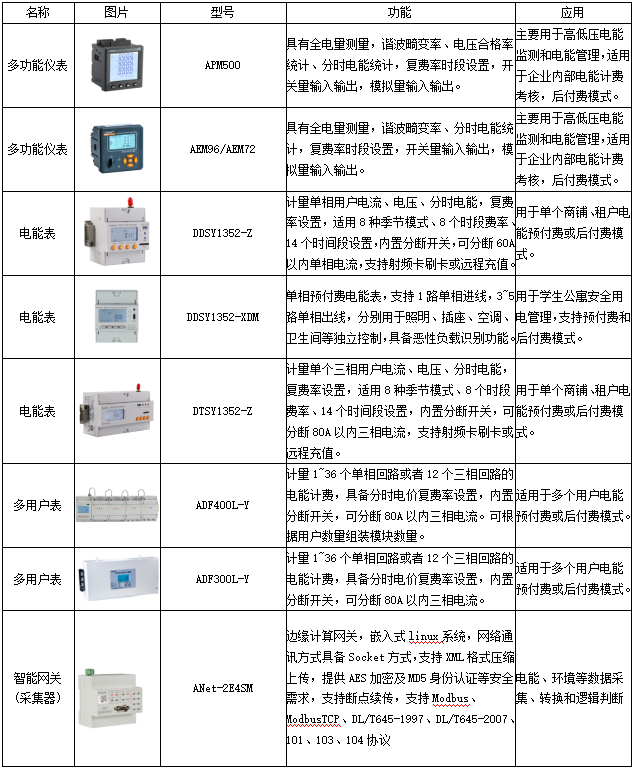
从上海分时电价机制调整看转供电用户电能计费
安科瑞 耿敏花2022年12月16日,上海市发改委发布《关于进一步完善我市分时电价机制有关事项的通知》(沪发改价管〔2022〕50号)。通知明确上海分时电价机制,一般工商业及其他两部制、大工业两部制用电夏季(7、8、9月)和冬季…...

TypeScript类型体操:获取数组中元素对象属性的值作为新类型
title: TypeScript类型体操:获取数组中元素对象属性的值作为新类型 date: 2023-03-03 20:58:24 categories: TypeScript类型体操 tags: TypeScript类型体操TypeScript 首先先说获取数组中元素对象属性的值作为新类型的解决方案 使用 as const 强调不可变数组使用 …...

npm,yarn和pnpm
npm扁平的node_modules结构比如项目依赖了A 和 C,而 A 和 C 依赖了不同版本的 B1.0 和 B2.0,D也依赖B1.0, node_modules 结构如下:node_modules ├── A1.0.0 ├── B1.0.0 └── C1.0.0└── node_modules└── B2.0.0C依赖的B2.0因为版…...
)
【算法】【数组与矩阵模块】在排好序的矩阵中找数,时间复杂度O(M+N)
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
