【C++进阶05】AVL树的介绍及模拟实现

一、AVL树的概念
二叉搜索树的缺点
二叉搜索树虽可以缩短查找效率
但如果数据有序或接近有序
二叉搜索树将退化为单支树
查找元素相当于在顺序表中搜索元素,效率低下
AVL树便是解决此问题
向二叉搜索树中插入新结点
并保证每个结点的左右子树
高度之差的绝对值不超过1
(需要对树中的结点进行调整)
即可降低树的高度,从而减少
平均搜索长度
AVL树或空树
或是具有以下性质的二叉搜索树
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)
的绝对值不超过1(-1/0/1)
AVL树不一定有平衡因子
平衡因子只是其中一种实现方式
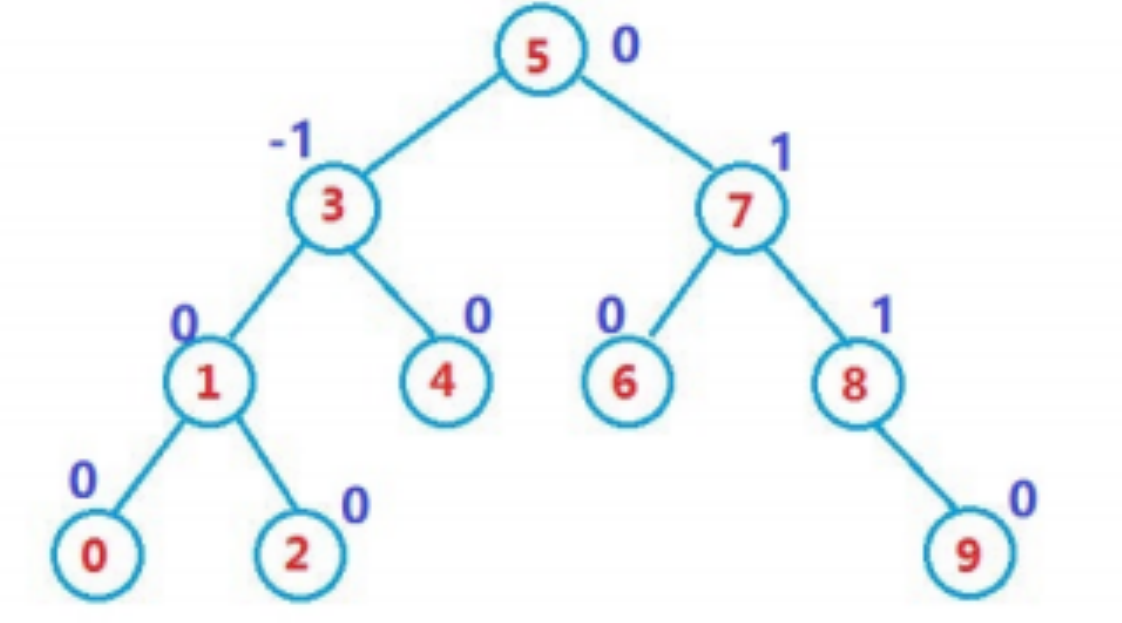
如果一棵二叉搜索树是高度平衡的
它就是AVL树,如果它有n个结点
其高度可保持在 O ( l o g 2 n ) O(log_2 n) O(log2n)
搜索时间复杂度O( l o g 2 n log_2 n log2n)
二、AVL树实现的基本框架
2.1 AVL树节点的定义
template <class K, class V>
struct AVLTreeNode
{// 三叉链AVLTreeNode<K, V>* _left; AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//存储的键值对 pair<K, V> _KV;// balance factor 平衡因子int _bf; // 构造函数AVLTreeNode(const pair<K, V>& kv), left(nullptr), right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};
2.2 AVL树的基本结构
template <class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
private:Node* _root = nullptr; // 根节点
};
2.3 AVL树的插入
AVL树插入步骤:
按二叉搜索树的方式插入新节点更新平衡因子若平衡因子失衡,需要旋转处理
平衡因子失衡后的旋转处理
-
更新完, 平衡因子没问题(|bf| <= 1)
平衡因子结构未受影响, 不需要处理 -
更新完,平衡因子有问题(|bf| > 1)
平衡结构受影响,需要处理(旋转)
原因:
插入新增节点
会影响祖先的平衡因子(全部或部分)
当前节点平衡因子等于
右树节点个数减左树节点个数
- cur == parent->right 则parent->bf++
- cur == parent->left 则parent->bf–
parent所在子树高度发生变化
则需要继续往上更新爷爷节点
否则就不更新
parent->bf == 1 || parent->bf == -1
// 则说明parent所在子树变了, 继续更新
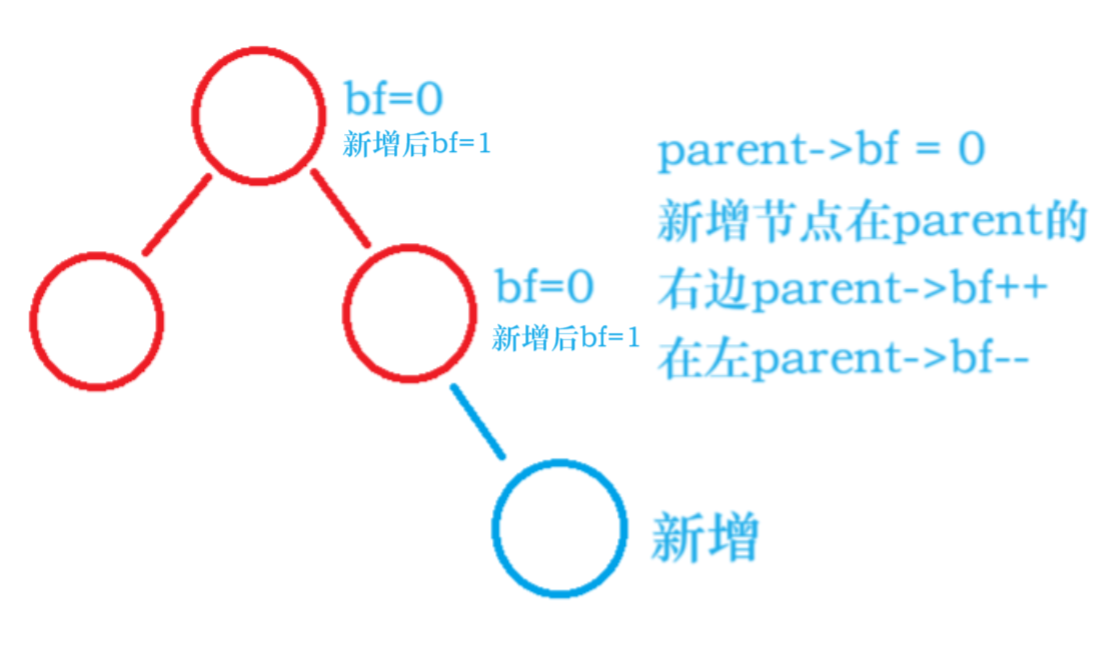
插入节点更新平衡因子后分为三种情况
- 插入前parent->bf == 0
说明插入前左右两边高度相等
插入后有一边高1
说明parent一边高,一边低,高度变了
2.
parent->bf == 2 || parent->bf == -2
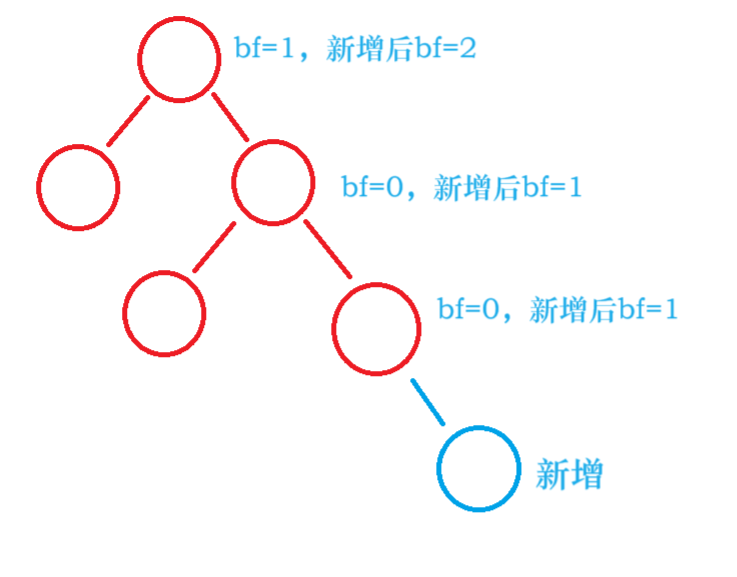
则说明parent所在子树不平衡
需要处理这颗子树(旋转处理)
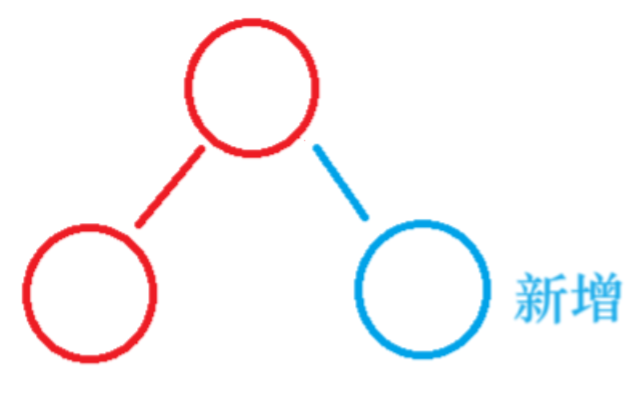
- parent->bf == 0
parent所在子树高度不变
不用继续往上更新,这一次插入结束
说明插入前parent->bf == 1 or -1
插入前一边高,一边低
插入节点填上矮的那边,高度不变
三、AVL树的旋转
旋转的原则:
保持它是搜索树
旋转的目的:
- 让这棵子树平衡
- 降低这棵子树的高度
左旋过程
- 30的左子树
25变成20的右子树 20变成30的左子树
30变成整棵树的根
实际旋转中的节点值可能不是这些值
但也是按这些点位去旋转的
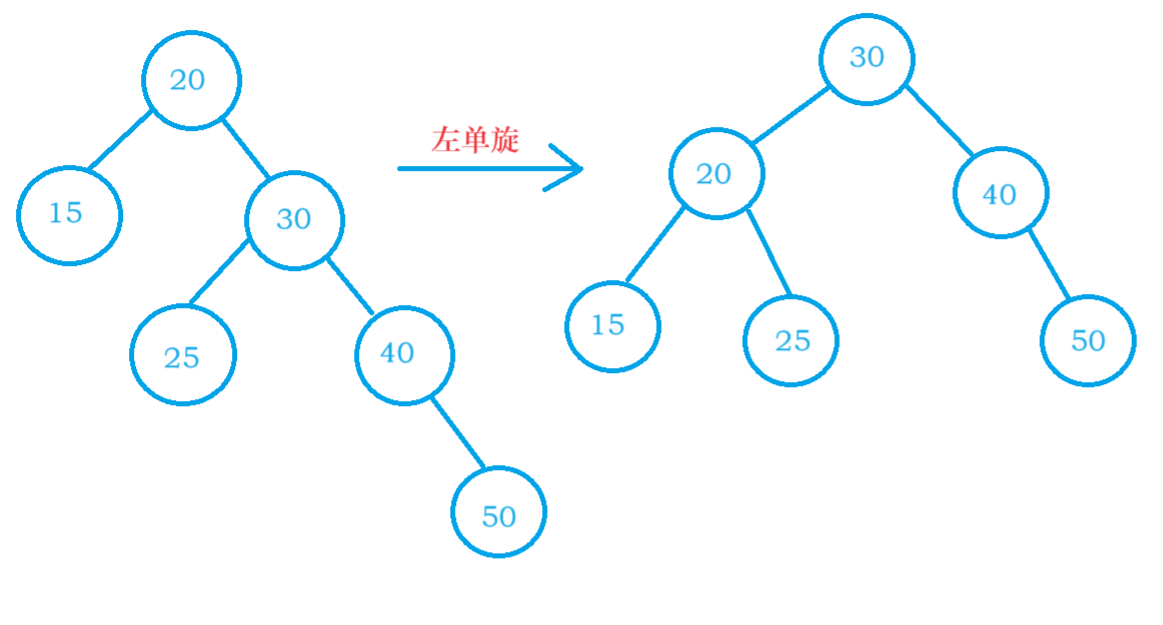
根据节点插入位置的不同
AVL树的旋转分为四种:
1. 新节点插入较高左子树的左侧—左左:
右单旋
图中h为子树的高度
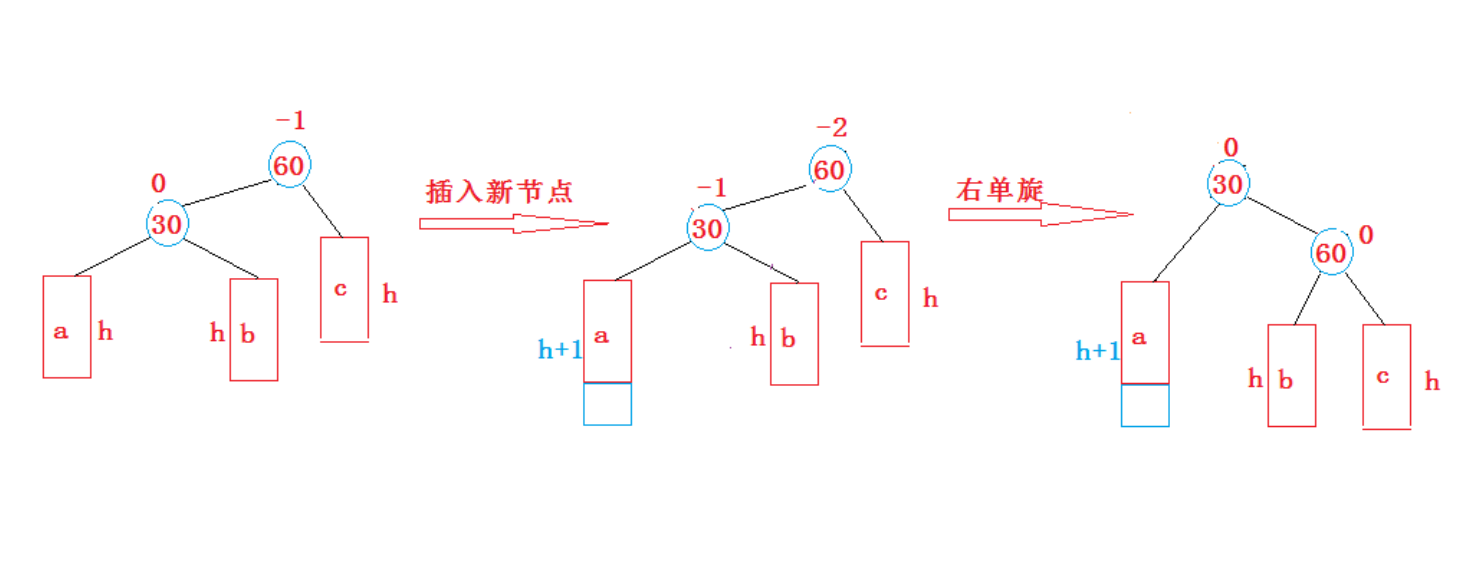
2. 新节点插入较高右子树的右侧—右右:
左单旋
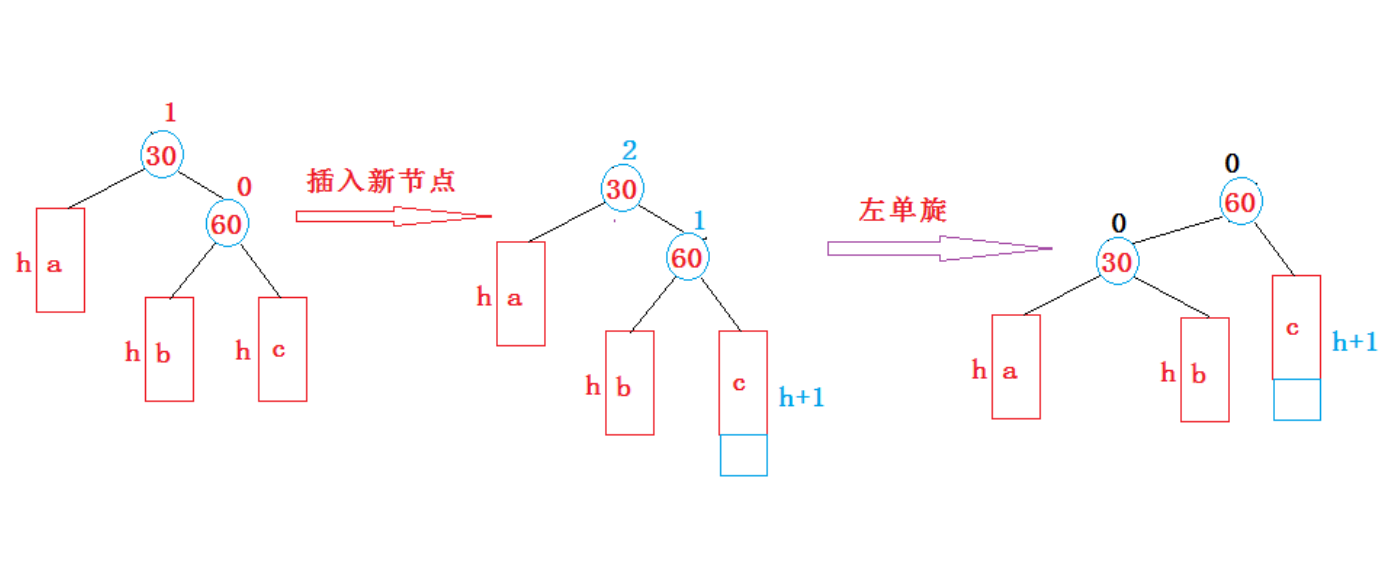
3. 新节点插入较高左子树的右侧—左右:
先左单旋再右单旋
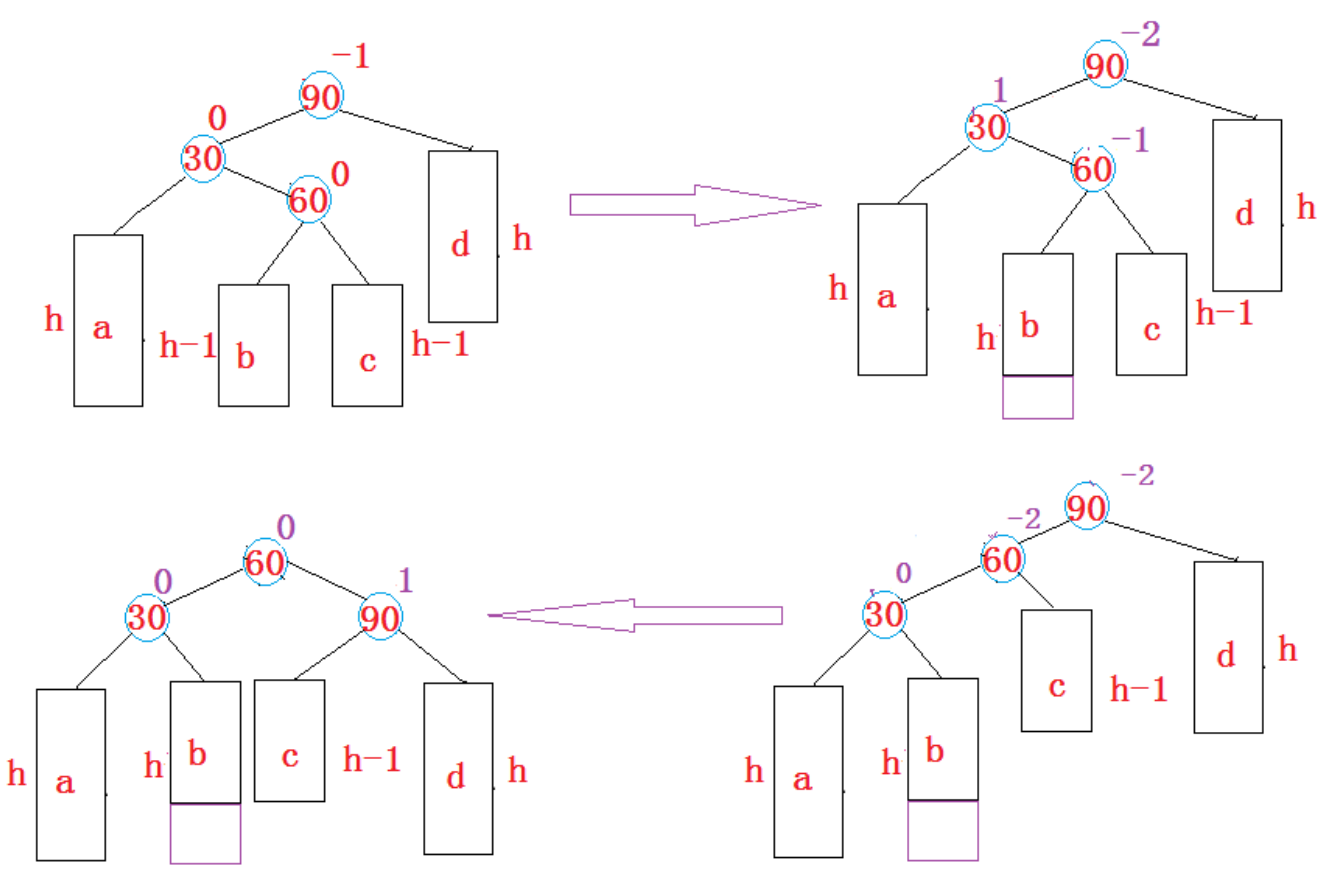
将双旋变成单旋后再旋转,即:
先对30进行左单旋
然后再对90进行右单旋
图中只展示了b插入引发双旋的场景
本质有三种引发双旋的场景:
- 在b插入,b的高度变化+1
- 在c插入,c的高度变化+1
- 60本身就是新增节点
旋转完成后再考虑平衡因子的更新
不同场景的插入,60的平衡因子也不同
分别为-1,1,0
且每种场景的插入旋转完后90和30的
平衡因子都不一样
代码的实现通过记录60这个点位的平衡因子
旋转完后
根据不同场景的插入更新90和30的平衡因子
4. 新节点插入较高右子树的左侧—右左:
先右单旋再左单旋
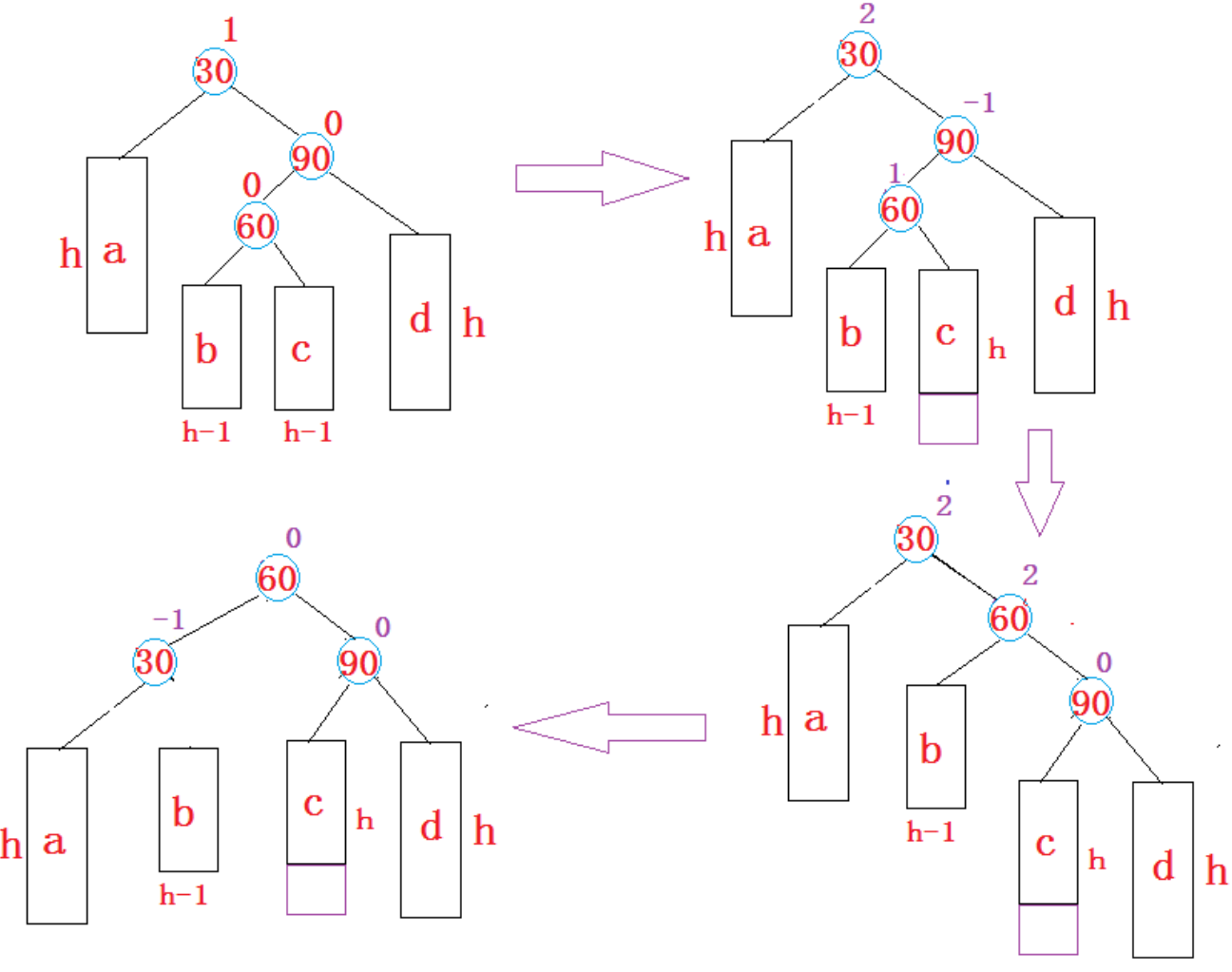
参考先左单旋再右单旋
四、插入代码的实现
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first) // 插入节点比当前节点大往右走, 小往左走{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 链接cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}// new的节点的parent还指向空cur->_parent = parent;// 1. 更新平衡因子while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 1 || parent->_bf == -1){// 继续更新parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == 0){break;}else if (parent->_bf == 2 || parent->_bf == -2){// 需要旋转处理 --- 1. 让这棵子树平衡 2. 降低这棵子树的高度if (parent->_bf == 2 && cur->_bf == 1) // parent->right是cur{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1) // parent->{RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break; // 处理完,break,否则会一直循环}else{// 如果插入之前就有问题assert(false);}}return true;
}
五、AVL树旋转代码实现
void RotateL(Node* parent) // 左单旋
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) // subRL可能为空subRL->_parent = parent;// 旋转的不一定是整棵树Node* pparent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (pparent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}parent->_bf = subR->_bf = 0;
}void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* pparent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr){_root = subL;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}parent->_bf = subL->_bf = 0;
}void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);subLR->_bf = 0; // subLR的左一定等于0if (bf == 1){parent->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subL->_bf = 0;}else{assert(false);}
}void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);subRL->_bf = 0;if (bf == 1){parent->_bf = -1;subR->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;}else if (bf == 0){parent->_bf = 0;subR->_bf = 0;}else{assert(false);}
}
六、全部代码实现
AVL树模拟实现全部代码:gitee链接
相关文章:

【C++进阶05】AVL树的介绍及模拟实现
一、AVL树的概念 二叉搜索树的缺点 二叉搜索树虽可以缩短查找效率 但如果数据有序或接近有序 二叉搜索树将退化为单支树 查找元素相当于在顺序表中搜索元素,效率低下 AVL树便是解决此问题 向二叉搜索树中插入新结点 并保证每个结点的左右子树 高度之差的绝对值不超…...
MySQL视图 索引 面试题
一. 视图 视图:一种虚拟存在的表,行和列的数据来自定义视图的查询中使用的表,并且是在使用视图时动态生成的,只保存了sql逻辑,不保存查询结果 视图语法 -- 创建 create view 视图名 as 查询语句;-- 使用 select * f…...
JAVA实现文件上传至阿里云
注册阿里云账号后,开通好对象存储服务(OSS),三个月试用 阿里云登录页 (aliyun.com) 目录 一.创建Bucket 二.获取AccessKey(密钥) 三.参考官方SDK文件,编写入门程序 1.复制阿里云OSS依赖,粘贴…...
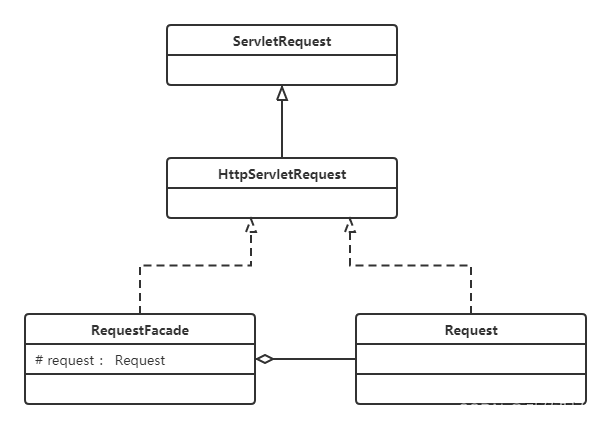
设计模式之外观模式【结构型模式】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档> 学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某…...

Qt QCheckBox复选按钮控件
文章目录 1 属性和方法1.1 文本1.2 三态1.3 自动排他1.4 信号和槽 2 实例2.1 布局2.2 代码实现 Qt中的复选按钮类是QCheckBox它和单选按钮很相似,单选按钮常用在“多选一”的场景,而复选按钮常用在"多选多"的场景比如喜欢的水果选项中…...

加速科技ST2500 数模混合信号测试设备累计装机量突破500台!
国产数字机,测试中国芯!新年伊始,国产半导体测试设备领军企业加速科技迎来了振奋人心的一刻,ST2500 数模混合信号测试设备累计装机量突破500台!加速科技凭借其持续的创新能力、完善的解决方案能力、专业热忱的本地化服…...
ASP.NETCore WebAPI 入门 杨中科
ASP.NETCore WebAPI入门1 回顾 mvc开发模式 前端代码和后端代码是混在一个项目之中 WEB API 1、什么是结构化的Http接口。Json。 2、Web API项目的搭建。 3、Web API项目没有Views文件夹。 4、运行项目,解读代码结构。 5、【启用OpenAPI支持】→>swagger,在界…...

问题 C: 活动选择
题目描述 学校在最近几天有n个活动,这些活动都需要使用学校的大礼堂,在同一时间,礼堂只能被一个活动使。由于有些活动时间上有冲突,学校办公室人员只好让一些活动放弃使用礼堂而使用其他教室。 现在给出n个活动使用礼堂的起…...
SpringBoot学习(五)-Spring Security配置与应用
注:此为笔者学习狂神说SpringBoot的笔记,其中包含个人的笔记和理解,仅做学习笔记之用,更多详细资讯请出门左拐B站:狂神说!!! Spring Security Spring Security是一个基于Java的开源框架,用于在Java应用程…...

Java解决删除子串后的字符串最小长度
Java解决删除子串后的字符串最小长度 01 题目 给你一个仅由 大写 英文字符组成的字符串 s 。 你可以对此字符串执行一些操作,在每一步操作中,你可以从 s 中删除 任一个 "AB" 或 "CD" 子字符串。 通过执行操作,删除所…...
日志系统一(elasticsearch+filebeat+logstash+kibana)
目录 一、es集群部署 安装java环境 部署es集群 安装IK分词器插件 二、filebeat安装(docker方式) 三、logstash部署 四、kibana部署 背景:因业务需求需要将nginx、java、ingress日志进行收集。 架构:filebeatlogstasheskib…...

游戏版 ChatGPT,要用 AI 角色完善生成工具实现 NPC 自由
微软与 AI 初创公司 Inworld 合作,推出基于 AI 的角色引擎和 Copilot 助理,旨在提升游戏中 NPC 的交互力和生命力,提升游戏体验。Inworld 致力于打造拥有灵魂的 NPC,通过生成式 AI 驱动 NPC 行为,使其动态响应玩家操作…...
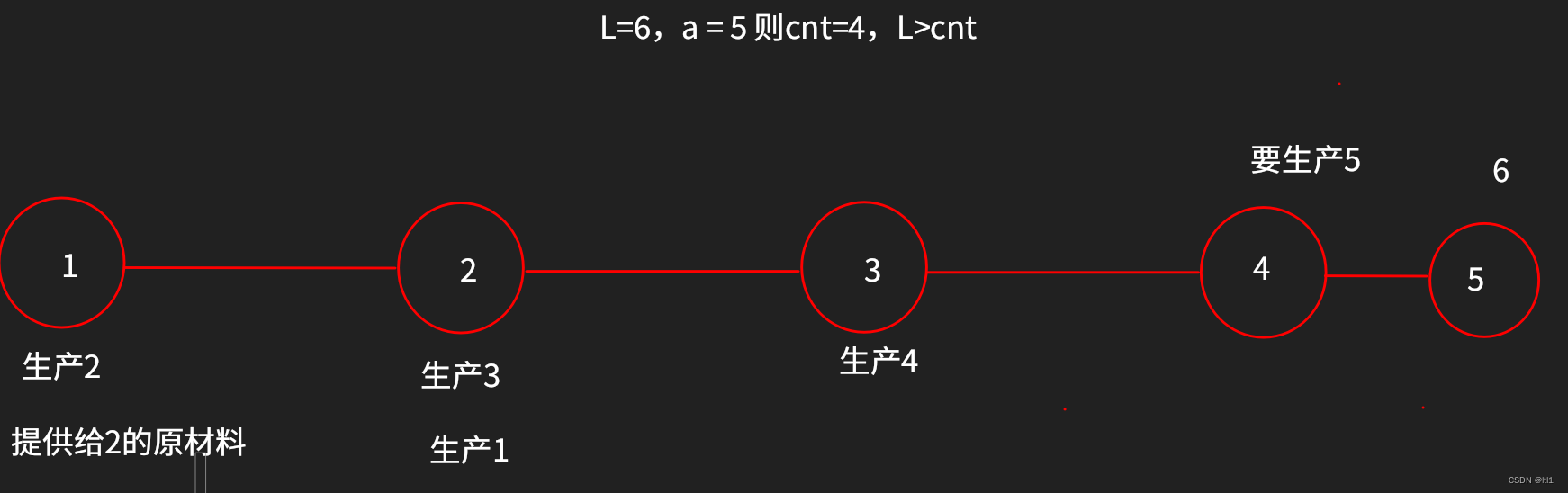
加工零件的题解
目录 原题描述: 题目描述 输入格式 输出格式 样例 #1 样例输入 #1 样例输出 #1 样例 #2 样例输入 #2 样例输出 #2 提示 题目大意: 主要思路: 但是我们怎么才能判断出x走到1时L是偶数还是奇数呢? 初始化:…...
走进shell
Linux系统启动时,会自动创建多个虚拟控制台。虚拟控制台是运行在Linux系统内存中的终端会话。 打开Linux控制台Terminal使用tty命令查看当前使用的虚拟控制台。 注:tty 表示电传打字机(teletypewriter) $ tty /dev/pts/0表示当前使用的是/dev/pts/0 虚拟…...
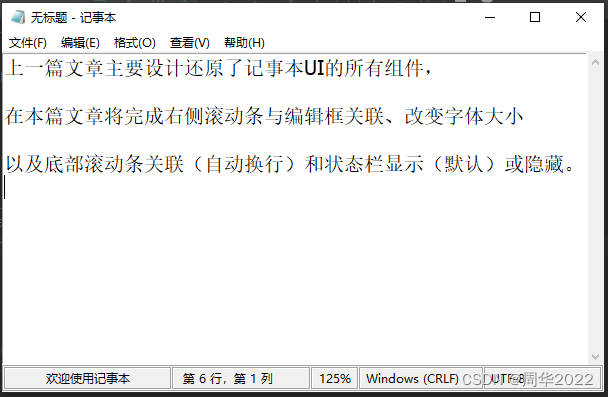
【Python】使用tkinter设计开发Windows桌面程序记事本(2)
上一篇:【Python】使用tkinter设计开发Windows桌面程序记事本(1)-CSDN博客 下一篇: 作者发炎 此代码模块是继承上一篇文章的代码模块的基础上开始设计开发的。 如果不知道怎么新建"记事本项目"文件夹,请参…...
Flutter DateTime 常用处理
今天介绍一下 DateTime 的一些常用功能,对其进行一个整理。 最近在开发过程中好多时候都会使用到时间方面的方法,心想还是统一处理一下,封装一个管理类,这个类可以满足我们开发过程中常用的时间方法。 今天正好整理了一下&#…...

【uniapp】APP打包上架应用商-注意事项
初雪云-uniapp启动图自定义生成(支持一键生成storyboard) HBuilderX需要的自定义storyboard文件格式为 " zip压缩包 " 一、“Android” — 设置targetSdkVersion 小米、OPPO、vivo、华为等主流应用商店,将于2023年12月采用 targetS…...

【算法题】43. 字符串相乘
题目 给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。 注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。 示例 1: 输入: num1 "2", num2 "3…...
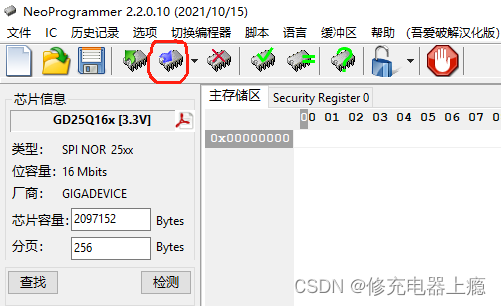
CH341 SPI方式烧录BK7231U
CH341是一个USB总线的转接芯片,通过USB总线提供异步串口、打印口、并口以及常用的2线和4线等同步串行接口。 BK7231U Wi-Fi SOC芯片,内嵌处理器。1. 符合802.11b/g/n 1x1协议 2. 17dBm 输出功率3. 支持20/40 MHz带宽和STBC 4. 支持Wi-Fi STA、AP、…...

sd-webui-EasyPhoto win 安装笔记
目录 安装教程: 插件介绍 ControlNet 1.1 Tile: launch.py问题 依赖库 webui安装问题...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
