Apollo计算几何算法(一)
Planning模块,路径和速度曲线抽象成折线(Polyline),障碍物抽象成多边形(Polygon)。在碰撞检测、投影计算距离、平滑曲线等方面应用广泛。
1 几何算法
1.1 线段
moudles/common/math/line_segment2d.h
namespace apollo {
namespace common {
namespace math {
// 平面线段
class LineSegment2d {public:LineSegment2d();LineSegment2d(const Vec2d &start, const Vec2d &end);// 获取线段的起点const Vec2d &start() const { return start_; }// 获取线段的终点const Vec2d &end() const { return end_; }// 获取从起点到终点的方向const Vec2d &unit_direction() const { return unit_direction_; }// 获取线段的中心Vec2d center() const { return (start_ + end_) / 2.0; }// 旋转线段的终点Vec2d rotate(const double angle);// 返回线段的航向double heading() const { return heading_; }// cos(heading_)double cos_heading() const { return unit_direction_.x(); }// sin(heading_)double sin_heading() const { return unit_direction_.y(); }// 获取线段的长度double length() const;// 获取线段长度的平方double length_sqr() const;/*** @brief Compute the shortest distance from a point on the line segment* to a point in 2-D.* @param point The point to compute the distance to.* @return The shortest distance from points on the line segment to point.*/// 计算线段上的点到2-D中的点的最短距离。double DistanceTo(const Vec2d &point) const;/*** @brief 计算线段上一点到二维中一点的最短距离,得到线段上最近的点* @param point The point to compute the distance to.* @param nearest_pt The nearest point on the line segment* to the input point.* @return 线段上的点到输入点的最短距离*/double DistanceTo(const Vec2d &point, Vec2d *const nearest_pt) const;// 计算线段上的一点到2-D中的一点的最短距离的平方double DistanceSquareTo(const Vec2d &point) const;// 计算二维中线段上一点到一点的最短距离的平方,得到线段上最近的点。double DistanceSquareTo(const Vec2d &point, Vec2d *const nearest_pt) const;/*** @brief 检查一个点是否在线段内* @param point 检查它是否在线段内的点* @return 输入点是否在线段内*/bool IsPointIn(const Vec2d &point) const;// 检查该线段是否与二维中的另一条线段相交bool HasIntersect(const LineSegment2d &other_segment) const;// 计算与二维中另一条线段的交点(如果有的话)bool GetIntersect(const LineSegment2d &other_segment,Vec2d *const point) const;// 计算矢量在线段上的投影double ProjectOntoUnit(const Vec2d &point) const;// 计算向量与线段的叉积double ProductOntoUnit(const Vec2d &point) const;// 计算从线段展开的直线上的二维点的垂直脚部double GetPerpendicularFoot(const Vec2d &point,Vec2d *const foot_point) const;// 获取包含基本信息的调试字符串std::string DebugString() const;private:Vec2d start_;Vec2d end_;Vec2d unit_direction_;double heading_ = 0.0;double length_ = 0.0;
};} // namespace math
} // namespace common
} // namespace apollomoudles/common/math/line_segment2d.cc
计算点到直线的距离
double LineSegment2d::DistanceTo(const Vec2d &point) const {// 如果线段的长度小于等于一个阈值kMathEpsilon,那么点一定在线段上,直接返回点与线段起点的距离if (length_ <= kMathEpsilon) {return point.DistanceTo(start_);}const double x0 = point.x() - start_.x();const double y0 = point.y() - start_.y();// proj,表示点在方向向量上的投影const double proj = x0 * unit_direction_.x() + y0 * unit_direction_.y();// 如果投影小于等于0,说明点在直线段的同侧,直接返回点到线段起点的距离if (proj <= 0.0) {return hypot(x0, y0);}// 如果投影大于等于线段长度,说明点在直线段的延长线上,直接返回点到线段终点的距离if (proj >= length_) {return point.DistanceTo(end_);}return std::abs(x0 * unit_direction_.y() - y0 * unit_direction_.x());
}
给定一个点,计算到线段的最短距离,同时返回最近的点(过给定点的垂线与原线段的交点,或者线段的端点)
double LineSegment2d::DistanceTo(const Vec2d &point,Vec2d *const nearest_pt) const {// 检查nearest_pt是否为空CHECK_NOTNULL(nearest_pt);// 如果线段的长度小于等于一个阈值kMathEpsilon,那么点一定在线段上,直接返回点与线段起点的距离if (length_ <= kMathEpsilon) {*nearest_pt = start_;return point.DistanceTo(start_);}// 计算点与线段起点的坐标差x0和y0const double x0 = point.x() - start_.x();const double y0 = point.y() - start_.y();// 计算proj,表示点在方向向量上的投影const double proj = x0 * unit_direction_.x() + y0 * unit_direction_.y();// 如果投影小于等于0,说明点在直线段的同侧,直接返回点到线段起点的距离。如果投影大于等于线段长度,说明点在直线段的延长线上,直接返回点到线段终点的距离if (proj < 0.0) {*nearest_pt = start_;return hypot(x0, y0);}if (proj > length_) {*nearest_pt = end_;return point.DistanceTo(end_);}*nearest_pt = start_ + unit_direction_ * proj;// 计算点到线段的垂线与x轴正半轴的夹角,即x0 * unit_direction_.y() - y0 * unit_direction_.x(),取绝对值作为最终结果return std::abs(x0 * unit_direction_.y() - y0 * unit_direction_.x());
}
rotate:逆时针旋转angle度(注意是弧度)
Vec2d LineSegment2d::rotate(const double angle) {Vec2d diff_vec = end_ - start_;diff_vec.SelfRotate(angle);return start_ + diff_vec;
}
GetPerpendicularFoot:某个点到该线段垂点的距离
double LineSegment2d::GetPerpendicularFoot(const Vec2d &point,Vec2d *const foot_point) const {CHECK_NOTNULL(foot_point);if (length_ <= kMathEpsilon) {*foot_point = start_;return point.DistanceTo(start_);}const double x0 = point.x() - start_.x();const double y0 = point.y() - start_.y();const double proj = x0 * unit_direction_.x() + y0 * unit_direction_.y();*foot_point = start_ + unit_direction_ * proj;return std::abs(x0 * unit_direction_.y() - y0 * unit_direction_.x());
}
1.2 包围盒
二维平面上,Box特指矩形包围盒。Planning模块经常将自车和障碍物抽象成一个矩形框,简化计算
bounding box
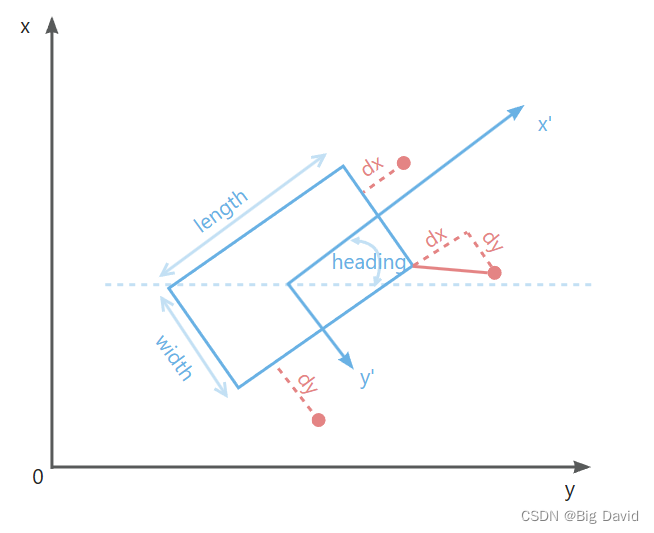
Box2d:普通矩形包围盒
文件路径:modules/common/math/box2d.h
IsPointIn函数检查给定点是否位于由其中心、方向、长度和宽度定义的二维框内
(1)首先计算点相对于长方体中心的x和y分量
(2)然后,它计算点与长方体沿x和y轴的距离,同时考虑长方体的航向。使用航向的余弦和正弦来计算距离。
(3)最后,如果两个距离都小于或等于长方体长度和宽度的一半,加上一个小的ε值(kMathEpsilon),则函数返回true。添加此ε值是为了说明潜在的舍入误差。如果任一距离大于长方体的一半长度或宽度,则函数返回false。
总体思路就是:
(1)以Box的Center为原点,heading方向为X’建立车身坐标系
(2)计算点在车身坐标系下的坐标
假设点的坐标 ( x p , y p ) (x_p,y_p) (xp,yp),Box中心坐标 ( x c , y c ) (x_c,y_c) (xc,yc),Box的heading角度 θ \theta θ,在局部坐标系下的坐标
[ d x d y ] = [ c o s θ s i n θ − s i n θ c o s θ ] [ x p − x 0 y p − y 0 ] \begin{bmatrix} dx\\ dy \end{bmatrix}=\begin{bmatrix} cos\theta & sin\theta\\ -sin\theta &cos\theta \end{bmatrix}\begin{bmatrix} x_p-x_0 \\ y_p-y_0 \end{bmatrix} [dxdy]=[cosθ−sinθsinθcosθ][xp−x0yp−y0]
旋转矩阵是 [ c o s θ − s i n θ s i n θ c o s θ ] \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta &cos\theta \end{bmatrix} [cosθsinθ−sinθcosθ]
(3)判断新坐标的x和y绝对值是否小于半个Box宽度和长度
bool Box2d::IsPointIn(const Vec2d &point) const {const double x0 = point.x() - center_.x();const double y0 = point.y() - center_.y();const double dx = std::abs(x0 * cos_heading_ + y0 * sin_heading_);const double dy = std::abs(-x0 * sin_heading_ + y0 * cos_heading_);return dx <= half_length_ + kMathEpsilon && dy <= half_width_ + kMathEpsilon;
}
判断一个点是否在Boundary上,思路和上面的一样
bool Box2d::IsPointOnBoundary(const Vec2d &point) const {const double x0 = point.x() - center_.x();const double y0 = point.y() - center_.y();const double dx = std::abs(x0 * cos_heading_ + y0 * sin_heading_);const double dy = std::abs(x0 * sin_heading_ - y0 * cos_heading_);return (std::abs(dx - half_length_) <= kMathEpsilon &&dy <= half_width_ + kMathEpsilon) ||(std::abs(dy - half_width_) <= kMathEpsilon &&dx <= half_length_ + kMathEpsilon);
}
double DistanceTo(const Vec2d& point):计算Box到一个点的距离
(1)计算点在局部坐标系下的值
(2)如果 x p ′ x^{'}_p xp′绝对值小于半个车长,则直接用dy作为距离
(3)如果 y p ′ y^{'}_p yp′绝对值小于半个车宽,则直接用dx作为距离
其他情况,返回 d x 2 + d y 2 \sqrt{dx^2+dy^2} dx2+dy2,到角点的距离作为最终的距离
double Box2d::DistanceTo(const Vec2d &point) const {const double x0 = point.x() - center_.x();const double y0 = point.y() - center_.y();const double dx =std::abs(x0 * cos_heading_ + y0 * sin_heading_) - half_length_;const double dy =std::abs(x0 * sin_heading_ - y0 * cos_heading_) - half_width_;if (dx <= 0.0) {return std::max(0.0, dy);}if (dy <= 0.0) {return dx;}return hypot(dx, dy);
}
1.3 多边形
不规则障碍物使用包围盒表示精度低,用多边形Polygon2d来抽象表示。
modules/common/math/polygon2d.h
多边形可以用多个点来表示,也可以用多个边来表示
std::vector<Vec2d> points_;
std::vector<LineSegment2d> line_segments_;
此函数用于从给定的一组点构建多边形
num_points_:多边形中的点数。
points_:Vec2d对象的矢量,表示多边形的点。
area_:多边形的面积。
line_segments_:LineSegment2d对象的矢量,表示连接多边形各点的线段。
is_convex_:一个布尔标志,指示多边形是否是凸的。
min_x_:多边形aabox的最小x值。
max_x_:多边形aabox的最大x值。
min_y_:多边形aabox的最小y值。
max_y_:多边形的aabox的最大y值。
void Polygon2d::BuildFromPoints() {num_points_ = static_cast<int>(points_.size());// 检查点的数量是否至少为3CHECK_GE(num_points_, 3);// 保证点顺时针area_ = 0.0;for (int i = 1; i < num_points_; ++i) {// 使用连接每对点的向量的叉积来计算多边形的面积area_ += CrossProd(points_[0], points_[i - 1], points_[i]);}// 如果面积为负值,则反转点的顺序,以确保它们按顺时针(ccw)顺序排列if (area_ < 0) {area_ = -area_;std::reverse(points_.begin(), points_.end());}area_ /= 2.0;CHECK_GT(area_, kMathEpsilon);// 构建线段line_segments_.reserve(num_points_);// 通过迭代点并将每个点按ccw顺序连接到下一个点来构建线段向量for (int i = 0; i < num_points_; ++i) {line_segments_.emplace_back(points_[i], points_[Next(i)]);}// 检查凸性质is_convex_ = true;for (int i = 0; i < num_points_; ++i) {// 通过计算连接前一点、当前点和下一点的向量的叉积来检查多边形是否是凸,如果叉积小于或等于-kMathEpsilon,则多边形不是凸的if (CrossProd(points_[Prev(i)], points_[i], points_[Next(i)]) <=-kMathEpsilon) {is_convex_ = false;break;}}// 计算aabox.// 最后,它通过找到点的最小值和最大值x和y来计算多边形的轴对齐边界框(aabox)min_x_ = points_[0].x();max_x_ = points_[0].x();min_y_ = points_[0].y();max_y_ = points_[0].y();for (const auto &point : points_) {min_x_ = std::min(min_x_, point.x());max_x_ = std::max(max_x_, point.x());min_y_ = std::min(min_y_, point.y());max_y_ = std::max(max_y_, point.y());}
}
叉积(CrossProd)物理含义是向量组成的平行四边形的面积除以二就是三角形的面积,将所有三角形面积累加可以得到area_,如果area_为负数,说明角点按顺时针(CW)排列,需要进行reverse,从而保证所有的点是逆时针排列的CCW
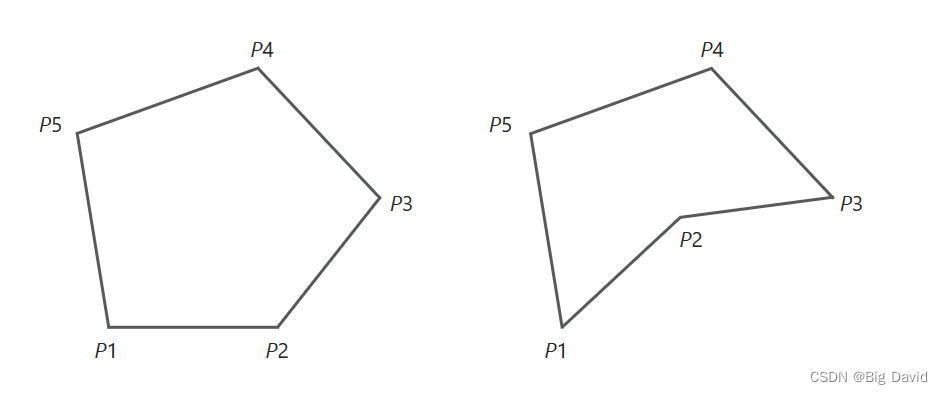
如果连续的三个点 P i − 1 , P i , P i + 1 P_{i-1},P_i,P_{i+1} Pi−1,Pi,Pi+1有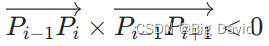
说明多边形非凸,比如右侧就是
相关文章:

Apollo计算几何算法(一)
Planning模块,路径和速度曲线抽象成折线(Polyline),障碍物抽象成多边形(Polygon)。在碰撞检测、投影计算距离、平滑曲线等方面应用广泛。 1 几何算法 1.1 线段 moudles/common/math/line_segment2d.h n…...

计算机网络、浏览器相关高频面试题
为什么使用CDN 会更快? 没有使用CDN的情况下,用户从浏览器输入地址,依次经过浏览器缓存、操作系统缓存(如本地host文件)、域名解析服务器、根域名解析服务器、顶级域名服务器直到找到对应的ip地址返回给用户ÿ…...

遥感单通道图像保存为彩色图像
系列文章目录 第一章PIL单通道图像处理 文章目录 系列文章目录前言一、代码实现二、问题记录在这里插入图片描述 总结 前言 将单通道图像以彩色图像的形式进行保存主要使用了PIL库 一、代码实现 palette_data [***]:可以进行自定义设置 代码如下: fr…...
如何将字符串转换为整数
将字符串转换为整数是常见的编程需求。以下是几种常见编程语言的示例: Python str_num "123" num int(str_num) print(num) # 输出: 123 JavaScript let str_num "123"; let num parseInt(str_num); console.log(num); // 输…...

如何在Linux上安装使用达芬奇DaVinci-Resolve视频剪辑|附带格式转换脚本
如何在openSUSE-Linux上安装DaVinci-Resolve 您是否还在等待Adobe套件在Linux上的到来?您是否曾多次尝试通过Wine使用Premiere?您是否还在想苹果为什么不以Linux本机版本发布Final Cut Pro? 如果您对所有这些问题中的一个或全部回答是&…...
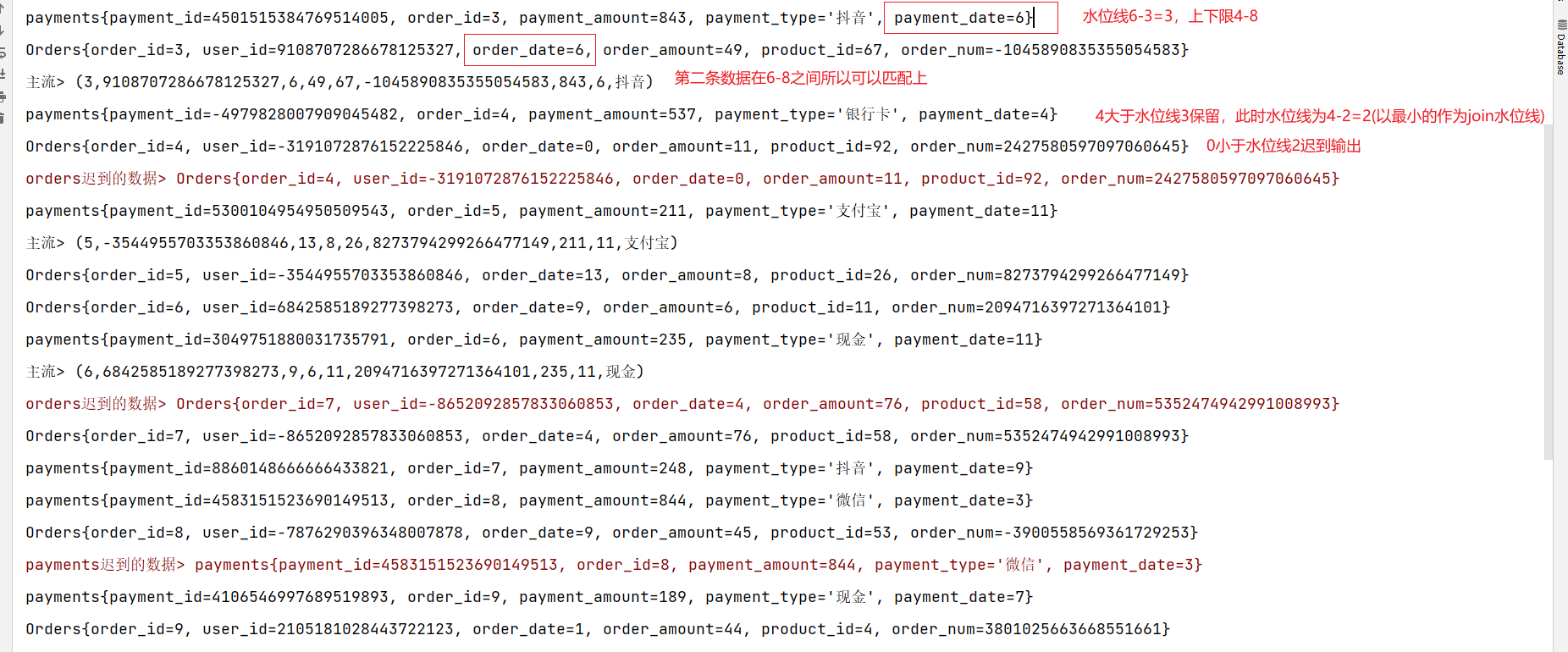
FlinkAPI开发之数据合流
案例用到的测试数据请参考文章: Flink自定义Source模拟数据流 原文链接:https://blog.csdn.net/m0_52606060/article/details/135436048 概述 在实际应用中,我们经常会遇到来源不同的多条流,需要将它们的数据进行联合处理。所以…...
11 个 Python全栈开发工具集
前言 以下是专注于全栈开发不同方面的 Python 库;有些专注于 Web 应用程序开发,有些专注于后端,而另一些则两者兼而有之。 1. Taipy Taipy 是一个开源的 Python 库,用于构建生产就绪的应用程序前端和后端。 它旨在加快应用程序开发…...
【GDAL】Windows下VS+GDAL开发环境搭建
Step.0 环境说明(vs版本,CMake版本) 本地的IDE环境是vs2022,安装的CMake版本是3.25.1。 Step.1 下载GDAL和依赖的组件 编译gdal之前需要安装gdal依赖的组件,gdal所依赖的组件可以在官网文档找到,可以根据…...

基于sumo实现交通灯控制算法的模板
基于sumo实现交通灯控制算法的模板 目录 在windows安装run hello world networkroutesviewsettings & configurationsimulation 交通灯控制系统 介绍文件生成器类(FileGenerator)道路网络(Network)辅助函数生成道路网络&am…...

设计模式之单例模式的懒饿汉
懒汉式 说白了就是你不叫我我不动,你叫我我才动。 类初始化模式,也叫延迟占位模式。在单例类的内部由一个私有静态内部类来持有这个单例类的实例。因为在 JVM 中,对类的加载和类初始化,由虚拟机保证线程安全。 public class Singl…...

多平台多账号一站式短视频管理矩阵营销系统下载
矩阵营销系统多平台多账号一站式管理,一键发布作品。智能标题,关键词优化,排名查询,混剪生成原创视频,账号分组,意向客户自动采集,智能回复,多账号评论聚合回复,免切换&a…...

go work
vscode gopls插件工具依赖go work,否则会报错 https://github.com/golang/tools/blob/master/gopls/doc/workspace.md Go 1.18 新特性多模块工作区教程-让多模块开发变得简单 - Go语言中文网 - Golang中文社区...
基于JavaWeb+BS架构+SpringBoot+Vue智能菜谱推荐系统的设计和实现
基于JavaWebBS架构SpringBootVue智能菜谱推荐系统的设计和实现 文末获取源码Lun文目录前言主要技术系统设计功能截图订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 文末获取源码 Lun文目录 目 录 目 录 III 第一章 概述 1 1.1 研究背景 1 1.2研究目的及意义 1 1.3…...
SpringSecurity集成JWT实现后端认证授权保姆级教程-授权配置篇
🍁 作者:知识浅谈,CSDN签约讲师,CSDN博客专家,华为云云享专家,阿里云专家博主 📌 擅长领域:全栈工程师、爬虫、ACM算法 💒 公众号:知识浅谈 🔥网站…...

关系型非关系型数据库区别,以MongoDB为例在express中连接MongoDB示例
目录 关系型数据库 关系型数据库常见的类型有: 关系型数据库的优点包括: 非关系型数据库 非关系型数据库常见的类型有: 非关系型数据库的特点包括: 关系型数据库和非关系型数据库区别 MongoDB是什么 MongoDB优势ÿ…...
Java版商城:Spring Cloud+SpringBoot b2b2c实现多商家入驻直播带货及 免 费 小程序商城搭建的完整指南
随着互联网的快速发展,越来越多的企业开始注重数字化转型,以提升自身的竞争力和运营效率。在这个背景下,鸿鹄云商SAAS云产品应运而生,为企业提供了一种简单、高效、安全的数字化解决方案。 鸿鹄云商SAAS云产品是一种基于云计算的软…...
【Spring Boot】SpringBoot maven 项目创建图文教程
创建一个Spring Boot项目并使用Maven进行构建是一项相对简单的任务。以下是使用IntelliJ IDEA创建Spring Boot Maven项目的详细教程: 步骤 1:安装 IntelliJ IDEA 确保你已经安装了最新版本的 IntelliJ IDEA。你可以从官方网站下载并安装。 步骤 2&am…...
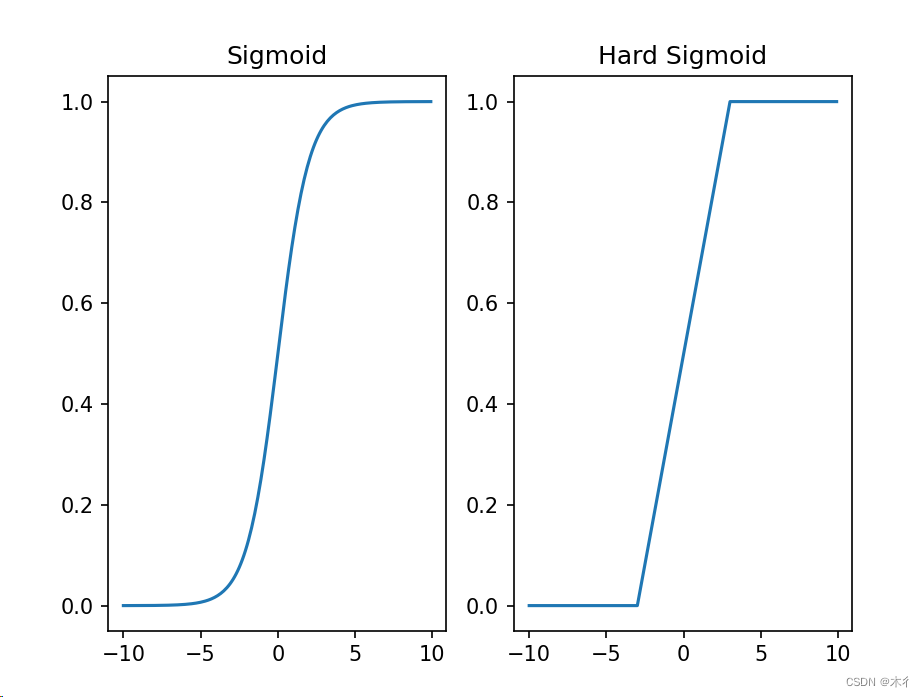
【Python】Sigmoid和Hard Sigmoid激活函数对比总结及示例
Sigmoid和Hard Sigmoid是两种常用的激活函数,它们在神经网络中起到非线性变换的作用。以下是它们之间的对比和优缺点总结: Sigmoid激活函数: 优点: 输出范围是0到1之间,可以用于二分类问题。函数形状相对平滑&#…...

ajax+axios——统一设置请求头参数——添加请求头入参——基础积累
最近在写后台管理系统(我怎么一直都只写管理系统啊啊啊啊啊啊啊),遇到一个需求,就是要在原有系统的基础上,添加一个仓库的切换,并且需要把选中仓库对应的id以请求头参数的形式传递到每一个接口当中。。。 …...
Redis高可用(主从复制、哨兵模式和Cluster集群)
目录 前瞻 主从复制 哨兵 集群 主从复制 主从复制的作用 主从复制流程 搭建Redis主从复制 实验准备 实验流程 修改 Redis 配置文件(Master节点操作) 修改 Redis 配置文件(Slave节点操作) 验证主从效果 哨兵模式 哨兵…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
