剑指 Offer II 012. 左右两边子数组的和相等
题目链接
剑指 Offer II 012. 左右两边子数组的和相等 easy
题目描述
给你一个整数数组 nums,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1。
示例 1:
输入:nums = [1,7,3,6,5,6]
输出:3
解释:
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1]
输出:0
解释:
中心下标是 0 。
左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
提示:
- 1<=nums.length<=1041 <= nums.length <= 10^41<=nums.length<=104
- −1000<=nums[i]<=1000-1000 <= nums[i] <= 1000−1000<=nums[i]<=1000
分析:
对于原数组 nums[0 , n-1]区间,我们用前缀和数组 s[0 , n]来表示其前缀和,即:
- s[0]=0s[0] = 0s[0]=0
- s[1]=nums[0]s[1] = nums[0]s[1]=nums[0]
- s[2]=nums[0]+nums[1]s[2] = nums[0] + nums[1]s[2]=nums[0]+nums[1]
- s[3]=nums[0]+nums[1]+nums[2]s[3] = nums[0] + nums[1] + nums[2]s[3]=nums[0]+nums[1]+nums[2]
- …
那么对于 下标i,我们就能快速的得出它两边的和 leftsum = s[i-1],rightsum = s[n] - s[i]。我们只需要判断这两部分是否相等即可。
时间复杂度: O(n)O(n)O(n)
C++代码:
class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> s(n+1);for(int i = 1;i <= n;i++) s[i] = s[i-1] + nums[i-1];for(int i = 1;i <= n;i++){if(s[i-1] == s[n] - s[i]) return i - 1;}return -1;}
};
Java代码:
class Solution {public int pivotIndex(int[] nums) {int n = nums.length;int[] s = new int[n+1];for(int i = 1;i <= n;i++) s[i] = s[i-1] + nums[i-1];for(int i = 1;i <= n;i++){if(s[i-1] == s[n] - s[i]) return i - 1;}return -1;}
}相关文章:

剑指 Offer II 012. 左右两边子数组的和相等
题目链接 剑指 Offer II 012. 左右两边子数组的和相等 easy 题目描述 给你一个整数数组 nums,请计算数组的 中心下标 。 数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。 如果中心下标位于数组最左端,那…...

Java货物摆放
题目描述 小蓝有一个超大的仓库,可以摆放很多货物。 现在,小蓝有 � n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。 小蓝希望所…...

计算机求解满足三角形各边数字之和相等的数字填充
圆圈处不重复的填入1至9,使得每条边的四个数字相加的总和相等。 求解思路: 数组中存放1到9的数字,每次随机交换两个数字,构建出新的数字组合,计算这个数字组合是否符合要求。 #include <stdio.h> #include <…...

python魔术方法
魔术方法 魔术方法就是一个类中的方法,和普通方法唯一的不同是普通方法需要调用,而魔术方法是在特定时刻自动触发。这些魔术方法的名字特定,不能更改,但是入口参数的名字可以自己命名。 基本魔术方法 new(cls[,…]) _new_ 是在…...

从0开始学python -48
Python CGI编程-3 CGI中使用Cookie 在 http 协议一个很大的缺点就是不对用户身份的进行判断,这样给编程人员带来很大的不便, 而 cookie 功能的出现弥补了这个不足。 cookie 就是在客户访问脚本的同时,通过客户的浏览器,在客户硬…...

当面试官问我前端可以做的性能优化有哪些
面试过程中面试官问到前端性能优化有哪些,当我咔咔一顿输出之后面试官追问:前端可以做的性能优化有哪些呢? 前端优化大概可以有以下几个方向: 网络优化页面渲染优化JS优化图片优化webpack打包优化React优化Vue优化 网络优化 D…...

一文读懂Java/O流的使用方法和技巧
1.前言 Java 中的 I/O 流是实现输入和输出的一种机制,可以用来读写文件、网络、内存等各种资源。Java 提供了各种类型的流,包括字节流和字符流,以及面向文本和二进制数据的流。在本文中,我们将深入探讨 Java I/O 流的各个方面&am…...

AI for Science系列(二):国内首个基于AI框架的CFD工具组件!赛桨v1.0 Beta API介绍以及典型案例分享!
AI for Science被广泛认为是下一代科研范式,可以有效处理多维度、多模态、多场景下的模拟和真实数据,解决复杂推演计算问题,加速新科学问题发现[1] 。百度飞桨科学计算工具组件赛桨PaddleScience是国内首个公开且可应用于CFD(Comp…...
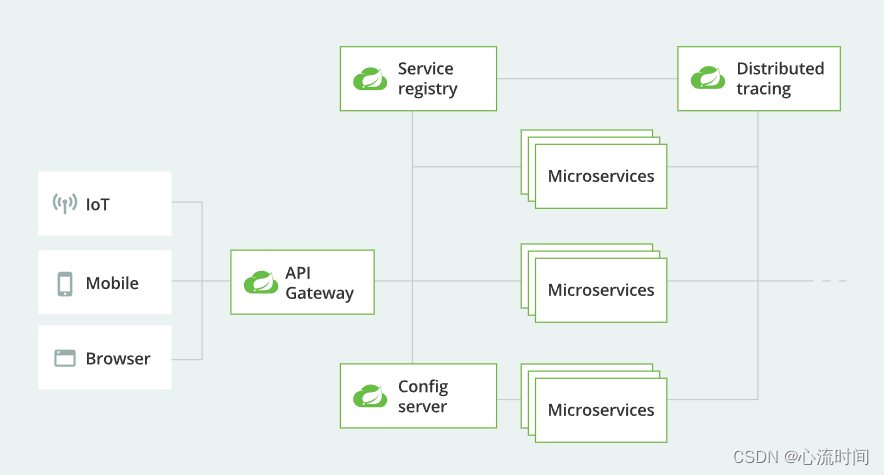
SpringCloud简单介绍
文章目录1. 开源组件2. CAP原则1. 开源组件 功能springcloud netflixspringcloud alibabaspringcloud官方其他服务注册与发现eurekanacosconsulzookeeper负载均衡ribbondubbo服务调用openFeigndubbo服务容错hystrixsentinel服务网关zuulgateway服务配置的同一管理cofig-server…...
《uniapp基础知识》学习笔记Day38-(Period2)全局文件一些常用的配置
如果进行开发的话,首先要配置路由页面 page.json 页面路由 pages.json 文件用来对 uni-app 进行全局配置,决定页面文件的路径、窗口样式、原生的导航栏、底部的原生tabbar 等。 {"pages": [{"path": "pages/component/index…...

APICloud 弹动与滚轴冲突的解决模拟
当打开页面的bounces开关来实现下拉刷新和上翻加载是,如果页面中有scroll-view,那么手指上下滑动时弹动会触发,而滚轴无法正常实现,只有按住不动再拖动滚轴才会触发。开始想通过获取手指点击屏幕的坐标点设置触发条件来解决两者的…...

Spring Cloud(微服务)学习篇(四)
Spring Cloud(微服务)学习篇(四) 1.nacos实现服务之间传参数 1.1 在dto包(shop-sms-api项目)中创建SmsDTO类 package com.zlz.shop.sms.api.dto;import lombok.Data;Data public class SmsDTO {private String tel; }1.2 复制SmsDTO类到shop-sms-server项目的dto包下面 1.3 …...

【Java Pro】001-Java基础:面向对象
【Java Pro】001-Java基础:面向对象 文章目录【Java Pro】001-Java基础:面向对象一、面向对象1、什么是对象现实生活中的对象与程序中的对象2、什么是面向对象面向过程面向对象3、面向过程与面向对象的比较思想方面设计方式方面实现方式方面4、面向过程与…...

ElasticSearch从0到1——基础知识
1.ES是什么? 是一个开源的高扩展的分布式全文检索引擎,它可以近乎实时的存储、检索数据;本身扩展性很好,可以扩展到上百台服务器,处理PB级别的数据使用Java开发并使用Lucene作为其核心来实现所有索引和搜索的功能&…...

【面试系列】equals和==的区别
问题:两个对象值相同(x.equals(y) true),但是可能存在hashCode不同吗? 的定义 比较的是两个对象的内存地址,相等则意味着内存地址一样。 对象的equals方法 Object#equals public boolean equals(Object obj) {return (this obj);}Stri…...

存在重复元素模块-三道题
文章目录存在重复元素217. 存在重复元素219. 存在重复元素 II220. 存在重复元素 III (SortedList二分)小结存在重复元素 217. 存在重复元素 题目链接:217. 存在重复元素 题目大意:给你一个整数数组 nums 。如果任一值在数组中出…...

3种方法删除7-Zip压缩包的密码
7-Zip压缩软件是一款完全免费且开源的软件,不仅能压缩和解压7-Zip压缩包,还能给压缩包设置打开密码。 有些小伙伴可能会遇到这样的问题,7-Zip压缩包设置密码后,过了一段时间不需要密码保护了,或者一不小心忘记了密码&…...

Codeforces Round 855 (Div. 3)(A~F)
A. Is It a Cat?定义满足条件的字符串为:其中仅可能含有meow四种字母的大小写,而且相同种类的字母必须挨在一起,四种字母的顺序必须按照meow排列。给出一个字母串,求是否满足条件。思路:感觉是个很麻烦的模拟。首先把…...
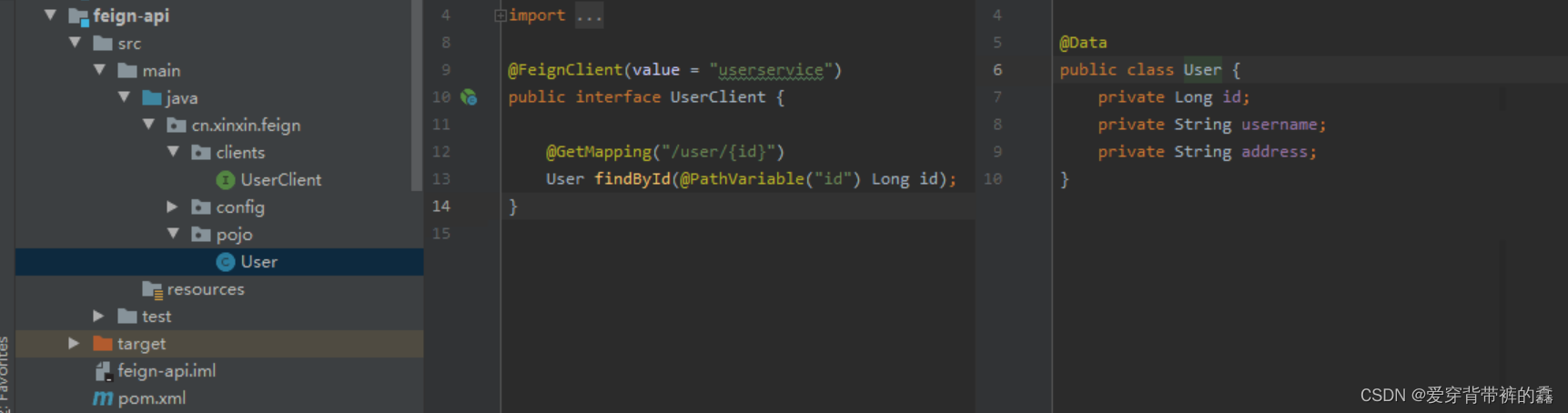
【SpringCloud】SpringCloud详解之Feign实战
目录前言SpringCloud Feign远程服务调用一.需求二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用(order服务内编写)四.使用Feign远程调用(order服务内配置)五.自定义Feign配置(order服务内配置)六.Feign配置日志(oder服务内配置)七.Feign调优(order服务内配置)八.抽…...

tuts4you上lena‘s40个crackme(1)
本来是不打算写文章了,因为懒,想以后通过录屏的形式保存一下自己学的路程。但奈何开学后一直没找到机会,在宿舍也不愿意大吼大叫的讲东西,只好再写写文章了 最近学了一些汇编语言和逆向工程,所以就想通过这40给题目来看…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
