平面光波导_三层均匀平面光波导_射线分析法
平面光波导_三层均匀平面光波导_射线分析法
三层均匀平面光波导:
- 折射率沿 x x x 方向有变化,沿 y y y、 z z z 方向没有变化
- 三层:芯区( n 1 n_1 n1) > > > 衬底( n 2 n_2 n2) ≥ \geq ≥ 包层( n 3 n_3 n3)
- 包层通常为空气,即 n 3 = 1 n_3=1 n3=1;芯区与衬底折射率之差通常为 1 0 − 3 ∼ 1 0 − 1 10^{-3}\sim 10^{-1} 10−3∼10−1;芯区一般几微米厚
一、三层均匀平面波导的射线分析法
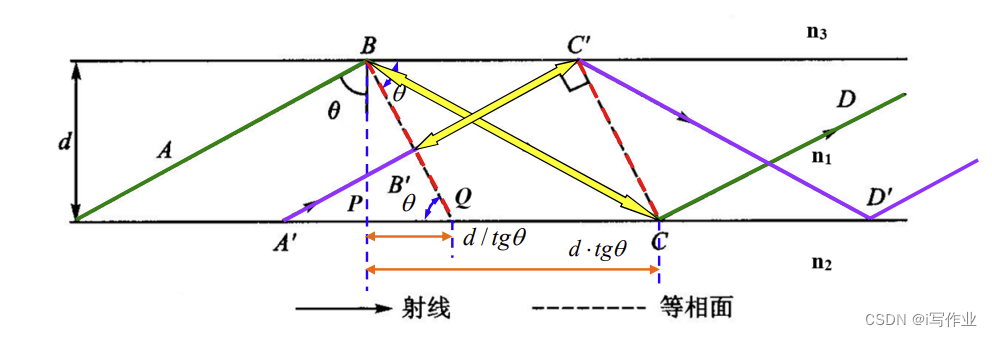
三层均匀平面波导的传输路线(也是叠加模型)如上图所示:
- 它可以看作由斜着向上界面行进的平面波(以 B B ′ BB^\prime BB′ 为等相位面的平面波),与反射2次后再次斜向上运动的平面波(以 C C ′ CC^\prime CC′ 为等相位面的平面波)相互叠加而成
- 入射光满足全反射条件仅仅能使光被约束在波导中,是形成导波的必要条件(还有是否可以传输)
- 因为导波由2个平面波相叠加,所以当两平面波到达同一地点时,只有满足相位相同的条件,才会相干相长,维持光在波导中传播。否则会相互抵消,导致无法传播
传输条件——相干叠加条件的推导:
约束条件: A B − A ′ B ′ AB-A^\prime B^\prime AB−A′B′ 平面波(以 B B ′ BB^\prime BB′ 为等相位面的平面电磁波)向前传播,第一个发生第二次反射的点( C C C 点)其发生全反射相移后仍应与前一入射平面波保持同相。
记全反射在两界面带来的相移分别为: − 2 ϕ 12 -2\phi_{12} −2ϕ12、 − 2 ϕ 13 -2\phi_{13} −2ϕ13
因为 B B ′ BB^\prime BB′、 C C ′ CC^\prime CC′ 是等相位面,需要 A B A ′ B ′ ABA^\prime B^\prime ABA′B′ 平面波与 C D C ′ D ′ CDC^\prime D^\prime CDC′D′ 平面波相干相长,因此计算 B ′ C ′ B^\prime C^\prime B′C′ 和 B C BC BC 分别带来的光程,且两光程差应为 2 π 2\pi 2π 的整数倍
其中入射光的初始状况、三层均匀平面波导的各层折射率、波导芯区厚度是易于获取的参数,各表达式最终应当尽可能使用这三类参数表达
-
B ′ → C ′ B^\prime\to C^\prime B′→C′ 的光程: n 1 B ′ C ′ ‾ = n 1 B C ′ ‾ sin θ = n 1 ( P C ‾ − P Q ‾ ) sin θ = n 1 ( d tan θ − d / tan θ ) sin θ n_1\overline{B^\prime C^\prime}=n_1\overline{BC^\prime}\sin\theta=n_1(\overline{PC}-\overline{PQ})\sin\theta=n_1\left( d\tan\theta-d/\tan\theta \right)\sin\theta n1B′C′=n1BC′sinθ=n1(PC−PQ)sinθ=n1(dtanθ−d/tanθ)sinθ
其总相移为: k 0 n 1 ( d tan θ − d / tan θ ) sin θ k_0n_1\left( d\tan\theta-d/\tan\theta \right)\sin\theta k0n1(dtanθ−d/tanθ)sinθ
-
B → C B\to C B→C 的光程: n 1 B C ‾ = n 1 ⋅ d / cos θ n_1\overline{BC}=n_1\cdot d/\cos\theta n1BC=n1⋅d/cosθ
其在界面 1,2 和界面 1,3 分别发生了一次全反射,带来的相移为 − 2 ϕ 12 − 2 ϕ 13 -2\phi_{12}-2\phi_{13} −2ϕ12−2ϕ13
其总相移为: k 0 n 1 ⋅ d / cos θ − 2 ϕ 12 − 2 ϕ 13 k_0n_1\cdot d/\cos\theta-2\phi_{12}-2\phi_{13} k0n1⋅d/cosθ−2ϕ12−2ϕ13
此时两平面波相干相长即要求:
k 0 n 1 ⋅ d / cos θ − 2 ϕ 12 − 2 ϕ 13 − k 0 n 1 ( d tan θ − d / tan θ ) sin θ = 2 m π m = 0 , 1 , 2 , ⋯ k_0n_1\cdot d/\cos\theta-2\phi_{12}-2\phi_{13}-k_0n_1\left( d\tan\theta-d/\tan\theta \right)\sin\theta=2m\pi\quad m=0,1,2,\cdots k0n1⋅d/cosθ−2ϕ12−2ϕ13−k0n1(dtanθ−d/tanθ)sinθ=2mπm=0,1,2,⋯
此式只与三层平面均匀波导的厚度、折射率,入射光的入射角、波数有关;其分立的解对应导波的不同模式
将上式简记为:
κ d = m π + ϕ 12 + ϕ 13 (模式的本征方程/特征方程) \kappa d=m\pi+\phi_{12}+\phi_{13} \tag{模式的本征方程/特征方程} κd=mπ+ϕ12+ϕ13(模式的本征方程/特征方程)
-
κ = k x = n 1 k 0 cos θ = n 1 2 k 0 2 − β 2 = k 0 n 1 2 − N 2 \kappa=k_x=n_1k_0\cos\theta=\sqrt{n_1^2k_0^2-\beta^2}=k_0\sqrt{n_1^2-N^2} κ=kx=n1k0cosθ=n12k02−β2=k0n12−N2
-
模折射率/有效折射率: N = β / k 0 N=\beta/k_0 N=β/k0
-
β \beta β 为传播常数。通过模式的本征方程/特征方程可以求出不同模式的传播常数
对于 TE、TM,其全反射相移公式为:
r T E = E ⃗ 0 ′ E ⃗ 0 = n 1 cos θ 1 − n 2 2 − n 1 2 s i n 2 θ 1 n 1 cos θ 1 + n 2 2 − n 1 2 s i n 2 θ 1 = e x p [ − j 2 arctan ( n 1 2 sin 2 θ 1 − n 2 2 n 1 cos θ 1 ) ] = e − j 2 ϕ T E r_{TE}=\frac{\vec E_0^\prime}{\vec E_0}=\frac {n_1\cos\theta_1-\sqrt{n_2^2-n_1^2sin^2\theta_1}} {n_1\cos\theta_1+\sqrt{n_2^2-n_1^2sin^2\theta_1}} =exp\left[ {-j2\arctan\left( \frac{\sqrt{n_1^2\sin^2\theta_1-n_2^2}}{n_1\cos\theta_1} \right)} \right] =e^{-j2\phi_{TE}} rTE=E0E0′=n1cosθ1+n22−n12sin2θ1n1cosθ1−n22−n12sin2θ1=exp −j2arctan n1cosθ1n12sin2θ1−n22 =e−j2ϕTE
r T M = H ⃗ 0 ′ H ⃗ 0 = n 2 2 cos θ 1 − n 1 n 2 2 − n 1 2 s i n 2 θ 1 n 2 2 cos θ 1 + n 1 n 2 2 − n 1 2 s i n 2 θ 1 = e x p [ − j 2 arctan ( n 1 2 n 2 2 n 1 2 sin 2 θ 1 − n 2 2 n 1 cos θ 1 ) ] = e − j 2 ϕ T M r_{TM}=\frac{\vec H_0^\prime}{\vec H_0}=\frac {n_2^2\cos\theta_1-n_1\sqrt{n_2^2-n_1^2sin^2\theta_1}} {n_2^2\cos\theta_1+n_1\sqrt{n_2^2-n_1^2sin^2\theta_1}} =exp\left[ {-j2\arctan\left( \frac{n_1^2}{n_2^2}\frac{\sqrt{n_1^2\sin^2\theta_1-n_2^2}}{n_1\cos\theta_1} \right)} \right] =e^{-j2\phi_{TM}} rTM=H0H0′=n22cosθ1+n1n22−n12sin2θ1n22cosθ1−n1n22−n12sin2θ1=exp −j2arctan n22n12n1cosθ1n12sin2θ1−n22 =e−j2ϕTM
可以简记为:
T E m o d e { ϕ 12 = arctan ( P κ ) ϕ 13 = arctan ( q κ ) T M m o d e { ϕ 12 = arctan ( n 1 2 n 2 2 P κ ) ϕ 13 = arctan ( n 1 2 n 3 2 q κ ) TE\ mode \begin{cases} \phi_{12}=\arctan\left( \frac P\kappa \right) \\\\ \phi_{13}=\arctan\left( \frac q\kappa \right) \\ \end{cases} \\\\ TM\ mode \begin{cases} \phi_{12}=\arctan\left( \frac{n_1^2}{n_2^2} \frac P\kappa \right) \\\\ \phi_{13}=\arctan\left( \frac{n_1^2}{n_3^2} \frac q\kappa \right) \\ \end{cases} \\ TE mode⎩ ⎨ ⎧ϕ12=arctan(κP)ϕ13=arctan(κq)TM mode⎩ ⎨ ⎧ϕ12=arctan(n22n12κP)ϕ13=arctan(n32n12κq)
其本征方程为:
T E : κ d = m π + arctan ( P κ ) + arctan ( q κ ) T M : κ d = m π + arctan ( n 1 2 n 2 2 P κ ) + arctan ( n 1 2 n 3 2 q κ ) TE:\kappa d=m\pi+\arctan\left( \frac P\kappa \right)+\arctan\left( \frac q\kappa \right) \\\\ TM:\kappa d=m\pi+\arctan\left( \frac{n_1^2}{n_2^2} \frac P\kappa \right)+\arctan\left( \frac{n_1^2}{n_3^2} \frac q\kappa \right) TE:κd=mπ+arctan(κP)+arctan(κq)TM:κd=mπ+arctan(n22n12κP)+arctan(n32n12κq)
相关文章:

平面光波导_三层均匀平面光波导_射线分析法
平面光波导_三层均匀平面光波导_射线分析法 三层均匀平面光波导: 折射率沿 x x x 方向有变化,沿 y y y、 z z z 方向没有变化三层:芯区( n 1 n_1 n1) > > > 衬底( n 2 n_2 n2) ≥ \geq ≥ 包层( n 3 n_3 n3)包层通常为空…...

IPV6学习记录
IPV6的意义 从广义上来看IPV6协议包含的内容很多: IPV6地址的生成与分配 IPV6的报头的功能内容 IPV4网络兼容IPV6的方案 ICMPv6的功能(融合了arp和IGMP功能) IPV6的路由方式 ipv6的诞生除了由于ipv4的地址枯竭外,很大程度上也是因为ipv4多年的发展产生了很多…...

使用proteus进行主从JK触发器仿真失败原因的分析
在进行JK触发器的原理分析的时候,我首先在proteus根据主从JK触发器的原理进行了实验根据原理图,如下图: 我进行仿真,在仿真的过程中,我向电路图中添加了外部的置0/1端口,由此在proteus中得到下面的电路图 …...
Golang基础入门及Gin入门教程(2024完整版)
Golang是Google公司2009年11月正式对外公开的一门编程语言,它不仅拥有静态编译语言的安全和高性能,而 且又达到了动态语言开发速度和易维护性。有人形容Go语言:Go C Python , 说明Go语言既有C语言程序的运行速度,又能达到Python…...
等级考试试卷(四级)电子学会真题)
202312 青少年软件编程(C/C++)等级考试试卷(四级)电子学会真题
2023年12月 青少年软件编程(C/C)等级考试试卷(四级)电子学会真题 1.移动路线 题目描述 桌子上有一个m行n列的方格矩阵,将每个方格用坐标表示,行坐标从下到上依次递增,列坐标从左至右依次递增…...

leetcode-合并两个有序数组
88. 合并两个有序数组 题解: 这是一个经典的双指针问题,我们可以使用两个指针分别指向nums1和nums2的最后一个元素,然后比较两个指针所指向的元素大小,将较大的元素放入nums1的末尾,并将对应的指针向前移动一位。重复…...
网站怎么做google搜索引擎优化?
网站想做google搜索引擎优化,作为大前提,您必须确保网站本身符合google规范,我们不少客户实际上就连这点都无法做到 有不少客户公司自己本身有技术,就自己弄一个网站出来,做网站本身不是难事,但前提是您需要…...

TDengine 签约西电电力
近年来,随着云计算和物联网技术的迅猛发展,传统电力行业正朝着数字化、信息化和智能化的大趋势迈进。在传统业务基础上,电力行业构建了信息网络、通信网络和能源网络,致力于实现发电、输电、变电、配电和用电的实时智能联动。在这…...

赛门铁克OV代码签名证书一年多少钱?
在当前,软件和应用程序的安全性变得尤为重要。为了保护软件的完整性和安全性,越来越多的开发者和厂商开始采用代码签名的方式来确保软件的真实性和完整性。赛门铁克OV代码签名证书成为了其中一个备受信任的选择。那么,赛门铁克OV代码签名证书…...

Dockerfile详解
文章目录 一、Dockerfile介绍二、常用指令三、Dockerfile示例四、最佳实践 一、Dockerfile介绍 Dockerfile是一个包含创建镜像所有命令的文本文件,通过docker build命令可以根据Dockerfile的内容构建镜像。 一般的,Dockerfile分为四部分:基础…...
零基础小白如何自学sql?
学习SQL对于数据分析和处理来说非常重要。SQL是一种强大的工具,可以帮助你与数据库沟通,提取,整理和理解数据。 以下是一些学习SQL的建议: 01 前期:SQL数据库学习 了解SQL的基本概念:首先,你…...

【刷题笔记2】
刷题笔记2 最小公倍数、最大公约数 两个数的最大公约数两数乘积/最小公倍数 #<include> cmath; int a,b; int mgcd(a,b);//求最大公约数复制字符串substr()函数 s.substr(pos, len) :pos的默认值是0,len的默认值是s.size() - pos string a1;in…...

Kafka之集群搭建
1. 为什么要使用kafka集群 单机服务下,Kafka已经具备了非常高的性能。TPS能够达到百万级别。但是,在实际工作中使用时,单机搭建的Kafka会有很大的局限性。 消息太多,需要分开保存。Kafka是面向海量消息设计的,一个T…...

Linux备忘手册
常⽤命令 作⽤ shutdown -h now 即刻关机 shutdown -h 10 10分钟后关机 shutdown -h 11:00 11:00关机 shutdown -h 10 预定时间关机(10分钟后) shutdown -c 取消指定时间关机 shutdown -r now 重启 shutdown -r 10 10分钟之后重启 shutdown -…...

Qt中QGraphicsView总体架构学习
前沿 前段时间学习了下如何在QGraphicsView架构中绘制刻度尺,主要是与OnPainter中进行比较的,那么今天就来详细讲解下我对QGraphicsView框架的认知吧~ 最近一段时间想学习下,如果我有不正确的,欢迎留言探讨哟~ QGraphicsView架…...
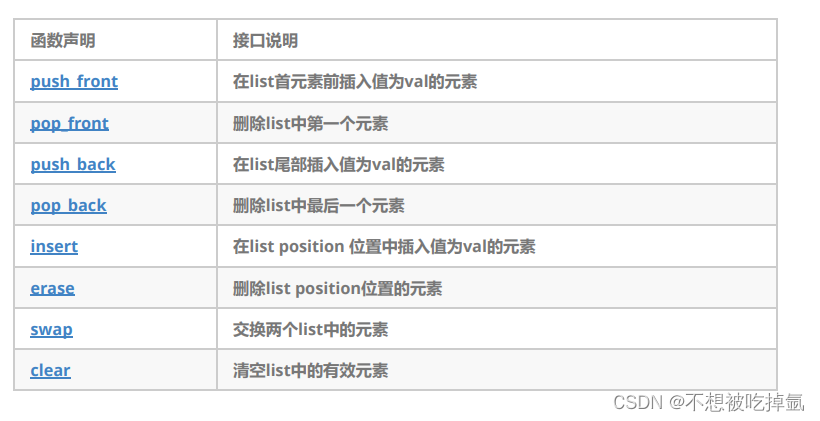
STL-list的使用简介
目录 编辑 一、list的底层实现是带头双向循环链表 二、list的使用 1、4种构造函数(与vector类似)编辑 2、迭代器iterator 3、容量(capicity)操作 4、element access 元素获取 5、增删查改 list modifiers 6、list的迭…...

MySQL:索引失效场景总结
1 执行计划查索引 通过执行计划命令可以查看查询语句使用了什么索引。 EXPLAIN SELECT * FROM ods_finebi_area WHERE areaName = 福建 执行查询计划后,key列的值就是被使用的索引的名称,若key列没有值表示查询未使用索引。 2 在什么列上创建索引 (1)列经常被用于where…...

LNMP平台对接redis服务
目录 1、安装 LNMP 各个组件 2、安装 redis 服务 3、安装 redis 扩展 4、修改 php 配置文件 5、测试连接 1、安装 LNMP 各个组件 2、安装 redis 服务 3、安装 redis 扩展 官网:http://redis.io/ 下载包: https://codeload.github.com/phpredis/p…...
5G之味,在烟火长沙
今年夏天,有一部电影叫做《长沙夜生活》。影片讲述了长沙大排档中的一些故事。网红大排档的老板娘、厨师、顾客,他们的邂逅、热爱、留下、离开、和解、团圆,都发生在一段夜色里,发生在充满烟火气的长沙城。 有没有想过这样一个问题…...
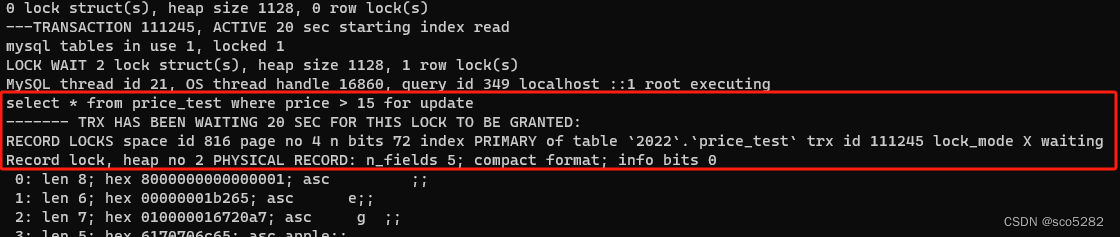
【MYSQL】MYSQL 的学习教程(十一)之 MySQL 不同隔离级别,都使用了哪些锁
聊聊不同隔离级别下,都会使用哪些锁? 1. MySQL 锁机制 对于 MySQL 来说,如果只支持串行访问的话,那么其效率会非常低。因此,为了提高数据库的运行效率,MySQL 需要支持并发访问。而在并发访问的情况下&…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
