经典算法-模拟退火算法的python实现
经典算法-模拟退火算法的python实现
模拟退火算法基本思想
模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却。加温时,固体内部粒子随温度升高变为无序状,内能增大,而缓慢冷却时粒子又逐渐趋有序。从理论上讲,如果冷却过程足够缓慢,那么冷却中任一温度时固体都能达到热平衡,而冷却到低温时将达到这一低温下的内能最小状态。
LLM大模型相关文章:
大模型查询工具助手之股票免费查询接口
GPT实战系列-LangChain + ChatGLM3构建天气查询助手
GPT实战系列-大模型为我所用之借用ChatGLM3构建查询助手
GPT实战系列-简单聊聊LangChain
GPT实战系列-Baichuan2本地化部署实战方案
GPT实战系列-大话LLM大模型训练
GPT实战系列-ChatGLM3本地部署CUDA11+1080Ti+显卡24G实战方案
根据Metropolis准则,粒子在温度T时趋于平衡的概率为e(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变量,k为Boltzmann常数。用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。
因为物理系统总是趋向于能量最低,而分子热运动则趋向于破坏这种低能量的状态,故而只需着重取贡献比较大的状态即可达到比较好的效果, 因而1953年Metropolis提出了这样一个重要性采样的方法, 即设从当前状态i生成新状态j。若新状态的内能小于状态i的内能(即Ej<Ei),则接受新状态j作为新的当前状态; 否则,以概率 e x p [ − ( E j − E i ) K T ] exp[\frac{-(E_j-E_i)}{KT}] exp[KT−(Ej−Ei)]接受状态j, 其中K为Boltzmann常数, 这就是通常所说的Metropolis准则。
初始化算法参数
self.interval = interval # 给定状态空间 - 即待求解空间self.T_max = T_max # 初始退火温度 - 温度上限self.T_min = T_min # 截止退火温度 - 温度下限self.iterMax = iterMax # 定温内部迭代次数self.rate = rate # 退火降温速度
算法基本步骤
①令 T = T 0 T=T_0 T=T0,即开始退火的初始温度,随机生成一个初始解工,并计算相应的目标函数值 E ( x 0 ) E(x_0) E(x0)。
②令T等于冷却进度表中的下一个值 T i T_i Ti。
③根据当前 x i x_i xi,进行扰动(扰动方式可以参考后面的实例),产生一个新解 x j x_j xj、计算应的目标函数值 E ( x j ) E(x_j) E(xj),得到$ △E=E(x_j)一E(x_i)$。
④若△E<0,则新解 x j x_j xj 被接受,作为新的当前解;若 △ E > 0 △E>0 △E>0,则新解 x j x_j xj ,按概率 e x p ( − △ E / T i ) exp(-△E/T_i) exp(−△E/Ti) 接受, T i T_i Ti为当前温度。
⑤在温度 T i T_i Ti下,重复 L k L_k Lk次的扰动和接受过程,即执行步骤③与④。
⑥判断T是否已到达 T j T_j Tj,是,则终止算法;否,则转到步骤②继续执行。
x1 = self.x_seedT = self.T_maxwhile T >= self.T_min:for i in range(self.iterMax):f1 = self.func(x1)delta_x = random.random() * 2 - 1if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内x2 = x1 + delta_xelse:x2 = x1 - delta_xf2 = self.func(x2)delta_f = f2 - f1x1 = deal(x1, x2, delta_f, T)T *= self.rateself.x_solu = x1 # 提取最终退火解
算法实质分两层循环,在任一温度随机扰动产生新解,并计算目标函数值的变化,决定是否被接受。由于算法初始温度比较高,这样,使E增大的新解在初始时也可能被接受。因而能跳出局部极小值,然后通过缓慢地降低温度,算法就最终可能收敛到全局最优解。还有一点要说明的是,虽然在低温时接受函数已经非常小了,但仍不排除有接受更差的解的可能,因此一般都会把退火过程中碰到的最好的可行解(历史最优解)也记录下来,与终止算法前最后一个被接受解一并输出。
参数说明
退火过程由一组初始参数, 即冷却进度表(cooling schedule) 控制, 它的核心是尽量使系统达到准平衡,以使算法在有限的时间内逼近最优解。冷却进度表包括:
- ①控制参数的初值 T 0 T_0 T0:冷却开始的温度。
- ②控制参数T的衰减函数:因计算机能够处理的都是离散数据,因此需要把连续的降温过程离散化成降温过程中的一系列温度点,衰减函数即计算这一系列温度的表达式。
- ③控制参数T的终值 T j T_j Tj,(停止准则)。
- ④Markov链的长度 L k L_k Lk:任一温度T的迭代次数。
参数的选择
(1)控制参数T的初值 T 0 T_0 T0
求解全局优化问题的随机搜索算法一般都采用大范围的粗略搜索,与局部的精细搜索相结合的搜索策略。只有在初始的大范围搜索阶段找到全局最优解所在的区域,才能逐渐缩小搜索的范围.最终求出全局最优解。模拟退火算法是通过控制参数T的初值 T 0 T_0 T0和其衰减变化过程,来实现大范围的粗略搜索和局部精细搜索。
一般来说,只有足够大的 T 0 T_0 T0才能满足算法要求(但对不同的问题“足够大”的含义也不同,有的可能 T 0 T_0 T0=100就可以,有的则要1000)。在问题规模较大时,过小的 T 0 T_0 T0往往导致算法难以跳出局部陷阱而达不到全局最优。但为了减少计算量, T 0 T_0 T0不宜取得过大,而应与其他参数折中选取。
(2)控制参数T的衰减函数
衰减函数可以有多种形式,一个常用的衰减函数是
T k + 1 = α T k , k = 0 , 1 , 2 , . . . T_{k+1} = \alpha T_k, k=0, 1, 2, ... Tk+1=αTk,k=0,1,2,...
其中.a是一个常数,可以取为0.5~0.99,它的取值决定了降温的过程。小的衰减量可能导致算法进程迭代次数的增加,从而使算法进程接受更多的变换,访问更多的邻域,搜索更大范围的解空间,返回更好的最终解。同时由于在 T k T_k Tk值上已经达到准平衡,则在 T k + 1 T_{k+1} Tk+1时只需少量的变换就可达到准平衡。这样就可选取较短长度的Markov链来减少算法时间。
(3) Markov链长度
选取原则:
在控制参数T的衰减函数已选定的前提下, L k L_k Lk 应能使在控制参数T的每一取值上达到准平衡。从经验上来说,对简单的情况可以令 L k L_k Lk =100n,n为问题规模。
算法停止准则:
对Metropolis准则中的接受函数 e x p [ − ( E j − E i ) K T ] exp[\frac{-(E_j-E_i)}{KT}] exp[KT−(Ej−Ei)] 分析可知,在T比较大的高温情况下,指数上的分母比较大,而这是一个负指数,所以整个接受函数可能会趋于1,即比当前解x,更差的新解工,也可能被接受,因此就有可能跳出局部极小而进行广域搜索,去搜索解空间的其他区域;而随着冷却的进行,T减小到一个比较小的值时,接受函数分母小了,整体也小了,即难以接受比当前解更差的解,也就是不太容易跳出当前的区域。如果在高温时,已经进行了充分的广域搜索,找到了可能存在最好解的区域,而在低温再进行足够的局部搜索,则可能最终找到全局最优了。因此,一般T,应设为一个足够小的正数,比如0.01~5,但这只是一个粗糙的经验,更精细的设置及其他的终止准则可以查阅文献。
设计要点
为了更好地实现模拟退火算法,还需要注意以下方面。
状态表达
上文已经提到过,SA算法中优化问题的一个解模拟了(或说可以想象为)退火过程中固体内部的一种粒子分布情况。这里状态表达即指实际问题的解(即状态),如何以一种合适的数学形式被表达出来,它应当适用于SA的求解、又能充分表达实际问题,这需要仔细地设计。
可以参考遗传算法和禁忌搜索中编码的相关内容。常见的表达方式有:背包问题和指派问题的0-1编码, TSP问题和调度问题的自然数编码:还有用于连续函数优化的实数编码等。
新解的产生
新解产生机制的基本要求是能够尽量遍及解空间的各个区域,这样、在某一恒定温度不断产生新解时,就可能跳出当前区域的极小以搜索其他区域,这是模拟退火算法能够进行广域搜索的一个重要条件。
收敛的一般性条件
收敛到全局最优的一般性条件是:
- ①初始温度足够高:
- ②热平衡时间足够长;
- ③终止温度足够低;
- ④降温过程足够缓慢。但上述条件在应用中很难同时满足。
Python实现
函数: f ( x ) = ( x 2 − 5 x ) s i n ( x 2 ) f(x) = (x^2 - 5x)sin(x^2) f(x)=(x2−5x)sin(x2)
import numpy as np
import matplotlib.pyplot as plt
import randomclass SA(object):def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):self.interval = interval # 给定状态空间 - 即待求解空间self.T_max = T_max # 初始退火温度 - 温度上限self.T_min = T_min # 截止退火温度 - 温度下限self.iterMax = iterMax # 定温内部迭代次数self.rate = rate # 退火降温速度#############################################################self.x_seed = random.uniform(interval[0], interval[1]) # 解空间内的种子self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值#############################################################self.solve() # 完成主体的求解过程self.display() # 数据可视化展示def solve(self):temp = 'deal_' + self.tab # 采用反射方法提取对应的函数if hasattr(self, temp):deal = getattr(self, temp)else:exit('>>>tab标签传参有误:"min"|"max"<<<')x1 = self.x_seedT = self.T_maxwhile T >= self.T_min:for i in range(self.iterMax):f1 = self.func(x1)delta_x = random.random() * 2 - 1if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内x2 = x1 + delta_xelse:x2 = x1 - delta_xf2 = self.func(x2)delta_f = f2 - f1x1 = deal(x1, x2, delta_f, T)T *= self.rateself.x_solu = x1 # 提取最终退火解def func(self, x): # 状态产生函数 - 即待求解函数value = np.sin(x**2) * (x**2 - 5*x)return valuedef p_min(self, delta, T): # 计算最小值时,容忍解的状态迁移概率probability = np.exp(-delta/T)return probabilitydef p_max(self, delta, T):probability = np.exp(delta/T) # 计算最大值时,容忍解的状态迁移概率return probabilitydef deal_min(self, x1, x2, delta, T):if delta < 0: # 更优解return x2else: # 容忍解P = self.p_min(delta, T)if P > random.random(): return x2else: return x1def deal_max(self, x1, x2, delta, T):if delta > 0: # 更优解return x2else: # 容忍解P = self.p_max(delta, T)if P > random.random(): return x2else: return x1def display(self):print('seed: {}\nsolution: {}'.format(self.x_seed, self.x_solu))plt.figure(figsize=(6, 4))x = np.linspace(self.interval[0], self.interval[1], 300)y = self.func(x)plt.plot(x, y, 'g-', label='function')plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')plt.plot(self.x_solu, self.func(self.x_solu), 'r*', label='solution')plt.title('solution = {}'.format(self.x_solu))plt.xlabel('x')plt.ylabel('y')plt.legend()plt.savefig('SA.png', dpi=500)plt.show()plt.close()if __name__ == '__main__':SA([-5, 5], 'max')
实际应用中,模拟退火算法的参数和操作可根据具体问题做适当的调整。
觉得有用 收藏 收藏 收藏
点个赞 点个赞 点个赞
End
GPT专栏文章:
GPT实战系列-ChatGLM3本地部署CUDA11+1080Ti+显卡24G实战方案
GPT实战系列-LangChain + ChatGLM3构建天气查询助手
大模型查询工具助手之股票免费查询接口
GPT实战系列-简单聊聊LangChain
GPT实战系列-大模型为我所用之借用ChatGLM3构建查询助手
GPT实战系列-P-Tuning本地化训练ChatGLM2等LLM模型,到底做了什么?(二)
GPT实战系列-P-Tuning本地化训练ChatGLM2等LLM模型,到底做了什么?(一)
GPT实战系列-ChatGLM2模型的微调训练参数解读
GPT实战系列-如何用自己数据微调ChatGLM2模型训练
GPT实战系列-ChatGLM2部署Ubuntu+Cuda11+显存24G实战方案
GPT实战系列-Baichuan2本地化部署实战方案
GPT实战系列-Baichuan2等大模型的计算精度与量化
GPT实战系列-GPT训练的Pretraining,SFT,Reward Modeling,RLHF
GPT实战系列-探究GPT等大模型的文本生成-CSDN博客
相关文章:

经典算法-模拟退火算法的python实现
经典算法-模拟退火算法的python实现 模拟退火算法基本思想 模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却。加温时,固体内部粒子随温度升高变为无序状,内能增大,而缓慢冷却时粒子又逐渐趋有序。…...

谷粒学院项目redirect_uri 参数错误微信二维码登录
谷粒学院项目redirect_uri 参数错误_redirect_uri": "http%3a%2f%2fguli.shop%2fapi%2fuce-CSDN博客 修改本地配置 # ����˿� server.port8160 # ����&#x…...
Jenkins+nexus
jiekins安装完成 1、安装java环境 [rootnexus ~]# tar -xf jdk-8u211-linux-x64.tar.gz -C /usr/local [rootnexus ~]# vim /etc/profile.d/java.sh JAVA_HOME/usr/local/jdk1.8.0_211 PATH$PATH:$JAVA_HOME/bin [rootnexus ~]# source /etc/profile.d/java.sh 必须要选择与n…...
「JavaSE」类和对象1
🎇个人主页:Ice_Sugar_7 🎇所属专栏:快来卷Java啦 🎇欢迎点赞收藏加关注哦! 类和对象 🍉类的定义🍌类的实例化 🍉this引用🍉对象的构造及初始化🍌…...
Ubuntu server搭建dhcp服务器
安装 直接使用一下命令进行安装 apt-get install isc-dhcp-server 以下就是安装好的图片 然后进入dhcp目录 cd /etc/dhcp 进入后用ls查看当前目录存在哪些文件 使用如下进入dhcp.conf vim dhcpd.conf 红:设置ip域和子网掩码 绿:设置ip池范围 黄…...
2024--Django平台开发-Web框架和Django基础(二)---Mysql多版本共存(Mac系统)
MySQL多版本共存(Mac系统) 想要在Mac系统上同时安装【MySQL5.7 】【MySQL8.0】版本,需要进行如下的操作和配置。 想要同时安装两个版本可以采取如下方案: 方案1:【讲解】 MySQL57,用安装包进行安装。 MyS…...

Pytorch 反向传播 计算图被修改的报错
先看看报错的内容 RuntimeError: one of the variables needed for gradient computation has been modified by an inplace operation: [torch.FloatTensor [5, 1]], which is output 0 of AsStridedBackward0, is at version 2; expected version 1 instead. Hint: enable an…...
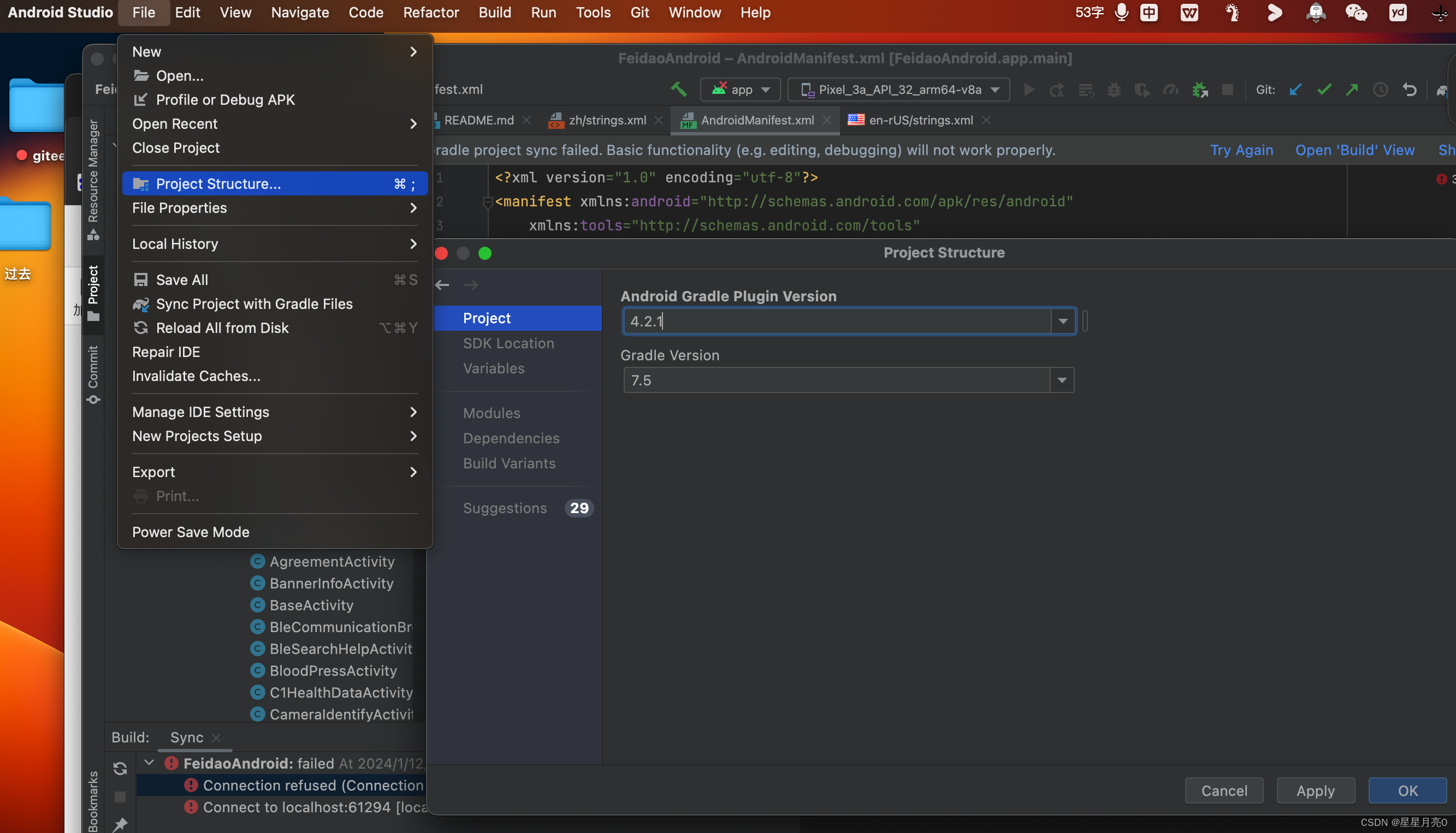
android studio设置gradle和gradle JDK版本
文章目录 1.gradle JDK版本2.gradle版本 1.gradle JDK版本 file -> project structure -> SDK Location -> Gradle Settings -> Gradle JDK -> Download JDK 2.gradle版本 file -> project structure -> Project...
Android 15即将到来,或将推出5大新功能特性
Android15 OneUI电池优化 三星最近完成了对其所有设备的稳定版 One UI 6.0 更新的推出,引起了用户的极大兴奋。据新出现的互联网统计数据显示,即将发布的基于 Android 15 的 One UI 7 将通过优化电池和功耗来重新定义用户体验,这是一项具有突…...
)
sqlalchemy 事务自动控制(类java aop)
最近使用它交互数据库,想实现类似java aop那种自动事务控制,不用手动commit或者rollback。我是用的是flaskdenpendency-injecter 这是我的db的配置类,里面会初始化一些session配置,里面比较重要的是把autocommit和autoflush关闭了…...

vue2-手写轮播图
轮播图5长展示,点击指示器向右移动一个图片,每隔2秒移动一张照片! <template><div class"top-app"><div class"carousel-container"><div class"carousel" ref"carousel">&…...

Google I/O大会:Android 13
3个体验升级的方向 以智能手机为场景核心、 扩大智能终端的应用边界以及实现多设备间更好地协同。具体到系统体验层,安卓13将支持图标颜色随主题更换、为不同应用设定使用的语言、新的媒体中心界面等等,同时谷歌也推出了自家的钱包应用(Goog…...

VUE指令(一)
vue会根据不同的指令,针对不同的标签实现不同的功能。指令是带有 v- 前缀的特殊标签属性。指令的职责是,当表达式的值改变时,将其产生的连带影响,响应式地作用于 DOM。 1、v-text:设置元素的文本内容,不会解…...
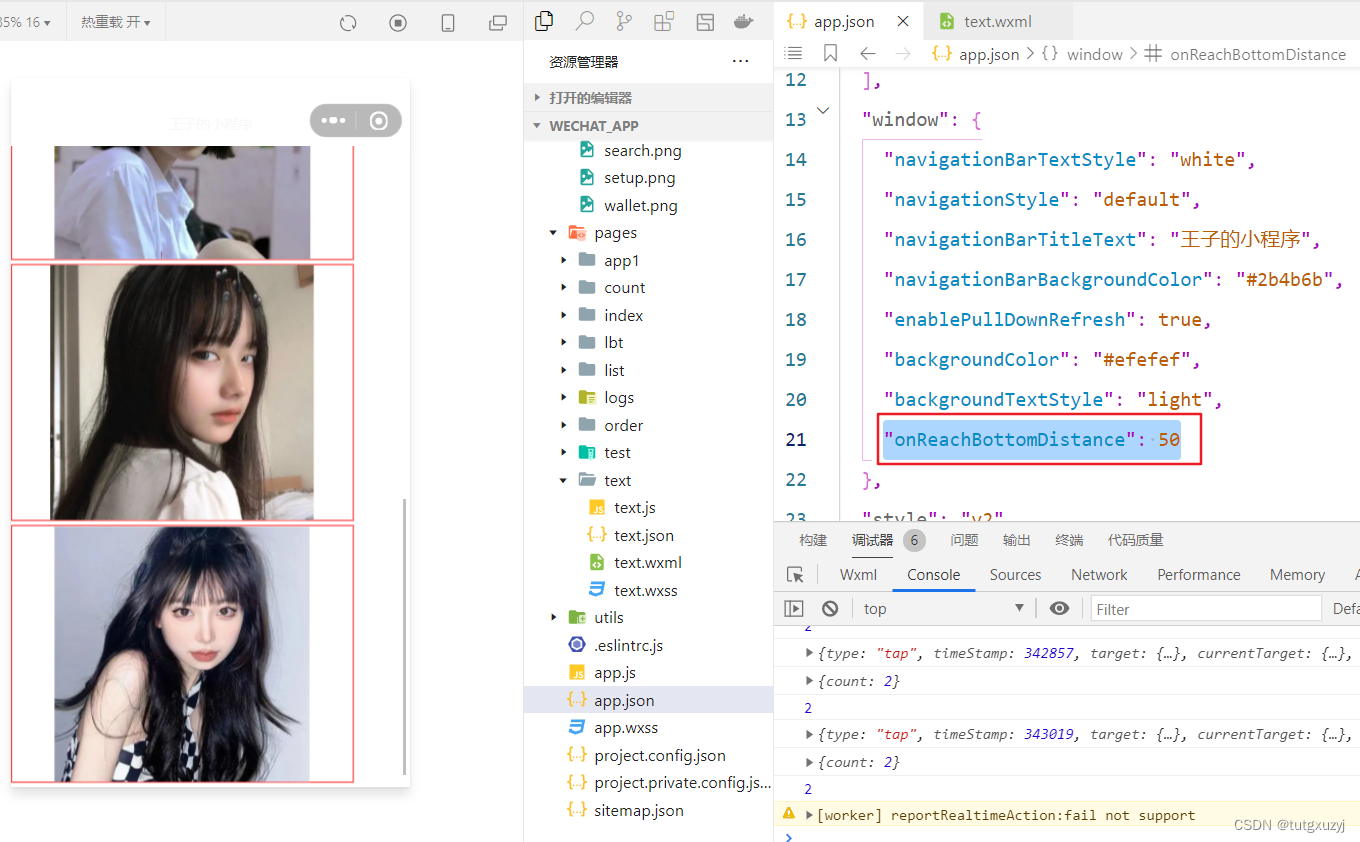
微信小程序开发学习笔记《7》全局配置以及小程序窗口
微信小程序开发学习笔记《7》全局配置以及小程序窗口 博主正在学习微信小程序开发,希望记录自己学习过程同时与广大网友共同学习讨论。全局配置官方文档 一、全局配置文件及常用的配置项 小程序根目录下的app.json 文件是小程序的全局配置文件。 常用的配置项如…...
Vue、uniApp、微信小程序、Html5等实现数缓存
此文章带你实现前端缓存,利用时间戳封装一个类似于Redis可以添加过期时间的缓存工具 不仅可以实现对缓存数据设置过期时间,还可以自定义是否需要对缓存数据进行加密处理 工具介绍说明 对缓存数据进行非对称加密处理 对必要数据进行缓存,并…...
如何将ArcGIS工程文件迁移到ArcGIS Pro内
当你刚接触ArcGIS Pro的时候,尝试新建一个工程文件会发现工程文件的后缀已经改变,那么以前在ArcGIS内辛苦制作的工程文件是否就不能在ArcGIS Pro内使用了,答案是否定的,对此Esri也给出了解决方案,这里为大家介绍一下迁…...

Jenkins基础篇--添加用户和用户权限设置
添加用户 点击系统管理,点击管理用户,然后点击创建用户(Create User) 用户权限管理 点击系统管理,点击全局安全配置,找到授权策略,选择安全矩阵,配置好用户权限后,点击…...

C语言基础内容(七)——第08章_C语言常用函数
文章目录 第08章_C语言常用函数本章专题脉络1、字符串相关函数1.1 字符串的表示方式1.2 两种方式的区别1.2 字符串常用函数strlen()strcpy()strncpy()strcat()strncat()strcmp()strlwr()/strupr()1.3 基本数据类型和字符串的转换基本数据类型 -> 字符串字符串 -> 基本数据…...

CRM系统针对销售管理有哪些功能?如何帮助销售效率增长?
从长远来看,有效的CRM管理系统可以帮助您的企业达到甚至超过收入目标。现代大多数企业都依靠CRM系统来管理其销售周期并增加收入。但是,当大多数人提到CRM时,他们指的是使能够改善业务关系并轻松管理不断团队的软件或工具。合格的CRM系统能够…...

基于Pixhawk和ROS搭建自主无人车(一):底盘控制篇
参考 ArduPilot Development超维空间科技乐迪MiniPix车船使用说明书 1. 硬件篇 1.1 底盘构成一览 1.2 底盘接线示意 2. 软件篇 2.1 APM 固件下载 pixhawk 是硬件平台,PX4 是 pixhawk 的原生固件,APM(Ardupilot Mega)是硬件平台…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
