Open CASCADE学习|参数化球面的奇异性
参数曲面的奇异性是一个相对复杂的概念,它涉及到参数曲面的几何特性和参数化过程中的一些特殊情况。参数曲面通常用于描述三维空间中的复杂形状,通过参数方程将二维参数域映射到三维空间中。然而,在某些情况下,参数曲面可能会表现出奇异性,即参数映射不再是一对一的或者曲面上的某些点无法正常表示。
参数曲面的奇异性可以分为几种类型,包括但不限于以下几种情况:
自交点:参数曲面上的不同参数可能对应到三维空间中的同一个点,导致曲面在自交点处不再是单射的。这种情况下,参数化失去了唯一性,自交点附近的区域可能会产生几何上的扭曲或变形。
折叠或褶皱:参数曲面在某些区域可能会发生折叠或褶皱现象,即曲面上的相邻点被映射到三维空间中的远离位置。这种情况下,曲面的法向量可能会突然改变方向,导致几何上的不连续性和可视化上的问题。
奇异点或奇异曲线:参数曲面上可能存在一些特殊的点或曲线,称为奇异点或奇异曲线。在这些位置,曲面的几何属性(如法向量、曲率等)可能会变得无限大或无法定义,导致曲面在这些位置失去光滑性。
奇异性对于参数曲面的应用和分析具有重要影响。在几何建模、计算机图形学和物理模拟等领域,奇异性的存在可能导致计算错误、渲染问题或模拟失真。因此,在设计和处理参数曲面时,需要特别关注奇异性的检测和避免,以确保曲面的几何正确性和应用的可靠性。
为了避免奇异性,可以采取一些策略,如选择合适的参数化方法、优化参数化过程、使用适当的约束条件等。此外,对于已经存在奇异性的参数曲面,可以尝试进行修复或平滑处理,以恢复曲面的几何连续性和光滑性。
在OpenCascade中球面的参数方程为:
![]()
分别沿u,v方向求偏导矢,即分别沿经线和纬线的速度矢量,得:
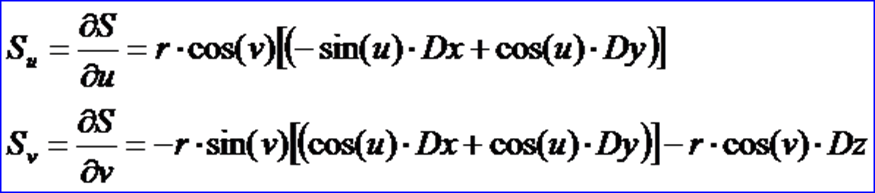
曲面在一点处存在法矢及相应切平面是曲面的几何性质,与曲面的参数化无关。因此,尽管不同的参数化会产生不同的偏导矢,但只要u或v方向上的切矢都不为零,则将u,v的切矢叉乘单位化后的法向是都是相同的。OpenCascade中的球面,对于所有的u∈[0, 2π]有:

即Su在球面的北极和南极消失(为零矢量),对应v=-π/2和v=π/2时的两个边就分别退化(Degenerated)成两个点。很明显,球面在两个极点的法矢确实是存在的,但在这种参数化之下,无法用上述方法来计算它的法向量。
#define WNT
#include <TopoDS.hxx>
#include <TopExp.hxx>
#include <TopExp_Explorer.hxx>
#include <BRepPrimAPI_MakeSphere.hxx>
#include <TopTools_ListIteratorOfListOfShape.hxx>
#include <TopTools_IndexedDataMapOfShapeListOfShape.hxx>
/**
* @breif Find the face for the given edge, i.e the face which the given edge is on it.
*/
TopoDS_Face FindFaceOfEdge(const TopoDS_Shape& theShape, const TopoDS_Edge& theEdge)
{TopoDS_Face theFace;
TopTools_IndexedDataMapOfShapeListOfShape theMap;TopExp::MapShapesAndAncestors(theShape, TopAbs_EDGE, TopAbs_FACE, theMap);
const TopTools_ListOfShape& theFaces = theMap.FindFromKey(theEdge);TopTools_ListIteratorOfListOfShape theIterator(theFaces);
for (theIterator.Initialize(theFaces); theIterator.More(); theIterator.Next()){theFace = TopoDS::Face(theIterator.Value());}return theFace;
}
void TestSingularity(void)
{TopoDS_Shape theSphere = BRepPrimAPI_MakeSphere(1.0);
for (TopExp_Explorer edgeExp(theSphere, TopAbs_EDGE); edgeExp.More(); edgeExp.Next()){const TopoDS_Edge anEdge = TopoDS::Edge(edgeExp.Current());
Standard_Real aFirst = 0.0;Standard_Real aLast = 0.0;
gp_Pnt2d U1V1;gp_Pnt2d U2V2;
Standard_Boolean IsDegenerated = BRep_Tool::Degenerated(anEdge);
BRep_Tool::Range(anEdge, aFirst, aLast);BRep_Tool::UVPoints(anEdge, FindFaceOfEdge(theSphere, anEdge), U1V1, U2V2);
std::cout << "Edge is Degenerated: " << (IsDegenerated ? "True" : "False") << std::endl;std::cout << "Edge parameters on face: " << std::endl;std::cout << " (" << U1V1.X() << ", " << U1V1.Y() << ")" << std::endl;std::cout << " (" << U2V2.X() << ", " << U2V2.Y() << ")" << std::endl;std::cout << std::endl;}
}
int main(int argc, char* argv[])
{TestSingularity();return 0;
}
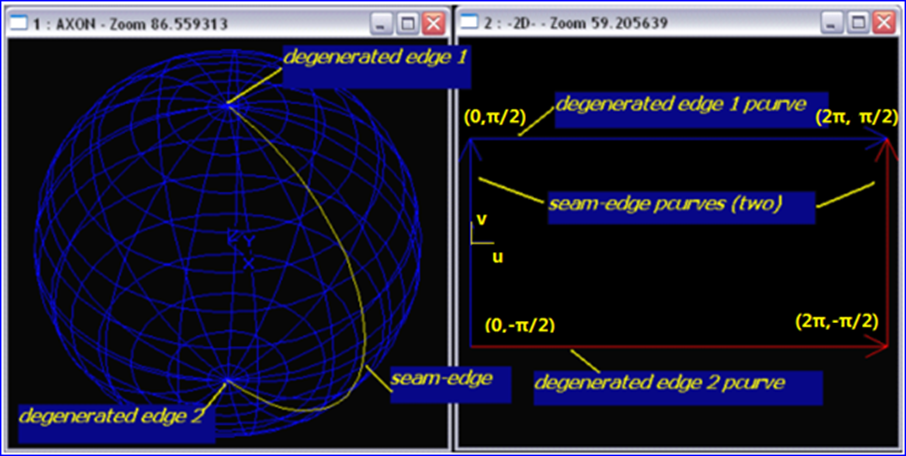
Edge is Degenerated: True
Edge parameters on face:
(0, 1.5708)
(6.28319, 1.5708)
Edge is Degenerated: False
Edge parameters on face:
(6.28319, -1.5708)
(6.28319, 1.5708)
Edge is Degenerated: True
Edge parameters on face:
(0, -1.5708)
(6.28319, -1.5708)
Edge is Degenerated: False
Edge parameters on face:
(0, -1.5708)
(0, 1.5708)
相关文章:

Open CASCADE学习|参数化球面的奇异性
参数曲面的奇异性是一个相对复杂的概念,它涉及到参数曲面的几何特性和参数化过程中的一些特殊情况。参数曲面通常用于描述三维空间中的复杂形状,通过参数方程将二维参数域映射到三维空间中。然而,在某些情况下,参数曲面可能会表现…...
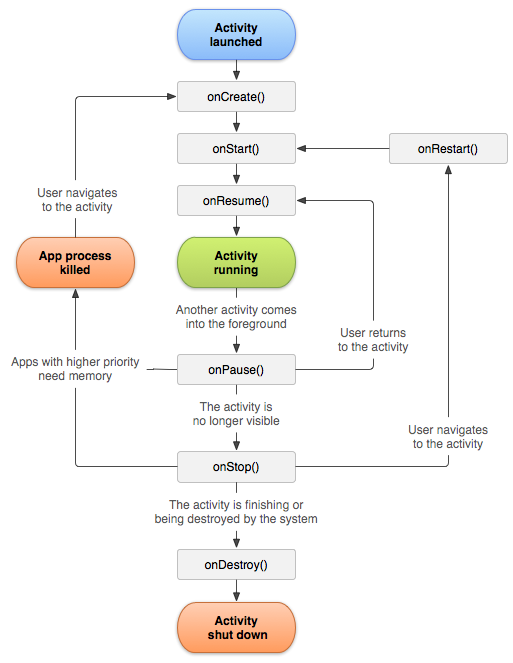
基础知识篇(一)Acticity生命周期
Activity 类是 Android 应用的关键组件,而 activity 的启动和组合方式是平台应用模型的基本组成部分。与使用 main() 方法启动应用的编程范式不同,Android 系统会通过调用与其生命周期特定阶段对应的特定回调方法,在 Activity 实例中启动代码…...

Java内存结构
前文: 《Java8之类的加载》 《Java8之类加载机制class源码分析》 写在开头:本文为学习后的总结,可能有不到位的地方,错误的地方,欢迎各位指正。 JVM 在执行 Java 程序的过程中会把它所管理的内存划分为若干个不同的数…...
Java--ListUtil工具类,实现将一个大列表,拆分成指定长度的子列表
文章目录 前言实现代码执行结果 前言 在项目中有时会出现列表很大,无法一次性批量操作,我们需要将列表分成指定大小的几个子列表,一份一份进行操作,本文提供这样的工具类实现这个需求。 实现代码 以下为ListUtil工具类代码实现…...

SpringSecurity 密码加密登录
SpringSecurity 密码加密登录 1.前端所需文件2.后端所用工具类3.登录代码4.灵魂一问 1.前端所需文件 import JSEncrypt from jsencrypt/bin/jsencrypt.min// 密钥对生成 http://web.chacuo.net/netrsakeypairconst publicKey MFwwDQYJKoZIhvcNAQEBBQADSwAwSAJBAKoR8mX0rGKLqz…...
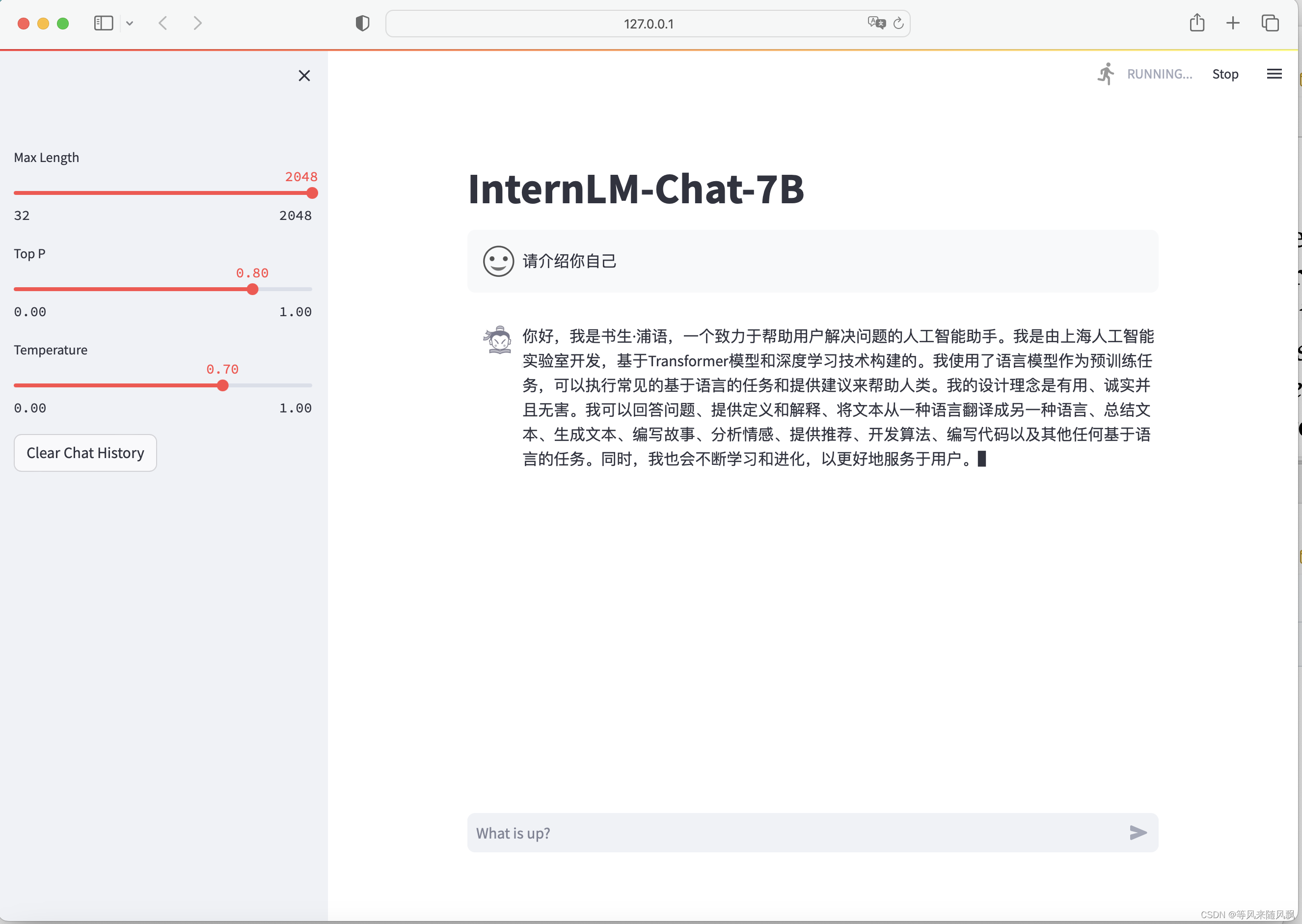
大模型实战作业03
大模型实战作业03 注: 因为微调数据较少,没有显示出个人助手的名字...

【AI视野·今日Sound 声学论文速览 第四十四期】Tue, 9 Jan 2024
AI视野今日CS.Sound 声学论文速览 Tue, 9 Jan 2024 Totally 27 papers 👉上期速览✈更多精彩请移步主页 Daily Sound Papers DJCM: A Deep Joint Cascade Model for Singing Voice Separation and Vocal Pitch Estimation Authors Haojie Wei, Xueke Cao, Wenbo Xu…...

Windows Copilot 更新及使用教程
Windows Copilot 是一款由微软开发的人工智能辅助工具,可以通过学习用户的操作习惯和上下文,自动完成代码编写和其他重复性任务。它可以帮助开发人员提高工作效率,减少重复劳动。 以下是关于Windows Copilot的更新和使用教程的一些信息&…...

【Android开发】不同Activity之间的数据回传实例(一)摘桃子游戏
一、功能介绍 该项目实现的功能主要有: 在首页显示一个按钮点击该按钮跳转到桃园页面在桃园页面,点击桃子会弹窗显示摘到几个桃子,同时被点击桃子消失,总桃子数1点击退出桃园会返回首页,首页桃子数会根据点击的桃子数…...
增量式PID和脉冲轴组合控制阀门开度(算法介绍)
这篇博客我们以S7-1200PLC平台来举例,介绍我们的PID闭环控制器如何控制脉冲轴实现阀门角度控制。SMART PLC PID控制器控制伺服驱动器实现关节角度控制详细内容请参考下面文章: https://rxxw-control.blog.csdn.net/article/details/129658364https://rxxw-control.blog.csdn…...

解决Vue.js Devtools未检测到Vue实例的问题
解决Vue.js Devtools未检测到Vue实例的问题 解决Vue.js Devtools未检测到Vue实例的问题1. 确保Vue.js已正确加载1.1 在HTML文件中直接引入1.2 在构建工具(如Webpack)中配置引入1.3 检查与验证 2. 检查Vue.js Devtools扩展安装状态2.1 打开Chrome浏览器扩…...

【Java基础】进程与线程,并发与并行,CPU单核与多核
目录 1 进程与线程2 CPU单核与多核 1 进程与线程 进程与线程基本单位的对象不同 进程是操作系统进行资源分配(包括cpu、内存、磁盘IO等)的最小单位线程是CPU调度和分配的基本单位 CPU看不到进程,只能看到待分配的一些线程 并发与并行 并发&…...
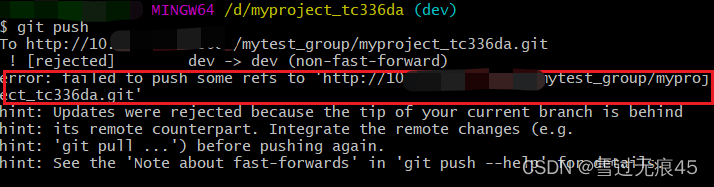
git修改最新提交(commit)信息
一、修改最近一次commit信息 1、首先通过git log查看commit信息 2、使用命令git commit --amend进入命令命令模式,按i进入编辑模式,修改好commit信息后按Esc键退出编辑模式,然后输入:wq保存编辑信息(注意使用英文输入法…...
想寻找Axure的替代品?我们已经试用了10+款设计工具,来看看吧!
Axure是许多产品经理和设计师进入快速原型设计的首选工具,但Axure的使用成本相对较高,学习曲线陡峭,许多设计师正在寻找可以取代Axure的原型设计工具,虽然现在有很多可选的设计工具,但质量不均匀,可以取代A…...
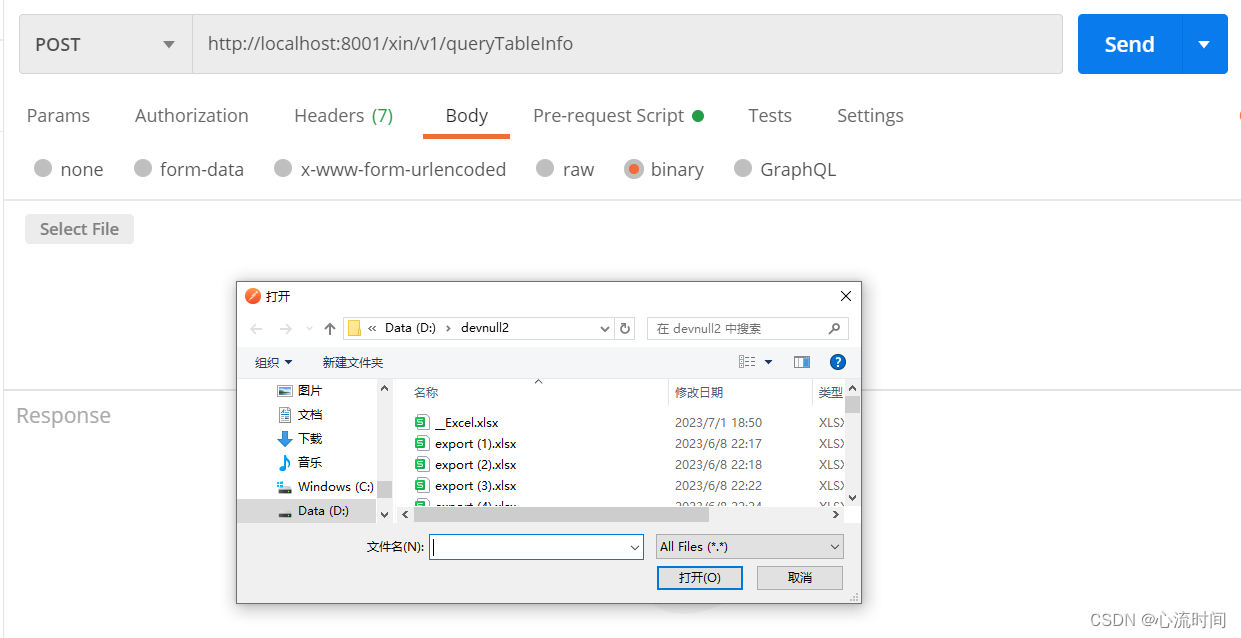
报文大小限制、请求体类型总结
文章目录 1. 各节点请求体有无限制1.1 http协议1.2 TCP/IP层限制1.3 浏览器1.4 nginx1.5 gateway1.6 tomcat1.7 springboot1.8 内存、磁盘处理不了一切白搭 2. 请求体类型2.1 application/x-www-form-urlencoded2.2 multipart/form-data2.3 application/json2.4 text/plain2.5 …...

rknn加载onnx时报错 GLIBC=2.29 no found librknnc.so
rknn 中onnx转rknn在虚拟机中运行时发现报错. GLIBC2.29 no found /****/librknnc.so 昨天还正常的, 今天装了个ftp 和宝塔面板就出错了. 我估计根据报错地址, 找到了librknnc.so文件, 权限也给了777仍然不行 , 我怀疑是GLIBC的版本不对 ,网上给的方法是下载源码, 然后自己手动…...
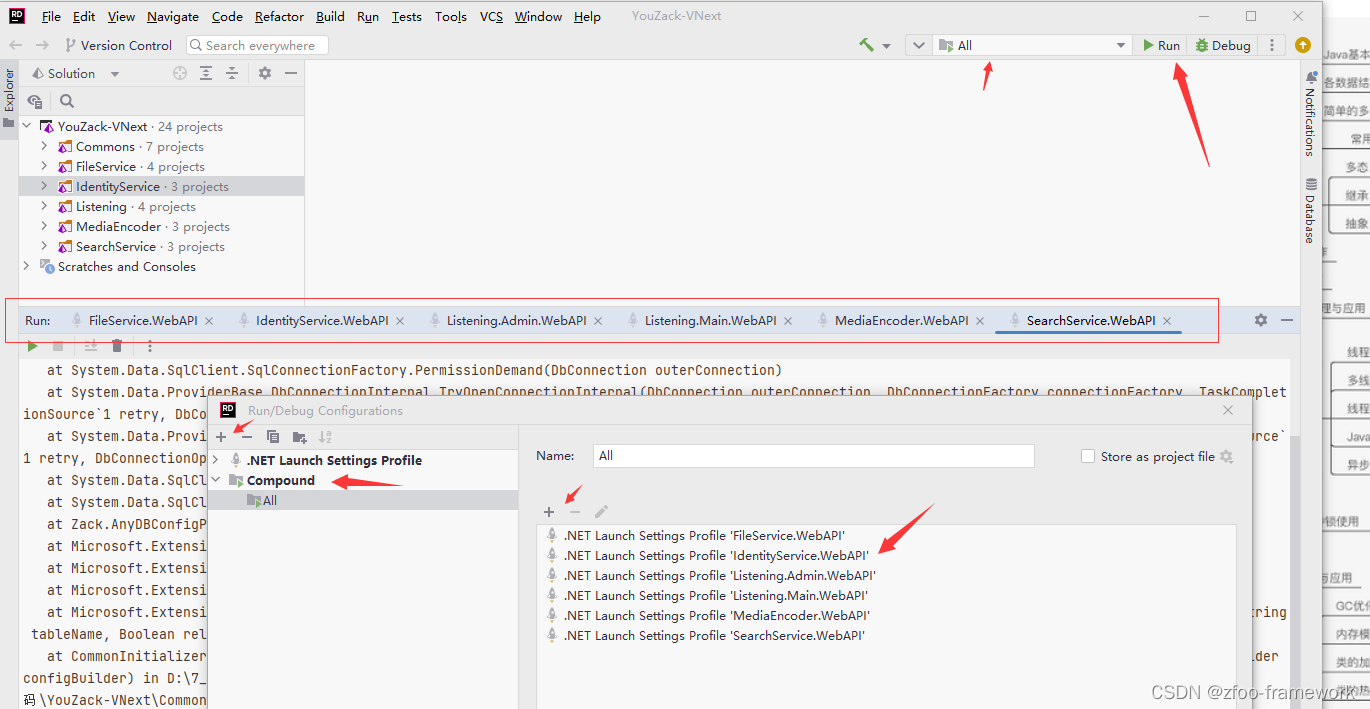
ASP .net core微服务实战(杨中科)
背景: 主要是思考下,我们为什么要用微服务? 微服务我现在理解是:提供了我们一种模块化的手段,一个服务负责一种类型的业务,是一种面对复杂问题进行拆分的方式,但是也会引入一些中间件…...

使用命令行方式搭建uni-app + Vue3 + Typescript + Pinia + Vite + Tailwind CSS + uv-ui开发脚手架
使用命令行方式搭建uni-app Vue3 Typescript Pinia Vite Tailwind CSS uv-ui开发脚手架 项目代码以上传至码云,项目地址:https://gitee.com/breezefaith/uniapp-vue3-ts-scaffold 文章目录 使用命令行方式搭建uni-app Vue3 Typescript Pinia V…...
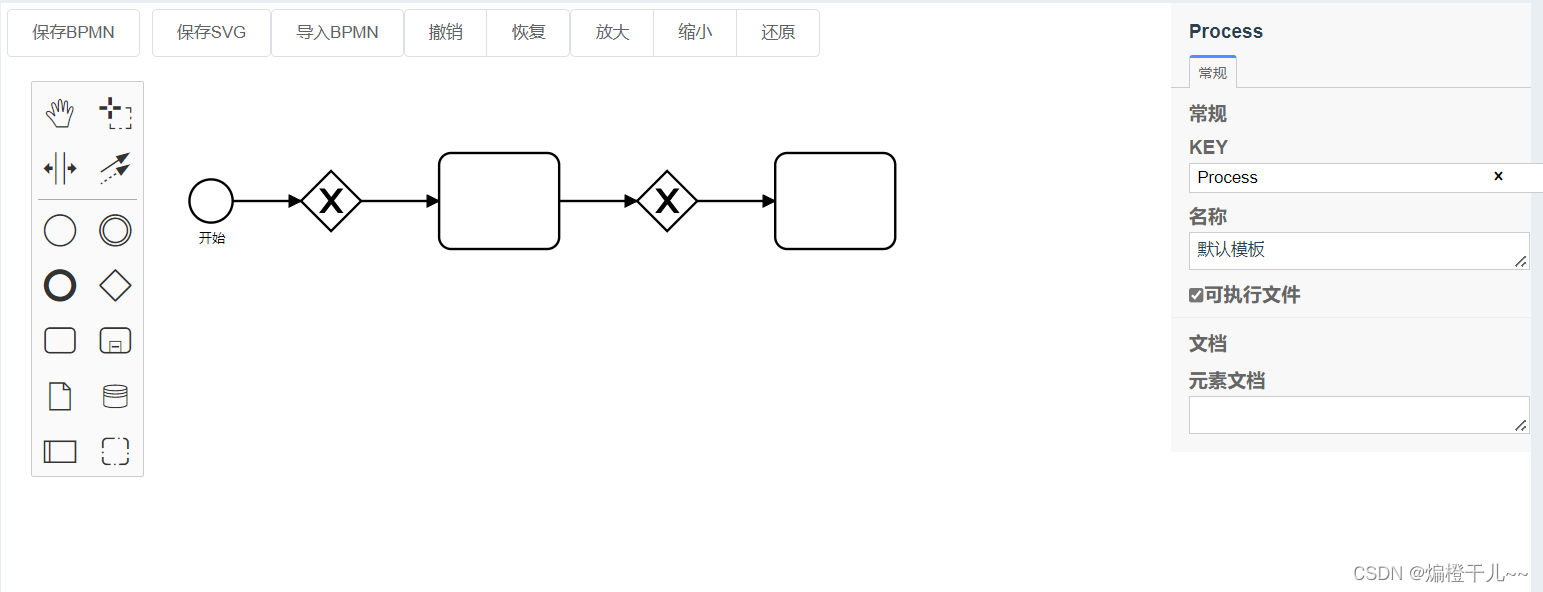
VUE+bpmn.js实现工作流
1、安装bpmn.js npm install bpmn-js7.3.1 // 我安装的版本是7.3.1npm install bpmn-js-properties-panel0.37.2npm install bpmn-moddle7.1.3 npm install --save camunda-bpmn-moddle 2、配置axios,在main.js中引入axios import axios from axiosVue.proto…...

微信小程序Burp抓包
方法有很多,工具也各有差异,主要是学代理流量的思路 Burp流量代理工具小程序 一、Burp证书导入 1、开启代理 开启浏览器的代理,火狐推荐FoxyProxy,Google推荐SwitchyOmega,设置代理为127.0.0.1:8080。 2、下载证书…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
