逆矩阵计算
目录
一、逆矩阵的定义
核心:AB = BA = E
1)定义
2)注意
3)逆矩阵存在的条件|A| != 0
二、核心公式:
三、求逆矩阵(核心考点)
1、伴随矩阵法
2、初等变换法(重点掌握!!)
3、如何理解?
4、什么是初等矩阵?
5、三个基本的初等变换
一、逆矩阵的定义
核心:AB = BA = E
1)定义
A、B为同阶矩阵,如果存在AB = BA = E,即称B为A的逆矩阵,同理,A也是B的逆矩阵。
记作
2)注意
1)不是所有的矩阵都存在逆矩阵
2)只有方阵才存在逆矩阵
3)如果逆矩阵存在,逆矩阵唯一
3)逆矩阵存在的条件|A| != 0
二、核心公式:
三、求逆矩阵(核心考点)
1、伴随矩阵法
这个方法很操蛋,但凡正常理智的人都不会这样去算,因为这是根据公式来计算的,需要计算出|A|和伴随
,计算量可想而知,因此事实上伴随阵就是属于所谓鸡肋,食之无味,弃之可惜。
2、初等变换法(重点掌握!!)
例题:求A的逆矩阵?
1)写出(A,E)

2)利用初等变换,行列均可,将A化成单位阵;同时,右边的单位阵E也进行与A相同的初等变换。通俗来说,就是A怎么变,E也怎么变。举个例子,A中的第1行和第3行交换,E也第1行和第3行交换。最后,当A化为单位阵,E就是。

3、如何理解?
其实非常简单,对于两个矩阵(A,E),
将带进去后:(A
,E
),
你会发现:
A = E
E =
这个括号内的东西,就是我们要求的逆矩阵。
为什么可以这样呢?
因为我们做的一系列的变换,
事实上,本质上,就是对A和E都乘以一个,对不对?
而,要理解这个计算的关键点在于:一个可逆矩阵可以写成一系列初等矩阵的乘积
所以,事实上,我们是将化成了一系列的初等矩阵。
4、什么是初等矩阵?
对单位阵进行一次初等变换所得到的矩阵叫做初等矩阵。
5、三个基本的初等变换
1、某两行(列)交换位置
2、某一行(列)乘某一个数
3、某一行(列)乘以某一个数加到另一行(列)
注意:A左乘一个初等矩阵,相当于对A做相应的初等行变换
A右乘一个初等矩阵,相当于对A做相应的初等列变换
相关文章:
逆矩阵计算
目录 一、逆矩阵的定义 核心:AB BA E 1)定义 2)注意 3)逆矩阵存在的条件|A| ! 0 二、核心公式: 三、求逆矩阵(核心考点) 1、伴随矩阵法 2、初等变换法(重点掌握ÿ…...

《豫鄂烽火燎原大小焕岭》:一部穿越时空的历史史诗
《豫鄂烽火燎原大小焕岭》:一部穿越时空的历史史诗 一部赓续红色血脉的生动教材 一部讴歌时代英雄和人民精神宝典 当历史的烽烟渐渐远去,留下的是一页页泛黄的记忆和无数英雄的壮丽诗篇。李传铭的力作《豫鄂烽火燎原大小焕岭》正是这样一部深情的回望&am…...

浅研究下 DHCP 和 chrony
服务程序: 1.如果有默认配置,请先备份,再进行修改 2.修改完配置文件,请重启服务或重新加载配置文件,否则不生效 有些软件,安装包的名字和系统里服务程序的名字不一样(安装包名字:…...
【算法】动态中位数(对顶堆)
题目 依次读入一个整数序列,每当已经读入的整数个数为奇数时,输出已读入的整数构成的序列的中位数。 输入格式 第一行输入一个整数 P,代表后面数据集的个数,接下来若干行输入各个数据集。 每个数据集的第一行首先输入一个代表…...

mysql服务多实例运行
1、官网下载mysql安装包 https://downloads.mysql.com/archives/community/ 2、解压安装包 tar -zxvf mysql-8.1.0-linux-glibc2.28-aarch64.tar.xz -C /usr/localmv /usr/local/mysql-8.1.0-linux-glibc2.28-aarch64 /usr/local/mysql 3、创建mysql用户组 groupadd…...

「HDLBits题解」Module fadd
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 题目链接:Module fadd - HDLBits module top_module (input [31:0] a,input [31:0] b,output [31:0] sum );//wire [15:0] t1, t2 ; wire co…...
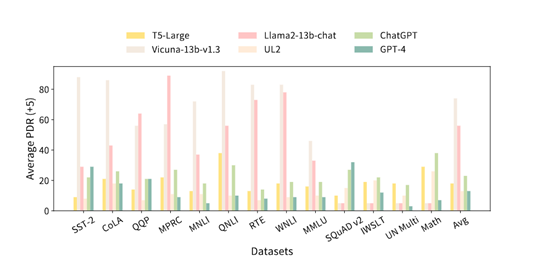
微软等开源评估ChatGPT、Phi、Llma等,统一测试平台
微软亚洲研究院、中国科学院自动化研究所、中国科学技术大学和卡内基梅隆大学联合开源了,用于评估、分析大语言模型的统一测试平台——PromptBench。 Prompt Bench支持目前主流的开源、闭源大语言模型,例如,ChatGPT、GPT-4、Phi、Llma1/2、G…...
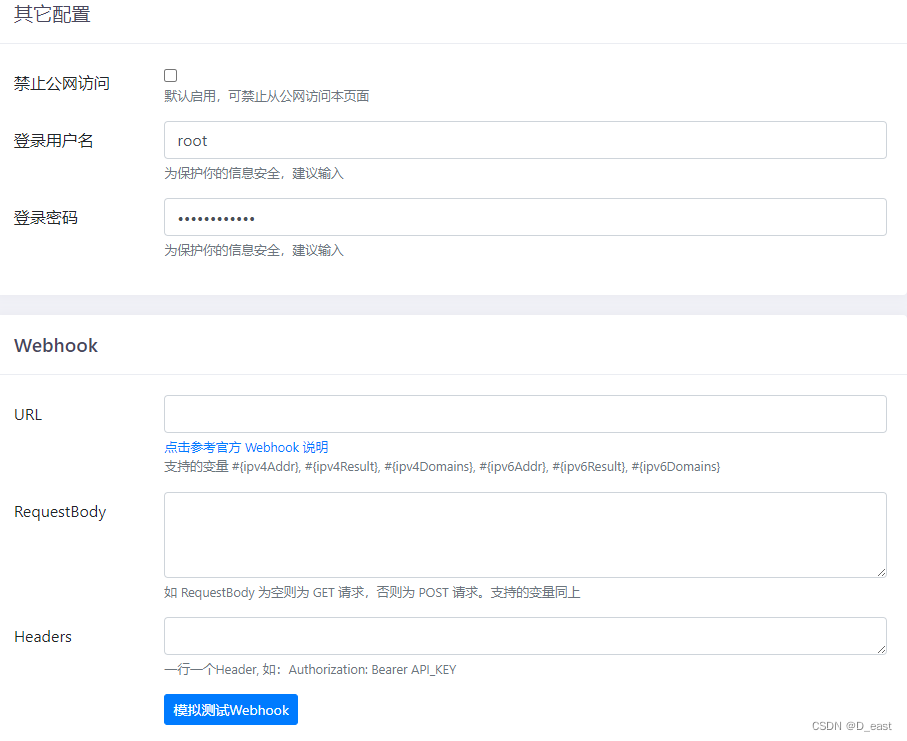
DDNS-GO配置使用教程
环境:openwrt 下载地址:Releases jeessy2/ddns-go GitHub 下载 ssh至openwrt根目录,根据你的处理器选择要下载的版本,我是路由器,选择的是 ddns-go_5.7.1_linux_arm64.tar.gz wget github链接 安装 tar -zxvf…...

flex弹性盒子常用的布局属性详解
想必大家在开发中经常会用到flex布局。而且还会经常用到 justify-content 属性实现分栏等等 接下来给大家分别讲一下 justify-content 的属性值。 以下是我敲的效果图大家可以清晰看出区别 space-between 属性值可以就是说两端对齐 space-evenly 属性值是每个盒子之间的…...
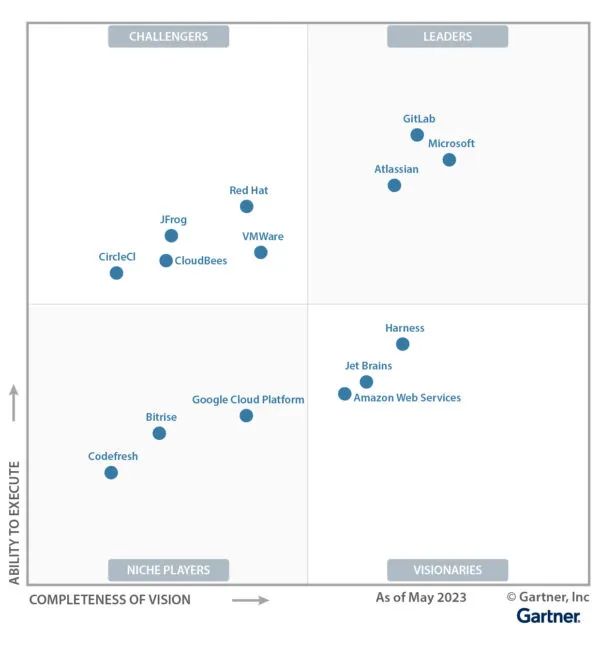
2023年Gartner® DevOps平台魔力象限发布,Atlassian被评为“领导者”
Atlassian在2023年Gartner魔力象限的DevOps平台评选中,被评为领导者。 Gartner根据执行能力和愿景的完整性,对全球14家DevOps平台提供商进行了评估,并发布2023年Gartner魔力象限。其中,Atlassian被评为领导者。 Atlassian提供了一…...
kylin集群使用nginx反向代理
前文已经提到,我安装了kylin集群。 kylin3集群问题和思考(单机转集群)-CSDN博客文章浏览阅读151次,点赞3次,收藏6次。由于是同一个集群的,元数据没有变化,所以,直接将原本的kylin使用…...
小红书搜索团队提出全新框架:验证负样本对大模型蒸馏的价值
大语言模型(LLMs)在各种推理任务上表现优异,但其黑盒属性和庞大参数量阻碍了它在实践中的广泛应用。特别是在处理复杂的数学问题时,LLMs 有时会产生错误的推理链。传统研究方法仅从正样本中迁移知识,而忽略了那些带有错…...

汽车销售领域相关专业术语
引言 本文是笔者在从事汽车销售领域信息化建设过程,积累的一些专业术语注解,供诸位参考交流。 专业术语清单 4S店 汽车销售服务4S店;是由经销商投资建设,按照汽车生产厂家规定的标准建造,是一种集整车销售(Sale)、零配件(Sparepart)、售后服务(Service)、信息…...

代币合约 ERC20 Token接口
代币合约 在以太坊上发布代币就要遵守以太坊的规则,那么以太坊有什么规则呢?以太坊的精髓就是利用代码规定如何运作,由于在以太坊上发布智能合约是不能修改和删除的,所以智能合约一旦发布,就意味着永久有效,不可篡改…...

判断回文字符串—C语言
题目要求 输入一个字符串,判断该字符串是否为回文。回文就是字符串中心对称,从左向右读和从右向左读的内容是一样的。 输入格式: 输入在一行中给出一个不超过80个字符长度的、以回车结束的非空字符串。 输出格式: 输出在第1行中…...
如何在Docker本地搭建流程图绘制神器draw.io并实现公网远程访问
推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站 前言 提到流程图,大家第一时间可能会想到Visio,不可否认,VIsio确实是功能强大,但是软…...

Web前端篇——el-timeline+el-scrollbar时间轴数据刷新后自动显示滚动条
背景:使用el-timelineel-scrollbar显示时间轴,当时间轴数据刷新时,el-scrollbar滚动条会自动隐藏。 当给el-scrollbar设置了永久显示滚动条(如下代码),以为可以一劳永逸,发现问题仍然存在。 .…...

Flutter 监听前台和后台切换的状态
一 前后台的切换状态监听 混入 WidgetsBindingObserver 这个类,这里提供提供了程序状态的一些监听 二 添加监听和销毁监听 overridevoid initState() {super.initState();//2.页面初始化的时候,添加一个状态的监听者WidgetsBinding.instance.addObserver…...
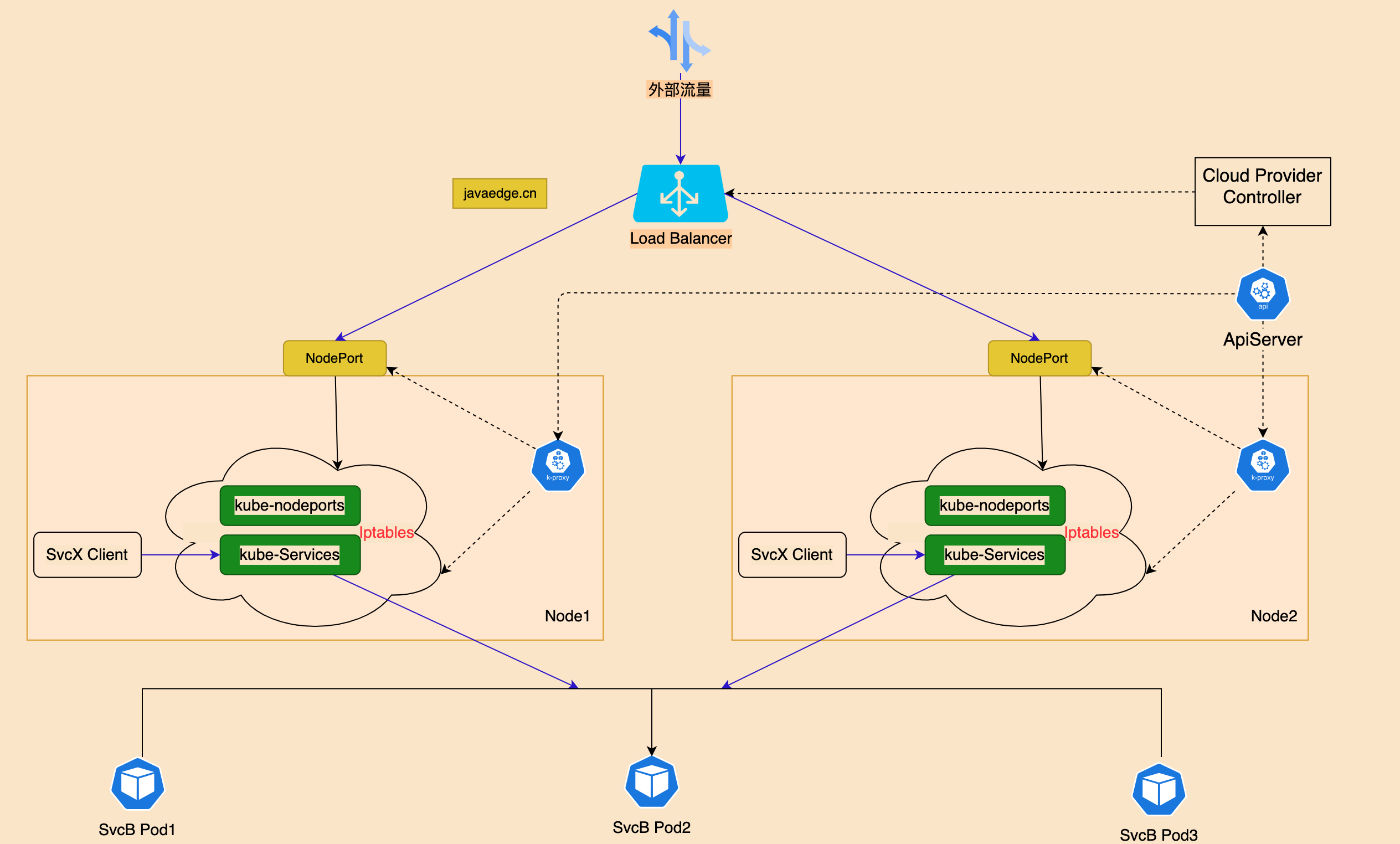
图解Kubernetes的服务(Service)
pod 准备: 不要直接使用和管理Pods: 当使用ReplicaSet水平扩展scale时,Pods可能被terminated当使用Deployment时,去更新Docker Image Version,旧Pods会被terminated,然后创建新Pods 0 啥是服务…...

facebook广告素材制作要注意哪些
在制作Facebook广告素材时,需要注意以下几点: 目标受众:了解目标受众的喜好、需求和兴趣,以便制作能够吸引他们的广告素材。广告格式:选择适合广告内容的格式,如图片、视频、幻灯片等。同时,要…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
