代码随想录算法训练营第17天 | 110.平衡二叉树 + 257. 二叉树的所有路径 + 404.左叶子之和
今日内容
- 110.平衡二叉树
- 257. 二叉树的所有路径
- 404.左叶子之和
110.平衡二叉树 - Easy
题目链接:. - 力扣(LeetCode)
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
思路:递归法,注意区分深度和高度
class Solution {
public:// 返回以该节点为根节点的二叉树的高度,如果不是平衡二叉树了则返回-1int getHeight(TreeNode* node) {if (node == NULL) {return 0;}int leftHeight = getHeight(node->left);if (leftHeight == -1) return -1;int rightHeight = getHeight(node->right);if (rightHeight == -1) return -1;return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);}bool isBalanced(TreeNode* root) {return getHeight(root) == -1 ? false : true;}
};

257. 二叉树的所有路径 - Easy
题目链接:力扣-257. 二叉树的所有路径
给你一个二叉树的根节点
root,按 任意顺序 ,返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。
思路:递归法,其实实现的是回溯
class Solution {
private:void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {path.push_back(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中 // 这才到了叶子节点if (cur->left == NULL && cur->right == NULL) {string sPath;for (int i = 0; i < path.size() - 1; i++) {sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]);result.push_back(sPath);return;}if (cur->left) { // 左 traversal(cur->left, path, result);path.pop_back(); // 回溯}if (cur->right) { // 右traversal(cur->right, path, result);path.pop_back(); // 回溯}}public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if (root == NULL) return result;traversal(root, path, result);return result;}
};
404.左叶子之和 - Easy
题目链接:力扣-404. 左叶子之和
给定二叉树的根节点
root,返回所有左叶子之和。
思路:递归法
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right== NULL) return 0;int leftValue = sumOfLeftLeaves(root->left); // 左if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况leftValue = root->left->val;}int rightValue = sumOfLeftLeaves(root->right); // 右int sum = leftValue + rightValue; // 中return sum;}
};

今日总结
第一题注意区分高度和深度,第二题回溯搞得不是很明白
相关文章:

代码随想录算法训练营第17天 | 110.平衡二叉树 + 257. 二叉树的所有路径 + 404.左叶子之和
今日内容 110.平衡二叉树 257. 二叉树的所有路径 404.左叶子之和 110.平衡二叉树 - Easy 题目链接:. - 力扣(LeetCode) 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为࿱…...
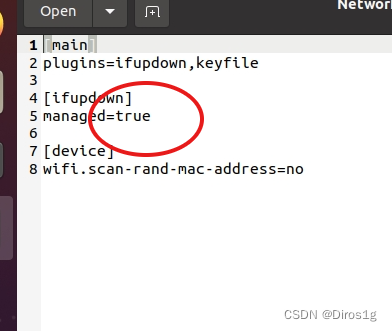
ubuntu20.04网络问题以及解决方案
1.网络图标消失,wired消失,ens33消失 参考:https://blog.51cto.com/u_204222/2465609 https://blog.csdn.net/qq_42265170/article/details/123640669 原始是在虚拟机中切换网络连接方式(桥接和NAT), 解决…...

Java面试题(java高级面试题)
线程池的核心线程数设置为多大比较合理? Worker线程在执行的过程中,有一部计算时间需要占用CPU,另一部分等待时间不需要占用CPU,通过量化分析,例如打日志进行统计,可以统计出整个Worker线程执行过程中这两…...

【MIdjourney】关于图像中人物视角的关键词
本篇仅是我个人在使用过程中的一些经验之谈,不代表一定是对的,如有任何问题欢迎在评论区指正,如有补充也欢迎在评论区留言。 1.全景镜头(panorama) 全景镜头是一种广角镜头,可以捕捉到比普通镜头更广阔的视野范围。全景镜头&…...
)
433. 最小基因变化(Queue使用ArrayList和LinkedList进行声明)
这道题可以看成一个24叉树。 因为基因序列长度固定为8,且每个位置的字母固定是AGCT,可以选择改变的只有3个字母,所以一次最多24种情况。 然后检查变化后的结果是否存在bank中(使用hashSet来存储),同时设置…...

MYSQL双主节点–更换ip
MYSQL双主节点–更换ip 一、更换双主节点ip 1.停止mysql服务 #安装了supervisor supervisorctl stop mysql #未安装 systemctl stop mysqld2.修改网卡配置信息 注:ens33是网卡名称,可能网卡不叫ens33 vi /etc/sysconfig/network-scripts/ifcfg-ens333…...

一文玩转Go语言中的面向对象编程~
温故而知新:什么是面向对象 面向对象(Object-Oriented)是一种计算机编程的方法和思想,它将程序中的数据(对象)和操作(方法)组织成一个个相互关联和交互的对象。对象是现实世界中的事…...

kylin集群反向代理(健康检查)
前面一篇文章提到了使用nginx来对kylin集群进行反向代理, kylin集群使用nginx反向代理-CSDN博客文章浏览阅读349次,点赞8次,收藏9次。由于是同一个集群的,元数据没有变化,所以,直接将原本的kylin使用scp的…...
【docker】centos7安装harbor
目录 零、前提一、下载离线包二、安装三、访问四、开机自启 零、前提 1.前提是已经安装了docker和docker-compose 一、下载离线包 1. csdn资源:harbor-offline-installer-v2.10.0.tgz 2. 百度云盘(提取码:ap3t):harbo…...

2024 年 1 月安全更新修补了 58 个漏洞(Android )
谷歌发布了针对 Android 平台 58 个漏洞的补丁,并修复了 Pixel 设备中的 3 个安全漏洞,拉开了 2024 年的序幕。 Android 2024 年 1 月更新的第一部分以 2024 年 1 月 1 日安全补丁级别发布在设备上,解决了框架和系统组件中的 10 个安全漏洞&…...

数据库系统概念 第七版 中文答案 第3章 SQL介绍
3.1 将以下查询使用SQL语言编写,使用大学数据库模式。 (我们建议您实际在数据库上运行这些查询,使用我们在书籍网站db-book.com上提供的示例数据。有关设置数据库和加载示例数据的说明,请参阅上述网站。) a. 查找计算机…...

什么是数通技术?以太网交换机在数通技术中的精要
什么是数通技术? 数通技术是指数字通信技术,它涵盖了数字信号处理、数据传输、网络通信等领域。通信工程师在数通技术中负责设计、建设和维护数字通信系统,以实现可靠、高效的信息传输。这涉及到数字信号的编解码、调制解调、数据压缩、网络…...

php 的数学常用函数
目录 1.常用列表 2.代码示例 1.常用列表 函数名描述输入输出abs()求绝对值数字绝对值数字ceil()进一法取整浮点数进一取整floor()舍去法求整浮点数直接舍去小数部分fmod()浮点数取余 两个浮点 数,x>y 浮点余数 pow()返回数的n次方基础数n次方乘方值round()浮点数四舍五入…...

Netty-Netty组件了解
EventLoop 和 EventLoopGroup 回想一下我们在 NIO 中是如何处理我们关心的事件的?在一个 while 循环中 select 出事 件,然后依次处理每种事件。我们可以把它称为事件循环,这就是 EventLoop 。 interface io.netty.channel. EventLoo…...

银行的压力测试如何进行?
为什么要进行压力风险测试? 压力风险测试的最终目的是测试银行在极度恶劣的市场环境中是否有足够的资本维持运转。 题主链接中的一级资本充足率(Tier 1 capital ratio) 亦即衡量标准,这个数字越大,表明银行资本约充裕,可以在停止…...

QtService、托盘程序使用
1、QtService 使用QtService实现Qt后台服务程序 用QT创建一个Windows Service以及踩到的若干坑 2、托盘程序 Qt之程序最小化托盘显示及操作 Qt系统托盘程序的实现...

使用Linux防火墙管理HTTP流量
在Linux系统中,防火墙是用于控制网络流量的重要工具。通过防火墙,你可以根据需要限制、过滤或允许特定的网络流量,从而提高系统的安全性。在处理HTTP流量时,防火墙可以帮助你实施访问控制、流量监控和其他安全策略。 iptables i…...
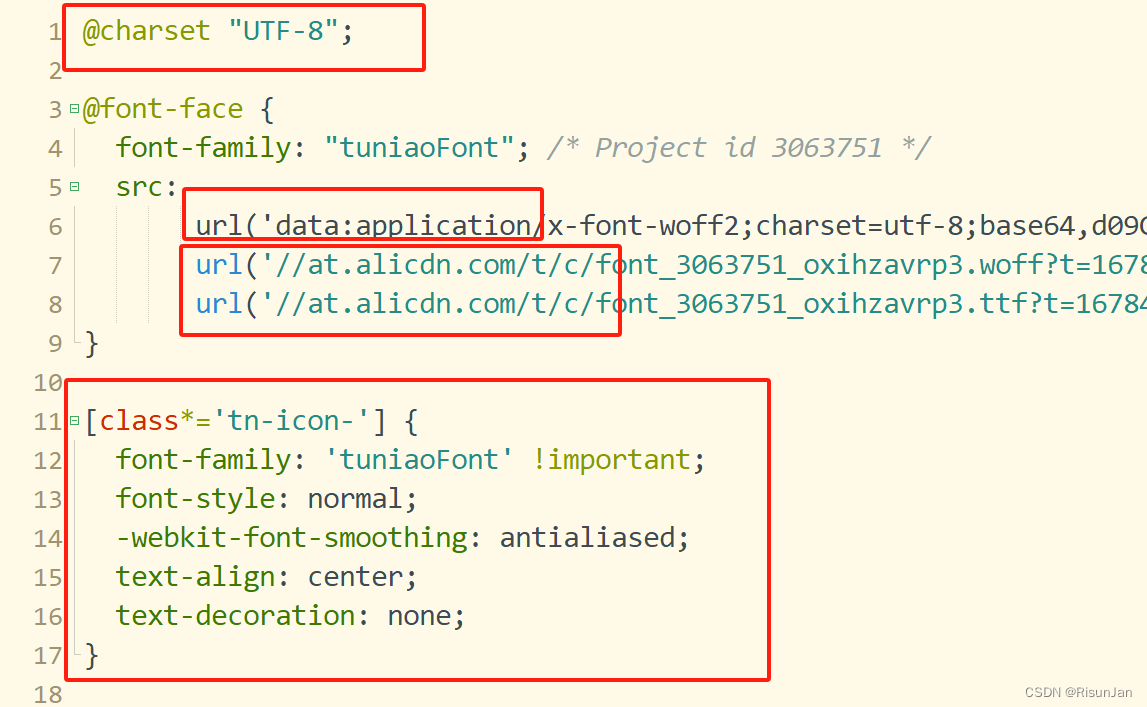
图鸟引入多套字体图标的方式教程
https://www.yuque.com/tuniao/qunyou/tgfvpg ①上传icon,生成iconfont.css 将css文件放这里 app.vue全局引入 适当改造iconfont.css的写法,方便调用...

在openEuler环境下快速编译GreatSQL RPM包
在上一篇中,已经介绍了在CentOS环境下编译GreatSQL RPM包的过程,本文再介绍如何在openEuler环境下编译GreatSQL RPM包。 运行环境是docker中的openEuler 22.03 x86_64: $ docker -v Docker version 20.10.10, build b485636$ docker run -itd…...
C语言基础语法跟练 day3
31、不使用累计乘法的基础上,通过移位运算(<<)实现2的n次方的计算。 #include <stdio.h> int main() {int i 0;scanf("%d",&i);printf("%d",1<<i);return 0; } 32、问题:一年约有 3.…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
