【机器学习】常见算法详解第2篇:K近邻算法各种距离度量(已分享,附代码)

本系列文章md笔记(已分享)主要讨论机器学习算法相关知识。机器学习算法文章笔记以算法、案例为驱动的学习,伴随浅显易懂的数学知识,让大家掌握机器学习常见算法原理,应用Scikit-learn实现机器学习算法的应用,结合场景解决实际问题。包括K-近邻算法,线性回归,逻辑回归,决策树算法,集成学习,聚类算法。K-近邻算法的距离公式,应用LinearRegression或SGDRegressor实现回归预测,应用LogisticRegression实现逻辑回归预测,应用DecisionTreeClassifier实现决策树分类,应用RandomForestClassifie实现随机森林算法,应用Kmeans实现聚类任务。
全套笔记和代码自取地址: https://gitee.com/yinuo112/Technology/tree/master/机器学习/机器学习(算法篇)/1.md
感兴趣的小伙伴可以自取哦,欢迎大家点赞转发~
共 7 章,44 子模块,总字数:52595


K-近邻算法
学习目标
- 掌握K-近邻算法实现过程
- 知道K-近邻算法的距离公式
- 知道K-近邻算法的超参数K值以及取值问题
- 知道kd树实现搜索的过程
- 应用KNeighborsClassifier实现分类
- 知道K-近邻算法的优缺点
- 知道交叉验证实现过程
- 知道超参数搜索过程
- 应用GridSearchCV实现算法参数的调优
1.3 距离度量
1 欧式距离**(Euclidean Distance):**
欧氏距离是最容易直观理解的距离度量方法,我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。

举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 1.4142 2.8284 4.2426 1.4142 2.8284 1.4142
2 曼哈顿距离(Manhattan Distance):
在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。


举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 2 4 6 2 4 2
3 切比雪夫距离 (Chebyshev Distance):
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。

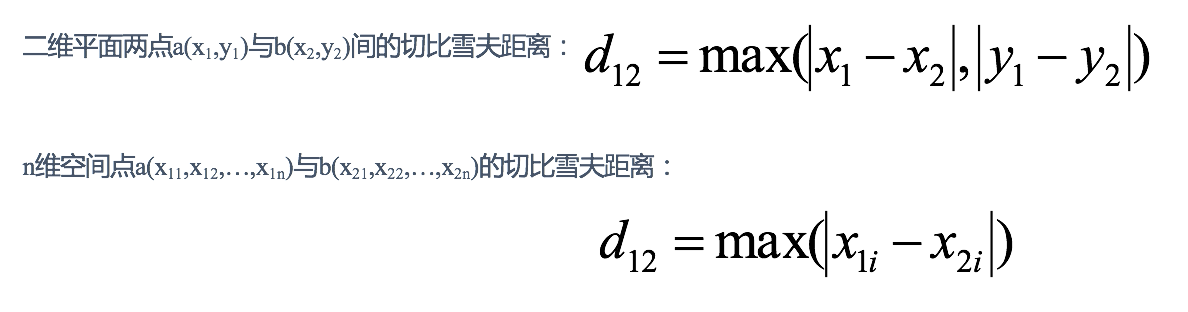
举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 1 2 3 1 2 1
4 闵可夫斯基距离(Minkowski Distance):
闵氏距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。
两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为:
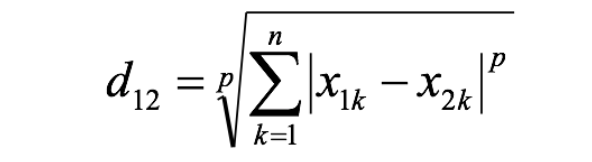
其中p是一个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧氏距离;
当p→∞时,就是切比雪夫距离。
根据p的不同,闵氏距离可以表示某一类/种的距离。
小结:
1 闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:
e.g. 二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本:a(180,50),b(190,50),c(180,60)。
a与b的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c的闵氏距离。但实际上身高的10cm并不能和体重的10kg划等号。
2 闵氏距离的缺点:
(1)将各个分量的量纲(scale),也就是“单位”相同的看待了;
(2)未考虑各个分量的分布(期望,方差等)可能是不同的。
5 标准化欧氏距离 (Standardized EuclideanDistance):
标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。
思路:既然数据各维分量的分布不一样,那先将各个分量都“标准化”到均值、方差相等。假设样本集X的均值(mean)为m,标准差(standard deviation)为s,X的“标准化变量”表示为:
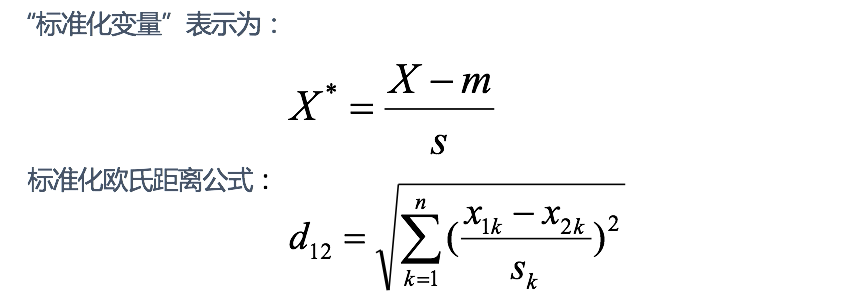
如果将方差的倒数看成一个权重,也可称之为加权欧氏距离(Weighted Euclidean distance)。
举例:
X=[[1,1],[2,2],[3,3],[4,4]];(假设两个分量的标准差分别为0.5和1)
经计算得:
d = 2.2361 4.4721 6.7082 2.2361 4.4721 2.2361
6 余弦距离(Cosine Distance)
几何中,夹角余弦可用来衡量两个向量方向的差异;机器学习中,借用这一概念来衡量样本向量之间的差异。
- 二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式:
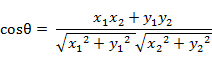
- 两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为:
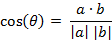
即:
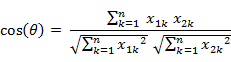
夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小,余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1,当两个向量的方向完全相反余弦取最小值-1。
举例:
X=[[1,1],[1,2],[2,5],[1,-4]]
经计算得:
d = 0.9487 0.9191 -0.5145 0.9965 -0.7593 -0.8107
7 汉明距离(Hamming Distance)【了解】:
两个等长字符串s1与s2的汉明距离为:将其中一个变为另外一个所需要作的最小字符替换次数。
例如:
The Hamming distance between "1011101" and "1001001" is 2. The Hamming distance between "2143896" and "2233796" is 3. The Hamming distance between "toned" and "roses" is 3.
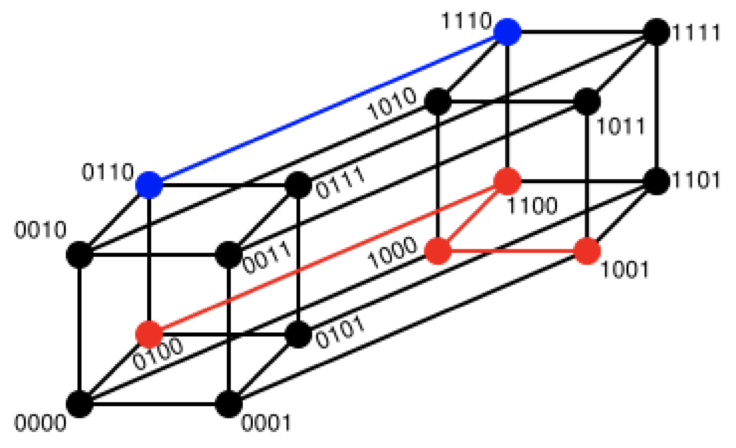
随堂练习:
求下列字符串的汉明距离:1011101与 1001001 2143896与 2233796 irie与 rise
汉明重量:是字符串相对于同样长度的零字符串的汉明距离,也就是说,它是字符串中非零的元素个数:对于二进制字符串来说,就是 1 的个数,所以 11101 的汉明重量是 4。因此,如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。
应用:汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中,为了增强容错性,应使得编码间的最小汉明距离尽可能大。但是,如果要比较两个不同长度的字符串,不仅要进行替换,而且要进行插入与删除的运算,在这种场合下,通常使用更加复杂的编辑距离等算法。
举例:
X=[[0,1,1],[1,1,2],[1,5,2]]
注:以下计算方式中,把2个向量之间的汉明距离定义为2个向量不同的分量所占的百分比。经计算得:
d = 0.6667 1.0000 0.3333
8 杰卡德距离(Jaccard Distance)【了解】:
杰卡德相似系数(Jaccard similarity coefficient):两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示:
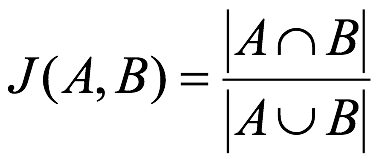
杰卡德距离(Jaccard Distance):与杰卡德相似系数相反,用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度:
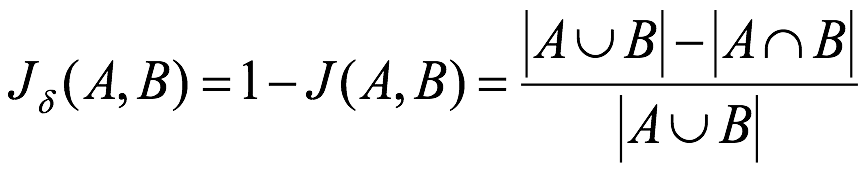
举例:
X=[[1,1,0][1,-1,0],[-1,1,0]]
注:以下计算中,把杰卡德距离定义为不同的维度的个数占“非全零维度”的比例
经计算得:
d = 0.5000 0.5000 1.0000
9 马氏距离(Mahalanobis Distance)【了解】
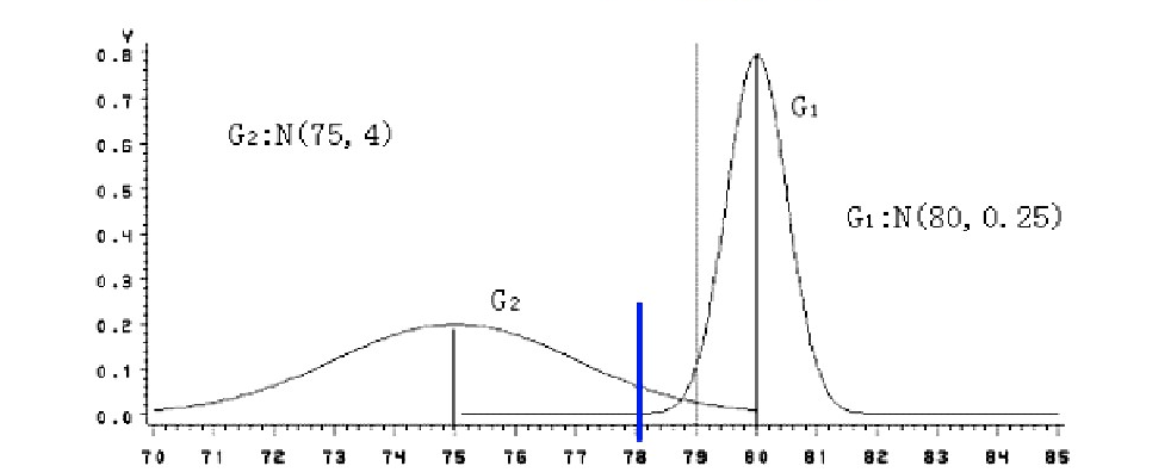
下图有两个正态分布图,它们的均值分别为a和b,但方差不一样,则图中的A点离哪个总体更近?或者说A有更大的概率属于谁?显然,A离左边的更近,A属于左边总体的概率更大,尽管A与a的欧式距离远一些。这就是马氏距离的直观解释。
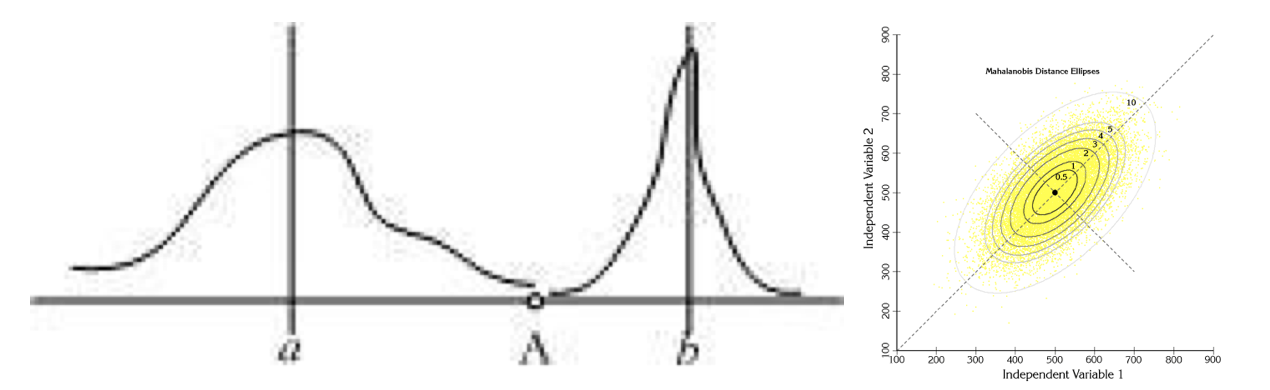
马氏距离是基于样本分布的一种距离。
马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。它是一种有效的计算两个位置样本集的相似度的方法。
与欧式距离不同的是,它考虑到各种特性之间的联系,即独立于测量尺度。
**马氏距离定义:**设总体G为m维总体(考察m个指标),均值向量为μ=(μ1,μ2,… …,μm,)`,协方差阵为∑=(σij),
则样本X=(X1,X2,… …,Xm,)`与总体G的马氏距离定义为:
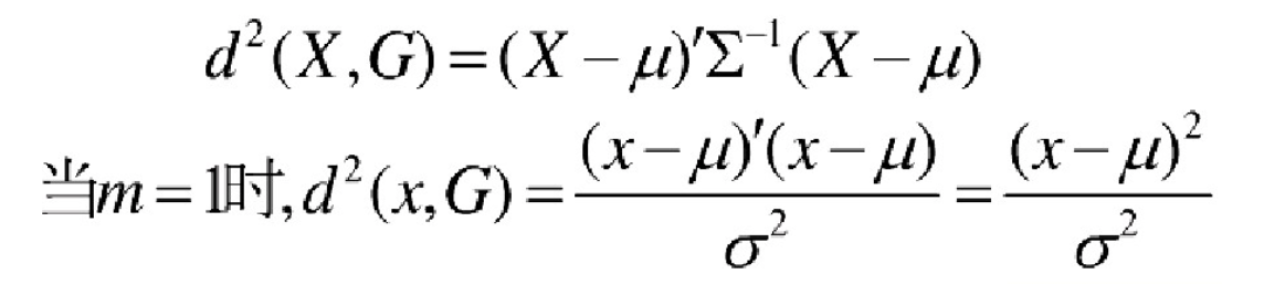
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为∑的随机变量的差异程度:如果协方差矩阵为单位矩阵,马氏距离就简化为欧式距离;如果协方差矩阵为对角矩阵,则其也可称为正规化的欧式距离。
马氏距离特性:
1.量纲无关,排除变量之间的相关性的干扰;
2.马氏距离的计算是建立在总体样本的基础上的,如果拿同样的两个样本,放入两个不同的总体中,最后计算得出的两个样本间的马氏距离通常是不相同的,除非这两个总体的协方差矩阵碰巧相同;
3 .计算马氏距离过程中,要求总体样本数大于样本的维数,否则得到的总体样本协方差矩阵逆矩阵不存在,这种情况下,用欧式距离计算即可。
4.还有一种情况,满足了条件总体样本数大于样本的维数,但是协方差矩阵的逆矩阵仍然不存在,比如三个样本点(3,4),(5,6),(7,8),这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下,也采用欧式距离计算。
欧式距离&马氏距离:
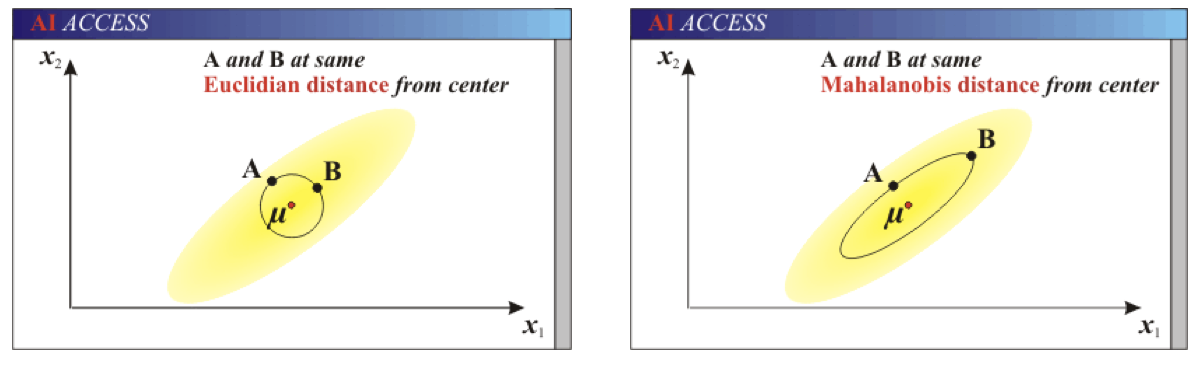
举例:
已知有两个类G1和G2,比如G1是设备A生产的产品,G2是设备B生产的同类产品。设备A的产品质量高(如考察指标为耐磨度X),其平均耐磨度μ1=80,反映设备精度的方差σ2(1)=0.25;设备B的产品质量稍差,其平均耐磨损度μ2=75,反映设备精度的方差σ2(2)=4.
今有一产品G0,测的耐磨损度X0=78,试判断该产品是哪一台设备生产的?
直观地看,X0与μ1(设备A)的绝对距离近些,按距离最近的原则,是否应把该产品判断设备A生产的?
考虑一种相对于分散性的距离,记X0与G1,G2的相对距离为d1,d2,则:
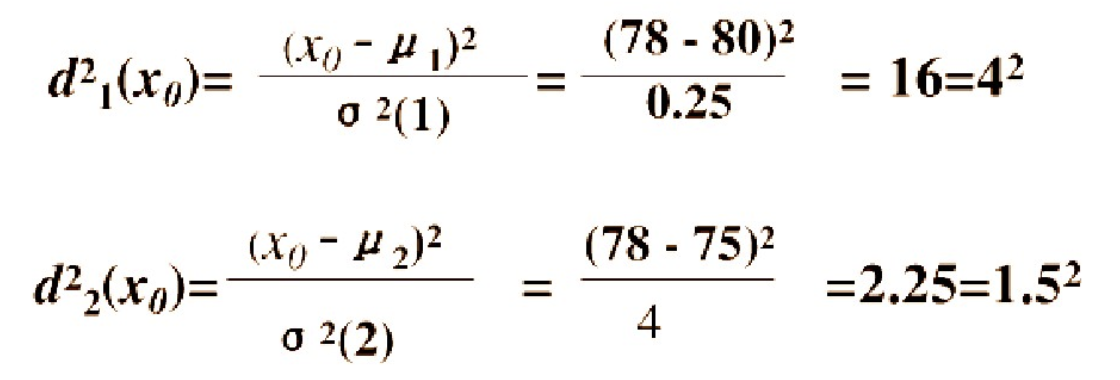
因为d2=1.5 < d1=4,按这种距离准则,应判断X0为设备B生产的。
设备B生产的产品质量较分散,出现X0为78的可能性较大;而设备A生产的产品质量较集中,出现X0为78的可能性较小。
这种相对于分散性的距离判断就是马氏距离。
未完待续, 同学们请等待下一期
相关文章:

【机器学习】常见算法详解第2篇:K近邻算法各种距离度量(已分享,附代码)
本系列文章md笔记(已分享)主要讨论机器学习算法相关知识。机器学习算法文章笔记以算法、案例为驱动的学习,伴随浅显易懂的数学知识,让大家掌握机器学习常见算法原理,应用Scikit-learn实现机器学习算法的应用࿰…...

@KafkaListener指定kafka集群
基于KafkaListener注解的kafka监听代码可以手动指定要消费的kafka集群,这对于需要访问多套kafka集群的程序来说,是有效的解决方案。这里需要注意的是,此时的消费者配置信息需使用原生kafka的配置信息格式(如:ConsumerC…...

什么是算法的空间复杂度?
一、问题 常常⽤算法的空间复杂度来评价算法的性能,那么什么是算法的空间复杂度呢? 二、解答 算法的空间复杂度是指在算法的执⾏过程中,需要的辅助空间数量。 辅助空间数量指的不是程序指令、常数、指针等所需要的存储空间,也不是…...
WebDav协议相关软件@简单配置局域网内的http和WebDav服务器和传输系统
文章目录 相关软件windows自带第三方软件 chfs(CuteHttpFileServer)下载软件GUI方案 补充命令行方案命令行程序定位简单创建服务站点使用配置文件配置细节 使用软连接或符号链接等手段将向共享站点的根目录添加文件开机自启服务包装nssm包装使用powershell包装 服务启动chfs服务…...

自定义数据实现SA3D
SA3D:Segment Anything in 3D with NeRFs 实现了3D目标分割 原理是利用SAM(segment anything) 模型和Nerf分割渲染3D目标, SAM只能分块,是没有语义标签的,如何做到语义连续? SA3D中用了self-prompt, 根据前一帧的mask…...

设计模式基础概念:探索设计模式的魅力
设计模式是软件开发中的一种指导性概念,它提供了一套被广泛接受的解决方案,用于常见的设计问题。设计模式有助于提高软件的可重用性、可扩展性和可维护性,并促进团队之间的沟通。 以下是一些常见的设计模式: 创建型模式࿱…...

【Leetcode】2182. 构造限制重复的字符串
文章目录 题目思路代码 题目 2182. 构造限制重复的字符串 问题:给你一个字符串 s 和一个整数 repeatLimit ,用 s 中的字符构造一个新字符串 repeatLimitedString ,使任何字母 连续 出现的次数都不超过 repeatLimit 次。你不必使用 s 中的全…...
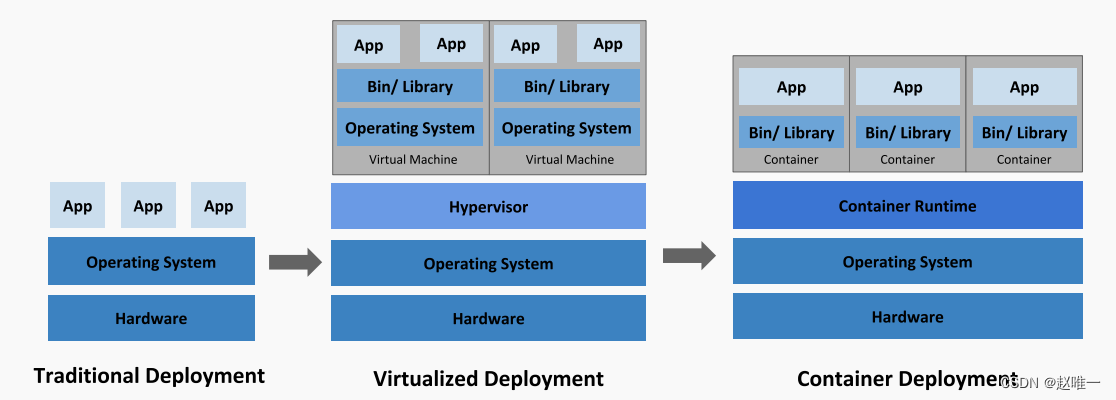
Kubernetes(K8S)云服务器实操TKE
一、 Kubernetes(K8S)简介 Kubernetes源于希腊语,意为舵手,因为首尾字母中间正好有8个字母,简称为K8S。Kubernetes是当今最流行的开源容器管理平台,是 Google 发起并维护的基于 Docker 的开源容器集群管理系统。它是大名鼎鼎的Google Borg的开源版本。 K8s构建在 Docker …...

设置弹窗随鼠标位置移动
1.这是要移动的弹窗,隐藏显示逻辑、样式、展示内容自己写,主要就是动态设置弹窗的style,floatLeft和floatTop都是Vue中的data双向绑定数据; <div id"box" v-show"hasMove" :style"{ left: floatLeft…...

Spring Boot实现数据加密脱敏:注解 + 反射 + AOP
文章目录 1. 引言2. 数据加密和脱敏的需求3. Spring Boot项目初始化4. 敏感数据加密注解设计5. 实现加密和脱敏的工具类6. 实体类和加密脱敏注解的使用7. 利用AOP实现加密和脱敏8. 完善AOP切面9. 测试10. 拓展功能与未来展望10.1 加密算法的选择10.2 动态注解配置 11. 总结 &am…...
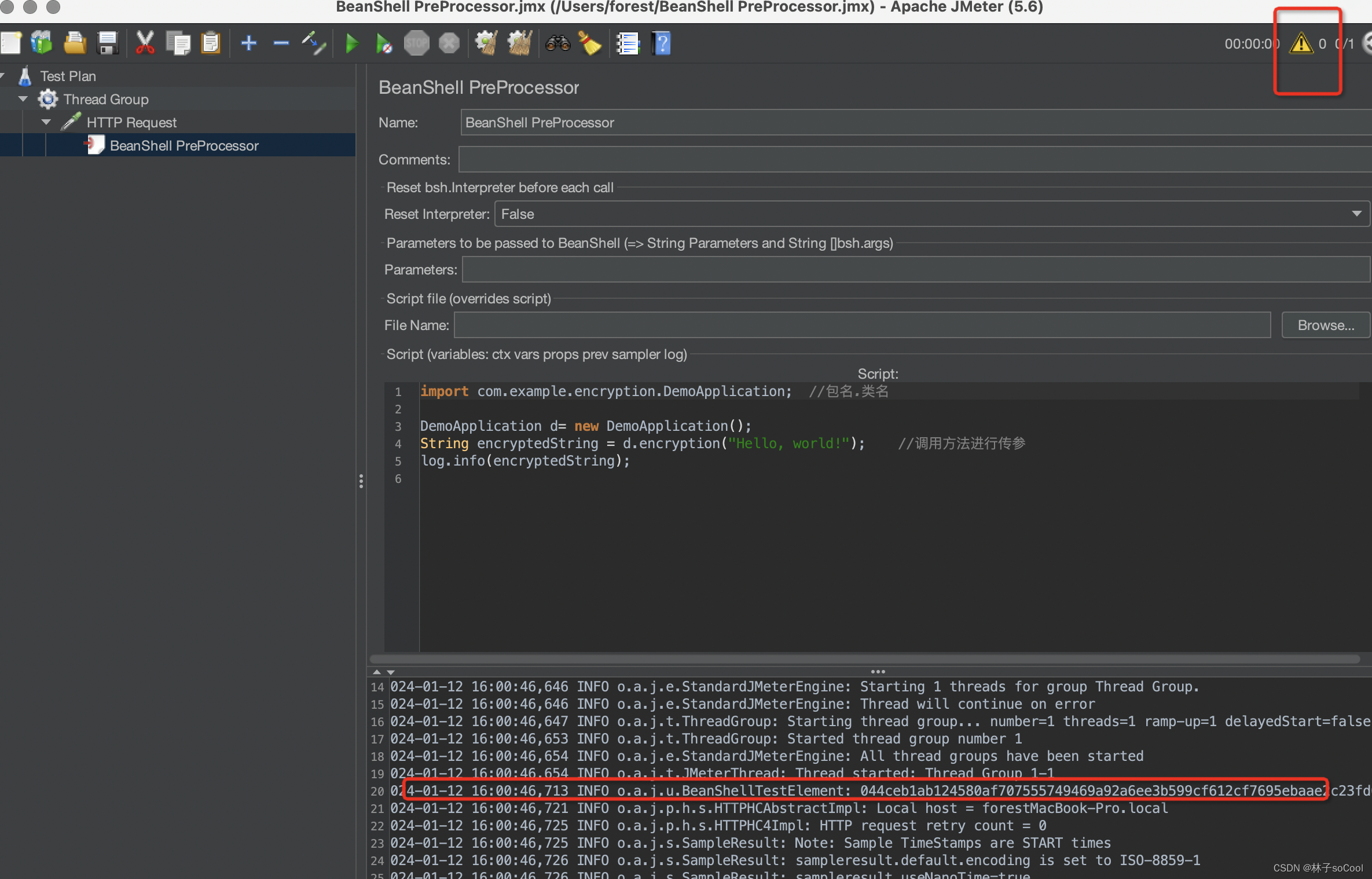
jmeter和meterSphere如何使用第三方jar包
工具引用jar包语言都是beanshell 问题起因:metersphere 接口自动化实现过程中,如何实现字符串加密且加密方法依赖第三方库; 使用语言:beanshell脚本语言,java语言 使用工具:idea jmeter metersphere 1.首…...
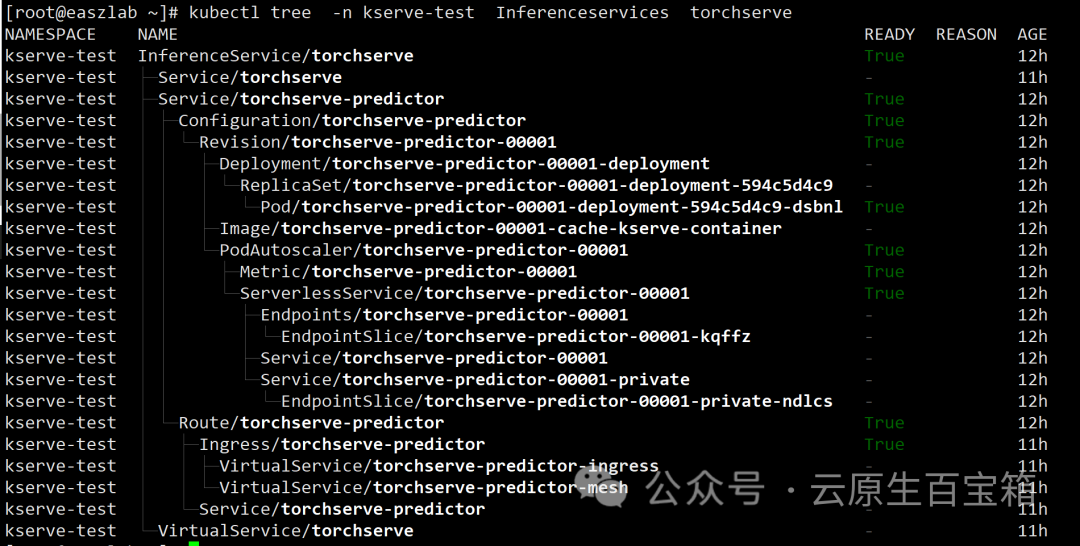
API对象上千个,有啥关联性,kubectl-tree一键搞定
关注【云原生百宝箱】公众号,获取更多云原生消息 "kubectl-tree 是一款强大的 kubectl 插件,通过 ownerReferences 实现 Kubernetes 对象之间的所有权关系探索。相较于 kubectl lineage,它不仅更全面理解 API 对象的逻辑关系,…...

java自定义工具类在List快速查找相同字段值对象
根据对象某一字段名,获取字段值,将List转换为Map中包含list,Key为字段值,Value为相同字段值的对象list,快速定位具有相同字段值的对象,转换之后便于在Map中根据字段值快速查找相同字段值的对象 //List转Map…...

codeforces Hello 2024 - C - Grouping Increases --- 题解
目录 Grouping Increases 题目描述: 思路解析: 代码实现: Grouping Increases 题目描述: 给你一个大小为n的数组a,你可以把数组a划分为两个子序列s和t,a中元素,要么在子序列s中,…...
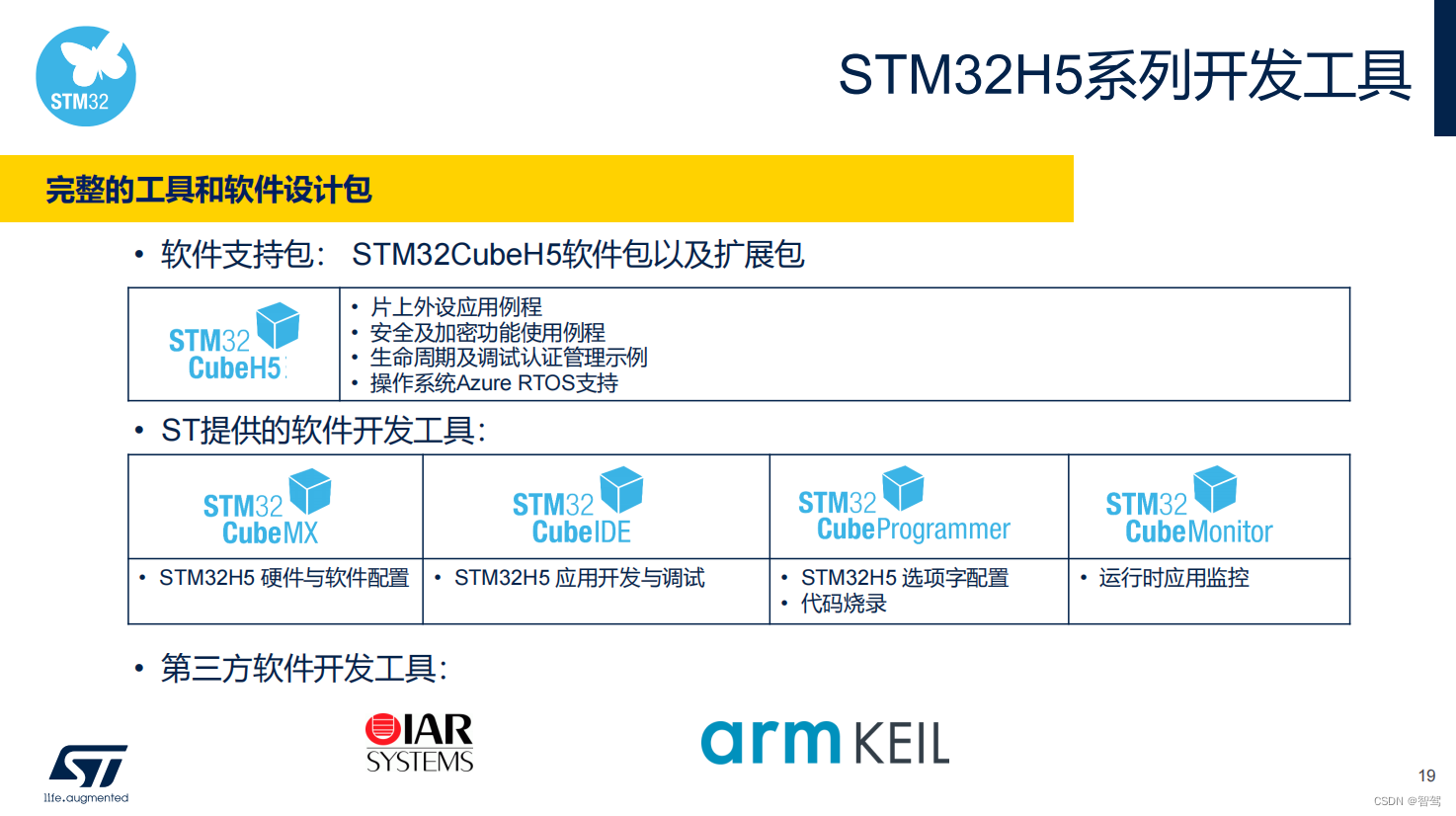
STM32H5培训(一)总览
文章目录 1. 前言2. STM32H5系列MCU的特点和新功能包括性能提升、新外设和安全功能等3. STM32H5系列型号之间的区别和关键资源对比4. 性能和功能亮点6. 开发生态参考: 1. 前言 本篇主要介绍STM32H5系列MCU的特点和新功能,包括全新的M33内核、250M主频处…...

亚马逊云科技 WAF 部署小指南(五):在客户端集成 Amazon WAF SDK 抵御 DDoS 攻击...
方案介绍 在 WAF 部署小指南(一)中,我们了解了 Amazon WAF 的原理,并通过创建 WEB ACL 和托管规则防护常见的攻击。也了解了通过创建自定义规则在 HTTP 请求到达应用之前判断是阻断还是允许该请求。在 Amazon WAF 自定义规则中&am…...
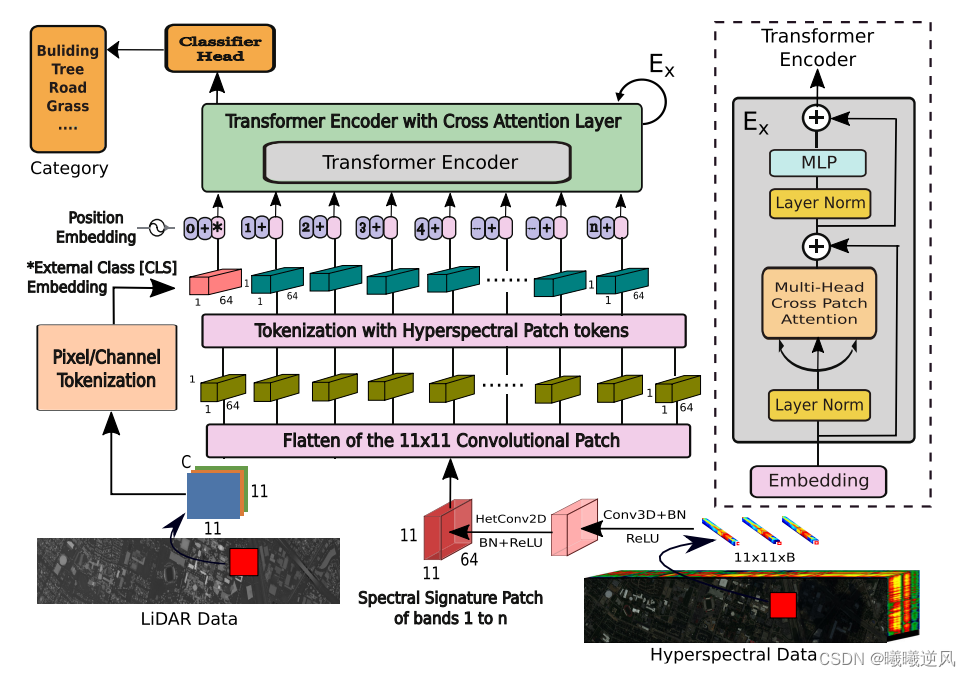
高光谱分类论文解读分享之基于多模态融合Transformer的遥感图像分类方法
IEEE TGRS 2023:基于多模态融合Transformer的遥感图像分类方法 题目 Multimodal Fusion Transformer for Remote Sensing Image Classification 作者 Swalpa Kumar Roy , Student Member, IEEE, Ankur Deria , Danfeng Hong , Senior Member, IEEE, Behnood Ras…...
Trans论文复现:基于数据驱动的新能源充电站两阶段规划方法程序代码!
适用平台:MatlabYalmipCplex/Gurobi; 文章提出了一种电动汽车充电站的两阶段规划方法,第一阶段通过蒙特卡洛法模拟充电车辆需求和电池充放电数据来确定充电站位置;第二阶段通过数据驱动的分布鲁棒优化方法优化充电站的新能源和电池…...

将抖音视频转成MP3并下载
这篇是在上一篇的基础上写的,这篇负责抖音作者详情页的视频转声音提取,这篇需要用到后端。 本地启动后端后,在控制台输入对应代码,即可实现hover在封面上,按d一键下载音频 控制台代码 // 获取作者的视频列表var liEle…...

C程序训练:与输入有关的错误
在录入程序时有时稍不注意就可能录入错误的字符导致程序运行结果出现错误,下面举例说明。 下面程序的运行结果是错的,但程序又没有错,到底问题出现在哪呢? #include <stdio.h> int main() {FILE *fp;int i, k, n;fpfopen(…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
