机器学习100天（三十八）：038 朴素贝斯-处理离散数据
《机器学习100天》完整目录：目录
机器学习100天，今天讲的是：朴素贝斯-处理离散数据！
打开 spyder，新建一个 naive_bayes_category.py 脚本。上一节我们引入了一批西瓜样本。并使用朴素贝叶斯公式计算出一个瓜蒂脱落、圆形、青色的西瓜是熟瓜的概率。下面我们来使用 python 实现。
首先导入标准库，然后导入数据集，总共包含10个样本，特征瓜蒂用0表示脱落、1表示未脱落，特征形状用0表示圆形、1表示尖形，特征颜色用0表示深绿、1表示浅绿、2表示青色。
#------ 处理离散数据 ------#
# 导入标准库
import numpy as np# 导入数据集
# 西瓜数据
#X 瓜蒂：脱落（0）、未脱落（1）
#X 形状：圆（0）、尖（1）
#X 颜色：深绿（0）相关文章：
机器学习100天（三十八）：038 朴素贝斯-处理离散数据
《机器学习100天》完整目录：目录 机器学习100天，今天讲的是：朴素贝斯-处理离散数据！ 打开 spyder，新建一个 naive_bayes_category.py 脚本。上一节我们引入了一批西瓜样本。并使用朴素贝叶斯公式计算出一个瓜蒂脱落、圆形、青色的西瓜是熟瓜的概率。下面我们来使用 pytho…...
【3.3】指针、二分、SSM项目
二分查找 class Solution {public int search(int[] nums, int target) {int n nums.length;int left 0;int right n - 1;while(left < right){int mid left (right - left) / 2;if(nums[mid] < target){left mid 1;}else if(nums[mid] > target){right mid …...
buu [INSHack2017]rsa16m 1
题目描述： 打开的 rsa_16m 文件 ： （在此我只想说神人才找得到 c 的位置） ，这位置是真的难找啊 题目分析： 首先打开 description.md 文件，得到： 翻译下来： 当您需要真正…...
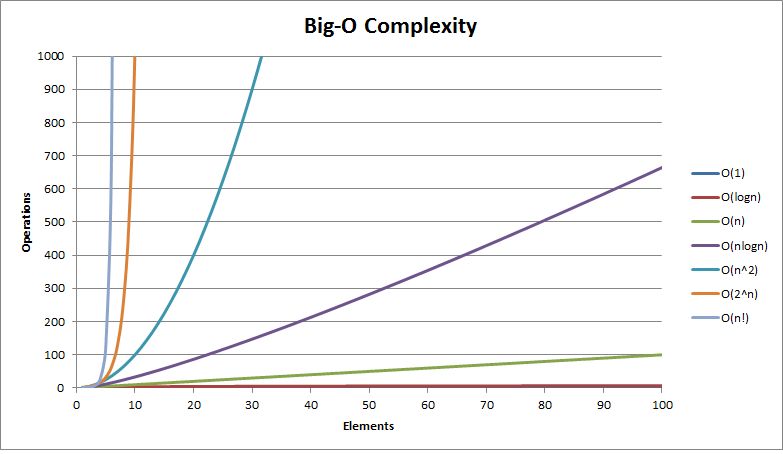
【数据结构起航】：衡量算法的好坏--时间空间复杂度
时间复杂度和空间复杂度 文章目录时间复杂度和空间复杂度1.算法效率1.1算法复杂度1.2复杂度在OJ里的应用2.时间复杂度2.1时间复杂度的概率2.2大O渐进表示法推导大O阶方法：2.3时间复杂度的举例计算3.空间复杂度3.1空间复杂度的举例计算4.复杂度各量级对比1.算法效率 …...
动手学深度学习【1】——线性回归
动手学深度学习网址：动手学深度学习 注：本部分只对基础知识进行简单的介绍并附上完整的代码实现，更多内容可参考上述网址。 简述 需要的准备知识 数学的偏导线性代数 线性模型 回归是能为一个或多个自变量与因变量之间关系建模的一类方…...
Html 相关知识
Html 相关知识 DOM 文档对象模型 (DOM) 是 HTML 和 XML 文档的编程接口。它提供了对文档的结构化的表述，并定义了一种方式可以使从程序中对该结构进行访问，从而改变文档的结构，样式和内容。DOM 将文档解析为一个由节点和对象（包…...
【冲刺蓝桥杯的最后30天】day1
大家好😃，我是想要慢慢变得优秀的向阳🌞同学👨💻，断更了整整一年，又开始恢复CSDN更新，从今天开始逐渐恢复更新状态，正在备战蓝桥杯的小伙伴可以支持一下哦！…...
c++泛型编程与模板-01函数模板
函数模板的定义 所谓函数模板，实际就是写一个通用函数，返回值和参数的类型都是可变的，用一个特定格式的变量来指定，然后调用此函数的时候，编译器会根据参数的数据类型自动推导出类型，从而达到函数再不同的…...
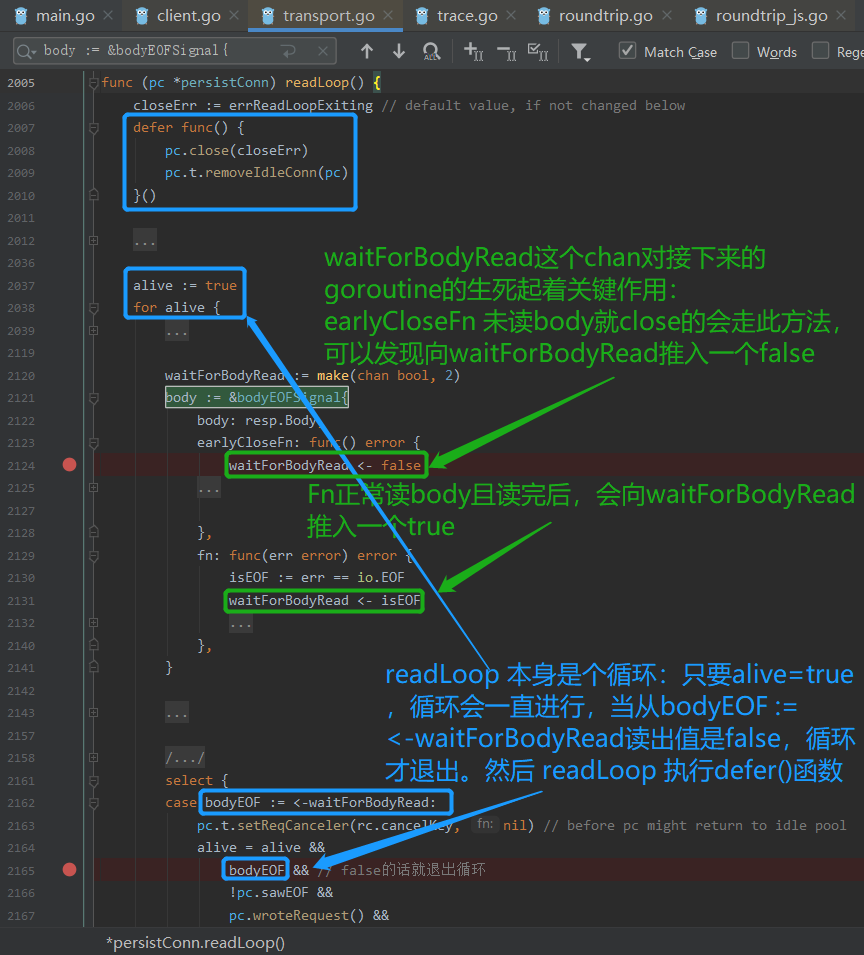
Golang http请求忘记调用resp.Body.Close()而导致的协程泄漏问题（含面试常见协程泄漏相关测试题）
参考： 知乎：别因为忘记close你的httpclient，造成goroutine泄漏 CSDN：resp.Body.Close() 引发的内存泄漏goroutine个数 先来看几道题，想一想最终的输出结果是多少呢？ package mainimport ("fmt"…...
进程信号生命周期详解
信号和信号量半毛钱关系都没有！ 每个信号都有一个编号和一个宏定义名称,这些宏定义可以在signal.h中找到,例如其中有定 义 #define SIGINT 2 查看信号的机制，如默认处理动作man 7 signal SIGINT的默认处理动作是终止进程，SIGQUIT的默认处理…...
2023-03-03干活小计
今天见识了 归一化的重要性：归一化 不容易爆炸 深度了解了学习率：其实很多操作 最后的结果都是改变了lr 以房价预测为例：一个点一个点更新 比较 矩阵的更新： 为什么小批量梯度下降 优于随机梯度下降 优于批量梯度下降ÿ…...
操作系统结构
随着操作系统的不断增多和代码规模的不断扩大，提供合理的结构对提升操作系统的安全与可靠性来说变得尤为重要。 1.分层法 指将操作系统分为若干层，最低层位硬件，最高层为用户接口，每层只能调用紧邻它的低层的功能和服务(类似于计…...
[SSD科普] 固态硬盘物理接口SATA、M.2、PCIe常见疑问，如何选择？
前言犹记得当年Windows 7系统体验指数中，那5.9分磁盘分数，在其余四项的7.9分面前，似乎已经告诉我们机械硬盘注定被时代淘汰。势如破竹的SSD固态硬盘，彻底打破了温彻斯特结构的机械硬盘多年来在电脑硬件领域的统治。SSD数倍于HDD机…...
【Java学习笔记】3.Java 基础语法
Java 基础语法 一个 Java 程序可以认为是一系列对象的集合，而这些对象通过调用彼此的方法来协同工作。下面简要介绍下类、对象、方法和实例变量的概念。 对象：对象是类的一个实例，有状态和行为。例如，一条狗是一个对象ÿ…...
Python基础学习6——if语句
基本概念 if语句为条件判断语句，用来判断if后面的语句是真是假。if的用途有很多，比如作为条件测试可以判断两数是否相等与不等、进行数值笔记等等。例子如下： Lego_price (599, 799, 898) if Lego_price[0] 599:print("Correct!&quo…...
有免费的PDF转Word吗？值得收藏的7个免费 PDF转Word工具请收好
PDF 和 DOC 是人们在工作中广泛使用的两种最流行的文档格式。PDF 是 Adobe 的便携式文档格式，DOC 是 Microsoft 的 Word 文档格式。PDF 是一种更安全可靠的文件格式，因为它很难编辑 PDF 文件，但是有一些称为 PDF 编辑器的工具可用于编辑 PDF …...
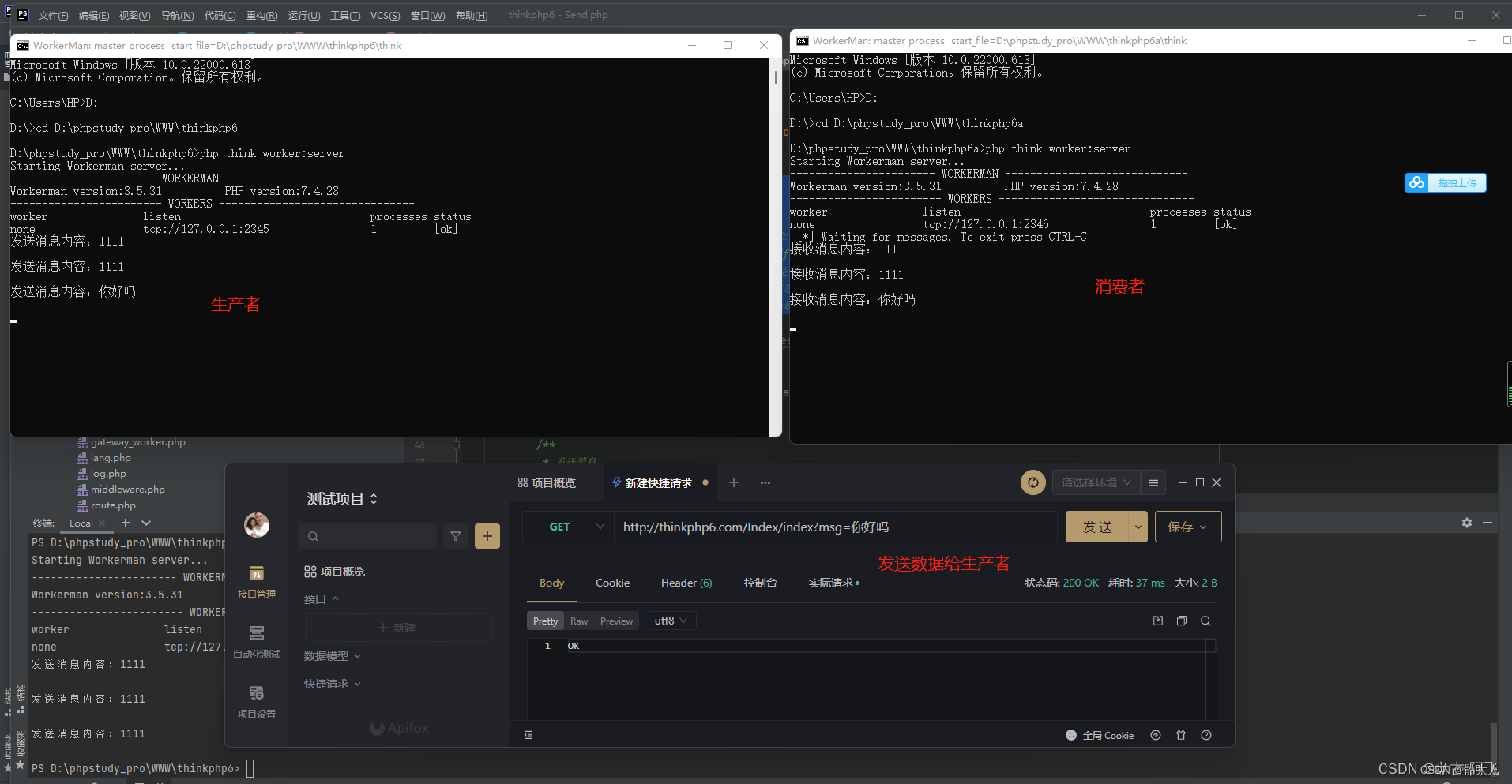
Thinkphp6使用RabbitMQ消息队列
Thinkphp6连接使用RabbitMQ（不止tp6，其他框架对应改下也一样），如何使用Docker部署RabbitMQ，在上一篇已经讲了->传送门<-。 部署环境 开始前先进入RabbitMQ的web管理界面，选择Queues菜单，点…...
小成本互联网创业怎么做？低成本创业的方法分享
多数人都会有想法创业，尤其是在互联网上面创业，很多人看到了商机，但是因为成本的原因又放弃了，实际上，小成本也可以互联网创业！那么，小成本互联网创业怎么做？低成本创业的方法在这里…...
六、栈、栈的相关问题
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 目录 前言 一、栈 1.栈概述 2.栈的实现 2.1 栈的API 2.2 栈的实现 二、栈的括号匹配问题 1.问题描述 2.代码实现 三、逆波兰表达式求值问题 1.问题描述 2.代码 总结 前言 提…...
Java安全停止线程
Thread 类虽提供了一个 stop() 方法（已经被废弃），但由于 stop() 方法强制终止一个正在执行的线程，可能会造成数据不一致的问题，所以在生产环境中最好不要使用。 场景： 由于一些操作需要轮询处理ÿ…...
应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间， 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点，不需要开启数据库闪回。…...
安宝特方案丨XRSOP人员作业标准化管理平台：AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业，其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进，需提前预防假检、错检、漏检，推动智慧生产运维系统数据的流动和现场赋能应用。同时，…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 （忘了有没有这步了 估计有） 刷机程序 和 镜像 就不提供了。要刷的时…...
高等数学（下）题型笔记（八）空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
反射获取方法和属性
Java反射获取方法 在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...
现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学（ECC）是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础，例如椭圆曲线数字签…...
06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性：使神经网络可学习复杂模式控制输出范围：如Sigmoid将输出限制在(0,1)梯度传递：影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
Go语言多线程问题
打印零与奇偶数（leetcode 1116） 方法1：使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
day36-多路IO复用
一、基本概念 （服务器多客户端模型） 定义：单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用：应用程序通常需要处理来自多条事件流中的事件，比如我现在用的电脑，需要同时处理键盘鼠标…...