python学习——【第二弹】
前言
上一篇文章 python学习——【第一弹】给大家介绍了python中的基本数据类型等,这篇文章接着学习python中的运算符的相关内容。
运算符
python中的运算符主要有:算术运算符,赋值运算符,比较运算符,布尔运算符以及位运算符。
算术运算符
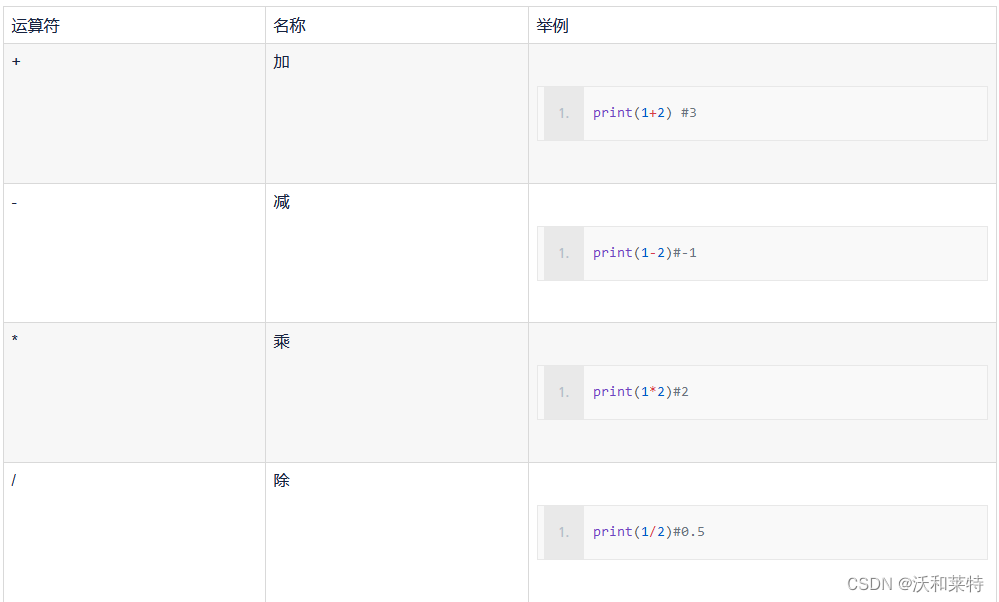
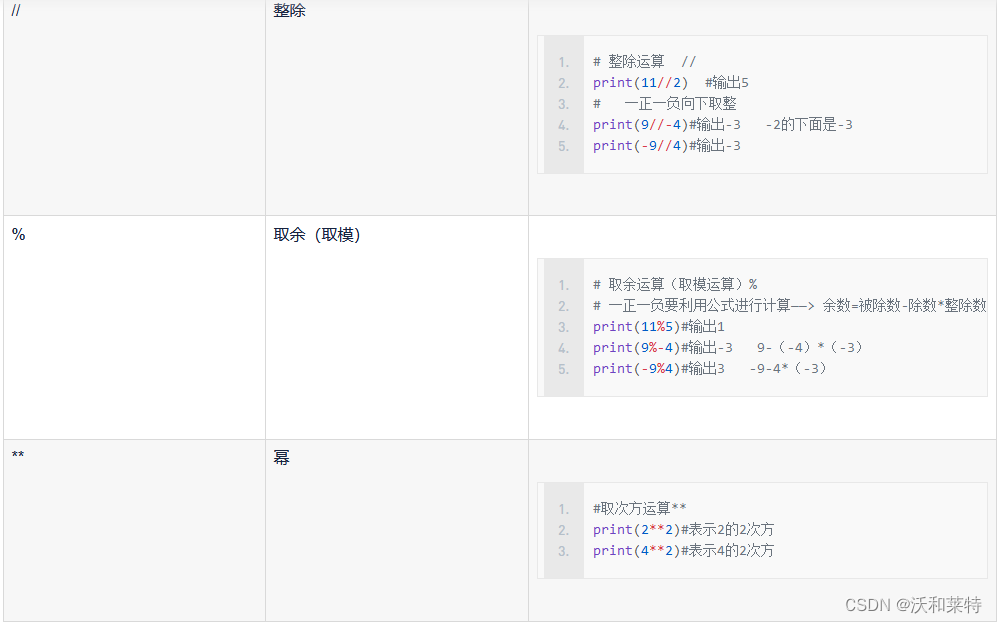
赋值运算符
1:python中的赋值运算符是由 ’ = ’ 表示的,它的执行顺序是 从右到左:
比如
a=1+2
print(a) #将1+2的值赋给等式左边的变量
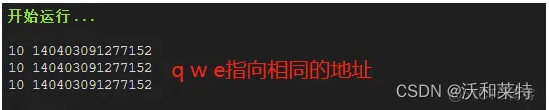
2:支持链式赋值:
q=w=e=10
print(q,id(q))
print(w,id(w))
print(e,id(e))
3:支持参数赋值
a1=20;
a1+=10
print(a1)#输出30 20+10=30
a1-=10
print(a1)#输出20 30-10=20
a1*=10
print(a1)#输出200 20*10=200
a1%=15
print(a1)#取余输出0 200%15=5
a1/=10
print(a1)#此时a1=0,故取商=0.5
b1=30
b1//=4
print(b1)#整除关系,输出7
4:支持系列解包赋值
a,b,c=10,20,30 #30-》c 20-》b 10-》a 实际上是三个对象指向三个地址
print(a,id(a))
print(b,id(b))
print(c,id(c))
#注意python是从右到左赋值,系列解包赋值指向不同的地址;并且变量的个数要和值得个数保持一致,否则会抛出ValueError:

比较运算符
1:比较运算符用的是‘ == ’比较运算符得结果是Bool类型
a,b=10,20
print('a==b吗',a==b) #False
print('a!=b吗',a!=b) #True
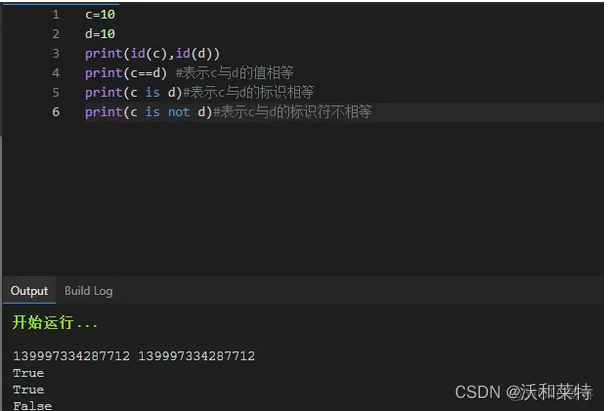
2:与赋值运算符 = 相区分 ; 比较运算符 == 比较的是两个对象得value值,不比较两个对象的标识;用于比较两个对象的标识所用得是 is,is not :
list1=[11,22,33,44]
list2=[11,22,33,44]
print(id(list1),id(list2)) #两个变量的标识不相同
print(list1==list2) #两个变量的值是相同的 True
print(list1 is list2) #False
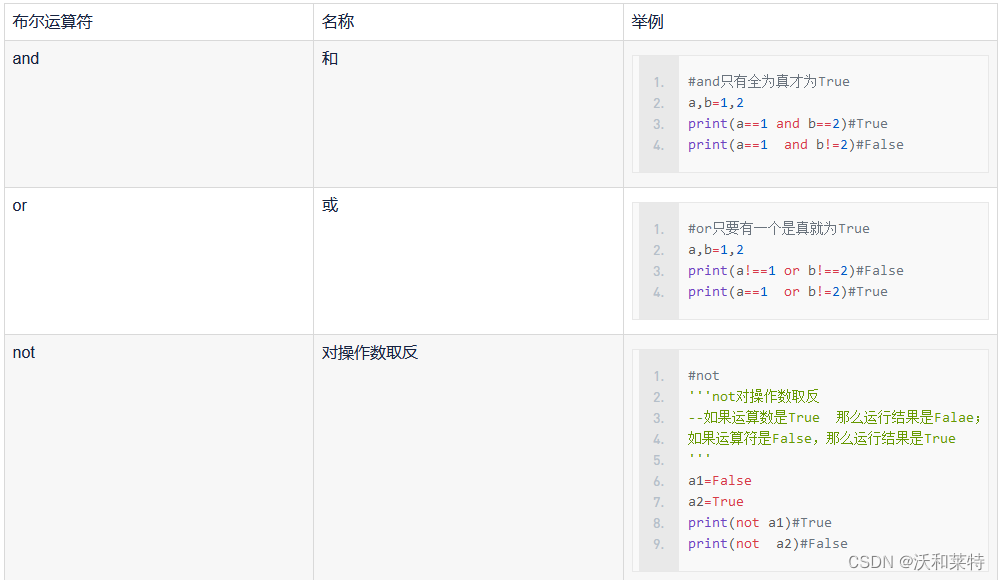
布尔运算符
使用布尔运算符返回的是True或False;以下为布尔运算符的使用说明:
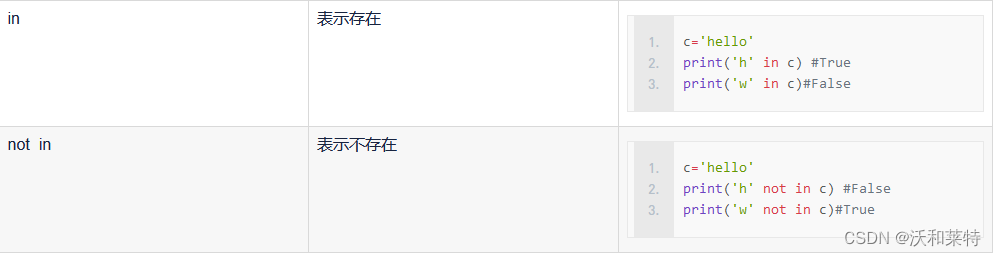
位运算符
该运算符按二进制位对值进行操作
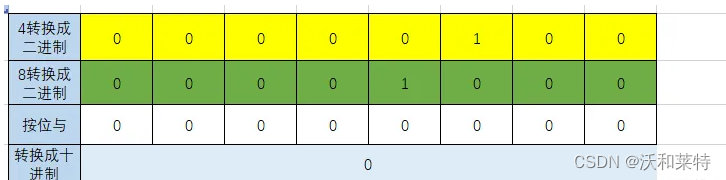
1:位与 &
参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0
print(4&8) #0
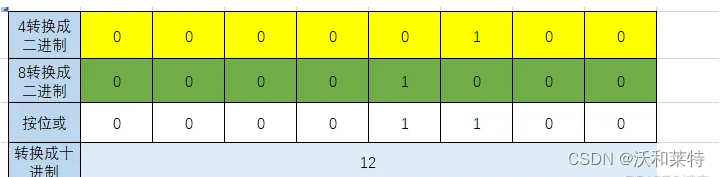
2:位或 |
只要对应的两个二进位有一个为1时,结果位就为1
print(4|8) #12
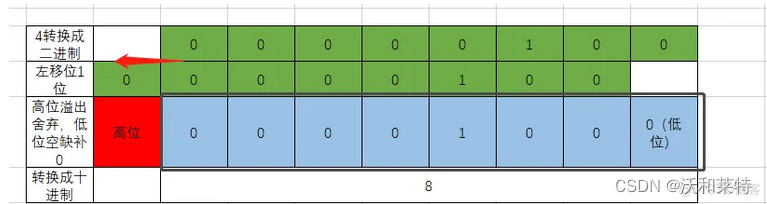
3:左移位运算符 <<
把’<<'左边的运算数的各二进制位全部左移若干位,<<右边的数字指定了向左移动的位数,高位溢出舍弃,低位补0;向左移动一位相当于*2
print(4 << 1) #8
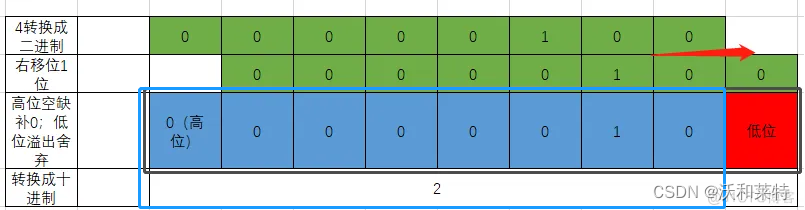
4:右移位运算符>>
把‘>>’左边的运算数的各二进制位全部右移若干位,>>右边的数字指定了向右移动的位数,低位溢出舍弃,高位补0;向右移动一位相当于/2
print(4>>1) #2
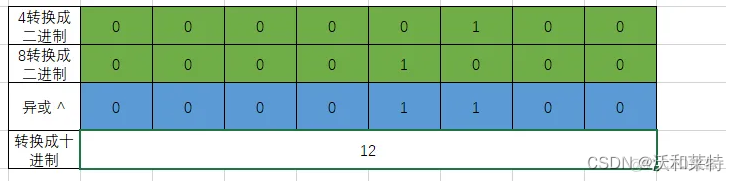
5:异或(^)
按位异或运算符,当两对应的二进位相异时,结果为1
print(4^8) #12
6:取反(~)
按位取反运算符:对数据的每个二进制位取反,即把1变为0,把0变为1
print(~5)#-6
取反过程
+5:
计算原码:0101
计算补码:0101(正数原码与补码相同)
对补码依次取反:1010(取反后数字的补码,由符号位可知为负数)
取反后数字反码:1001(负数的反码=补码-1)
取反后数字原码:1110(相对于反码符号位不变,数值位依次取反)
转化为十进制:-6
-4:
计算原码:1100
计算反码:1011(相对于原码符号位不变,数值位依次取反)
计算补码:1100(负数补码=反码+1)
对补码依次取反:0011(取反后数字的补码,由符号位可知为正数)
取反后数字原码:0011(正数原码、反码、补码相同)
转化为十进制:+3
我们可以直接记住取反的公式:
~x=-x-1
每篇一语
不忘初心,方得始终!
如有不足,感谢指正!
相关文章:

python学习——【第二弹】
前言 上一篇文章 python学习——【第一弹】给大家介绍了python中的基本数据类型等,这篇文章接着学习python中的运算符的相关内容。 运算符 python中的运算符主要有:算术运算符,赋值运算符,比较运算符,布尔运算符以及…...

242. 有效的字母异位词 349. 两个数组的交集
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 注意: 若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 示例 1: 输入: s “anagram”, t “nagaram” 输出: true 示例 2: 输入: s “rat…...

web网页设计——JavaScript一些语法
1、事件监听 语法: <1> 元素对象.addEventListener(‘事件类型’,要执行的函数) 三要素:(1)、事件源 (2)事件类型 (3)执行的函数 <2>元素对象.on事件类型 …...

php宝塔搭建部署实战CSM会议室预约系统源码
大家好啊,我是测评君,欢迎来到web测评。 本期给大家带来一套基于fastadmin开发的CSM会议室预约系统的源码。感兴趣的朋友可以自行下载学习。 技术架构 PHP7.2 nginx mysql5.7 JS CSS HTMLcnetos7以上 宝塔面板 文字搭建教程 下载源码࿰…...
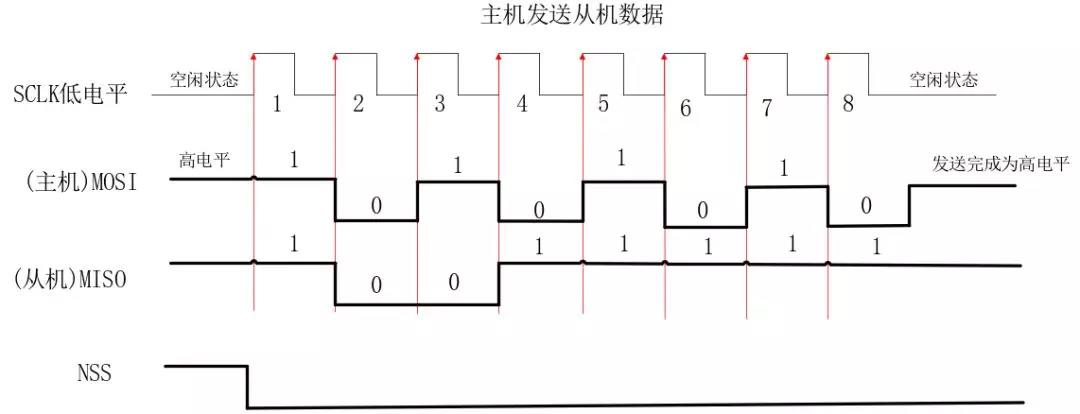
嵌入式知识点-SPI通讯
该文原自 : 正点原子 01 SPI概述 SPI (Serial Peripheralinterface),顾名思义就是串行外围设备接口。SPI是一种高速的,全双工,同步的通信总线,并且在芯片的管脚上只占用四根线,节约了芯片的管脚,同…...

C#教程--01 简介
简介 C# 是一个简单的、现代的、通用的、面向对象的编程语言,它是由微软(Microsoft)开发的。 C#的特性 现代的、通用的编程语言。 面向对象。 面向组件。 容易学习。 结构化语言。 它产生高效率的程序。 它可以在多种计算机平台上编译。 .Net 框架的一部分。 C#强大的编程…...
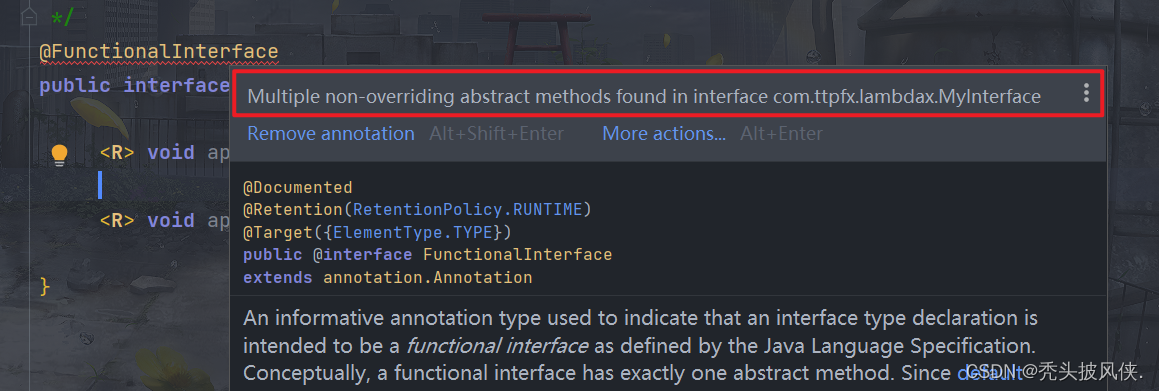
【java基础】一篇文章彻底搞懂lambda表达式
文章目录lambda表达式是什么lambda表达式的语法函数式接口初次使用深入理解方法引用 :: 用法快速入门不同形式的::情况1 object::instanceMethod情况2 Class::instanceMethod情况3 Class::staticMethod对于 :: 的一些示例及其注意事项构造器引用变量作用域使用外部变量定义内部…...
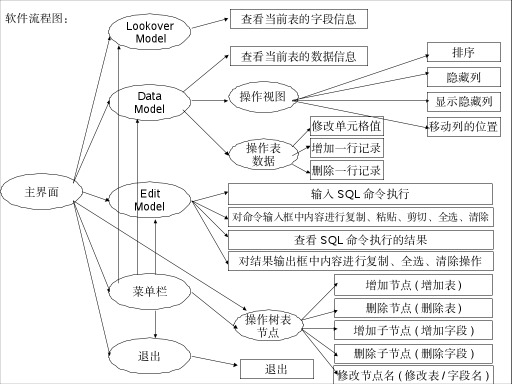
通用SQL查询分析器
技术:Java、JSP等摘要:本文主要针对当前很多软件都无法实现跨数据库、跨平台来执行sql语句而用户又仅需做一些基本的增删改查操作的矛盾,设计了一个能够跨平台跨数据库的软件。此软件是一个通用SQL查询分析器,利用java语言本身的跨…...
:038 朴素贝斯-处理离散数据)
机器学习100天(三十八):038 朴素贝斯-处理离散数据
《机器学习100天》完整目录:目录 机器学习100天,今天讲的是:朴素贝斯-处理离散数据! 打开 spyder,新建一个 naive_bayes_category.py 脚本。上一节我们引入了一批西瓜样本。并使用朴素贝叶斯公式计算出一个瓜蒂脱落、圆形、青色的西瓜是熟瓜的概率。下面我们来使用 pytho…...

【3.3】指针、二分、SSM项目
二分查找 class Solution {public int search(int[] nums, int target) {int n nums.length;int left 0;int right n - 1;while(left < right){int mid left (right - left) / 2;if(nums[mid] < target){left mid 1;}else if(nums[mid] > target){right mid …...

buu [INSHack2017]rsa16m 1
题目描述: 打开的 rsa_16m 文件 : (在此我只想说神人才找得到 c 的位置) ,这位置是真的难找啊 题目分析: 首先打开 description.md 文件,得到: 翻译下来: 当您需要真正…...
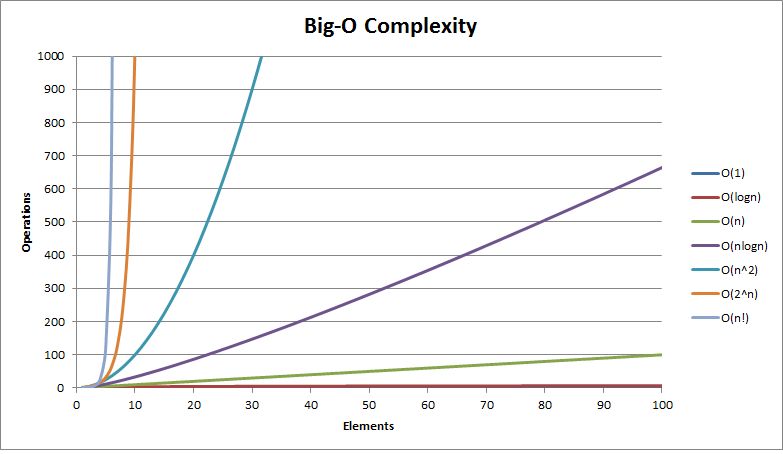
【数据结构起航】:衡量算法的好坏--时间空间复杂度
时间复杂度和空间复杂度 文章目录时间复杂度和空间复杂度1.算法效率1.1算法复杂度1.2复杂度在OJ里的应用2.时间复杂度2.1时间复杂度的概率2.2大O渐进表示法推导大O阶方法:2.3时间复杂度的举例计算3.空间复杂度3.1空间复杂度的举例计算4.复杂度各量级对比1.算法效率 …...

动手学深度学习【1】——线性回归
动手学深度学习网址:动手学深度学习 注:本部分只对基础知识进行简单的介绍并附上完整的代码实现,更多内容可参考上述网址。 简述 需要的准备知识 数学的偏导线性代数 线性模型 回归是能为一个或多个自变量与因变量之间关系建模的一类方…...

Html 相关知识
Html 相关知识 DOM 文档对象模型 (DOM) 是 HTML 和 XML 文档的编程接口。它提供了对文档的结构化的表述,并定义了一种方式可以使从程序中对该结构进行访问,从而改变文档的结构,样式和内容。DOM 将文档解析为一个由节点和对象(包…...

【冲刺蓝桥杯的最后30天】day1
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始逐渐恢复更新状态,正在备战蓝桥杯的小伙伴可以支持一下哦!…...

c++泛型编程与模板-01函数模板
函数模板的定义 所谓函数模板,实际就是写一个通用函数,返回值和参数的类型都是可变的,用一个特定格式的变量来指定,然后调用此函数的时候,编译器会根据参数的数据类型自动推导出类型,从而达到函数再不同的…...
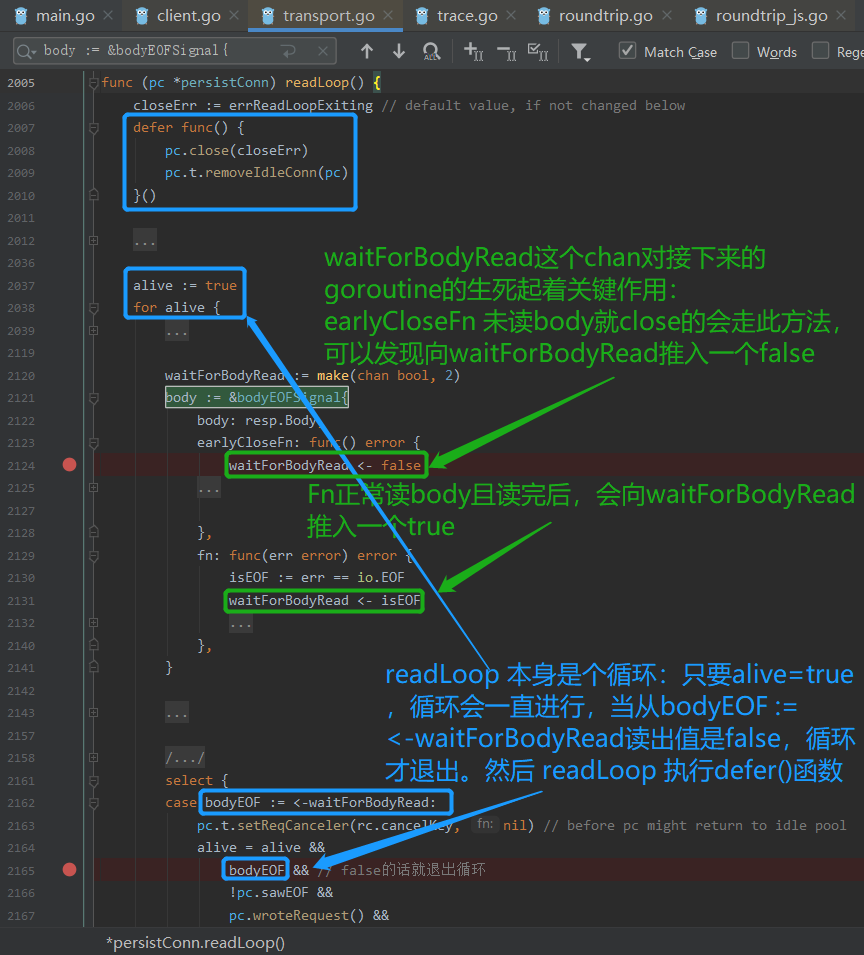
Golang http请求忘记调用resp.Body.Close()而导致的协程泄漏问题(含面试常见协程泄漏相关测试题)
参考: 知乎:别因为忘记close你的httpclient,造成goroutine泄漏 CSDN:resp.Body.Close() 引发的内存泄漏goroutine个数 先来看几道题,想一想最终的输出结果是多少呢? package mainimport ("fmt"…...

进程信号生命周期详解
信号和信号量半毛钱关系都没有! 每个信号都有一个编号和一个宏定义名称,这些宏定义可以在signal.h中找到,例如其中有定 义 #define SIGINT 2 查看信号的机制,如默认处理动作man 7 signal SIGINT的默认处理动作是终止进程,SIGQUIT的默认处理…...

2023-03-03干活小计
今天见识了 归一化的重要性:归一化 不容易爆炸 深度了解了学习率:其实很多操作 最后的结果都是改变了lr 以房价预测为例:一个点一个点更新 比较 矩阵的更新: 为什么小批量梯度下降 优于随机梯度下降 优于批量梯度下降ÿ…...

操作系统结构
随着操作系统的不断增多和代码规模的不断扩大,提供合理的结构对提升操作系统的安全与可靠性来说变得尤为重要。 1.分层法 指将操作系统分为若干层,最低层位硬件,最高层为用户接口,每层只能调用紧邻它的低层的功能和服务(类似于计…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
