力扣刷题-二叉树-合并二叉树
617.合并二叉树(经典)
合并二叉树是操作两棵树的题目里面很经典的,如何对两棵树遍历以及处理?
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:

注意: 合并必须从两个树的根节点开始。
思路
参考:https://programmercarl.com/0617.%E5%90%88%E5%B9%B6%E4%BA%8C%E5%8F%89%E6%A0%91.html
如何同时遍历两个二叉树呢?
其实和遍历一个树逻辑是一样的,只不过传入两个树的节点,同时操作。
递归
二叉树使用递归,就要想使用前中后哪种遍历方式?
本题使用哪种遍历都是可以的!
我们下面以前序遍历为例。
- 确定递归函数的参数和返回值:
首先要合入两个二叉树,那么参数至少是要传入两个二叉树的根节点,返回值就是合并之后二叉树的根节点。
- 因为是传入了两个树,那么就有两个树遍历的节点t1 和 t2,如果t1 == NULL 了,两个树合并就应该是 t2 了(如果t2也为NULL也无所谓,合并之后就是NULL)。
反过来如果t2 == NULL,那么两个数合并就是t1(如果t1也为NULL也无所谓,合并之后就是NULL)。
- 确定单层递归的逻辑:
单层递归的逻辑就比较好写了,这里我们重复利用一下t1这个树,t1就是合并之后树的根节点(就是修改了原来树的结构)。
那么单层递归中,就要把两棵树的元素加到一起。
接下来t1 的左子树是:合并 t1左子树 t2左子树之后的左子树。
t1 的右子树:是 合并 t1右子树 t2右子树之后的右子树。
最终t1就是合并之后的根节点。
class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution(object):def mergeTrees(self, root1, root2): # 传入参数 就是两棵树 这里以根节点表示""":type root1: TreeNode:type root2: TreeNode:rtype: TreeNode"""# 遍历两棵树 与遍历一棵树的逻辑是一样的 这里采用前序遍历的方式if not root1:return root2if not root2:return root1# 中 中的处理逻辑就是节点的值相加root1.val += root2.val # 根节点更新(以root1表示更新之后的树)# 左root1.left = self.mergeTrees(root1.left, root2.left)# 右root1.right = self.mergeTrees(root1.right, root2.right)return root1# 当然 也可以新建节点 比如 root迭代法
# 法二 迭代法 需要模拟队列来存储两棵树上的节点 这样就是层序遍历
from collections import deque
class Solution(object):def mergeTrees(self, root1, root2):if not root1:return root2if not root2:return root1queue = deque()queue.append(root1)queue.append(root2)while queue: # 以root1为更新之后的树# 弹出节点node1 = queue.popleft()node2 = queue.popleft()# 左if node1.left and node2.left: # 两边左节点都存在queue.append(node1.left)queue.append(node2.left)# 右if node1.right and node2.right: # 两边右节点都存在queue.append(node1.right)queue.append(node2.right)# 更新当前节点. 同时改变当前节点的左右孩子. node1.val += node2.valif not node1.left and node2.left: # node1无左节点 那就用node2的 node2没用也没事 就是Nullnode1.left = node2.leftif not node1.right and node2.right:node1.right = node2.rightreturn root1
相关文章:

力扣刷题-二叉树-合并二叉树
617.合并二叉树(经典) 合并二叉树是操作两棵树的题目里面很经典的,如何对两棵树遍历以及处理? 给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。 你需要将他们合并…...

了解JavaScript 加密、混淆和生成签名
分析并理解网站的 JavaScript 加密、混淆和生成签名的方法是 JavaScript 逆向工程中的一个重要方面。这些技术通常用于保护代码免遭未授权的访问和修改,或确保数据在传输过程中的安全性。 加密 目的:加密用于保护敏感数据,使得只有拥有正确密…...
)
Go语言的指针(深度解析)
指针是Go语言中的一个重要概念,它提供了对内存地址的直接访问和操作能力。通过指针,我们可以高效地传递和修改变量的值,避免了值传递所带来的拷贝开销。在本文中,我们将深入探讨Go语言指针的概念、使用方法和注意事项。 指针的本…...
HTB-SAU
信息收集 # cat port.nmap # Nmap 7.94 scan initiated Thu Jan 11 19:26:51 2024 as: nmap -sS --min-rate 10000 -p- -oN port.nmap 10.10.11.224 Nmap scan report for 10.10.11.224 (10.10.11.224) Host is up (0.28s latency). Not shown: 65531 closed tcp ports (r…...
AI创新之美:AIGC探讨2024年春晚吉祥物龙辰辰的AI绘画之独特观点
🎬 鸽芷咕:个人主页 🔥 个人专栏:《粉丝福利》 《linux深造日志》 ⛺️生活的理想,就是为了理想的生活! ⛳️ 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下…...

Linux的SSH服务
一.SSH服务简介 1.什么是SSH SSH(Secure Shell)是一种安全通道协议,主要用来实现字符界面的远程登录、远程复制等功能。SSH 协议对通信双方的数据传输进行了加密处理,其中包括用户登录时输入的用户口令,SSH 为建立在应…...

MySQL连续案例续集
01)查询学过「张三」老师授课的同学的信息 SELECT s.*, c.cname, t.tname, sc.score FROM t_mysql_teacher t, t_mysql_course c, t_mysql_student s, t_mysql_score sc WHERE t.tid c.tid AND c.cid sc.cid AND sc.sid s.sid AND t.tname ‘张三’ 02&#x…...

【STM32读取HX711的函数】
[两个普通IO读取HX711数据的函数-主芯片是STM32F407] 以下是.h文件中的内容: #ifndef __hx711_h #define __hx711_h #define HX711CH1_DIO_GROUP GPIOA #define HX711CH1_CLK_GROUP GPIOA #define HX711CH1_DIO_PIN GPIO_Pin_1 #define HX711CH1_CLK_PIN GPIO_Pin…...

MATLAB对数据隔位抽取和插值的几种方法
对于串行的数据,有时我们需要转成多路并行的数据进行处理,抽取;或者是需要对数据进行隔点抽取,或对数据进行插值处理。此处以4倍抽取或插值为例,MATLAB代码实现。 文章目录 抽取方法一:downsample函数方法…...
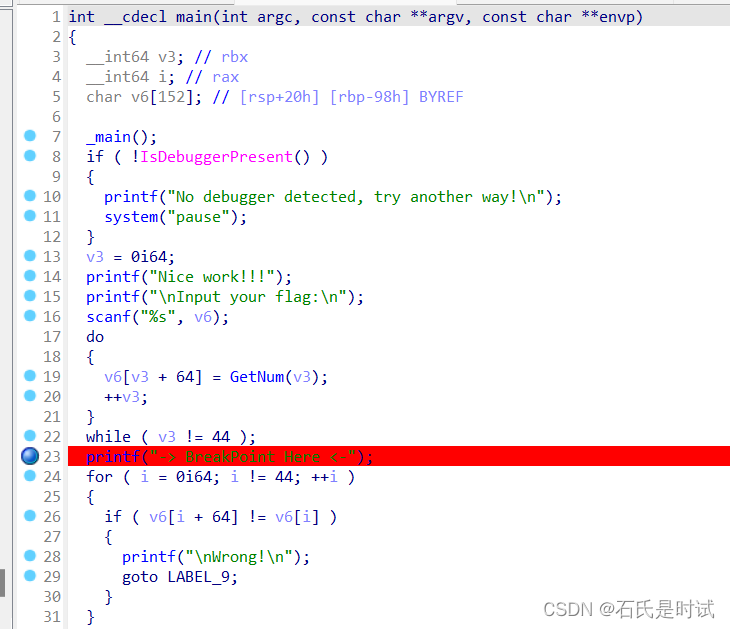
[NSSCTF Round#16 Basic] CPR
打着玩玩,比赛很简单。 Crypto pr 一个RSA题,n1p*q,n2q*r给了两个c和p,r而且flag经过pad用单因子无法解出。分别用p,r解完再取crt from Crypto.Util.number import * import randomflagplaintext NSSCTF{****************} charset abcdefghijklmn…...

LAMMPS 文献:9 种熔化温度模拟方法的总结与比较:两相法、单相法以及缺陷法
记录一下检索到一篇通过LAMMPS模拟熔化温度的总结文章:单相方法、过热–过冷方法、Z 方法、修正 Z 方法、孔洞方法、修正孔洞方法、两相方法、夹层方法以及修正两相法。 感谢论文的原作者! 文章题目: A comprehensive investigation on the…...
)
JSR-107 (JCACHE)
JSR107 Specification 1.1.1 Maintenance Release https://docs.google.com/document/d/1ijduF_tmHvBaUS7VBBU2ZN8_eEBiFaXXg9OI0_ZxCrA/edit?pli1 What is JSR-107? JSR-107 is a standardized API for temporary, in-memory caching in Java applications. It defines a s…...

kylin4.0.3升级问题
话接前文: kylin升级(3.0.1->kylin-4.0.3)-CSDN博客文章浏览阅读941次,点赞29次,收藏12次。原本的cube太多了,换其他OLAP数据库太麻烦。相比之下,升级是一个很好的选择(官网有说明内存降低和构…...
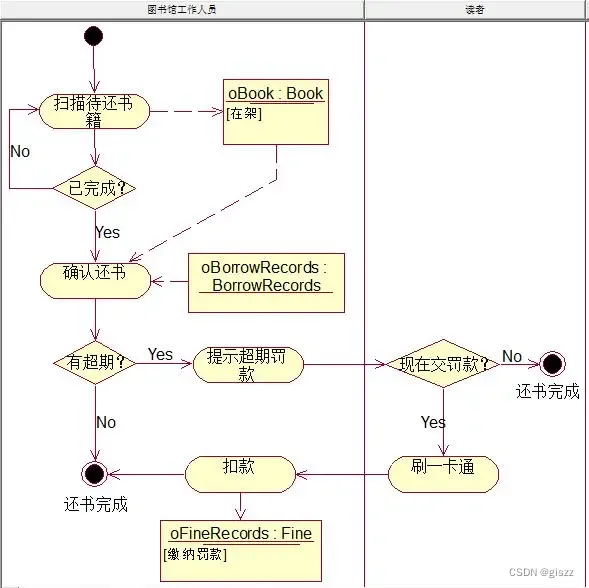
【UML】第16篇 活动图
目录 一、什么是活动图 二、应用场景: 三、绘图符号的说明: 四、语法: 五、例图 六、建模的流程 6.1 对业务流程建模时 6.2 对用例进行活动图建模时 一、什么是活动图 活动图(Activity Diagram)是UML中用于描…...

Python学习之路-函数进阶
Python学习之路-函数进阶 参数和返回值的作用 函数根据有没有参数以及有没有返回值,可以相互组合,一共有4 种组合形式:无参数,无返回值;无参数,有返回值;有参数,无返回值ÿ…...
Mac打包Unix可执行文件为pkg
Mac打包Unix可执行文件为pkg 方式一:通过packages页面打包 1.下载packages app Distribution:自定义化更高,包括修改安装页面的内容提示 我这里主要演示Distribution模式的项目:通过unix可执行文件postinstall.sh脚本实现通过ma…...
)
C++ 模拟散列表 || 哈希表存储与查询,模版题(拉链法)
维护一个集合,支持如下几种操作: I x,插入一个整数 x ; Q x,询问整数 x 是否在集合中出现过; 现在要进行 N 次操作,对于每个询问操作输出对应的结果。 输入格式 第一行包含整数 N ,…...
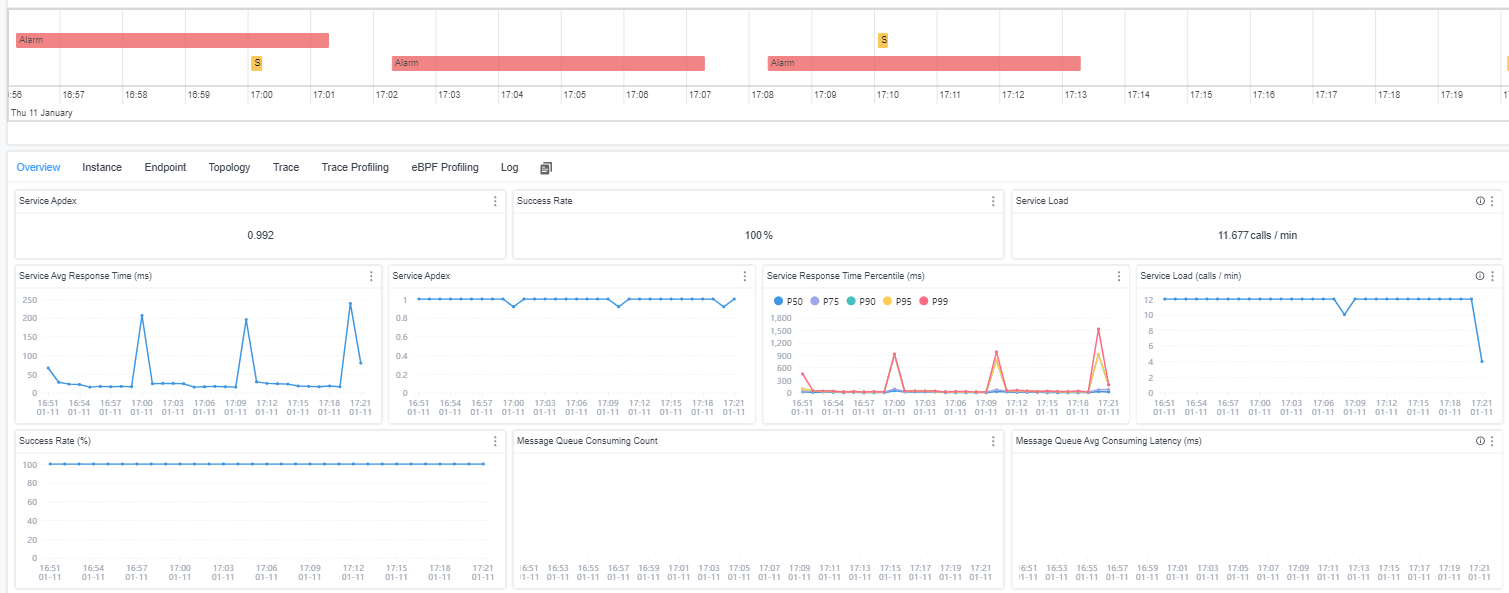
详解Skywalking 服务Overview页面的参数含义(适合小白)
本文针对刚刚接触skywalking的同学,重点讲解服务Overview页面中各个参数的含义,为大家快速上手skywalking会起到帮助作用! 最重要的三个指标 Service Apdex(数字):当前服务的评分 Successful Rate(数字&a…...

Android studio GridView应用设计
一、xml布局文件设计: <GridViewandroid:id="@+id/gridView"android:layout_width="match_parent"android:layout_height="match_parent"tools:layout_editor_absoluteX="1dp"tools:layout_editor_absoluteY="1dp"andr…...
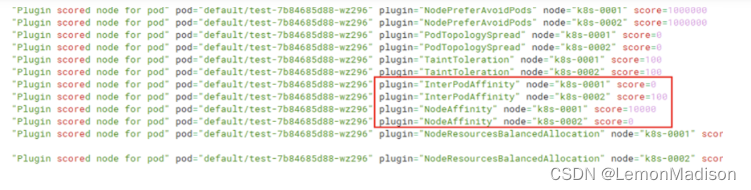
K8s 是如何完成调度和权重调整?
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、调度流程二、kuble-scheduler 调度原理1 kubernetes 1.23版本调度器filter阶段和score阶段源码分析2 修改调度器插件默认权重示例2.1 环境准备2.2 调整Inte…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
