力扣(105. 从前序与中序遍历序列构造二叉树,106. 从中序与后序遍历序列构造二叉树)
题目1链接
题目1:
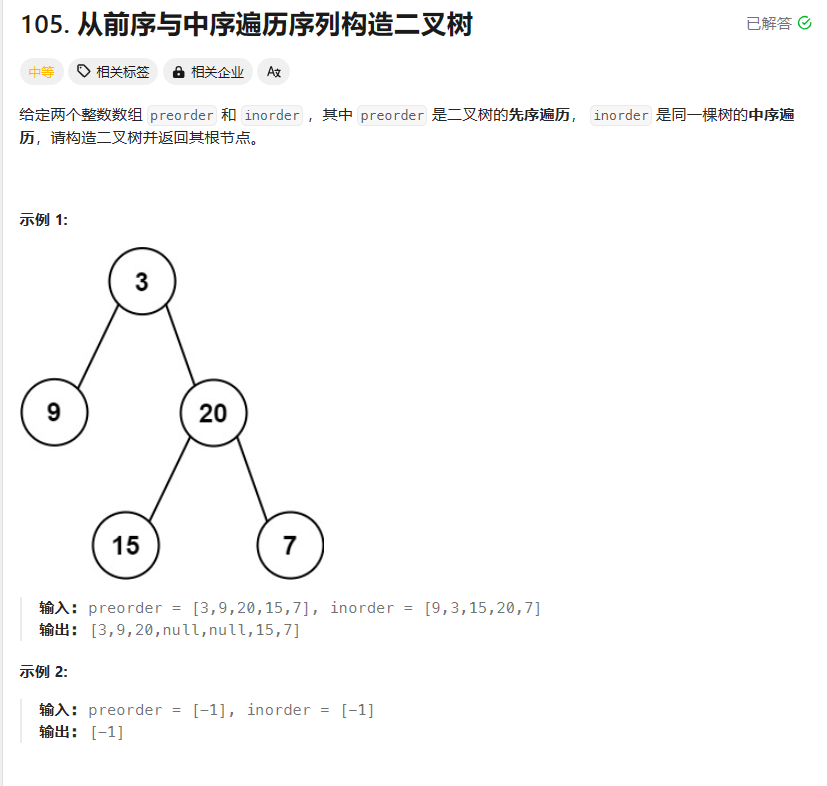
思路:使用前序确定根,使用中序分左右子树,分治法。
难点:如何控制递归确定左右子树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*///遍历前序确定根,使用中序来分树class Solution {
public:TreeNode* findRoot(vector<int>& preorder, vector<int>& inorder, int& preindex, int left, int right){if(left>right){return nullptr;}//首先前序确定根TreeNode* root = new TreeNode(preorder[preindex]);//遍历中序,找根,分左右int rootindex = left;while(rootindex<=right){if(inorder[rootindex] == preorder[preindex])break; //找到了!rootindex++;}preindex++;// [left, rootindex-1] rootindex [rootindex+1, right]root->left = findRoot(preorder, inorder, preindex, left, rootindex-1);root->right = findRoot(preorder, inorder, preindex, rootindex+1, right);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i = 0;return findRoot(preorder, inorder, i,0, inorder.size()-1);}
};
题目2链接
题目2:

题目1会了,题目二就一定会了!
注意:后序(左右根)从后往前确定根,中序分左右子树。
递归时,先遍历右子树,再遍历左子树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* findRoot(vector<int>& inorder, vector<int>& postorder, int& postindex, int left, int right){if(left>right){return nullptr;}//首先后序确定根TreeNode* root = new TreeNode(postorder[postindex]);//遍历中序,找根,分左右int rootindex = left;while(rootindex<=right){if(inorder[rootindex] == postorder[postindex])break; //找到了!rootindex++;}postindex--;// [left, rootindex-1] rootindex [rootindex+1, right]root->right = findRoot(inorder, postorder, postindex, rootindex+1, right);root->left = findRoot(inorder, postorder, postindex, left, rootindex-1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int i = postorder.size() - 1;return findRoot(inorder, postorder, i, 0, inorder.size()-1);}
};
相关文章:

力扣(105. 从前序与中序遍历序列构造二叉树,106. 从中序与后序遍历序列构造二叉树)
题目1链接 题目1: 思路:使用前序确定根,使用中序分左右子树,分治法。 难点:如何控制递归确定左右子树。 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* T…...
网络安全技术新手入门:在docker上安装dvwa靶场
前言 准备工作:1.已经安装好kali linux 步骤总览:1.安装好docker 2.拖取镜像,安装dvwa 一、安装docker 输入命令:sudo su 输入命令:curl -fsSL https://download.docker.com/linux/debian/gpg | sudo apt-key …...
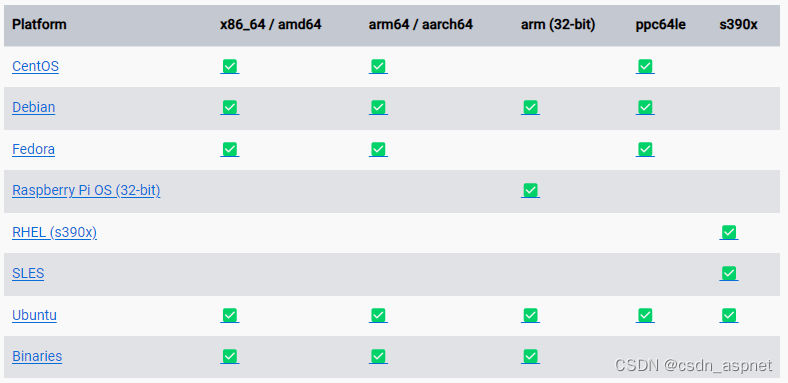
Docker 介绍 及 支持的操作系统
Docker组成: Docker主机(Host): 一个物理机或虚拟机, 用于运行Docker服务进程和容器, 也成为宿主机, node节点。 Docker服务器端(Server): Docker守护进程, 运行Docker容器。 Docker客户端(Client): 客户端使用docker命令或其他工…...

大模型实战营Day5 LMDeploy大模型量化部署实践
模型部署 定义 产品形态 计算设备 大模型特点 内存开销大 动态shape 结构简单 部署挑战 设备存储 推理速度 服务质量 部署方案:技术点 (模型并行 transformer计算和访存优化 低比特量化 Continuous Batch Page Attention)方案(…...
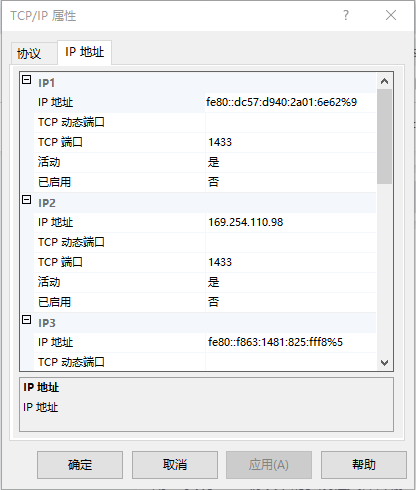
py连接sqlserver数据库报错问题处理。20009
报错 pymssql模块连接sqlserver出现如下错误: pymssql._pymssql.OperationalError) (20009, bDB-Lib error message 20009, severity 9:\nUnable to connect: Adaptive Server is unavailable or does not exist (passwordlocalhost)\n) 解决办法: 打…...

LTESniffer:一款功能强大的LTE上下行链路安全监控工具
关于LTESniffer LTESniffer是一款功能强大的LTE上下行链路安全监控工具,该工具是一款针对LTE的安全开源工具。 该工具首先可以解码物理下行控制信道(PDCCH)并获取所有活动用户的下行链路控制信息(DCI)和无线网络临时…...
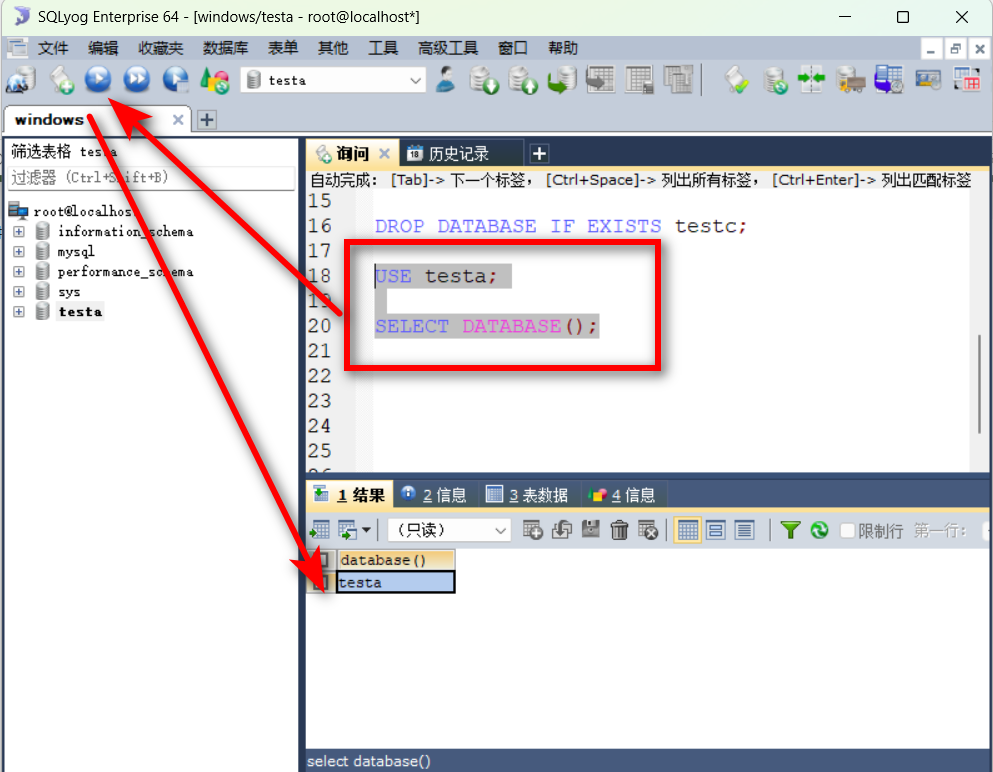
SQL语句详解二-DDL(数据定义语言)
文章目录 操作数据库创建:Create查询:Retrieve修改:Update删除:Delete使用数据库 操作表常见的几种数据类型创建:Create复制表 查询:Retrieve修改:Update删除:Delete 操作数据库 创…...
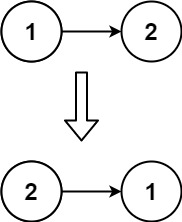
web前端算法简介之链表
链表 链表 VS 数组链表类型链表基本操作 创建链表:插入操作:删除操作:查找操作:显示/打印链表:反转链表:合并两个有序链表:链表基本操作示例 JavaScript中,instanceof环形链表 判断…...

C++函数对象
任何定义了函数调用操作符的对象都是函数对象。C 支持创建、操作新的函数对象,同时也提供了许多内置的函数对象。 函数包装器 std::function 提供存储任意类型函数对象的支持。 function (C11) 包装具有指定函数调用签名的任意类型的可调用对象 (类模板) bad_funct…...

插件化简单介绍
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、商业变现、人工智能等,希望大家多多支持。 未经允许不得转载 目录 一、导读二、概览三、常见的插件化方案…...
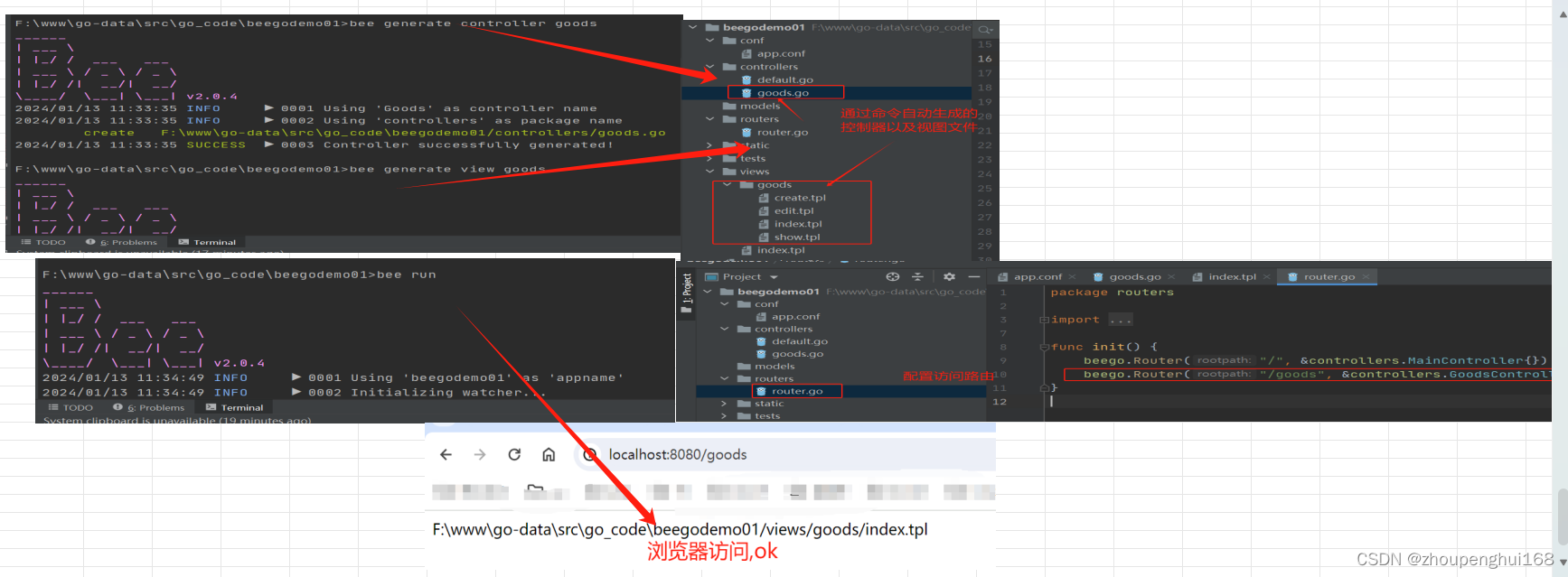
[Beego]1.Beego简介以及beego环境搭建,bee脚手架的使用,创建,运行项目
一.Beego介绍 Beego是一个开源的基于Golang的MVC框架,主要用于Golang Web开发,Beego可以用来快速开发API、Web、后端服务等各种应用。 Golang 的Web开发框架有很多,从 github star 数量来看Gin>Beego>lris>Echo>Revel>Buffalo 目前国内用的比较多的就…...
)
Tomcat 静态资源访问与项目根路径设置(AI问答)
一个静态文件,放在Tomcat中,希望能够通过网络访问,应该放在哪里? 在Apache Tomcat中,如果想要部署静态文件(例如HTML、CSS、JavaScript、图片等)并能通过网络访问,通常需要将这些文…...

Docker实战09|使用AUFS包装busybox
前几篇文章中,重点讲解了如何实现构建容器,需要回顾的小伙伴可以看以下文章: 《Docker实战06|深入剖析Docker Run命令》《Docker实战07|Docker增加容器资源限制》《Docker实战08|Docker管道及环境变量识别…...
?如何使用它?)
什么是uni.request()?如何使用它?
uni.request()是uni-app提供的一个用于发起网络请求的API。 使用uni.request()的步骤如下: 在需要发起网络请求的页面中引入uni.request()方法。 调用uni.request()方法,并传入相应的参数,包括请求地址、请求方法、请求头部和请求数据等。 …...

用React给XXL-JOB开发一个新皮肤(一):环境搭建和项目初始化
目录 一. 简述二. Fork 项目三. 搭建开发环境四. 初始化皮肤项目五. 添加相关依赖六. 预览 一. 简述 大名鼎鼎的 xxl-job 任务调度中心我们应该都使用过,项目地址:xxl-job。它是一个分布式任务调度平台,其核心设计目标是开发迅速、学习简单…...
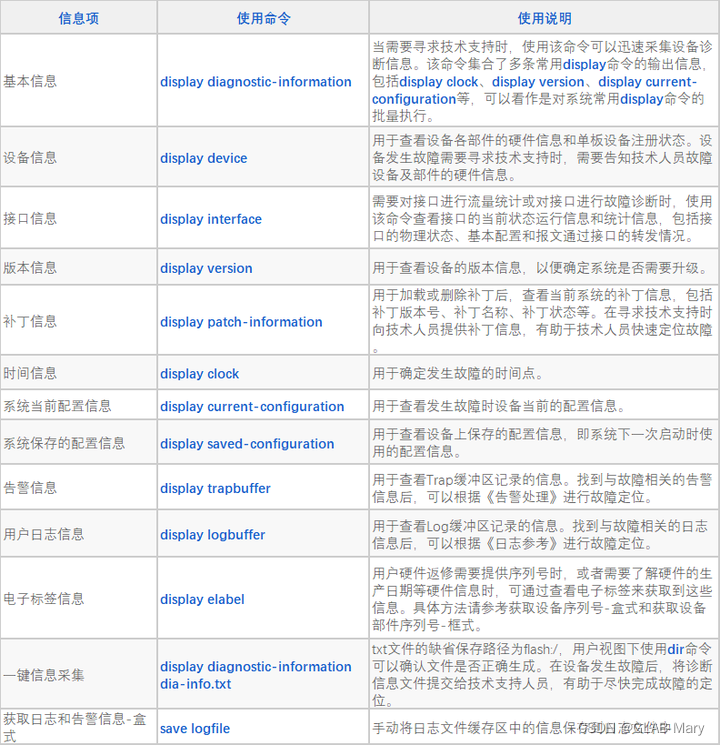
华为常用的命令——display,记得点赞收藏!
华为设备提供了多条display命令用于查看硬件部件、接口及软件的状态信息。通常这些状态信息可以为用户故障处理提供定位思路。 常用的故障信息搜集的命令如下: 路由器常用维护命令表 交换机常用的故障信息搜集 关注 工 仲 好:IT运维大本营,获…...

Costco攻入山姆大本营
01 Costco深圳店开业火爆 “我今天不去Costco,早上还没开业,路上就已经堵车了,看来今天人很多,过几天再去”,原本计划在Costco开业当天去逛逛的张芸(化名)无奈只能放弃。 家住在Costco深圳店旁…...

什么是常量?如何区分常量和变量?
一、问题 什么是常量,什么是变量?怎样区分⼆者? 二、解答 1. 常量与变量 (1)常量即其值在程序运⾏的过程中是不可以改变的,如123,-4567 为数值常量; (2)变量…...

uniapp返回上一页并刷新数据
在uniapp中,返回页面时onLoad是不会触发的 如果只需要在特定情况下返回上一页才需要刷新数据 可以使用$emit和$no去解决 例如:注册完成后返回到首页并隐藏注册按钮,register.vue和index.vue register.vue <template><view clic…...
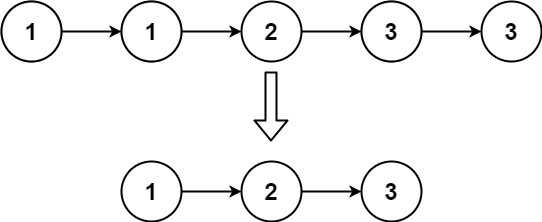
LeetCode 0083.删除排序链表中的重复元素:模拟
【LetMeFly】83.删除排序链表中的重复元素:模拟 力扣题目链接:https://leetcode.cn/problems/remove-duplicates-from-sorted-list/ 给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
