视觉SLAM十四讲|【五】相机与IMU时间戳同步
视觉SLAM十四讲|【五】相机与IMU时间戳同步
相机成像方程
Z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] = K P Z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix}= KP Z uv1 = fx000fy0cxcy1 XYZ =KP
其中,
K = [ f x 0 c x 0 f y c y 0 0 1 ] K=\begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} K= fx000fy0cxcy1
时间戳同步
假设视觉特征在图像平面上匀速移动,则特征在相机成像平面上的运动速度为
V l k = ( [ u l k + 1 v l k + 1 ] − [ u l k v l k ] ) / ( t k + 1 − t k ) V_l^k =( \begin{bmatrix} u_l^{k+1} \\ v_l^{k+1} \end{bmatrix} - \begin{bmatrix} u_l^{k} \\ v_l^{k} \end{bmatrix})/(t_{k+1}-t_k) Vlk=([ulk+1vlk+1]−[ulkvlk])/(tk+1−tk)
设世界坐标系中 l l l个地图点坐标为
f l w = [ x , y , z ] T f_l^w = [x, y,z]^T flw=[x,y,z]T
变换到相机坐标系下则为
f l c i = R c b R w b i T ( f l w − p w b i ) + p c b f_l^{c_i} = R_{cb}R_{wb_i}^T(f_l^w - p_{wb_i}) + p_{cb} flci=RcbRwbiT(flw−pwbi)+pcb再投影到图像平面,并计算重投影残差
r c = [ x l i z l i − u l i , y l i z l i − v l i ] T r_c = [\frac{x_l^i}{z_l^i}-u_l^i, \frac{y_l^i}{z_l^i}-v_l^i]^T rc=[zlixli−uli,zliyli−vli]T
考虑时间延迟对特征坐标的补偿为
z l i ( t d ) = [ u l i , v l i ] T + t d v l i z_l^i(t_d) = [u_l^i, v_l^i]^T + t_d v_l^i zli(td)=[uli,vli]T+tdvli
逆深度参数化方式
SLAM中特征点的参数化表示有很多,最直接的是用三维坐标XYZ来表示,但通常大家更喜欢用逆深度表示,因为逆深度优势在于能够建模无穷远点。回顾相机成像方程
Z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] = K P Z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix}= \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix}= KP Z uv1 = fx000fy0cxcy1 XYZ =KP
有
P = 1 λ K − 1 [ u v 1 ] P=\frac{1}{\lambda}K^{-1} \begin{bmatrix}u \\v \\ 1 \end{bmatrix} P=λ1K−1 uv1
对于世界坐标系中的某相机观测点 f l c i f_l^{c_i} flci,可以用相机逆深度成像公式得到,如下所示
f l c i = 1 λ K − 1 [ u l i v l i 1 ] f_l^{c_i}=\frac{1}{\lambda}K^{-1} \begin{bmatrix}u_l^i \\v_l^i \\ 1 \end{bmatrix} flci=λ1K−1 ulivli1
考虑到坐标系转换关系
f l w = R w c i f l c i + p w c i f_l^w = R_{wc_i}f_l^{c_i}+p_{wc_i} flw=Rwciflci+pwci
观测点 f l c i f_l^{c_i} flci也可以通过运动姿态进行推测,有
f l c i ~ = R c i w f l w + p c i w \tilde{{f_l^{c_i}}} = R_{c_iw}f_l^w+p_{c_iw} flci~=Rciwflw+pciw
我们研究的是投影面内的残差,因此,不考虑时间延迟的残差可以写为如下形式
r c 3 = [ u l j v l j 1 ] − λ K f l c j ~ r_{c3} = \begin{bmatrix} u_l^j\\ v_l^j \\1 \end{bmatrix} - \lambda K \tilde{{f_l^{c_j}}} rc3= uljvlj1 −λKflcj~
r c 3 = [ u l j v l j 1 ] − λ K ( R c j w f l w + p c j w ) r_{c3} = \begin{bmatrix} u_l^j\\ v_l^j \\1 \end{bmatrix} - \lambda K(R_{c_jw}f_l^w + p_{c_jw}) rc3= uljvlj1 −λK(Rcjwflw+pcjw)
r c 3 = [ u l j v l j 1 ] − λ K ( R c j w ( R w c i f l c i + p w c i ) + p c j w ) r_{c3} = \begin{bmatrix} u_l^j\\ v_l^j \\1 \end{bmatrix} - \lambda K(R_{c_jw}(R_{w c_i}f_l^{c_i}+p_{wc_i})+ p_{c_jw}) rc3= uljvlj1 −λK(Rcjw(Rwciflci+pwci)+pcjw)
又因为
f l c i = 1 λ K − 1 [ u l i v l i 1 ] f_l^{c_i}=\frac{1}{\lambda}K^{-1} \begin{bmatrix}u_l^i \\v_l^i \\ 1 \end{bmatrix} flci=λ1K−1 ulivli1
r c 3 = [ u l j v l j 1 ] − λ K ( R c j w ( R w c i ( 1 λ K − 1 [ u l i v l i 1 ] ) + p w c i ) + p c j w ) r_{c3} = \begin{bmatrix} u_l^j\\ v_l^j \\1 \end{bmatrix} - \lambda K(R_{c_jw}(R_{w c_i}(\frac{1}{\lambda}K^{-1} \begin{bmatrix}u_l^i \\v_l^i \\ 1 \end{bmatrix})+p_{wc_i})+ p_{c_jw}) rc3= uljvlj1 −λK(Rcjw(Rwci(λ1K−1 ulivli1 )+pwci)+pcjw)
[ u l j v l j ] = [ 1 0 0 0 1 0 ] [ u l j v l j 1 ] \begin{bmatrix} u_l^j\\ v_l^j \end{bmatrix} = \begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} u_l^j\\ v_l^j \\1 \end{bmatrix} [uljvlj]=[100100] uljvlj1
令
C = [ 1 0 0 0 1 0 ] C = \begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \end{bmatrix} C=[100100]
有
r c = C r c 3 r_c = C r_{c3} rc=Crc3
r c = C [ u l j v l j 1 ] − λ C K ( R c j w ( R w c i ( 1 λ K − 1 [ u l i v l i 1 ] ) + p w c i ) + p c j w ) r_{c} = C\begin{bmatrix} u_l^j\\ v_l^j \\1 \end{bmatrix} - \lambda CK(R_{c_jw}(R_{w c_i}(\frac{1}{\lambda}K^{-1} \begin{bmatrix}u_l^i \\v_l^i \\ 1 \end{bmatrix})+p_{wc_i})+ p_{c_jw}) rc=C uljvlj1 −λCK(Rcjw(Rwci(λ1K−1 ulivli1 )+pwci)+pcjw)
现在考虑时间延迟
r c = C ( [ u l j v l j 1 ] + v j t d ) − λ C K ( R c j w ( R w c i ( 1 λ K − 1 [ u l i v l i 1 ] ) + p w c i ) + p c j w ) r_{c} = C(\begin{bmatrix} u_l^j\\ v_l^j \\1 \end{bmatrix} + v_jt_d) - \lambda CK(R_{c_jw}(R_{w c_i}(\frac{1}{\lambda}K^{-1} \begin{bmatrix}u_l^i \\v_l^i \\ 1 \end{bmatrix})+p_{wc_i})+ p_{c_jw}) rc=C( uljvlj1 +vjtd)−λCK(Rcjw(Rwci(λ1K−1 ulivli1 )+pwci)+pcjw)
其中
v j = ( [ u k + 1 v k + 1 1 ] − [ u k v k 1 ] ) / ( t k + 1 − t k ) v_j =(\begin{bmatrix} u_{k+1} \\ v_{k+1} \\ 1\end{bmatrix} - \begin{bmatrix} u_{k} \\ v_{k} \\ 1\end{bmatrix})/(t_{k+1}-t_k) vj=( uk+1vk+11 − ukvk1 )/(tk+1−tk)
相关文章:

视觉SLAM十四讲|【五】相机与IMU时间戳同步
视觉SLAM十四讲|【五】相机与IMU时间戳同步 相机成像方程 Z [ u v 1 ] [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] K P Z \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \…...

js null和undefined的区别
null和undefined在JavaScript中都表示“无”的概念,但它们在使用和含义上有一些重要的区别。 含义: null 是一个表示“无”的对象,当转换为数值时结果为0。 undefined 是一个表示“缺少值”的原始值,当转换为数值时结果为NaN。…...

Arduino| IDE下载、安装和设置以及开发板的连接
IDE下载、安装和设置以及开发板的连接 IDE下载IDE安装IDE设置首选项——设置语言、字体、主题、地址等等开发板管理器——添加开发板 开发板的连接 IDE下载 第一步:进入Arduino官网https://www.arduino.cc。 第二步:选择导航栏的Software,然…...
Linux之Ubuntu环境Jenkins部署前端项目
今天分享Ubuntu环境Jenkins部署前端vue项目 一、插件安装 1、前端项目依赖nodejs,需要安装相关插件 点击插件管理,输入node模糊查询 选择NodeJS安装 安装成功 2、配置nodejs 点击后进入 点击新增 NodeJS 配置脚手架类型:如果不填 默认npm …...

QT下的几种实现modbus的库,记录
QModbus QT提供了一个名为QModbus的模块,可以实现Modbus的主机或从机功能 pro需要添加 QT += serialbus serialport相关头文件 #include <QModbusTcpClient> #include <QModbusDataUnit> 具体使用参考: https://blog.csdn.net/XCJandLL/article/details/1…...
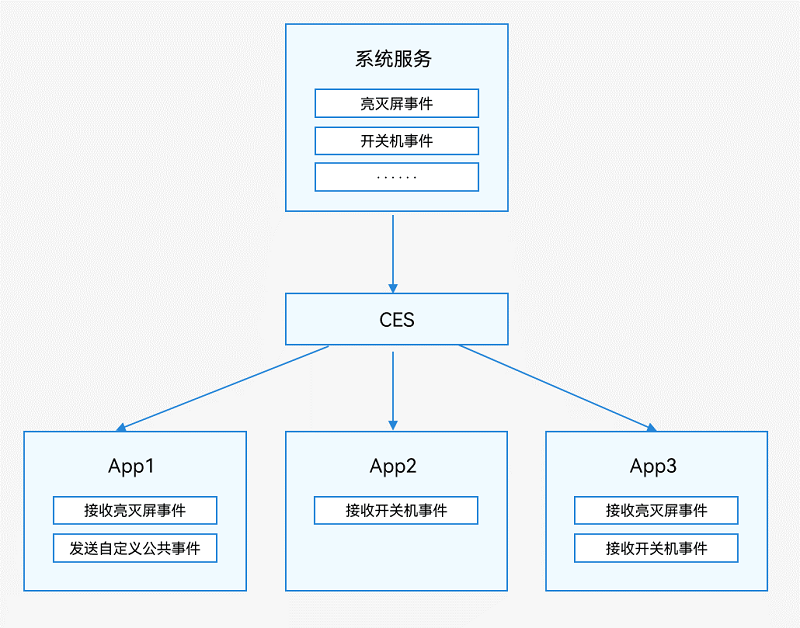
HarmonyOS4.0系统性深入开发18公共事件简介
公共事件简介 HarmonyOS通过CES(Common Event Service,公共事件服务)为应用程序提供订阅、发布、退订公共事件的能力。 公共事件从系统角度可分为:系统公共事件和自定义公共事件。 系统公共事件:CES内部定义的公共事…...
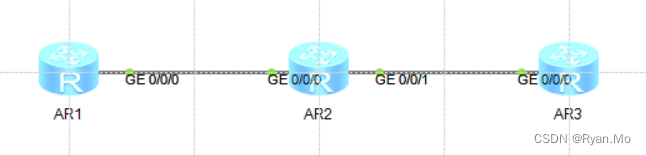
华为路由器OSPF动态链路路由协议配置
R1配置 interface GigabitEthernet0/0/0ip address 10.1.12.1 255.255.255.252 interface LoopBack0ip address 1.1.1.1 255.255.255.255 ospf 1 router-id 1.1.1.1 area 0.0.0.0 network 1.1.1.1 0.0.0.0 network 10.1.12.0 0.0.0.3 R2配置 interface GigabitEthernet0/0/0i…...
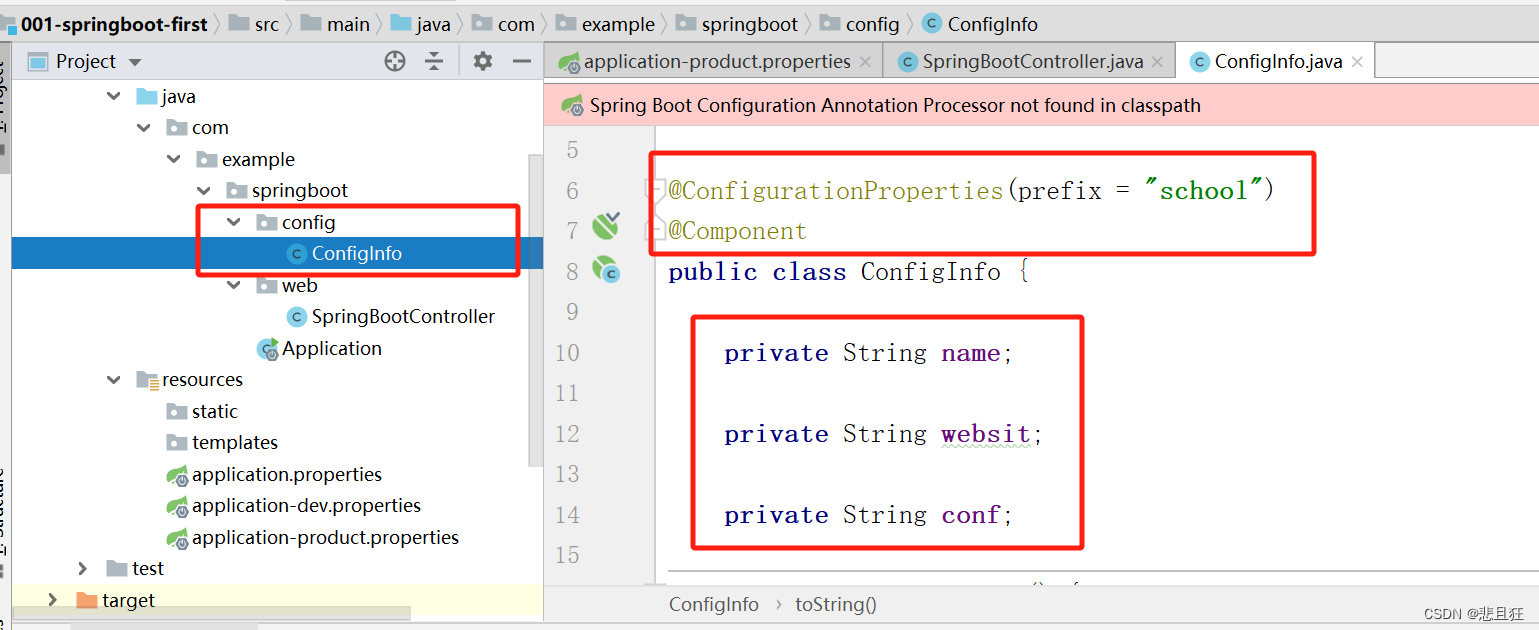
常用注解/代码解释(仅个人使用)
目录 第一章、代码解释①trim() 方法以及(Arrays.asList(str.split(reg)));②查询字典项②构建后端镜像shell命令解释 第二章、注解解释①PropertySource注解与Configurationproperties注解的区别 第三章、小知识①Linux系统中使用$符号表示变量 友情提醒: 先看文章目录&#…...
2024阿里云服务器ECS介绍_全方位解析_CPU性能详解
阿里云服务器ECS英文全程Elastic Compute Service,云服务器ECS是一种安全可靠、弹性可伸缩的云计算服务,阿里云提供多种云服务器ECS实例规格,如经济型e实例、通用算力型u1、ECS计算型c7、通用型g7、GPU实例等,阿里云百科aliyunbai…...

向伟人学习反焦虑,在逆境中崛起
第一、乐观的精神。 伟人在长期以来的读书、思考和实践,突破了思想认知限制,并最终在更高的思维层面上,建立起了强大的精神信念感。 在危险环境中表示绝望的人, 在黑暗中看不见光明的人, 只是懦夫与机会主义者。 —— …...
线上问题整理
JVM 案例 案例一:服务器内存不足,影响Java应用 问题: 收到报警,某Java应用集群中一台服务器可用内存不足,超过报警阈值。 排查过程: 首先,通过Hickwall查看该应用各项指标,发现无论…...

【elastic search】详解elastic search集群
目录 1.与集群有关的一些概念 2.集群搭建 3.集群搭建 4.kibana链接集群 5.选举流程 6.请求流程 7.master的作用 1.与集群有关的一些概念 数据分片: 数据分片(shard),单台服务器的存储容量是有限的,把一份数据…...

近红外光谱分析技术与基于深度学习的化学计量学方法
郁磊【副教授】:主要从事AI人工智能与大数据分析等相关研究,长期致力于人工智能与近红外生物医学工程等领域融合,主持并完成多项科研课题。著有《神经网络43个案例分析》等书籍。 // 讲座内容 1、近红外光谱基本理论、近红外光谱仪基本原理…...
Elasticsearch windows开箱即用【记录】
一、准备工作 安装ES之前要在本机安装好JDK,对应的兼容性见官网链接:https://www.elastic.co/cn/support/matrix ES官网链接:https://www.elastic.co/cn/, 我本机安装的是JDK8,测试使用的是7.3.0版本的ES和Kibana。 1、首先去…...

第 3 课 ROS 常用术语及命令说明
1.ROS文件系统的组成 ROS 文件是由 Packages 和 Manifests ( package.xml )组成。 Packages:功能包,是 ROS 软件中的基本单元,包含节点源码、配置文件、数据定义等。 Manifest( package xml &#x…...

基于AidLux的智慧教育版面分析应用
基于AidLux的智慧教育版面分析应用 1. Aidlux平台介绍 融合架构操作系统AidLux,可以为单一ARM设备同时提供Android和Linux运行环境,双系统既能独立使用又能相互通信。 非虚拟机方式实现双系统融合并行 同时拥有两个系统的完整用户体验无需重启即可在两个系统之间…...

Spring | Spring框架最基本核心的jar包、Spring的入门程序、依赖注入
目录: 1.Spring框架最基本、最核心的jar包2.Spring的入门程序3.依赖注入3.1 依赖注入的概念3.2 依赖注入的实现方式 1.Spring框架最基本、最核心的jar包 Spring是一个轻量级框架,Spring最基本、最核心的的jar包括 : beans、context、core、expression。 …...
--大模型相关、扩散模型、视觉导航)
[晓理紫]每日论文推送(有中文摘要,源码或项目地址)--大模型相关、扩散模型、视觉导航
专属领域论文订阅 VX关注{晓理紫|小李子},每日更新论文,如感兴趣,请转发给有需要的同学,谢谢支持 分类: 大语言模型LLM视觉模型VLM扩散模型视觉导航具身智能,机器人强化学习开放词汇,检测分割 LLM 标题:…...

【软件项目管理_软件工程】软件项目管理课后相关习题
(1)需求分析是回答系统必须(A)的问题。 A.做什么 B.怎么做 C.何时做 D.为谁做(2)WBS非常重要,下列哪项不是其很重要的原因(D)。 A.帮助组织工作 B.防止遗漏工作 C.为项目估算提供…...

Docker-Compose:教你入门到精通
引言 在当今的软件开发和运维领域,容器技术已经成为了一种非常重要的技术。而Docker-Compose作为Docker的重要工具之一,可以帮助我们轻松地管理和运行容器化的应用程序。本文将详细介绍Docker-Compose的入门到精通知识,帮助你更好地掌握这项技…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
