基于时域有限差分法的FDTD的计算电磁学算法(含Matlab代码)-YEE网格下的更新公式推导
基于时域有限差分法的FDTD的计算电磁学算法(含Matlab代码)-YEE网格下的更新公式推导
参考书籍:The finite-difference time-domain method for electromagnetics with MATLAB simulations(国内翻译版本:MATLAB模拟的电磁学时域有限差分法)
代码推荐:The finite-difference time-domain method for electromagnetics with MATLAB simulations的附件代码
我最初也是基于这个代码学习的
FDTD算法:采用差分直接离散时域Maxwell方程,电磁场的求解基于时间步的迭代,无需存储全空间的电磁场信息,内存消耗较小,同时采用立方体网格和差分算法,网格形式和算法均十分简单,计算速度快,基于时域算法,特别适合“宽带问题”的求解。但是,简单的立方体方体网格带来的弊端就是模型拟合精度较低,对于含有精细结构的模型,计算精度较低,同时基于“微分方程”,计算区域需要设置截断。
详细对比参考:常用计算电磁学算法特性与电磁软件分析
1、从麦克斯韦开始的FDTD时域有限差分法
1.1 麦克斯韦方程
FDTD叫时域有限差分法,显然,其依赖的麦克斯韦方程也是时域的。麦克斯韦时域微分方程为:
∇ × H = ∂ D ∂ t + J ∇ × E = − ∂ B ∂ t − M ∇ ⋅ D = ρ e ∇ ⋅ B = ρ m \begin{gathered} \nabla\times \mathbf{H}= {\frac{\partial \mathbf{D}}{\partial t}}+\boldsymbol{J} \\ \nabla\times \mathbf{E}=-{\frac{\partial \mathbf{B}}{\partial t}}-\mathbf{M} \\ \nabla\cdot\mathbf{D}=\rho_{\mathrm{e}} \\ \nabla\cdot \mathbf{B}=\rho_{m} \end{gathered} ∇×H=∂t∂D+J∇×E=−∂t∂B−M∇⋅D=ρe∇⋅B=ρm
式中,E为电场强度(V/m);D为电位移(C/m);H为磁场强度(A/m);B为磁通量密度(Wb/m°);J为电流密度(A/m);M为磁流密度(V/m); ρ e \rho_{e} ρe为电荷密度(C/m); ρ m \rho_{m} ρm为磁荷密度(Wb/m)。
依稀记得当时老师说,麦克斯韦方程有其直观理解,分别是:
1. 变化的电场和电流会产生磁场
2. 变化的磁场和磁荷会产生电场(自然界无磁荷,一般是等效出来)
3. 电流源产生电场
4. 磁流源产生磁场
1.2 本构关系
本构关系对补充麦克斯韦方程和描述媒质的特性是必要的,本构关系对线性、各向同性和非色散媒质可以写成:
D = ε E B = μ H . \begin{aligned}D&=\varepsilon E\\B&=\mu H\end{aligned}. DB=εE=μH.
其中, ε \varepsilon ε为媒质的介电常数; μ \mu μ为媒质的磁导率。在自由空间,有:
ε = ε 0 = 8.854 × 1 0 − 12 F / m μ = μ 0 = 4 π × 1 0 − 7 H / m \begin{aligned}\varepsilon=&\varepsilon_0=8.854\times10^{-12}\quad\mathrm{F/m}\\\mu=&\mu_0=4\pi\times10^{-7}\quad\mathrm{H/m}\end{aligned} ε=μ=ε0=8.854×10−12F/mμ0=4π×10−7H/m
在常规的电磁学表述中,我们更多的使用相对介电常数。比如说耳熟能详的FR4板材,其相对介电常数大概是 ε r = 4.2 \varepsilon_r=4.2 εr=4.2。 这就代表其实际的介电常数为 ε F R 4 = ε r ε 0 \varepsilon_{FR4}=\varepsilon_r\varepsilon_0 εFR4=εrε0。但是,还有一个重要参数和本构关系相关,那就是损耗角正切 t a n δ tan \delta tanδ。
对于FR4板材,一般认为其损耗角正切为 t a n δ = 0.02 tan \delta=0.02 tanδ=0.02,根据微波工程1.3小节的公式:
ϵ = ϵ ′ − j ϵ ′ ′ = ϵ ′ ( 1 − j tan δ ) = ϵ 0 ϵ r ( 1 − j tan δ ) \epsilon=\epsilon^{\prime}-j\epsilon^{\prime\prime}=\epsilon^{\prime}(1-j\tan\delta)=\epsilon_{0}\epsilon_{r}(1-j\tan\delta) ϵ=ϵ′−jϵ′′=ϵ′(1−jtanδ)=ϵ0ϵr(1−jtanδ),其对应的介电常数应该是:
ε F R 4 = ε r ( 1 − j tan δ ) ε 0 = ( 4.2 − j 0.02 ) ε 0 \varepsilon_{FR4}=\varepsilon_r(1-j\tan\delta)\varepsilon_0=(4.2-j0.02)\varepsilon_0 εFR4=εr(1−jtanδ)ε0=(4.2−j0.02)ε0
其对应的相对介电常数为:4.2-j0.02
在进行FDTD的推导时,因为在 FDTD 的更新方程的过程中满足散度方程,所以只需要考虑两个旋度方程即可。麦克斯韦中的电流密度 J \boldsymbol{J} J等于导体电流密度 J c \boldsymbol{J_c} Jc与施加电流密度 J i \boldsymbol{J_i} Ji之和,即:
J = J c + J i \boldsymbol{J}=\boldsymbol{J_{\mathrm{c}}}+\boldsymbol{J_{\mathrm{i}}} J=Jc+Ji
对于磁流密度,也类似:
M = M c + M i \boldsymbol{M}=\boldsymbol{M_{\mathrm{c}}}+\boldsymbol{M_{\mathrm{i}}} M=Mc+Mi
因此,对原来的麦克斯韦方程拆分一下,就是:
∇ × H = ε ∂ E ∂ t + σ e E + J i \nabla\times \boldsymbol{H}=\varepsilon\frac{\partial \boldsymbol{E}}{\partial t}+\sigma^{e}\boldsymbol{E}+\boldsymbol{J_{i}} ∇×H=ε∂t∂E+σeE+Ji
和:
∇ × E = − μ ∂ H ∂ t − σ m H − M i \nabla\times \boldsymbol{E}=-\mu\frac{\partial \boldsymbol{H}}{\partial t}-\sigma^{m}\boldsymbol{H}-\boldsymbol{M_{i}} ∇×E=−μ∂t∂H−σmH−Mi
旋度的计算公式大家还记得不:
∇ × F ( x , y , z ) = ∣ i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z F x F y F z ∣ = ( ∂ F z ∂ y − ∂ F y ∂ z ) i ^ + ( ∂ F x ∂ z − ∂ F z ∂ x ) j ^ + ( ∂ F y ∂ x − ∂ F x ∂ y ) k ^ \begin{aligned} &\nabla\times\mathbf{F}(x,y,z)=\begin{vmatrix}\hat{\boldsymbol{i}}&\hat{\boldsymbol{j}}&\hat{\boldsymbol{k}}\\\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\F_x&F_y&F_z\end{vmatrix} \\ &=\left(\frac{\partial F_z}{\partial y}-\frac{\partial F_y}{\partial z}\right)\hat{\boldsymbol{i}}+\left(\frac{\partial F_x}{\partial z}-\frac{\partial F_z}{\partial x}\right)\hat{\boldsymbol{j}}+\left(\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}\right)\hat{\boldsymbol{k}} \end{aligned} ∇×F(x,y,z)= i^∂x∂Fxj^∂y∂Fyk^∂z∂Fz =(∂y∂Fz−∂z∂Fy)i^+(∂z∂Fx−∂x∂Fz)j^+(∂x∂Fy−∂y∂Fx)k^
把麦克斯韦旋度方程按照三个方向x,y,z全部展开,就可以得到6个方程:
∂ E x ∂ t = 1 ε x ( ∂ H z ∂ y − ∂ H y ∂ z − σ x e E x − J i x ) ∂ E y ∂ t = 1 ε y ( ∂ H x ∂ z − ∂ H z ∂ x − σ y e E y − J i y ) ∂ E z ∂ t = 1 ε z ( ∂ H y ∂ x − ∂ H x ∂ y − σ z e E z − J i z ) ∂ H x ∂ t = 1 μ x ( ∂ E y ∂ z − ∂ E z ∂ y − σ x m H x − M i x ) ∂ H y ∂ t = 1 μ y ( ∂ E x ∂ x − ∂ E x ∂ z − σ y m H y − M i y ) ∂ H z ∂ t = 1 μ z ( ∂ E x ∂ y − ∂ E y ∂ x − σ z m H z − M i z ) \begin{gathered} \frac{\partial\boldsymbol{E}_x}{\partial t}= \frac1{\varepsilon_x}\Big(\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z}-\sigma_x^eE_x-J_{ix}\Big) \\ \frac{\partial E_y}{\partial t}= \frac1{\varepsilon_y}\Big(\frac{\partial H_x}{\partial z}-\frac{\partial H_z}{\partial x}-\sigma_y^eE_y-J_{iy}\Big) \\ \frac{\partial E_z}{\partial t}= \frac{1}{\varepsilon_{z}}\Big(\frac{\partial H_{y}}{\partial x}-\frac{\partial H_{x}}{\partial y}-\sigma_{z}^{e}E_{z}-J_{iz}\Big) \\ \frac{\partial H_x}{\partial t}= \frac1{\mu_x}\Big(\frac{\partial E_y}{\partial z}-\frac{\partial E_z}{\partial y}-\sigma_x^mH_x-M_{ix}\Big) \\ \frac{\partial H_y}{\partial t}= \frac1{\mu_y}\Big(\frac{\partial\boldsymbol{E}_x}{\partial x}-\frac{\partial\boldsymbol{E}_x}{\partial\boldsymbol{z}}-\boldsymbol{\sigma}_y^\mathfrak{m}H_y-\boldsymbol{M}_{iy}\Big) \\ \frac{\partial H_z}{\partial t}= \frac{1}{\mu_{z}}\Big(\frac{\partial\boldsymbol{E}_{x}}{\partial y}-\frac{\partial\boldsymbol{E}_{y}}{\partial x}-\sigma_{z}^{\mathfrak{m}}H_{z}-\boldsymbol{M}_{iz}\Big) \end{gathered} ∂t∂Ex=εx1(∂y∂Hz−∂z∂Hy−σxeEx−Jix)∂t∂Ey=εy1(∂z∂Hx−∂x∂Hz−σyeEy−Jiy)∂t∂Ez=εz1(∂x∂Hy−∂y∂Hx−σzeEz−Jiz)∂t∂Hx=μx1(∂z∂Ey−∂y∂Ez−σxmHx−Mix)∂t∂Hy=μy1(∂x∂Ex−∂z∂Ex−σymHy−Miy)∂t∂Hz=μz1(∂y∂Ex−∂x∂Ey−σzmHz−Miz)
2、空间差分与时间差分
2.1、非常简单的差分方程
FDTD是在离散网格中进行迭代的,上面的麦克斯韦公式有大量的求导计算,这该如何解决呢?答案是差分近似。大家学高数都学过导数的近似吧:
f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x f^{'}(x)=\underset{\Delta x\to0}{\operatorname*{lim}}\frac{f(x+\Delta x)-f(x)}{\Delta x} f′(x)=Δx→0limΔxf(x+Δx)−f(x)
如果 Δ x \Delta x Δx非常小,那么:
f ′ ( x ) ≈ f ( x + Δ x ) − f ( x ) Δ x f^{'}(x)\approx\frac{f(x+\Delta x)-f(x)}{\Delta x} f′(x)≈Δxf(x+Δx)−f(x)
但是为了实现更高的精度,所以采用FDTD都会采用双向差分公式:
f ′ ( x ) ≈ f ( x + Δ x ) − f ( x − Δ x ) 2 Δ x f^{^{\prime}}(x){\approx}\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x} f′(x)≈2Δxf(x+Δx)−f(x−Δx)
实际上,此处使用的是近似,也存在高阶的FDTD的算法,对于此近似考虑了更多项,精度会更高(参考“基于高阶时域有限差分法平面波及完全匹配层的研究”等):
f ′ ( x ) = f ( x + Δ x ) − f ( x − Δ x ) 2 Δ x − ( Δ x 2 ) 6 + . . . = f ( x + Δ x ) − f ( x − Δ x ) 2 Δ x + O ( ( Δ x ) 2 ) f^{\prime}(x)=\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}-\frac{(\Delta x^{2})}{6}+...=\frac{f(x+\Delta x)-f(x-\Delta x)}{2\Delta x}+O((\Delta x)^{2}) f′(x)=2Δxf(x+Δx)−f(x−Δx)−6(Δx2)+...=2Δxf(x+Δx)−f(x−Δx)+O((Δx)2)
2.2、差分方程的运用
在FDTD算法中,网格被剖分为YEE网格的形式,电场和磁场元胞差半个身位,其更新的时间步也是差 0.5 Δ t 0.5\Delta t 0.5Δt:
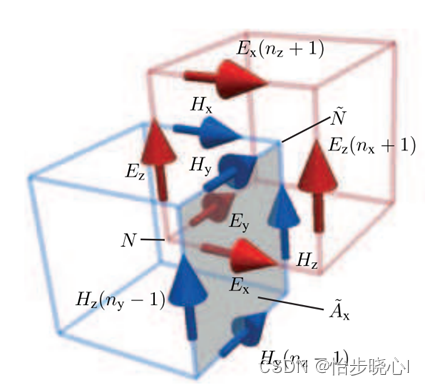
具体来讲,实际的电场网格和磁场网格的位置是:
E x ( i , j , k ) ⇒ ( ( i − 0 , 5 ) Δ x , ( j − 1 ) Δ y , ( k − 1 ) Δ z ) E y ( i , j , k ) ⇒ ( ( i − 1 ) Δ x , ( j − 0.5 ) Δ y , ( k − 1 ) Δ z ) E z ( i , j , k ) ⇒ ( ( i − 1 ) Δ x , ( j − 1 ) Δ y , ( k − 0.5 ) Δ z ) H x ( i , j , k ) ⇒ ( ( i − 1 ) Δ x , ( j − 0.5 ) Δ y , ( k − 0.5 ) Δ z ) H y ( i , j , k ) ⇒ ( ( i − 0.5 ) Δ x , ( j − 1 ) Δ y , ( k − 0.5 ) Δ z ) H z ( i , j , k ) ⇒ ( ( i − 0.5 ) Δ x , ( j − 0.5 ) Δ y , ( k − 1 ) Δ z ) \begin{aligned} E_x(i,j,k)\Rightarrow\left((i-0,5)\Delta x,(j-1)\Delta y,(k-1)\Delta z\right)\\ E_y(i,j,k)\Rightarrow\left((i-1)\Delta x,(j-0.5)\Delta y,(k-1)\Delta z\right)\\ E_z(i,j,k)\Rightarrow\left((i-1)\Delta x,(j-1)\Delta y,(k-0.5)\Delta z\right)\\ H_x(i,j,k)\Rightarrow\left((i-1)\Delta x,(j-0.5)\Delta y,(k-0.5)\Delta z\right)\\ H_y(i,j,k)\Rightarrow((i-0.5)\Delta x,(j-1)\Delta y,(k-0.5)\Delta z) \\ H_z(i,j,k)\Rightarrow((i-0.5)\Delta x,(j-0.5)\Delta y,(k-1)\Delta z) \end{aligned} Ex(i,j,k)⇒((i−0,5)Δx,(j−1)Δy,(k−1)Δz)Ey(i,j,k)⇒((i−1)Δx,(j−0.5)Δy,(k−1)Δz)Ez(i,j,k)⇒((i−1)Δx,(j−1)Δy,(k−0.5)Δz)Hx(i,j,k)⇒((i−1)Δx,(j−0.5)Δy,(k−0.5)Δz)Hy(i,j,k)⇒((i−0.5)Δx,(j−1)Δy,(k−0.5)Δz)Hz(i,j,k)⇒((i−0.5)Δx,(j−0.5)Δy,(k−1)Δz)
更新的时间步也是差 0.5 Δ t 0.5\Delta t 0.5Δt:FDTD算法在离散的时间瞬间取样和计算场值,但是电场和磁场取样计算并不是在相同的时刻。对时间步 Δ t \Delta t Δt,电场E的取样时刻为:0, Δ t \Delta t Δt,2 Δ t \Delta t Δt,3 Δ t \Delta t Δt,…,n Δ t \Delta t Δt;而磁场H取样时刻为:0.5 Δ t \Delta t Δt,1.5 Δ t \Delta t Δt,2.5 Δ t \Delta t Δt,…(n+0.5) Δ t \Delta t Δt。即电场取样在时间的整数步长时刻,而磁场取样时刻为半整数时间步时刻。它们之间的时间差为半个时间步。
因此,考虑一个上面得到的麦克斯韦的方程(以Ex方向为例):
∂ E x ∂ t = 1 ε x ( ∂ H z ∂ y − ∂ H y ∂ z − σ x e E x − J i r ) \frac{\partial E_x}{\partial t}=\frac1{\varepsilon_x}\left(\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z}-\sigma_x^eE_x-J_{ir}\right) ∂t∂Ex=εx1(∂y∂Hz−∂z∂Hy−σxeEx−Jir)
观察其导数项,分别有时间的差分项 ∂ E x ∂ t \frac{\partial E_x}{\partial t} ∂t∂Ex和空间的差分项 ∂ H z ∂ y \frac{\partial H_z}{\partial y} ∂y∂Hz和 ∂ H y ∂ z \frac{\partial H_y}{\partial z} ∂z∂Hy。
方程中的导数可以用中心差分来近似,此时 E x n ( i , j , k ) E_x^n(i,j,k) Exn(i,j,k)的位置为中心差分公式的中心点,而时间上应以 ( n + 0.5 ) Δ t (n+0.5)\Delta t (n+0.5)Δt作为中心点(因为电场E的取样时刻为:0, Δ t \Delta t Δt,2 Δ t \Delta t Δt,3 Δ t \Delta t Δt,…,n Δ t \Delta t Δt,而 ( n + 0.5 ) Δ t (n+0.5)\Delta t (n+0.5)Δt差分后可以得到n和n+1,符合取样时刻)。因此,第一项 ∂ E x ∂ t \frac{\partial E_x}{\partial t} ∂t∂Ex可以写成如下的差分形式:
E x n + 0.5 ( i , j , k ) = E x n + 1 ( i , j , k ) − E x n ( i , j , k ) Δ t E_x^{n+0.5}(i,j,k)=\frac{E_x^{n+1}(i,j,k)-E_x^n(i,j,k)}{\Delta t} Exn+0.5(i,j,k)=ΔtExn+1(i,j,k)−Exn(i,j,k)
而空间的差分项 ∂ H z ∂ y \frac{\partial H_z}{\partial y} ∂y∂Hz可以写成:
∂ H z ∂ y = H z n + 1 2 ( i , j , k ) − H z n + 1 2 ( i , j − 1 , k ) Δ y \frac{\partial H_z}{\partial y}=\frac{H_z^{n+\frac12}(i,j,k)-H_z^{n+\frac12}(i,j-1,k)}{\Delta y} ∂y∂Hz=ΔyHzn+21(i,j,k)−Hzn+21(i,j−1,k)
2.3、得到差分方程
把所有项都写成差分形式,就可以得到3D的FDTD更新方程:
E x n + 1 ( i , j , k ) = C e x e ( i , j , k ) × E x n ( i , j , k ) + C e x h z ( i , j , k ) × ( H z n + 1 2 ( i , j , k ) − H z n + 1 2 ( i , j − 1 , k ) ) + C e x h y ( i , j , k ) × ( H y n + 1 2 ( i , j , k ) − H y n + 1 2 ( i , j , k − 1 ) ) + C e x j ( i , j , k ) × J i x n + 1 2 ( i , j , k ) \begin{aligned} E_{x}^{n+1}\left(i,j,k\right)& =C_{exe}(i,j,k)\times E_x^n(i,j,k) \\ &+C_{exhz}(i,j,k)\times(H_{z}^{n+\frac12}(i,j,k)-H_{z}^{n+\frac12}(i,j-1,k)) \\ &+C_{\mathrm{exhy}}(i,j,k)\times(H_y^{n+\frac12}(i,j,k)-H_y^{n+\frac12}(i,j,k-1)) \\ &+C_{exj}\left(i,j,k\right)\times J_{ix}^{n+\frac12}(i,j,k) \end{aligned} Exn+1(i,j,k)=Cexe(i,j,k)×Exn(i,j,k)+Cexhz(i,j,k)×(Hzn+21(i,j,k)−Hzn+21(i,j−1,k))+Cexhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i,j,k−1))+Cexj(i,j,k)×Jixn+21(i,j,k)
C开头的都是系数,为了书写方便,其实际的值为:
C e x e ( i , j , k ) = 2 ε z ( i , j , k ) − Δ t σ z e ( i , j , k ) 2 ε z ( i , j , k ) + Δ t σ z e ( i , j , k ) C e x h y ( i , j , k ) = 2 Δ t ( 2 ε z ( i , j , k ) + Δ t σ z e ( i , j , k ) ) Δ x C e x h y ( i , j , k ) = − 2 Δ t ( 2 ε z ( i , j , k ) + Δ t σ z e ( i , j , k ) ) Δ y C e x j ( i , j , k ) = − 2 Δ t 2 ε z ( i , j , k ) + Δ t σ z e ( i , j , k ) \begin{gathered} C_{exe}(i,j,k)= \frac{2\varepsilon_z(i,j,k)-\Delta t\sigma_z^e(i,j,k)}{2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k)} \\ C_{exhy}(i,j,k)= \frac{2\Delta t}{(2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k))\Delta x} \\ C_{{exhy}}(i,j,k)= -\frac{2\Delta t}{(2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k))\Delta y} \\ C_{exj}\left(i,j,k\right) =-\frac{2\Delta t}{2\varepsilon_z(i,j,k)+\Delta t\sigma_z^e(i,j,k)} \end{gathered} Cexe(i,j,k)=2εz(i,j,k)+Δtσze(i,j,k)2εz(i,j,k)−Δtσze(i,j,k)Cexhy(i,j,k)=(2εz(i,j,k)+Δtσze(i,j,k))Δx2ΔtCexhy(i,j,k)=−(2εz(i,j,k)+Δtσze(i,j,k))Δy2ΔtCexj(i,j,k)=−2εz(i,j,k)+Δtσze(i,j,k)2Δt
当然,这只是6个方程中的一个,更加详细的方程参考:
MATLAB模拟的电磁学时域有限差分法的1.3。看看对应的matlab代码是怎么写的(没有电流就可以省略Cexj):
current_time = current_time + dt/2;Ex(1:nx,2:ny,2:nz) = Cexe(1:nx,2:ny,2:nz).*Ex(1:nx,2:ny,2:nz) ...+ Cexhz(1:nx,2:ny,2:nz).*...(Hz(1:nx,2:ny,2:nz)-Hz(1:nx,1:ny-1,2:nz)) ...+ Cexhy(1:nx,2:ny,2:nz).*...(Hy(1:nx,2:ny,2:nz)-Hy(1:nx,2:ny,1:nz-1));
% General electric field updating coefficients
% Coeffiecients updating Ex
Cexe = (2*eps_r_x*eps_0 - dt*sigma_e_x) ..../(2*eps_r_x*eps_0 + dt*sigma_e_x);
Cexhz = (2*dt/dy)./(2*eps_r_x*eps_0 + dt*sigma_e_x);
Cexhy = -(2*dt/dz)./(2*eps_r_x*eps_0 + dt*sigma_e_x);相关文章:

基于时域有限差分法的FDTD的计算电磁学算法(含Matlab代码)-YEE网格下的更新公式推导
基于时域有限差分法的FDTD的计算电磁学算法(含Matlab代码)-YEE网格下的更新公式推导 参考书籍:The finite-difference time-domain method for electromagnetics with MATLAB simulations(国内翻译版本:MATLAB模拟的电…...

win10使用debug,汇编初学
DOSBox挂载Debug.exe 双击 DOSBox Options.bat 打开配置 或者执行cmd DOSBox.exe -editconf notepad.exe -editconf %SystemRoot%\system32\notepad.exe -editconf %WINDIR%\notepad.exe最后一行增加 mount [盘符] [挂载的工作目录(debug.exe文件夹位置ÿ…...
怎么投稿各大媒体网站?
怎么投稿各大媒体网站?这是很多写作者及自媒体从业者经常面临的问题。在信息爆炸的时代,如何将自己的文章推送到广大读者面前,成为了一个不可避免的挑战。本文将为大家介绍一种简单有效的投稿方法——媒介库发稿平台发稿,帮助大家…...
chatgpt免费使用的网站
前言 如果您认为本文对你有帮助,希望可以点赞收藏!感谢您的支持 下面我为你推荐我自己在用的gpt类工具,帮你在工作学习生活上解决一些大小问题 🎉智能GPT 地址: https://meet.adminjs.net 在他的详情中有详细的使用…...
音频编辑软件:Studio One 6 中文
Studio One 6是一款功能强大的数字音乐制作软件,为用户提供一站式音乐制作解决方案。它具有直观的界面和强大的音频录制、编辑、混音和制作功能,支持虚拟乐器、效果器和第三方插件,可帮助用户实现高质量的音乐创作和制作。同时,St…...

MySQL语句|使用UNION和UNION ALL合并两个或多个 SELECT 语句的结果集
文章目录 举个通用的例子举个实际的例子 在MySQL中, UNION 和 UNION ALL 是用于合并两个或多个 SELECT 语句的结果集的操作符。 UNION 会去除结果集中的重复行,返回唯一的行,而 UNION ALL 会返回所有的行,包括重复行。 举个通…...
UNRAID 优盘制作
使用方法和开心方法: 如果重启之后显示器有信号但是黑屏无法正常引导系统,此为九代以后主板快速开机(快速引导)UNRAID并不支持快速引导所以会直接卡黑屏。所以发现这种情况的时候请进BIOS关闭和开机快速引导或和快有关系的任何开…...
二、Java中SpringBoot组件集成接入【MySQL和MybatisPlus】
二、Java中SpringBoot组件集成接入【MySQL和MybatisPlus】 1.MySQL和MybatisPlus简介2.maven依赖3.配置1.在application.yaml配置中加入mysql配置2.新增Mybatis-Plus配置类 4.参考文章 1.MySQL和MybatisPlus简介 MySQL是一种开源的关系型数据库管理系统,被广泛应用…...

银行测试--------转账
转账 付款账号测试 付款账号是借记卡,也可以是活期存折信用卡,定期存折不能转出。一般在账号选择的时候进行屏蔽转出账户在销户,冻结,挂失等异常状态,不能进行转账付款账号金额不够 转账金额测试 0.01~…...

阿里云最新优惠券领取方法及优惠活动汇总
随着互联网的飞速发展,云服务已经成为企业和个人使用的重要基础设施。阿里云作为全球领先的云服务提供商,一直致力于为用户提供优质的云服务。为了回馈用户,阿里云会定期推出各种优惠券和优惠活动,本文将为大家介绍阿里云最新优惠…...

动态分配内存的风险
1. 悬挂指针问题 在指针释放之后要将指针置空 delete ptr; ptr nullptr;2.内存碎片问题 频繁的申请与释放小块内存会造成大量的内存碎片。 3.内存申请与释放问题 C与C的内存申请与释放最好不要混用。 4.复制内存 基本语法 void* memcpy(void* _Dst, void* _Src, size_…...

多行SQL转成单行SQL
如下图所示 将以上多行SQL转成单行SQL 正则表达式如下 (?s)$[^a-zA-Z()0-9]*结果如下 灵活使用,也未必只能使用Sublime Text...
wpf的资源路径
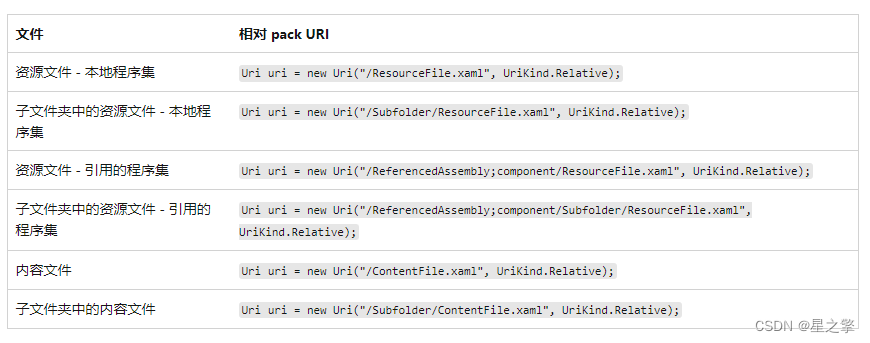
1、手动命名空间 xmlns:share"clr-namespace:***;assembly**" 2、资源文件 Pack URI 编译到本地程序集内的资源文件的 pack URI 使用以下授权和路径: 授权:application:///。 路径:资源文件的名称,包括其相对于本地…...
shell 脚本之一键部署安装 Nginx
定义一个变量来存放 nginx 版本号 version1.15.4nginx 下载地址:http://nginx.org/download/ 下列函数功能则是判断当前步骤是否执行成功,并将结果输出出来 function show_result(){if [ "$1" -eq 0 ]thenecho -e "\e[32m$2 is Succes…...
第01章_Java语言概述拓展练习(为什么要设置path?)
文章目录 第01章_Java语言概述拓展练习1、System.out.println()和System.out.print()有什么区别?2、一个".java"源文件中是否可以包括多个类?有什么限制?3、Something类的文件名叫OtherThing.java是否可以?4、为什么要设…...

手机直连卫星及NTN简介
一、手机直连卫星的发展现状 近日,华为推出了支持北斗卫星短报文的Mate 50旗舰机、P60系列,苹果也跟Globalstar(全球星)合作推出了支持卫星求救的iPhone14,最亮眼的还是华为的。这几款产品揭开了卫星通信探索消费领域…...
对git中tag, branch的重新理解
1. 问题背景 项目中之前一个tag(v1.0)打错了,想删除它,但我们从此tag v1.0中迁出新建分支Branch_v1.0,在此分支下修复了bug,想重新打一个tag v1.0,原来的tag v1.0可以删除掉吗? 错误的理解&am…...

python中none的替换方法:pandasnumpy
none的替换方法: 1.pandas # 将缺失的id值替换为None merged_df[id].fillna(None, inplaceTrue) #这行代码使用了Pandas库中的fillna方法,对DataFrame中的id列进行了填充操作。具体来说,它将该列中的缺失值用字符串None进行填充,…...
您与此网站之间建立的连接不安全
连接不安全的主要原因之一是使用不安全的通信协议。在互联网传输中,如果使用的协议不加密,那么数据就容易受到窃听和篡改。另一个可能的原因是网站没有正确配置其安全证书,使得用户的连接没有得到适当的加密保护。 解决方法: 采用…...
定义了导出函数,但dll中没有此函数)
__declspec (dllexport)定义了导出函数,但dll中没有此函数
这个一个比较低级的问题,为避免两次犯这样的低级错误,特此记录。 发生这个问题的原因是未包含头文件,例如: test.h //在头文件中声明了导出函数test() #ifdef __cplusplus extern "C" { #endif /*__cplusplus 1*/ext…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
