P1643 完美数 题解
完美数
首先,介绍一下这篇题解的特邀嘉宾:ChatGPT4.0
传送门
题目描述
考古队员小星在一次考察中意外跌入深渊,穿越到了一个神秘的荒漠。这里有许多超越他认识的事物存在,例如许多漂浮在空中的建筑,例如各种奇怪的动物。
在这片荒漠的中央,小星发现了一个巨大的类似神庙的建筑,为了脱离这片空间,小星决定前去探索。
在临近神庙大门时,突然跳出了一个人面狮(不是斯芬达克斯)!它咆哮着:
“我是这里的守卫,要想通过这里,必须回答出我的一系列问题,否则,我就吃了你。”
人面狮告诉小星,问题总是这样的模式:比 X X X 大的第 N N N 小的回文数是多少。
小星想,这个问题看来不难,于是问答开始了。
“比 1 1 1 大的第 1 1 1 小回文数数是多少?”
“ 2 2 2”
“比 17 17 17 大的第 2 2 2 小的回文数是多少?”
“ 33 33 33”
“比 98 98 98 大的第 2 2 2 小的回文数是多少?”
“ 101 101 101”
“那比 948237 大的第 2339587 小的回文数是多少?”
“*(•%(*•—#•#¥*—%(*—%”
为了避免被守卫吃掉,小星只好打开笔记本想借助电脑,却意外地发现可以通过网络(网通?电信?宇宙通?)找到你,于是这个问题就拜托给你了!
输入格式
本题每一个数据包含有多组数据。
对于每一个数据包,第一行一个数 T T T,表示总共有 T T T 组数据。
对于每一组数据,包括两行,第一行为 X X X,第二行为 N N N,表示当前询问是比 X 大的第 N 小的回文数是多少。
输出格式
对于每一组数据输出一行,表示询问的结果。
样例 #1
样例输入 #1
3
1
1
17
2
98
2
样例输出 #1
2
33
101
提示
【数据规模】
20 % 20 \% 20% 的数据满足 X ≤ 200000 X \le 200000 X≤200000, N ≤ 1000 N \le 1000 N≤1000。
30 % 30 \% 30% 的数据满足 X , N X, N X,N 在 longint 范围之内,且答案也在 longint 范围之内。
100 % 100 \% 100% 的数据满足 X , N ≤ 10 10000 X, N \le {10}^{10000} X,N≤1010000,答案 ≤ 10 20001 \le {10}^{20001} ≤1020001。 T ≤ 10 T \le 10 T≤10。
以上来自洛谷 以上来自洛谷 以上来自洛谷
解题思路(所有思路与代码都由ChatGPT特供,本人只加以润色)
暴力思路(ChatGPT友情赞助)
- 首先需要找到比X大的第N小的回文数,可以从X+1开始逐个判断是否是回文数,直到找到第N个回文数为止。
- 判断一个数是否是回文数可以将其转化为字符串,然后判断字符串是否是回文字符串。
- 找到第N个回文数后输出即可。
伪代码:
- 读入T
- 循环T次:
- 读入X和N
- 初始化count为0,ans为0
- 从X+1开始逐个判断是否是回文数,直到count等于N为止:
- 将当前数转化为字符串
- 判断该字符串是否是回文字符串:
- 初始化i为0,j为字符串长度-1
- 循环i小于j:
- 如果字符串第i个字符不等于第j个字符,则不是回文字符串跳出循环
- 否则,i加1,j减1
- 如果i大于等于j,表示是回文字符串,将count加1
- 如果count等于N,表示找到了第N个回文数,将ans赋值为当前数
- 输出ans
Code1
#include <iostream>
#include <string>
using namespace std;bool isPalindrome(string num) {int i = 0, j = num.length() - 1;while (i < j) {if (num[i] != num[j]) {return false;}i++;j--;}return true;
}int main() {int T;cin >> T;for (int t = 0; t < T; t++) {int X, N;cin >> X >> N;int count = 0;int ans = 0;for (int num = X + 1; count < N; num++) {string numStr = to_string(num);if (isPalindrome(numStr)) {count++;ans = num;}}cout << ans << endl;}return 0;
}
暴力优化(依旧是ChatGPT大佬提供)
要降低时间复杂度,可以采用以下方法:
- 判断一个数是否是回文数,可以不用将其转化为字符串,而是直接在数字上进行操作。
- 可以利用回文数的对称性质来判断是否是回文数,即从两端往中间进行比较。
- 找到第N个回文数后,不需要继续判断后面的数,可以直接跳出循环。
Code2
#include <iostream>
using namespace std;bool isPalindrome(int num) {int reversedNum = 0;int temp = num;while (temp > 0) {int digit = temp % 10;reversedNum = reversedNum * 10 + digit;temp /= 10;}return num == reversedNum;
}int main() {int T;cin >> T;for (int t = 0; t < T; t++) {int X, N;cin >> X >> N;int count = 0;int ans = 0;for (int num = X + 1; count < N; num++) {if (isPalindrome(num)) {count++;ans = num;}}cout << ans << endl;}return 0;
}
继续优化(依然是它)
要进一步降低时间复杂度,可以采用以下方法:
- 判断一个数是否是回文数的操作可以进一步优化。可以只判断一半的数字,而不需要全部反转,然后与另一半进行比较。
- 可以通过找到下一个回文数的规律来快速找到第N个回文数。
优化后的代码如下:
Code3
#include <iostream>
using namespace std;bool isPalindrome(int num) {if (num < 0 || (num % 10 == 0 && num != 0)) {return false;}int reversedNum = 0;while (num > reversedNum) {reversedNum = reversedNum * 10 + num % 10;num /= 10;}return num == reversedNum || num == reversedNum / 10;
}int getNextPalindrome(int num) {num++;while (!isPalindrome(num)) {num++;}return num;
}int main() {int T;cin >> T;for (int t = 0; t < T; t++) {int X, N;cin >> X >> N;int ans = getNextPalindrome(X);for (int i = 1; i < N; i++) {ans = getNextPalindrome(ans);}cout << ans << endl;}return 0;
}
这样,我们通过优化判断回文数的方式以及找到下一个回文数的规律,可以更快地找到第N个回文数,进一步降低时间复杂度。
加上高精度算法优化(是它)
要使用高精度算法优化,可以采用以下方法:
- 定义一个高精度整数类,可以实现大整数的加法、减法和乘法等操作。
- 在每次计算回文数时,将当前数字转化为高精度整数,进行高精度的加法操作,直到找到第N个回文数。
Code4(TLE 20)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;vector<int> add(vector<int>& a, vector<int>& b) {vector<int> res;int carry = 0;int n = max(a.size(), b.size());for (int i = 0; i < n; i++) {int sum = carry;if (i < a.size()) {sum += a[i];}if (i < b.size()) {sum += b[i];}res.push_back(sum % 10);carry = sum / 10;}if (carry) {res.push_back(carry);}return res;
}bool isPalindrome(vector<int>& num) {int n = num.size();for (int i = 0; i < n / 2; i++) {if (num[i] != num[n - 1 - i]) {return false;}}return true;
}vector<int> getNextPalindrome(vector<int>& num) {int carry = 1;int n = num.size();for (int i = 0; i < n; i++) {num[i] += carry;carry = num[i] / 10;num[i] %= 10;}if (carry) {num.push_back(carry);}return num;
}int main() {int T;cin >> T;for (int t = 0; t < T; t++) {vector<int> X;string str;cin >> str;for (int i = str.size() - 1; i >= 0; i--) {X.push_back(str[i] - '0');}int N;cin >> N;vector<int> ans = X;for (int i = 0; i < N; i++) {ans = getNextPalindrome(ans);while (!isPalindrome(ans)) {ans = getNextPalindrome(ans);}}for (int i = ans.size() - 1; i >= 0; i--) {cout << ans[i];}cout << endl;}return 0;
}
- 注:该程序经本人改造。
优化++(还是它)
要进一步优化该程序,我们可以通过以下方式来提高效率:
- 不需要每次都判断当前数是否是回文数,只需要在最后输出时判断即可。
- 在计算下一个回文数时,可以直接从当前数一半开始倒序复制,这样可以减少循环次数。
Code5(RE 30)(加上高精度就AC了)
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;vector<int> tmp(1, 0);void initialize() {for (int i = 0; i < 20000; i++) {tmp.push_back(-1);}
}int sum(int x) {if (tmp[x] != -1) {return tmp[x];}if (x % 2 == 0) {tmp[x] = (pow(10, x / 2) - 1) / 9 * 2;}if (x % 2 == 1) {tmp[x] = sum(x + 1) - pow(10, x / 2);}return tmp[x];
}pair<int, int> count(int x) {x = (x + 8) / 9;int i = to_string(x).length() - 9;if (i < 1) {i = 1;}while (true) {if (sum(i) >= x) {return make_pair(i, 9 * sum(i - 1));}i++;}
}int solve(int x) {pair<int, int> result = count(x);int cnt = result.first;int sum = result.second;int half = pow(10, (cnt + 1) / 2 - 1) + (x - sum - 1);if (cnt % 2 == 1) {string halfStr = to_string(half);return stoi(halfStr.substr(0, halfStr.length() - 1) + string(halfStr.rbegin(), halfStr.rend()));} else {string halfStr = to_string(half);return stoi(halfStr + string(halfStr.rbegin(), halfStr.rend()));}
}int rev(int x) {int sz = to_string(x).length();int Sum = sum(sz - 1) * 9;Sum += stoi(to_string(x).substr(0, (sz + 1) / 2)) - pow(10, sz / 2 + sz % 2 - 1);while (solve(Sum) <= x) {Sum++;}return Sum - 1;
}int main() {initialize();int T;cin >> T;for (int i = 0; i < T; i++) {int N, X;cin >> N >> X;cout << solve(X + rev(N)) << endl;}return 0;
}
AC Code
//Code5加上高精度
我之所以不给代码是为了你们养成勤于动手的好习惯
相关文章:

P1643 完美数 题解
完美数 首先,介绍一下这篇题解的特邀嘉宾:ChatGPT4.0 传送门 题目描述 考古队员小星在一次考察中意外跌入深渊,穿越到了一个神秘的荒漠。这里有许多超越他认识的事物存在,例如许多漂浮在空中的建筑,例如各种奇怪的…...
docker一键安装
1.把docker_compose_install文件夹放在任意路径; 2.chmod -R 777 install.sh 3.执行./install.sh 兼容:CentOS7.6、麒麟V10服务器版、统信UOS等操作系统。 下载地址(本人上传,免积分下载):https://downlo…...

模板管理支持批量操作,DataEase开源数据可视化分析平台v2.2.0发布
2024年1月8日,DataEase开源数据可视化分析平台正式发布v2.2.0版本。 这一版本的功能升级包括:在“模板管理”页面中,用户可以通过模板管理的批量操作功能,对已有模板进行快速重新分类、删除等维护操作;数据大屏中&…...
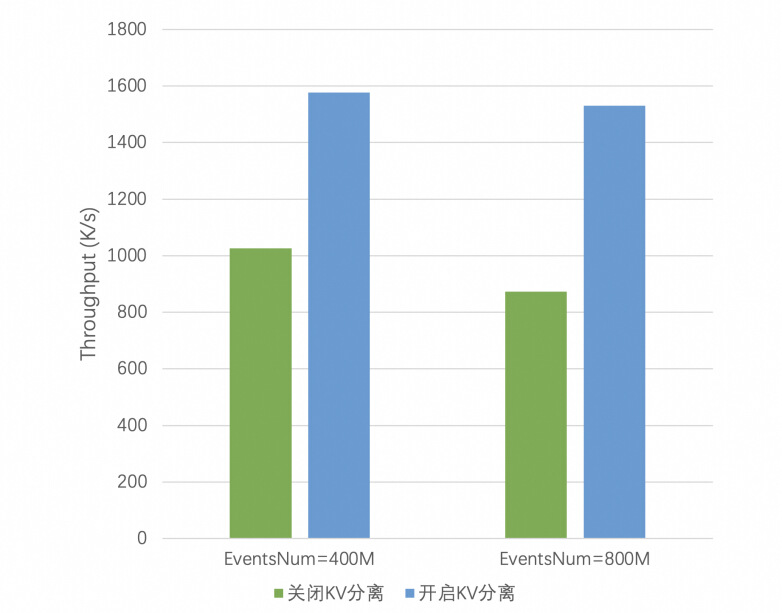
阿里云实时计算企业级状态存储引擎 Gemini 技术解读
本文整理自阿里云 Flink 存储引擎团队李晋忠,兰兆千,梅源关于阿里云实时计算企业级状态存储引擎 Gemini 的研究,内容主要分为以下五部分: 流计算状态访问的痛点企业级状态存储引擎GeminiGemini 性能评测&线上表现结语参考 一、…...
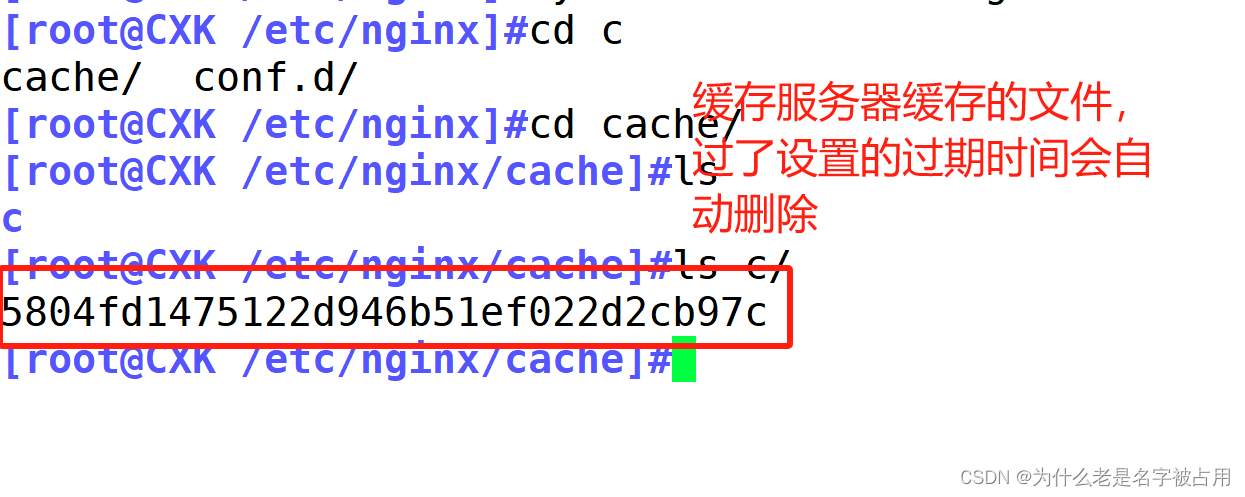
web缓存之nginx缓存
一、nginx缓存知识 网络缓存位于客户端和 "源服务器 "之间,保存着所有可见内容的副本。当客户端请求缓存中存储的内容时,它可以直接从缓存中检索内容,而无需与服务器通信。这样,网络缓存就 "接近 "了客户端&a…...
【用法总结】无障碍AccessibilityService
一、背景 本文仅用于做学习总结,转换成自己的理解,方便需要时快速查阅,深入研究可以去官网了解更多:官网链接点这里 之前对接AI语音功能时,发现有些按钮(或文本)在我没有主动注册唤醒词场景…...

AI绘画风格化实战
在社交软件和短视频平台上,我们时常能看到各种特色鲜明的视觉效果,比如卡通化的图片和中国风的视频剪辑。这些有趣的风格化效果其实都是图像风格化技术的应用成果。 风格化效果举例 MidLibrary 这个网站提供了不同的图像风格,每一种都带有鲜…...

008定点小数、奇偶校验码
...
一、二进制方式 安装部署K8S
目录 一、操作系统初始化 1、关闭防火墙 2、关闭 SELinu 3、 关闭 swap 4、添加hosts 5、同步系统时间 二、集群搭建 —— 使用外部Etcd集群 1、自签证书 2、自签 Etcd SSL 证书 ① 创建 CA 配置文件:ca-config.json ② 创建 CA 证书签名请求文件ÿ…...
【simple-admin】FMS模块如何快速接入阿里云oss 腾讯云cos 服务 实现快速上传文件功能落地
让我们一起支持群主维护simple-admin 社群吧!!! 不能加入星球的朋友记得来点个Star!! https://github.com/suyuan32/simple-admin-core 一、前提准备 1、goctls版本 goctls官方git:https://github.com/suyuan32/goctls 确保 goctls是最新版本 v1.6.19 goctls -v goct…...
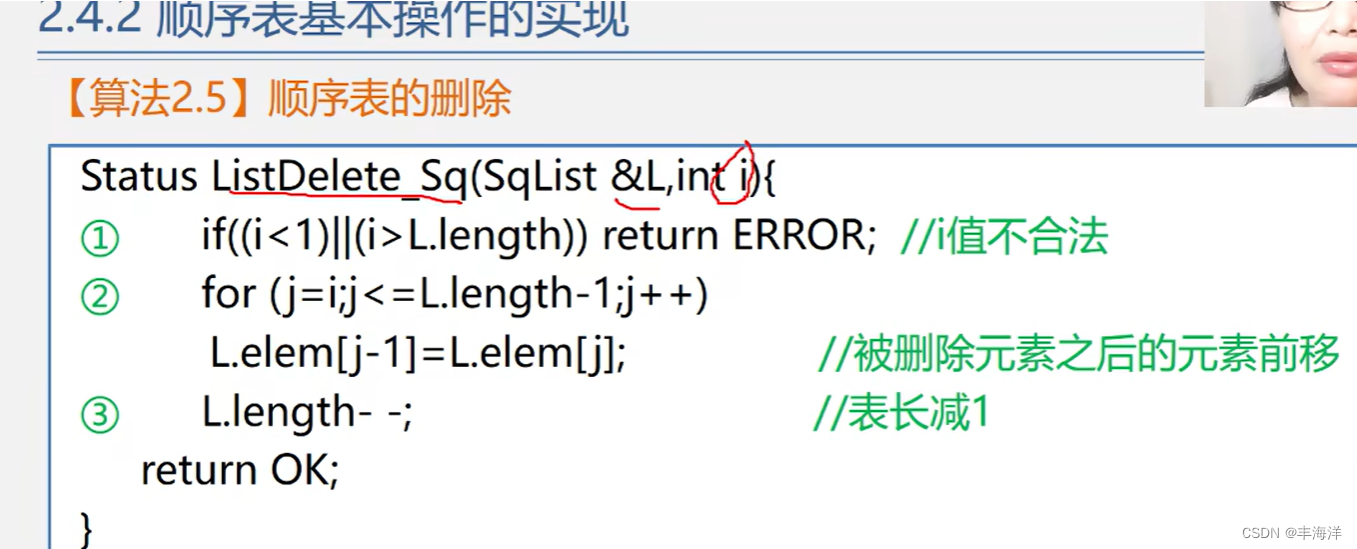
数据结构.线性表(2)
一、模板 例子: a: b: 二、基本操作的实现 (1)初始化 (2)销毁和清空 (3)求长度和判断是否为空 (4)取值 (5)查找 (6)插入 &…...

【计算机网络】TCP原理 | 可靠性机制分析(三)
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【网络编程】【Java系列】 本专栏旨在分享学习网络编程、计算机网络的一点学习心得,欢迎大家在评论区交流讨论💌 目…...

【昕宝爸爸小模块】线程的几种状态,状态之间怎样流转
➡️博客首页 https://blog.csdn.net/Java_Yangxiaoyuan 欢迎优秀的你👍点赞、🗂️收藏、加❤️关注哦。 本文章CSDN首发,欢迎转载,要注明出处哦! 先感谢优秀的你能认真的看完本文&…...
ChatGPT网站小蜜蜂AI更新了
ChatGPT网站小蜜蜂AI更新了 前阶段郭震兄弟刚开发小蜜蜂AI网站的的时候,写了一篇关于ChatGPT的网站小蜜蜂AI的博文[https://blog.csdn.net/weixin_41905135/article/details/135297581?spm1001.2014.3001.5501]。今天听说小蜜蜂网站又增加了新的功能——在线生成思…...

瑞_Java开发手册_(二)异常日志
文章目录 异常日志的意义(一) 错误码(二) 异常处理(三) 日志规约附:错误码列表 🙊前言:本文章为瑞_系列专栏之《Java开发手册》的异常日志篇,本篇章主要介绍异常日志的错误码、异常处理、日志规约。由于博主是从阿里的《Java开发手…...
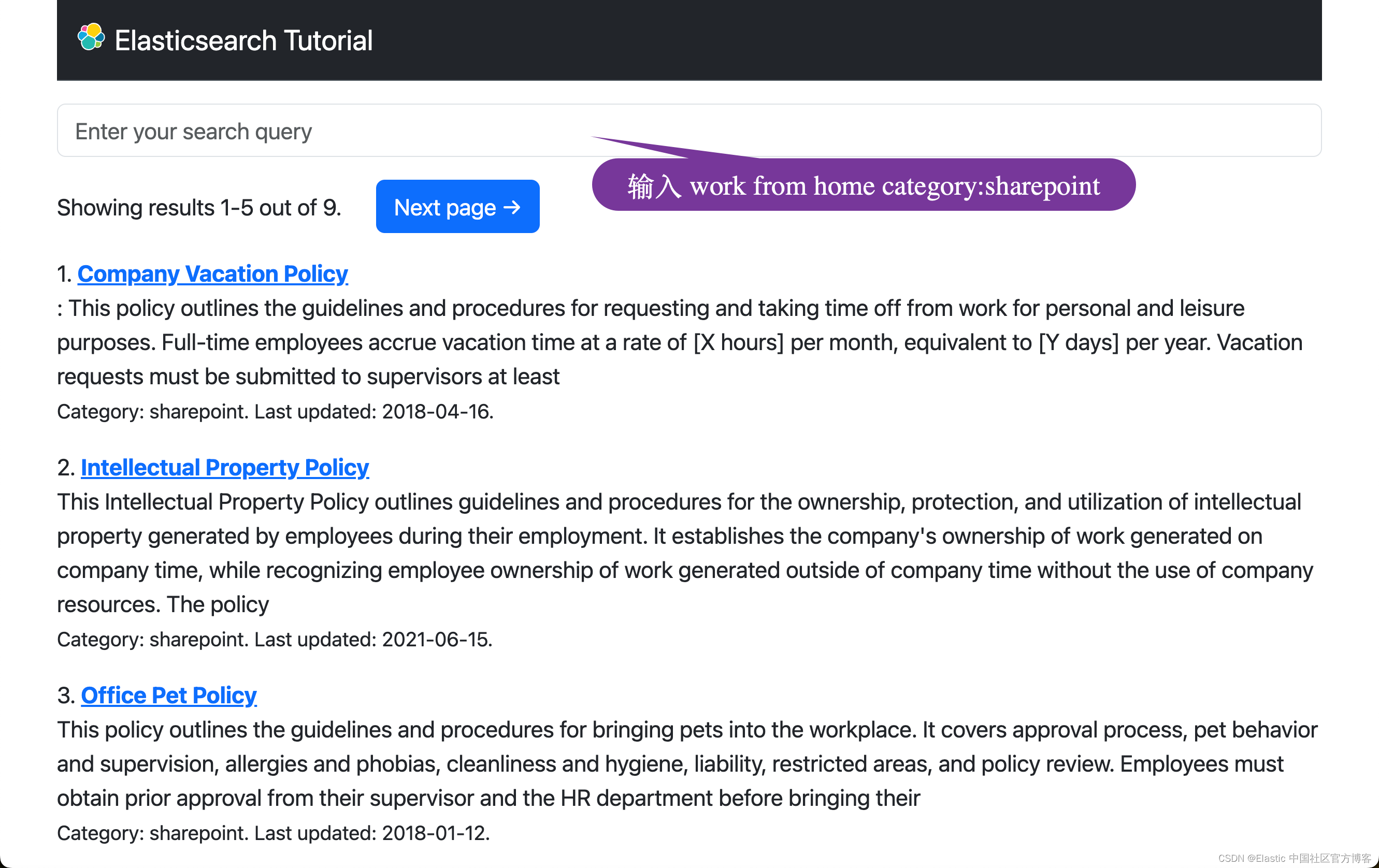
Elasticsearch:Search tutorial - 使用 Python 进行搜索 (四)
在本节中,你将了解另一种机器学习搜索方法,该方法利用 Elastic Learned Sparse EncodeR 模型或 ELSER,这是一种由 Elastic 训练来执行语义搜索的自然语言处理模型。这是继之前的文章 “Elasticsearch:Search tutorial - 使用 Pyth…...

Python之Matplotlib绘图调节清晰度
Python之Matplotlib绘图调节清晰度 文章目录 Python之Matplotlib绘图调节清晰度引言解决方案dpi是什么?效果展示总结 引言 使用python中的matplotlib.pyplot绘图的时候,如果将图片显示出来,或者另存为图片,常常会出现清晰度不够的…...

pygame.error: video system not initialized
错误处理方式: pygame.init() 增加此行...

java面试题2024
前言 准备换工作了,给自己定个目标,每天至少整理出一道面试题。题型会比较随机,感觉这样更容易随机到面试官要问的东西。整理时我会把我认为正确的回答写出来,比较复杂的也尽量把原理贴出来,争取做到无论为了应付面试&…...
配置git服务器
第一步: jdk环境配置 (1)搜索【高级系统设置】,选择【高级】选项卡,点【环境变量】 (2)在【系统变量】里面,点击【新建】 (3)添加JAVA_HOME环境变量JAVA_HO…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
