C++力扣题目538--把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: . - 力扣(LeetCode) 相同
示例 1:

输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1] 输出:[1,null,1]
示例 3:
输入:root = [1,0,2] 输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
思路
一看到累加树,相信很多小伙伴都会疑惑:如何累加?遇到一个节点,然后再遍历其他节点累加?怎么一想这么麻烦呢。
然后再发现这是一棵二叉搜索树,二叉搜索树啊,这是有序的啊。
那么有序的元素如何求累加呢?
其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。
为什么变成数组就是感觉简单了呢?
因为数组大家都知道怎么遍历啊,从后向前,挨个累加就完事了,这换成了二叉搜索树,看起来就别扭了一些是不是。
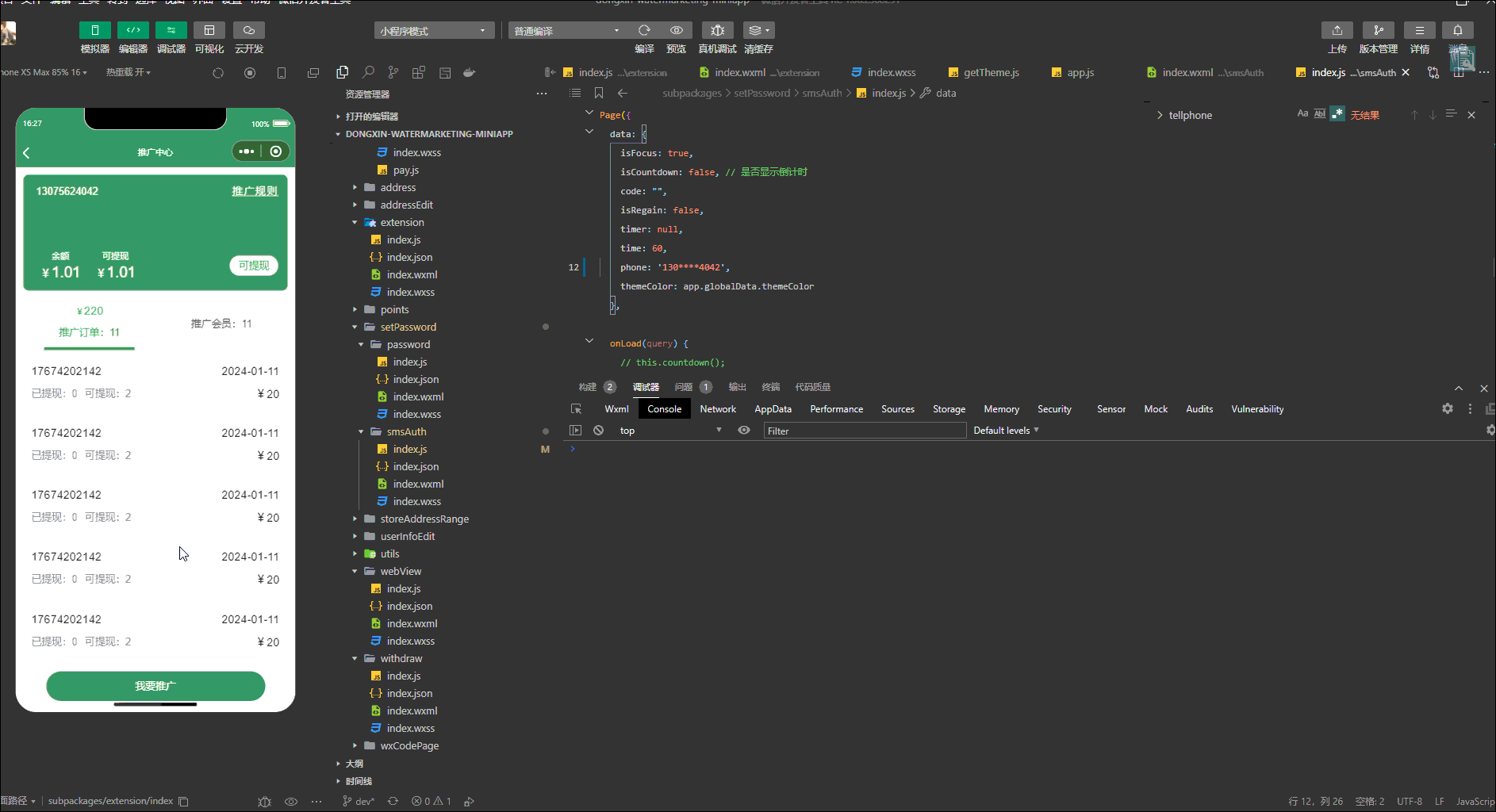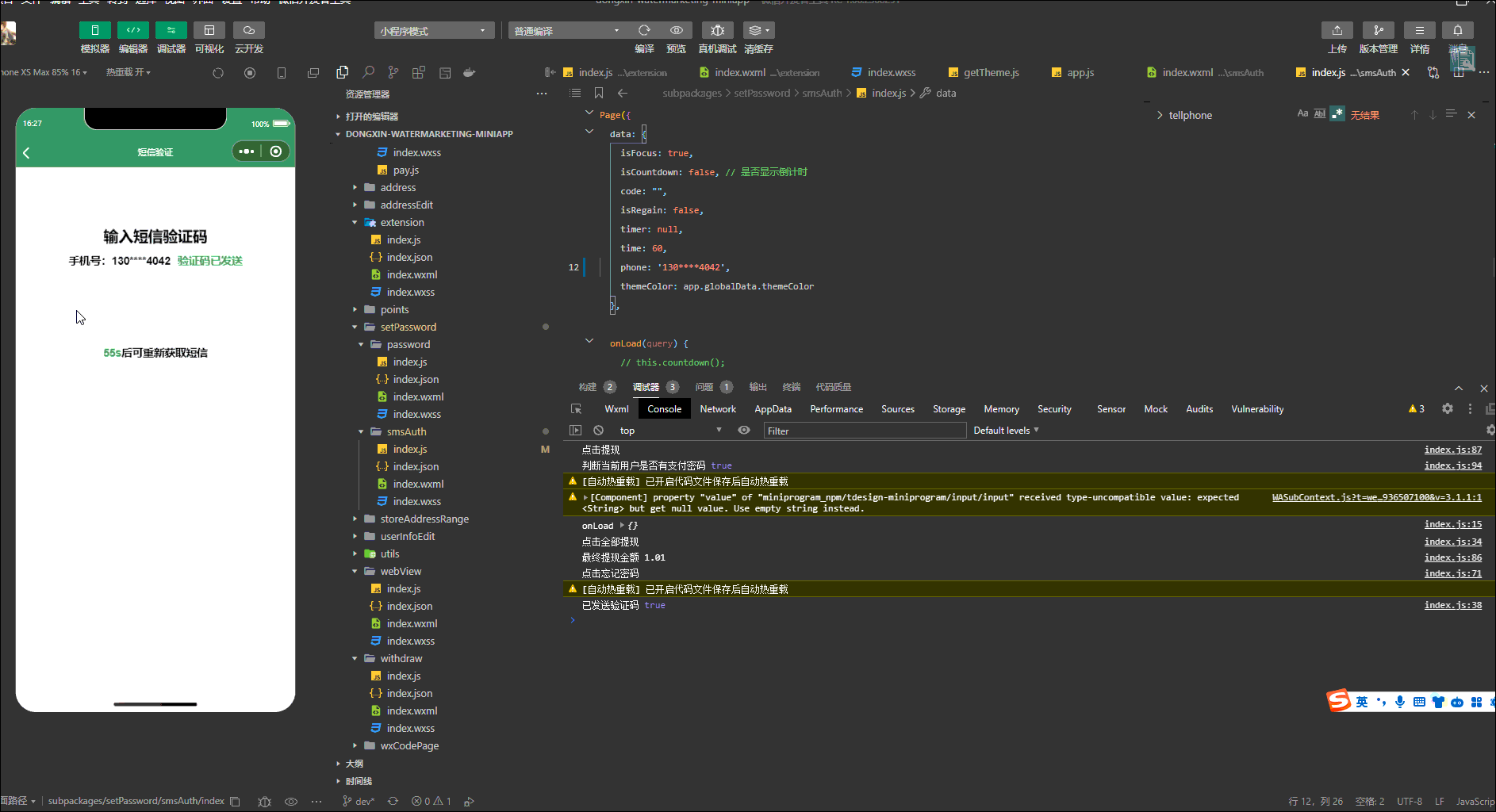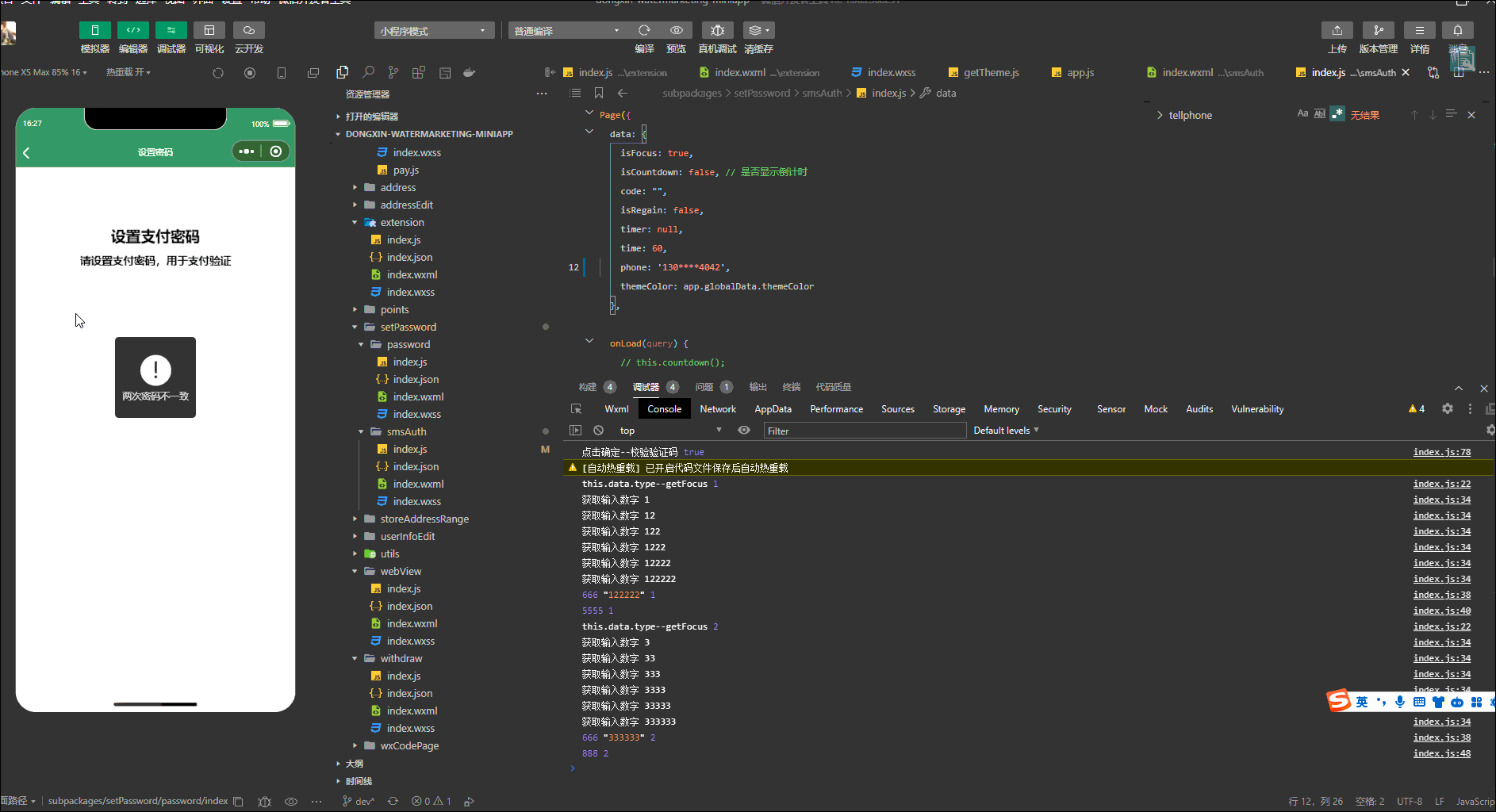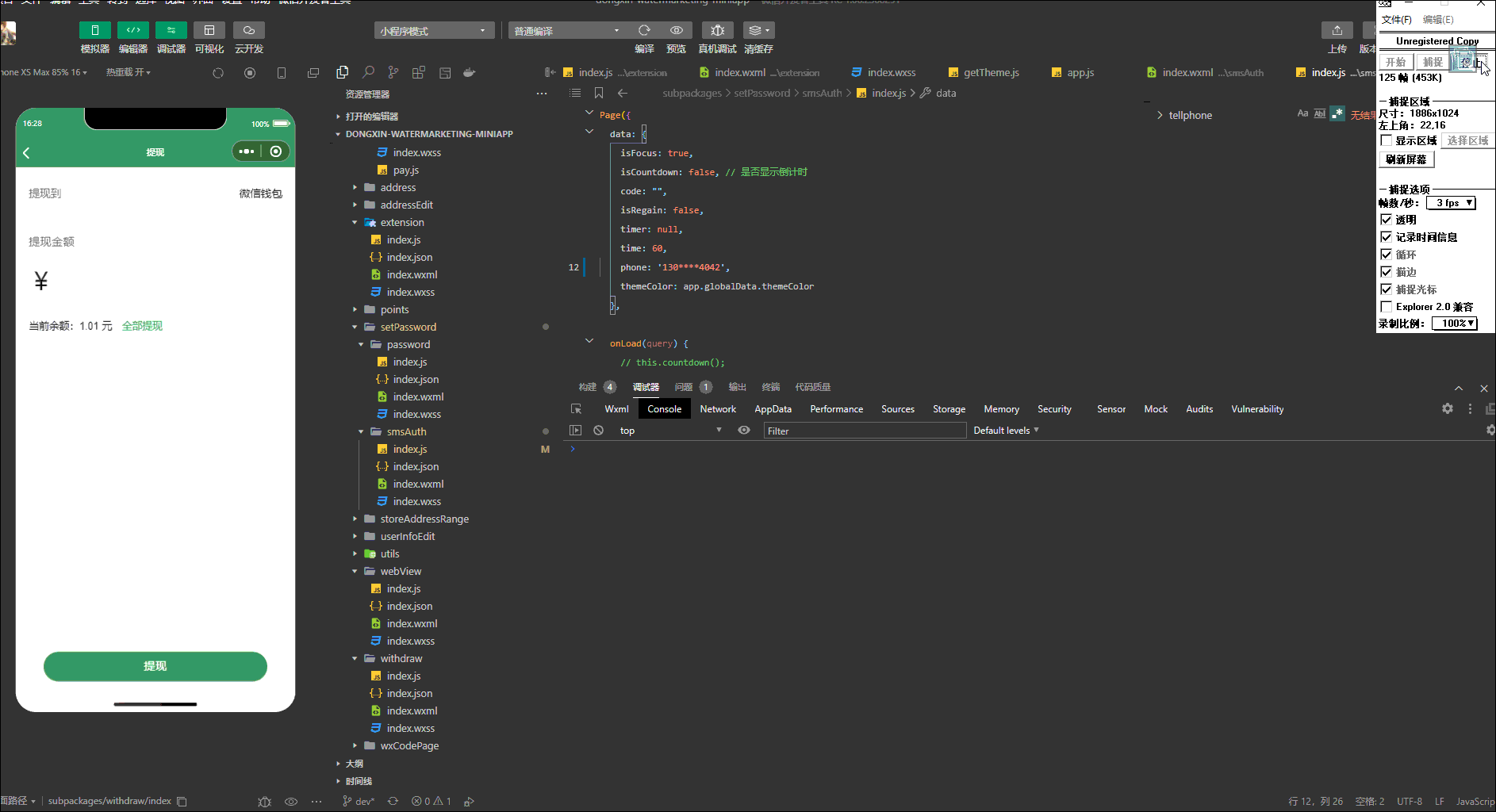
那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加就可以了。
#递归
遍历顺序如图所示:
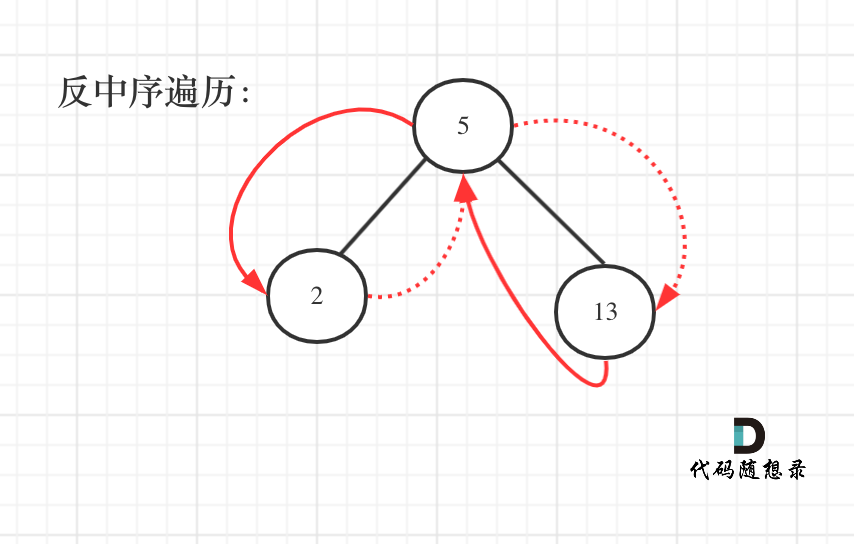
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
pre指针的使用技巧,我们在二叉树:搜索树的最小绝对差 (opens new window)和二叉树:我的众数是多少? (opens new window)都提到了,这是常用的操作手段。
- 递归函数参数以及返回值
这里很明确了,不需要递归函数的返回值做什么操作了,要遍历整棵树。
同时需要定义一个全局变量pre,用来保存cur节点的前一个节点的数值,定义为int型就可以了。
代码如下:
int pre = 0; // 记录前一个节点的数值
void traversal(TreeNode* cur)
- 确定终止条件
遇空就终止。
if (cur == NULL) return;
- 确定单层递归的逻辑
注意要右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
代码如下:
traversal(cur->right); // 右
cur->val += pre; // 中
pre = cur->val;
traversal(cur->left); // 左
递归法整体代码如下:
class Solution {
private:int pre = 0; // 记录前一个节点的数值void traversal(TreeNode* cur) { // 右中左遍历if (cur == NULL) return;traversal(cur->right);cur->val += pre;pre = cur->val;traversal(cur->left);}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};
#迭代法
迭代法其实就是中序模板题了,在二叉树:前中后序迭代法 (opens new window)和二叉树:前中后序统一方式迭代法 (opens new window)可以选一种自己习惯的写法。
这里我给出其中的一种,代码如下:
class Solution {
private:int pre; // 记录前一个节点的数值void traversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) {st.push(cur);cur = cur->right; // 右} else {cur = st.top(); // 中st.pop();cur->val += pre;pre = cur->val;cur = cur->left; // 左}}}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};
#总结
经历了前面各种二叉树增删改查的洗礼之后,这道题目应该比较简单了。
好了,二叉树已经接近尾声了,接下来就是要对二叉树来一个大总结了
相关文章:

C++力扣题目538--把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下,二叉搜索树满足下列约束条件&#…...

曲线生成 | 图解贝塞尔曲线生成原理(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 贝塞尔曲线的应用2 图解贝塞尔曲线3 贝塞尔曲线的性质4 算法仿真4.1 ROS C仿真4.2 Python仿真4.3 Matlab仿真 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法…...

【一万字干货】一篇给你讲清楚智慧城市——附送智慧系列开发项目合集
智慧城市的概念 智慧城市(Smart City)起源于传媒领域,是指利用各种信息技术或创新概念,将城市的系统和服务打通、集成,以提升资源运用的效率,优化城市管理和服务,以及改善市民生活质量。 中国…...

关于如何禁用、暂停或退出OneDrive等操作,看这篇文件就够了
想知道如何禁用OneDrive?你可以暂停OneDrive的文件同步,退出应用程序,阻止它在启动时打开,或者永远从你的机器上删除该应用程序。我们将向你展示如何在Windows计算机上完成所有这些操作。 如何在Windows上关闭OneDrive 有多种方法可以防止OneDrive在你的电脑上妨碍你。…...
Vue3-46-Pinia-获取全局状态变量的方式
使用说明 在 Pinia 中,获取状态变量的方式非常的简单 : 就和使用对象一样。 使用思路 : 1、导入Store;2、声明Store对象;3、使用对象。 在逻辑代码中使用 但是 Option Store 和 Setup Store 两种方式定义的全局状态变量…...

数据库——DAY1(Linux上安装MySQL8.0.35(网络仓库安装))
一、环境部署 1、Red Hat Enterprise Linux 9.3 64 位 2、删除之前安装过本地镜像版本的MySQL软件(以前未安装过,请跳过此步骤) [rootlocalhost ~]# dnf remove mysql-server -y [rootlocalhost ~]# rm -rf /var/lib/mysql [rootlocalhost …...
原生微信小程序-两次设置支付密码校验,密码设置二次确认
效果 具体代码 1、wxml <view style"{{themeColor}}"><view classcontainer><view class"password_content"><view wx:if{{type 1}}><view class"title"><view class"main_title">设置支付密码…...

【Python学习】Python学习15-模块
目录 【Python学习】Python学习15-模块 前言创建语法引入模块from…import 语句from…import* 语句搜索路径PYTHONPATH 变量-*- coding: UTF-8 -*-导入模块现在可以调用模块里包含的函数了PYTHONPATH 变量命名空间和作用域dir()函数globals() 和 locals() 函数reload() 函数Py…...
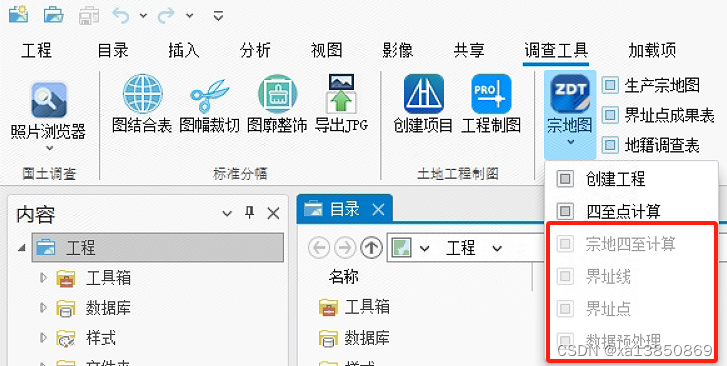
ARCGIS PRO SDK 设置UI控件状态:启用/禁用
举例: 第一步:添加两个 Button 分别命名为Connect、Disconnect 第二步:nfig.daml添加状态和条件:在 DAML 中定义条件。请记住,条件存在于模块标记<modules>之外,下代码定义:Disconnected_…...
案例126:基于微信小程序的民大食堂用餐综合服务平台
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...

cephfs 配置 mds stancd replay 操作
目的 1 假设有某个客户创建过千万文件目录,可以导致 ceph-mds 故障 2 backup ceph-mds 拉起时需要从内存中 replay 最后操作,可能需要吧当前目录中所有目> 录结构 重新 reload 至内存 3 这个过程可能需要几小时,可能需要几天 4 为了快速地拉起 ceph-mds 5 可以选择配置一…...

【2023我的编程之旅】系统学习C语言easyx图形库心得体会
目录 引言 C语言基础知识回顾 easyx图形库介绍 如何快速学习easyx图形库 学习笔记积累 学习成果展示 学习拓展 总结 引言 首先说一下我为什么要学习C语言easyx图形库。我接触C语言easyx图形库是在我今年一月份的时候,也是机缘巧合之下偶然在B站上看到了鸣人…...
【linux】软链接创建(linux的快捷方式创建)
软连接的概念 类似于windows系统中的快捷方式。有的文件目录很长或者每次使用都要找很不方便,于是可以用类似windows的快捷方式的软链接在home(初始目录类似于桌面)上创建一些软链接方便使用。 软链接的语法 ln -s 参数1 参数2 参数1&#…...

基于BP神经网络的光伏发电预测
目录 摘要 BP神经网络参数设置及各种函数选择 参数设置 训练函数 传递函数 学习函数 性能函数 显示函数 前向网络创建函数 BP神经网络训练窗口详解 训练窗口例样 训练窗口四部详解 基于BP神经网络的租金预测 代码下载:19-66天气预测光伏发电.rar(代码完整,数据齐全)资源-C…...
RPA财务机器人在厦门市海沧医院财务管理流程优化汇总的应用RPA全球生态 2024-01-05 17:27 发表于河北
目前国内外研究人员对于RPA机器人在财务管理流程优化领域中的应用研究层出不穷,但现有研究成果主要集中在财务业务单一领域,缺乏财务管理整体流程一体化管控的研究。RPA机器人的功能绝非单一的财务业务处理,无论从自身技术发展,或…...

应用在LCD显示器电源插头里的氮化镓(GaN)MTC-65W1C
LCD(Liquid Crystal Display)显示器是利用液晶显示技术来进行图像表现的显示装置,从液晶显示器的结构来看,无论是笔记本电脑还是桌面系统,采用的LCD显示屏都是由不同部分组成的分层结构。LCD显示器按照控制方式不同可分…...

Vue新手村(二)
目录 1、计算属性 2、事件修饰符 2.1、stop事件修饰符 2.2、prevent事件修饰符 2.3、self事件修饰符 2.4、once事件修饰符 3、按键修饰符 3.1、enter回车键 1、计算属性 计算属性: computed:vue官方提供一个计算属性作用:在完成某种业…...

Mysql-redoLog
Redo Log redo log进行刷盘的效率要远高于数据页刷盘,具体表现如下 redo log体积小,只记录了哪一页修改的内容,因此体积小,刷盘快 redo log是一直往末尾进行追加,属于顺序IO。效率显然比随机IO来的快Redo log 格式 在MySQL的InnoDB存储引擎中,redo log(重做日志)被用…...

编程笔记 html5cssjs 039 CSS背景示例
编程笔记 html5&css&js 039 CSS背景示例 一、html二、css小结 网页上只有三个水平并列大小相同的的DIV,大小为300p*200,如何使用CSS让它们整体水平和垂直都居中,并使用不同的背景色? 一、html 要在网页上实现三个水平并列且大小相同…...

沃尔玛如何通过安全、有效的测评补单提升产品权重?
在沃尔玛的众多卖家之中,如何让自己脱颖而出?这不仅需要我们提供具有竞争力的价格,更需要我们提升产品的评分和权重。要让更多的客户注意到我们的产品,补单测评或许是一种有效的策略。尤其在新品上架初期,由于缺乏好评…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
