快速排序、归并排序、希尔排序(2023-12-25)
参考文章 十大经典排序算法总结整理_十大排序算法-CSDN博客
推荐文章 算法:归并排序和快排的区别_归并排序和快速排序的区别-CSDN博客
package com.tarena.test.B20;
import java.util.Arrays;
import java.util.StringJoiner;
public class B25 {
static int num = 20;
static {
num = 10;
}
public static void main(String[] args) {
// num从准备到初始化值变化过程 num=0 -> num=20 -> num=10
// System.out.println(num);//10
Integer[] arr = new Integer[] { 15, 3, 2, 26, 38, 36, 50, 48, 47, 19, 44, 46, 27, 5, 4 };
print(arr);
// 快速排序
print(quickSort(Arrays.copyOf(arr, arr.length)));
// 归并排序
print("归并排序", mergeSort(Arrays.copyOf(arr, arr.length), 0, arr.length - 1));
// 希尔排序
print("希尔排序", grepSort(Arrays.copyOf(arr, arr.length)));
}
/**
* 快速排序 快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,
* 则可分别对这两部分记录继续进行排序,以达到整个序列有序。
*
* 4.1 算法描述
*
* 快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
*
* 从数列中挑出一个元素(通常选第一个元素),称为 “基准”(pivot);
* 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。
* 在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作; 对左右两个分区重复以上步骤直到所有元素都是有序的。
*
* @param arr
* @return
*/
public static Integer[] quickSort(Integer[] a) {
return quickSort(a, 0, a.length - 1);
}
public static Integer[] quickSort(Integer[] a, int _left_, int _right_) {
int left = _left_;
int right = _right_;
int temp = a[left]; // 每次把最左边的元素left当做基准,这里必须是left,注意!!!!
if (left >= right)
return a;
// 从左右两边交替扫描,直到left = right
while (left != right) {
while (right > left && a[right] >= temp)
right--; // 从右往左扫描,找到第一个比基准元素小的元素
a[left] = a[right]; // 找到后直接将a[right]赋值给a[l],赋值完之后a[right],有空位
while (left < right && a[left] <= temp)
left++; // 从左往右扫描,找到第一个比基准元素大的元素
a[right] = a[left]; // 找到这种元素arr[left]后,赋值给arr[right],上面说的空位。
}
a[left] = temp;
// 把基准插入,此时left与right已经相等
/* 拆分成两个数组 s[0,left-1]、s[left+1,n-1]又开始排序 */
quickSort(a, _left_, left - 1); // 对基准元素左边的元素进行递归排序
quickSort(a, right + 1, _right_); // 对基准元素右边的进行递归排序
return a;
}
/**
* 5、归并排序(Merge Sort) 相关文章:归并排序 - 简书
*
* 和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
*
* 归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and
* Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
*
* 5.1 算法描述
*
* 把长度为n的输入序列分成两个长度为n/2的子序列; 对这两个子序列分别采用归并排序; 将两个排序好的子序列合并成一个最终的排序序列。
*
* 下面一种是比较好理解的,原理如下(假设序列共有n个元素)
*
* 将原始序列从中间分为左、右两个子序列,此时序列数为2 将左序列和右序列再分别从中间分为左、右两个子序列,此时序列数为4
* 重复以上步骤,直到每个子序列都只有一个元素,可认为每一个子序列都是有序的 最后依次进行归并操作,直到序列数变为1
*
* 5. 4 算法分析
*
* 最佳情况:T(n) = O(n) 最差情况:T(n) = O(nlogn) 平均情况:T(n) = O(nlogn)
*
* @param a
*/
public static Integer[] mergeSort(Integer[] a, int left, int right) {
if (left >= right)
return a;
int center = (left + right) >> 1;
mergeSort(a, left, center);
mergeSort(a, center + 1, right);
merge(a, left, center, right);
return a;
}
public static void merge(Integer[] data, int left, int center, int right) {
int[] tmpArr = new int[right + 1];
int mid = center + 1;
int index = left; // index记录临时数组的索引
int tmp = left;
// 从两个数组中取出最小的放入中临时数组
while (left <= center && mid <= right) {
tmpArr[index++] = (data[left] <= data[mid]) ? data[left++] : data[mid++];
}
// 剩余部分依次放入临时数组
while (mid <= right) {
tmpArr[index++] = data[mid++];
}
while (left <= center) {
tmpArr[index++] = data[left++];
}
// 将临时数组中的内容复制回原数组
for (int i = tmp; i <= right; i++) {
data[i] = tmpArr[i];
}
// System.out.println(Arrays.toString(data));
}
/**
* 希尔排序
6、希尔排序(Shell Sort)
希尔排序是希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
希尔排序是把记录按下表的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
6.1 算法描述
我们来看下希尔排序的基本步骤,在此我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2...1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
按增量序列个数k,对序列进行k 趟排序;
每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
* @param name
* @param arr
*/
public static Integer[] grepSort(Integer[] array) {
int len = array.length;
if (len < 2) {
return array;
}
// 当前待排序数据,该数据之前的已被排序
int current;
// 增量
int gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
current = array[i];
// 前面有序序列的索引
int index = i - gap;
while (index >= 0 && current < array[index]) {
array[index + gap] = array[index];
// 有序序列的下一个
index -= gap;
}
// 插入
array[index + gap] = current;
}
// int相除取整
gap = gap / 2;
}
return array;
}
public static void print(String name, Integer[] arr) {
StringJoiner sj = new StringJoiner("-");
Arrays.stream(arr).forEach(num -> sj.add(String.valueOf(num)));
System.out.println(name + ":运行结果:" + sj.toString());
}
public static void print(Integer[] arr) {
StringJoiner sj = new StringJoiner("-");
Arrays.stream(arr).forEach(num -> sj.add(String.valueOf(num)));
System.out.println("运行结果:" + sj.toString());
}
}
了解知识点
1、复习一下三种基本的排序算法。
2、了解一下 static 属性字段的赋值过程。
相关文章:
)
快速排序、归并排序、希尔排序(2023-12-25)
参考文章 十大经典排序算法总结整理_十大排序算法-CSDN博客 推荐文章 算法:归并排序和快排的区别_归并排序和快速排序的区别-CSDN博客 package com.tarena.test.B20; import java.util.Arrays; import java.util.StringJoiner; public class B25 { static i…...

Qt SDL2播放Wav音频
这里介绍两种方法来实现Qt播放Wav音频数据。 方法一:使用QAudioOutput pro文件中加入multimedia模块。 #include <QApplication> #include <QFile> #include <QAudioFormat> #include <QAudioOutput>int main(int argc, char *argv[]) {…...
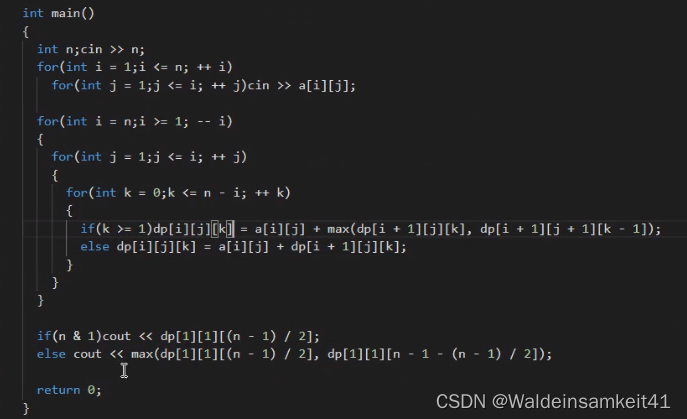
[ACM学习] 动态规划基础之一二三维dp
课内学习的动态规划 有记忆的迭代 优化解的结构:原始问题的一部分解是子问题的解 三要素:1.子问题 2.状态的定义 3.状态转移方程 定义 线性dp的一道例题 dp[i]表示以位置 i 结尾的方案总数,dp[4]2,因为:首先只放一…...

Qt点击按钮在其附近弹出一个窗口
效果 FS_PopupWidget.h #ifndef FS_POPUPWIDGET_H #define FS_POPUPWIDGET_H#pragma once#include <QToolButton> #include <QWidgetAction> #include <QPointer>class QMenu;class FS_PopupWidget : public QToolButton {Q_OBJECTpublic:FS_PopupWidget(QW…...

Springboot注解@Configuration和@Bean注解作用,生命周期
简介: Configuration 类是定义 bean 配置的地方,而 Bean 方法是具体创建 bean 实例的方法。 Configuration 作用: Configuration 注解用于定义配置类,表明该类包含一个或多个 bean 定义的方法。Spring 容器在启动时会自动扫描这些…...

30天精通Nodejs--第十五天:Websocket
引言 这里我们将继续深入探讨另一项强大且实时性极高的网络通信技术——WebSocket。通过本篇文章,将全面了解如何在Node.js环境中利用WebSocket实现服务端与客户端之间双向、低延迟的数据传输,并掌握其基础用法以及一些高级应用场景。 基础用法 安装WebSocket库 在Node.j…...

C++深入学习之STL:2、适配器、迭代器与算法部分
适配器概述 C标准模板库(STL)中提供了几种适配器,这些适配器主要用于修改或扩展容器类的功能。STL中的适配器主要包括以下几种: 1、迭代器适配器:迭代器适配器提供了一种机制,可以将非迭代器对象转换为迭代器对象。比如back_ins…...
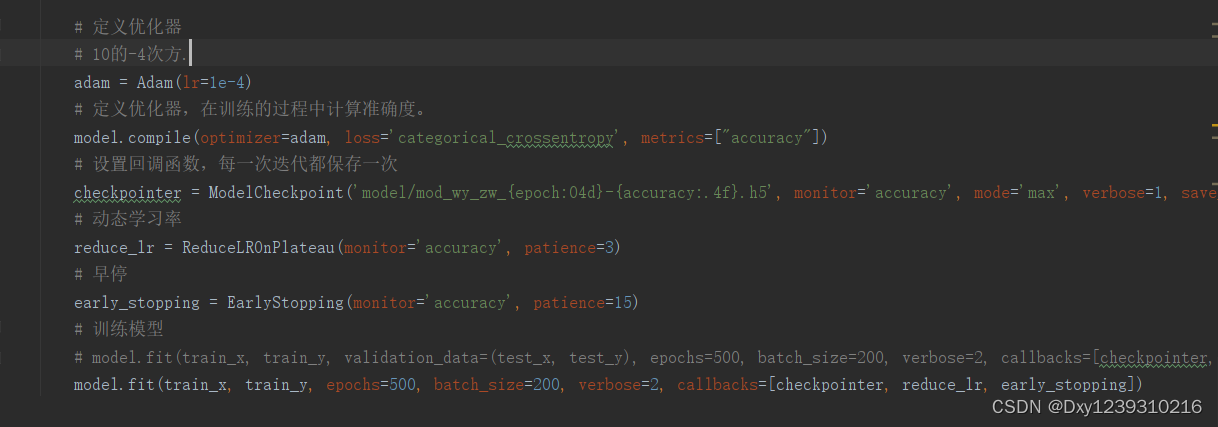
Tiktok/抖音旋转验证码识别
一、引言 在数字世界的飞速发展中,安全防护成为了一个不容忽视的课题。Tiktok/抖音,作为全球最大的短视频平台之一,每天都有数以亿计的用户活跃在其平台上。为了保护用户的账号安全,Tiktok/抖音引入了一种名为“旋转验证码”的安…...

【Java 设计模式】设计原则
文章目录 ✨单一职责原则(SRP)✨开放/封闭原则(OCP)✨里氏替换原则(LSP)✨依赖倒置原则(DIP)✨接口隔离原则(ISP)✨合成/聚合复用原则(CARP&#…...

Druid连接池工具公式化SQL附踩坑记录
1. 需求 使用Druid连接池工具格式化sql用于回显时候美观展示 2. 代码示例 2.1 依赖 <dependency><groupId>com.alibaba</groupId><artifactId>druid</artifactId><version>1.2.6</version> </dependency> 2.2 ParseUtils…...
UDP数据包发送)
Linux内核--网络协议栈(二)UDP数据包发送
目录 一、引言 二、数据包发送 ------>2.1、数据发送流程 三、协议层注册 ------>3.1、socket系统调用 ------>3.2、socket创建 ------>3.3、协议族初始化 ------>3.4、对应协议的socket创建 ------>3.5、协议注册 四、通过套接字发送网络数据 --…...
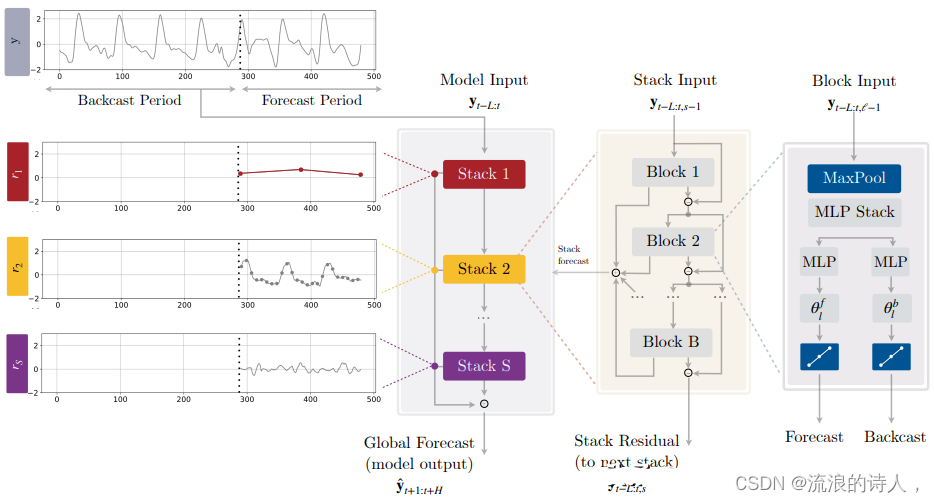
基于深度学习的时间序列算法总结
1.概述 深度学习方法是一种利用神经网络模型进行高级模式识别和自动特征提取的机器学习方法,近年来在时序预测领域取得了很好的成果。常用的深度学习模型包括循环神经网络(RNN)、长短时记忆网络(LSTM)、门控循环单元&a…...

nginx中多个server块共用upstream会相互影响吗
背景 nginx中经常有这样的场景,多个server块共用一个域名。 如:upstream有2个以上的域名,nginx配置两个server块,共用一个upstream配置。 那么,如果其中一个域名发生"no live upstreams while connecting to ups…...

基于信号完整性的一些PCB设计建议
最小化单根信号线质量的一些PCB设计建议 1. 使用受控阻抗线; 2. 理想情况下,所有信号都应该使用完整的电源或地平面作为其返回路径,关键信号则使用地平面作为返回路径; 3. 信号的返回参考面发生变化时,在尽可能接近…...
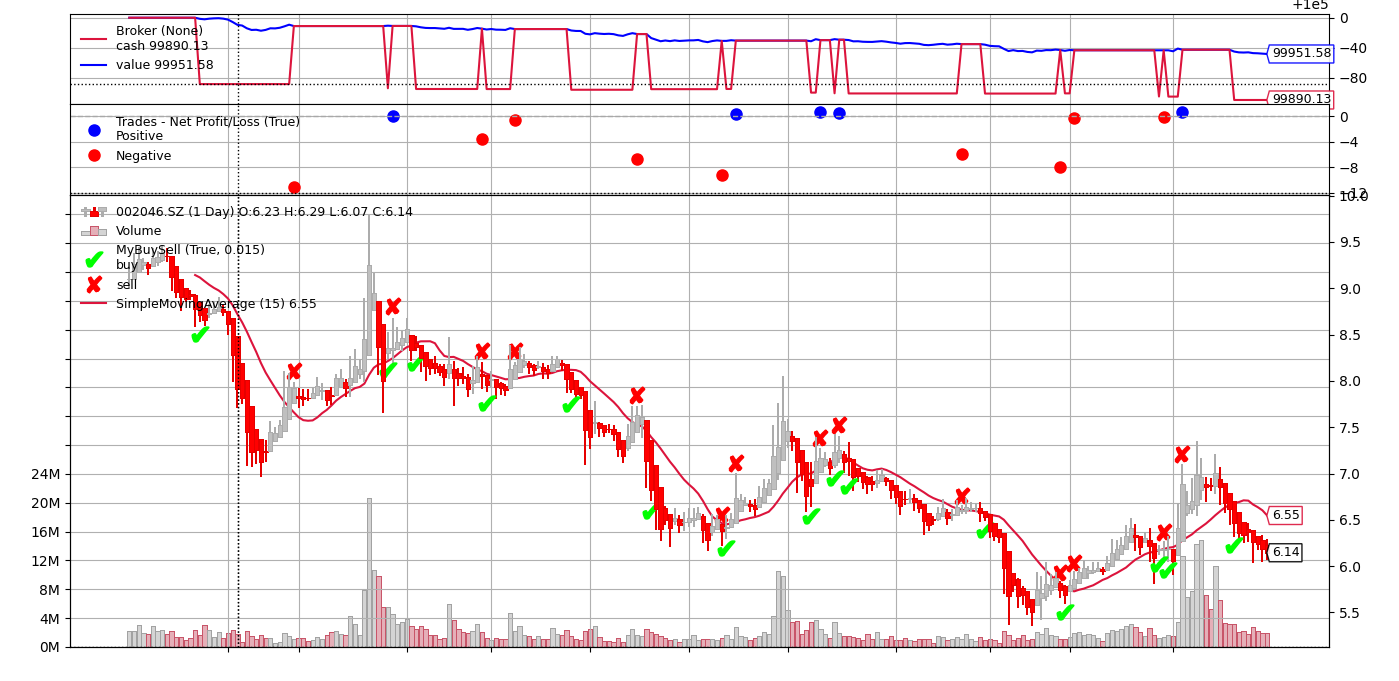
《BackTrader量化交易图解》第8章:plot 绘制金融图
文章目录 8. plot 绘制金融图8.1 金融分析曲线8.2 多曲线金融指标8.3 Observers 观测子模块8.4 plot 绘图函数的常用参数8.5 买卖点符号和色彩风格8.6 vol 成交参数8.7 多图拼接模式8.8 绘制 HA 平均 K 线图 8. plot 绘制金融图 8.1 金融分析曲线 BackTrader内置的plot绘图函…...

什么是欧拉筛??
欧拉筛(Eulers Sieve),又称线性筛法或欧拉线性筛,是一种高效筛选素数的方法。它的核心思想是从小到大遍历每个数,同时标记其倍数为合数,但每个合数只被其最小的质因数标记一次,从而避免了重复标…...
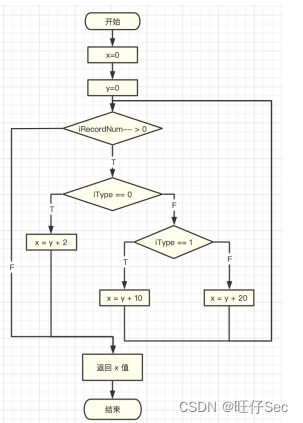
2023年全国职业院校技能大赛软件测试赛题—单元测试卷⑩
单元测试 一、任务要求 题目1:根据下列流程图编写程序实现相应处理,程序根据两个输入参数iRecordNum和IType计算x的值并返回。编写程序代码,使用JUnit框架编写测试类对编写的程序代码进行测试,测试类中设计最少的测试数据满足基路…...

使用WAF防御网络上的隐蔽威胁之SSRF攻击
服务器端请求伪造(SSRF)攻击是一种常见的网络安全威胁,它允许攻击者诱使服务器执行恶意请求。与跨站请求伪造(CSRF)相比,SSRF攻击针对的是服务器而不是用户。了解SSRF攻击的工作原理、如何防御它࿰…...
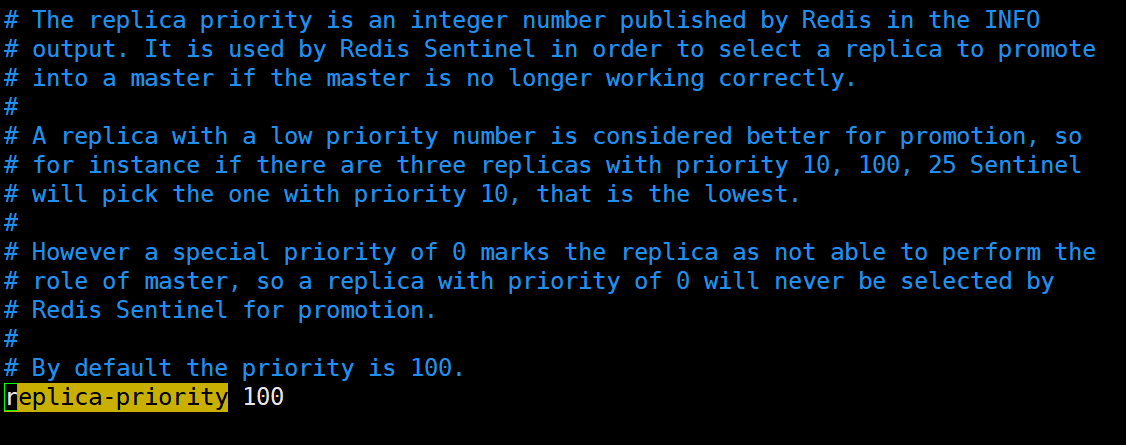
Redis基础系列-哨兵模式
Redis基础系列-哨兵模式 文章目录 Redis基础系列-哨兵模式1. 引言2. 什么是哨兵模式?3. 哨兵模式的配置4. 哨兵模式的启动和验证4.1 主master宕机,看会出现什么问题4.2 重启6379主机 5. 哨兵模式的工作原理和选举原理5.1. SDown主观下线(Subj…...
 Angular中的数据请求 与 路由)
【angular教程240112】09(完) Angular中的数据请求 与 路由
【angular教程240112】09(完) Angular中的数据请求 与 路由 目录标题 一、 Angular 请求数据简介0 使用Angular内置模块HttpClientModule和HttpClientJsonpModule:1 Angular中的GET请求:2 Angular中的POST请求:3 Angular中的JSONP请求:4使用Axios进行数据请求: 二、 详解 Angul…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
