动态规划Day06(完全背包)
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
同样leetcode上没有纯完全背包问题,都是需要完全背包的各种应用,需要转化成完全背包问题,所以我这里还是以纯完全背包问题进行讲解理论和原理。
每件物品可以放入多次
为什么遍历物品在外层循环,遍历背包容量在内层循环?
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
518.零钱兑换II(两次)
力扣题目链接(opens new window)
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
- 输入: amount = 5, coins = [1, 2, 5]
- 输出: 4
解释: 有四种方式可以凑成总金额:
- 5=5
- 5=2+2+1
- 5=2+1+1+1
- 5=1+1+1+1+1
看到题目的第一想法
确定可以凑成dp的组合数
但是相同面额的可以重复,使用完全背包
看到代码随想录之后的想法
确定dp数组以及每个下标的含义
dp[j] 为0~i之间能凑成j金额所需要的次数
i为coins下标
确定递推公式
选中coins[i] ,则一共有j-coins[i]种能凑成j
再加上本身的dp[j] ,就知道添加了coins[i]后一共要多少次
dp[j] = dp[j] + dp[j-coins[i]]
确定遍历顺序
可以重复添加物品,则从前往后
dp数组初始化
dp[0]=1为一切的源头,其他都为0
举例推导dp数组
自己实现过程中遇到的困难
我自己写成了 max(dp[j],dp[j-weight[i]]+1) 记混了
要理解组合数,求的是能凑成j的数目,需要累加j-coins[i]
class Solution {public int change(int amount, int[] coins) {//有多少种方式可以凑成对应面额// 确定dp数组以及每个下标的的含义// 能凑成目标金额的最大个数// 确定递推公式// dp[i]+=dp[i-nums[i]]// dp数组初始化// dp[0]=1;其他都为0// 确定遍历顺序// 从前往后,因为可以重复// 手动推导dp数组// 打印dp数组int dp[] = new int[amount+1];dp[0]=1;for(int i=0;i<coins.length;i++){//从前往后for(int j=coins[i];j<=amount;j++){dp[j]=dp[j]+dp[j-coins[i]];}}return dp[amount];}
}377. 组合总和 Ⅳ
力扣题目链接(opens new window)
难度:中等
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
- nums = [1, 2, 3]
- target = 4
所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
看到题目的第一想法
可以凑成目标正整数的组合的个数。
和零钱兑换II差不多
看到代码随想录之后的想法
确定dp数组以及每个下标的含义
dp[j] 为0~i之间能凑成target所需要的次数
i为nums下标
确定递推公式
选中nums[i] ,则一共有j-nums[i]种能凑成j
再加上本身的dp[j] ,就知道添加了nums[i]后一共要多少次
dp[j] = dp[j] + dp[j-nums[i]]
确定遍历顺序
可以重复添加物品,则从前往后
比如说 (1231) 若可以凑成target
如果先物品后背包 物品1 遍历完后 ,将再也不会遍历到1,之后遍历的是物品2,3,4
所以必须先背包后物品
外层循环是背包容量,物品按照 1 2 3 4的顺序,依次遍历 则 遍历完1,2,3还能遍历回1
dp数组初始化
dp[0]=1为一切的源头,其他都为0
举例推导dp数组
自己实现过程中遇到的困难
需要确认组合数和排列数的区别(看代码注释)
组合数: 不强调顺序,不同顺序的都视为一个集合,必须先物品再背包
排列数: 本题不同的地方在于不同顺序的视为不同集合,则必须先背包再物品
class Solution {public int combinationSum4(int[] nums, int target) {// 组合数:先遍历物品再遍历背包:每次选中一个物品都会遍历所有背包 1号物品一定在2号物品的前面// 排列数:先遍历背包再遍历物品:则每次选中一个背包都会遍历所有物品 每次都是 1号物品,2号物品。。。。 // 第二次 1号物品2号物品 1 2 交替 // 确定dp数组,以及对应下标的含义// 在0~i中满足总和为j的元素的个数,背包重量nums[i] 背包价值nums[i]// 确定递推公式// dp[j]+=dp[j-nums[i]]// dp数组的初始化// dp[0]=1 // 确定遍历顺序// 可以重复 从前往后// 组合数: 不强调顺序,不同顺序的都视为一个集合,必须先物品再背包// 排列数: 本题不同的地方在于不同顺序的视为不同集合,则必须先背包再物品// 手动推导dp数组int[] dp = new int[target+1];dp[0]=1;for(int j=0;j<=target;j++){for(int i=0;i<nums.length;i++){if(j>=nums[i]){dp[j]+=dp[j-nums[i]];}}}return dp[target];}
}相关文章:
)
动态规划Day06(完全背包)
完全背包 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。 完全背包和01背包问题唯一不同…...
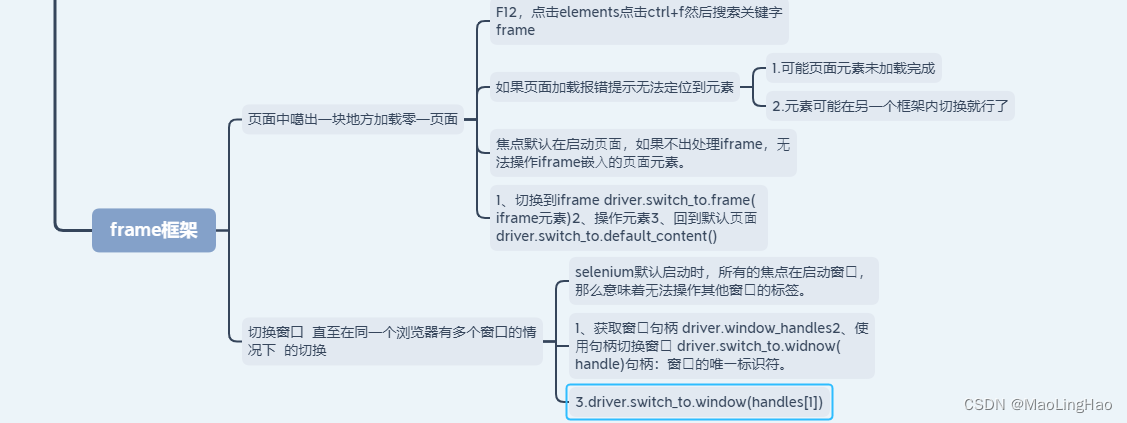
selenium之框架之窗口
...
)
华为OD机试 - 最小矩阵宽度(Java JS Python C)
题目描述 给定一个矩阵,包含 N * M 个整数,和一个包含 K 个整数的数组。 现在要求在这个矩阵中找一个宽度最小的子矩阵,要求子矩阵包含数组中所有的整数。 输入描述 第一行输入两个正整数 N,M,表示矩阵大小。 接下来 N 行 M 列表示矩阵内容。 下一行包含一个正整数 K…...

嵌入式linux_C应用学习之API函数
1.文件IO 1.1 open打开文件 #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> int open(const char *pathname, int flags); int open(const char *pathname, int flags, mode_t mode);pathname:字符串类型,用于标…...
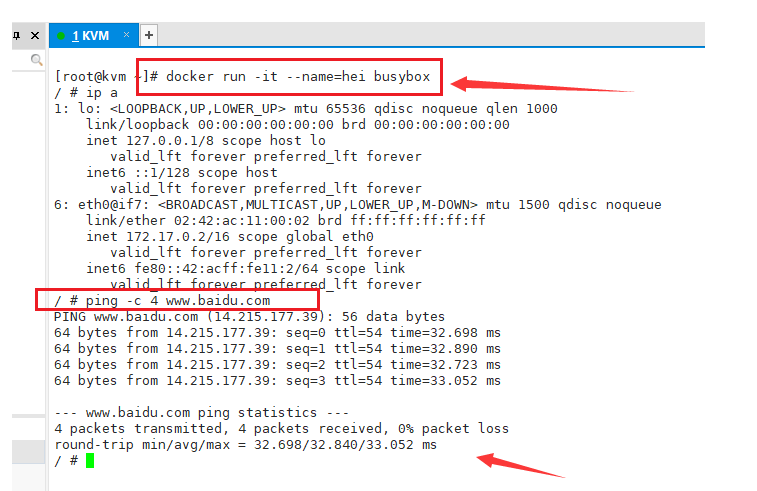
【ubuntu】docker中如何ping其他ip或外网
docker中如何ping其他ip或外网 示例图: 运行下面命令: docker run -it --namehei busybox看情况需要加权限 sudo,即: sudo docker run -it --namehei busyboxping 外网 ping -c 4 www.baidu.comping 内网 ping -c 4 192.168.…...

【Vue3+Ts项目】硅谷甄选 — 品牌管理+平台属性管理+SPU管理+SKU管理
一、品牌管理模块 1.1 静态模块搭建 使用到element-plus的card、button、table、pagination等组件:src/views/product/trademark/index.vue <template><el-card><!-- 卡片顶部添加品牌按钮 --><el-button type"primary" size&quo…...

计算机图形学流体模拟 blender 渲染脚本
做流体模拟的时候,想要复现别人的成果,但是别人的代码都是每帧输出 ply 格式的文件,渲染部分需要自己完成 看了一下,似乎用 blender 是最简单的,于是记录一下过程中用到的代码 Blender 版本 4.0 批量导入 ply 假设…...
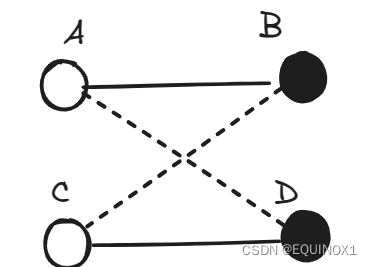
二分图带权最大匹配-KM算法详解
文章目录 零、前言一、红娘再牵线二、二分图带权最大完备匹配2.1二分图带权最大匹配2.2概念2.3KM算法2.3.1交错树2.3.2顶标2.3.3相等子图2.3.4算法原理2.3.5算法实现 三、OJ练习3.1奔小康赚大钱3.2Ants 零、前言 关于二分图:二分图及染色法判定-CSDN博客 关于二分…...

Redis命令 - Sets命令组常用命令
Set集合,无序,一堆不重复值的组合。利用redis提供的set数据结构,可以存储一些集合性的数据。 使用场景:例如,实现如共同关注、共同喜好、二度好友等 1、SADD key member [member …] 向集合中添加一个或者多个成员 …...

DA14531-外设驱动篇-I2C通信应用
文章目录 1.I2C通信应用相关文件2.宏定义列表3.主要函数接口4.应用代码实例1.I2C通信应用相关文件 1)i2c.c和i2c.h(SDK文件) 2)app_I2cProtocol.c和app_I2cProtocol.h(用户应用文件) 2.宏定义列表 宏定义注解I2C_ADDRESSING_7B7-bit 地址I2C_ADDRESSING_10B10-bit 地址…...

Git仓库管理笔记
问题: hint: the same ref. If you want to integrate the remote changes, use Done 解决: 解决方法: 1、先使用pull命令: git pull --rebase origin master 2、再使用push命令: git push -u origin master...
[嵌入式软件][入门篇] 搭建在线仿真平台(STM32)
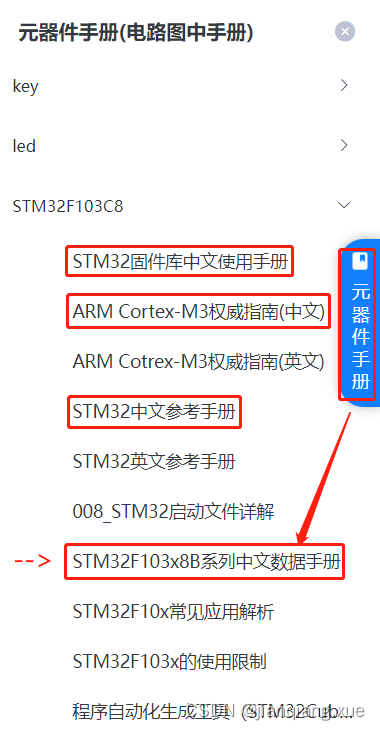
文章目录 一、注册平台二、创建首个项目三、硬件介绍 一、注册平台 进入官方,进行注册: 在线仿真地址 二、创建首个项目 ① 新建项目 ② 搭建一个电路 ③ 用STM32F103搭建一个简单电路 ④ 进入编码界面 三、硬件介绍 红框是必看文档ÿ…...

设置5台SSH互免的虚拟机服务器配置
搭建一套集群虚拟机,往往都需要互免设置,过程很简单,避免以后再搭建还得网上搜索,我直接将这一个步骤写成笔记,记录下来,方便后续查阅。 步骤如下—— 1、准备五台机器 服务器名字服务器IPhadoop1192.16…...

深信服技术认证“SCCA-C”划重点:交付和运维体系
为帮助大家更加系统化地学习云计算知识,高效通过云计算工程师认证,深信服特推出“SCCA-C认证备考秘笈”,共十期内容。“考试重点”内容框架,帮助大家快速get重点知识。 划重点来啦 *点击图片放大展示 深信服云计算认证ÿ…...
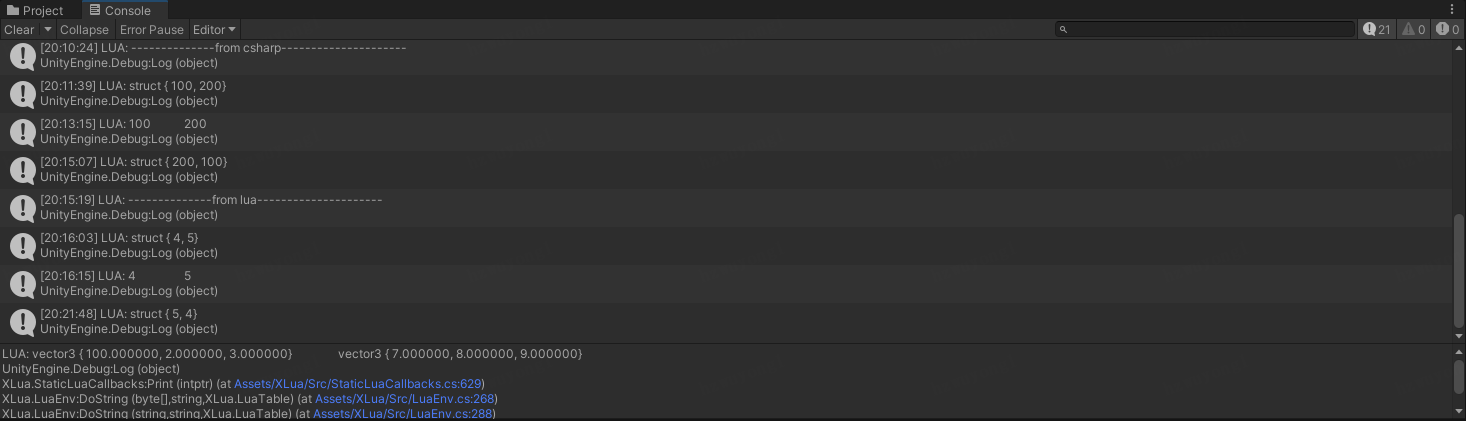
xlua源码分析(五) struct类型优化
xlua源码分析(五) struct类型优化 上一节我们分析了xlua是如何实现lua层访问C#值类型的,其中我们重点提到了xlua默认实现方式下,struct访问的效率问题。实际上,xlua还提供了两种优化的方式,可以大大提高str…...

iptables TEE模块测试小记
概述 因为公司项目需求,需要对服务器特定端口进行流量镜像,各种百度之后,发现TEE的模块,后来一番折腾,发现被转发的机器死活收不到数据,最后tcpdump一通了解到根源,博文记录,用以备…...

facebook广告怎么设置受众人群
在设置Facebook广告受众人群时,你可以遵循以下步骤: 打开广告创建工具,点击页面右上角的箭头并选择“创建广告”。选择广告目标,根据想要实现的目标创建广告。例如,想要让更多用户谈论你的主页和帖子,或者…...

MySQL夯实之路-MVCC机制深入浅出
多版本并发控制(MVCC,multiversion concurrency control) MVCC用更加灵活的方式处理并发,实现了读不加锁,读写不冲突。保证了事务的隔离性(可重复读),避免了不可重复读问题。 数据…...
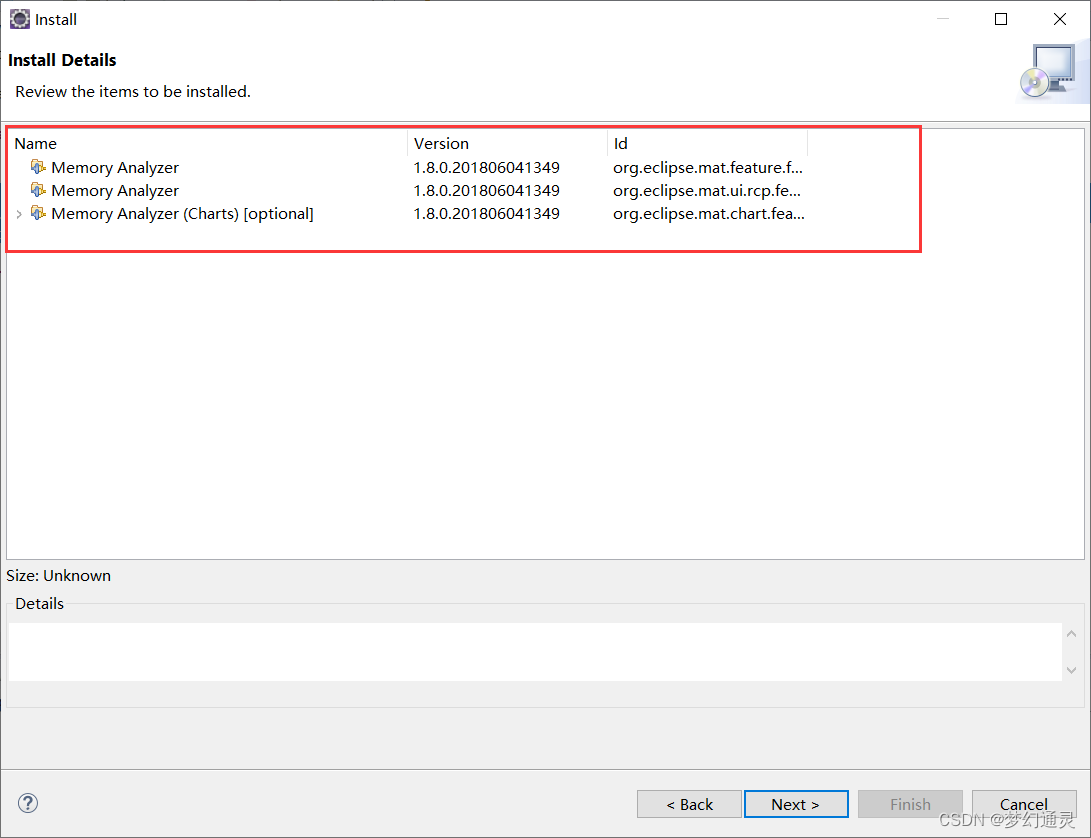
Java线上问题堆栈排查分析
最近线上出现类似内存溢出问题,需要排查具体原因,记录过程,方便备查。 一、数据抓取 在启动参数中添加参数,可参照以下设置。 参数的作用是在程序发生内存溢出 OutOfMemory 时打印日志,dump下来,方便用工…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...