qt.qpa.plugin: Could not find the Qt platform plugin “windows“ in ““
系统环境：Win10家庭中文版
Qt : 5.12.9
链接了一些64位的第三方库，程序编译完运行后出现
qt.qpa.plugin: Could not find the Qt platform plugin "windows" in ""
弹窗如下：
网上搜了一些都是关于pyQt的，最终临时解决方案如下：
将Windows下打包发布的platforms文件夹拷贝到可执行程序目录。
Windows下打包发布链接：Windows下打包发布程序
platforms文件夹内容如下：
相关文章：
qt.qpa.plugin: Could not find the Qt platform plugin “windows“ in ““
系统环境：Win10家庭中文版 Qt : 5.12.9 链接了一些64位的第三方库，程序编译完运行后出现 qt.qpa.plugin: Could not find the Qt platform plugin "windows" in "" 弹窗如下： 网上搜了一些都是关于pyQt的，…...
vue面试题集锦
1. 谈一谈对 MVVM 的理解？ MVVM 是 Model-View-ViewModel 的缩写。MVVM 是一种设计思想。 Model 层代表数据模型，也可以在 Model 中定义数据修改和操作的业务逻辑; View 代表 UI 组件，它负责将数据模型转化成 UI 展现出来，View 是…...
2024年学鸿蒙开发就业前景怎么样？
随着科技的不断进步，鸿蒙系统作为华为自主研发的操作系统，逐渐引起了人们的关注。 2024年，鸿蒙开发就业前景如何？ 对于那些对鸿蒙开发感兴趣并希望在这一领域寻找职业发展的人来说，这是一个非常重要的问题。 首先&a…...
Unity网络通讯学习
---部分截图来自 siki学院Unity网络通讯课程 Socket 网络上的两个程序通过一个双向的通信连接实现数据交换，这个连接的一端称为一个 Socket ，Socket 包含了网络通信必须的五种信息 Socket 例子{ 协议： TCP 本地： IP ÿ…...
js入口函数和jQuery入口函数的区别
JS入口函数指的是JavaScript中的主入口函数，用来初始化页面加载完成后的操作。通常情况下，JS入口函数是在HTML页面中的<script>标签中定义的，通过onload事件等方式触发调用。 jQuery入口函数则是指使用jQuery库时的主入口函数…...
Docker-Compose编排Nginx1.25.1+PHP7.4.33+Redis7.0.11环境
实践说明：基于RHEL7(CentOS7.9)部署docker环境(23.0.1、24.0.2)，编排也可应用于RHEL7-9(如AlmaLinux9.1)，但因为docker的特性，适用场景是不限于此的。 文档形成时期：2017-2023年 因系统或软件版本不同，构建…...
《新课程教学》（电子版）是正规期刊吗？能评职称吗？
《新课程教学》（电子版）主要出版内容为学科教学理论、学科教学实践经验和成果，主要读者对象为中小学教师，期刊设卷首语、名家讲堂、课程与教学、教学实践、考试评价、教育信息化、教学琐谈、教育管理、教师心语、一线课堂、重温经…...
Posgresql macOS安装和基础操作
摘要 本文介绍macOS版本Postgresql的安装，pg常用命令。作为笔记记录，后续方便查看。 Postgresql安装 官网下载postgresql安装包https://www.postgresql.org/download/。官网下载慢时，可以从这里下载我上传的mac版本的pg安装包资源。下载后&am…...
ArkUI-X跨平台已至，何需其它！
运行环境 DevEco Studio：4.0Release OpenHarmony SDK API10 开发板：润和DAYU200 自从写了一篇ArkUI-X跨平台的文章之后，好多人都说对这个项目十分关注。 那么今天我们就来完整的梳理一下这个项目。 1、ArkUI-X 我们之前可能更多接触的…...
（2024，分数蒸馏抽样，Delta 降噪分数，LoRA）PALP：文本到图像模型的提示对齐个性化
PALP: Prompt Aligned Personalization of Text-to-Image Models 公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群） 目录 0. 摘要 4. 提示对齐方法 4.1 概述 4.2 个性化 4.3 提示对齐分数抽…...
近日遇到数据库及其他问题
一、查找备份表和原表不一样数据 select * from A where (select count(1) from A_BAK where A.IDA_BAK.ID) 0 二、在数据量比较大的表中新增有默认值的列速度较慢问题 使用 以下语句，在上亿数据的表中执行速度较慢 alter table TEST add col_a integer DEFA…...
【conda】conda 版本控制和环境迁移/安装conda加速工具mamba /conda常用指令/Anaconda配置
【conda】安装conda加速工具mamba /conda常用指令/Anaconda配置 0. conda 版本控制和环境迁移1. 安装conda加速工具mamba2. conda install version3. [Anaconda 镜像](https://mirrors.tuna.tsinghua.edu.cn/help/anaconda/)使用帮助4. error deal 0. conda 版本控制和环境迁移…...
“/bin/bash“: stat /bin/bash: no such file or directory: unknown
简介：常规情况下，在进入容器时习惯使用 /bin/bash为结尾，如：docker exec -it test-sanic /bin/bash， 但是如果容器本身使用了精简版，只装了sh命令，未安装bash。这时就会抛出"/bin/bash&quo…...
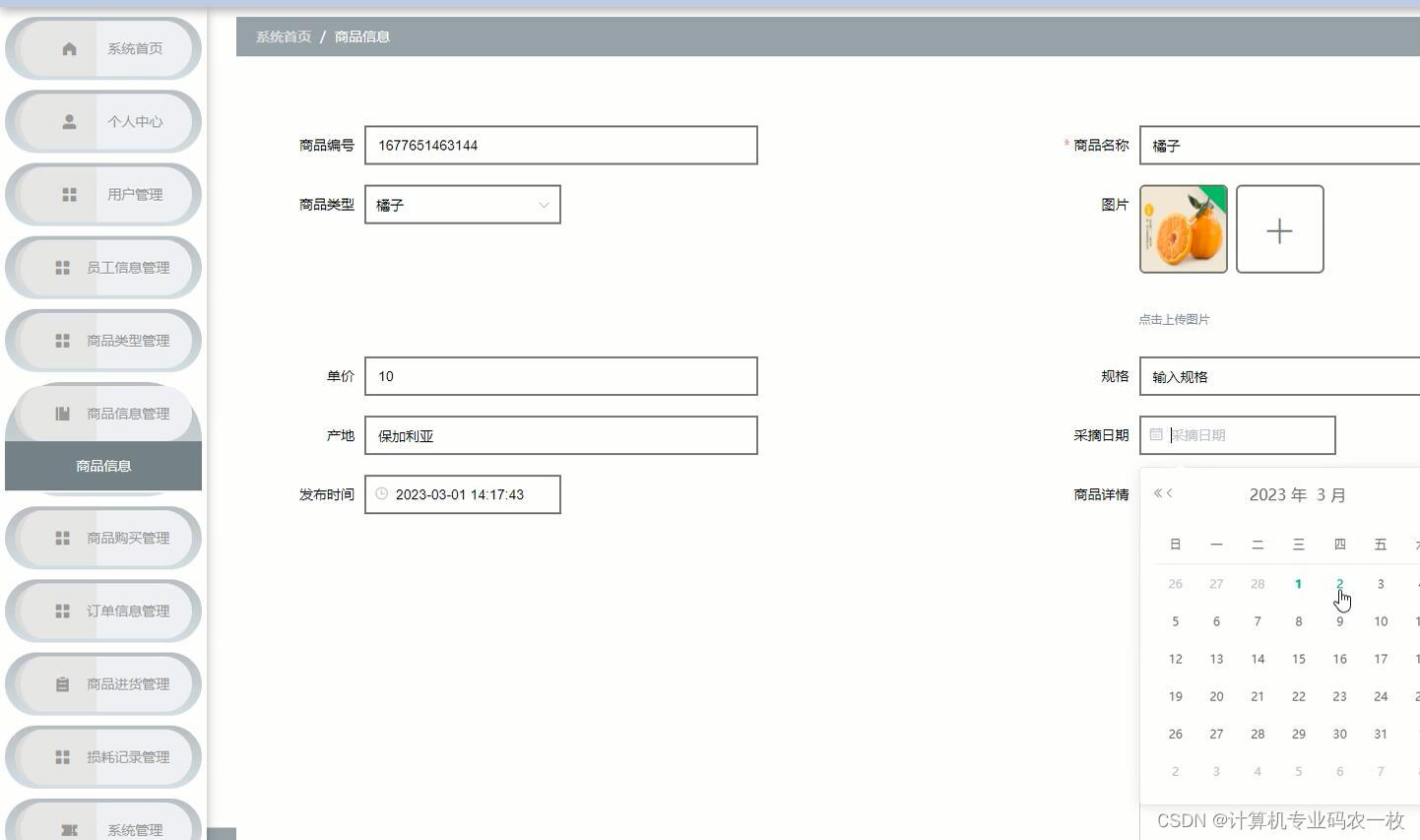
基于Spring Boot+vue的云上新鲜水果超市商城系统
本云上水果超市是为了提高用户查阅信息的效率和管理人员管理信息的工作效率，可以快速存储大量数据，还有信息检索功能，这大大的满足了用户、员工信息和管理员这三者的需求。操作简单易懂，合理分析各个模块的功能，尽可能…...
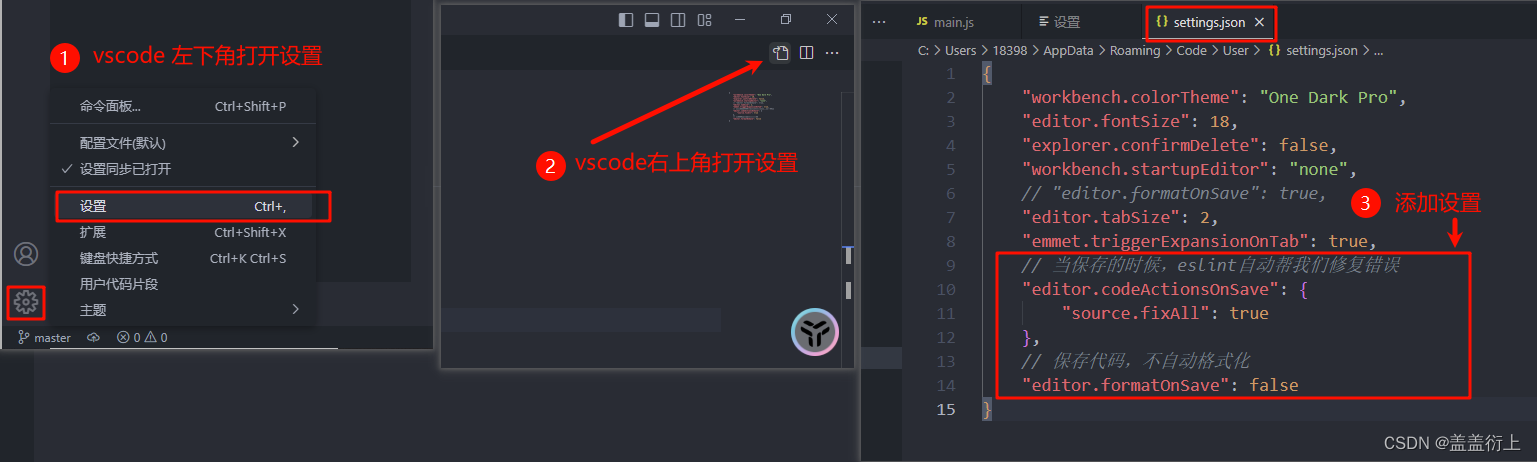
vue-ESlint代码规范及修复
1. 介绍 ESLint:是一个代码检查工具，用来检查你的代码是否符合指定的规则(你和你的团队可以自行约定一套规则)。 在创建项目时，我们使用的是 JavaScript Standard Style 代码风格的规则。 规范网址：https://standardjs.com/rules-zhcn.htm…...
Oracle数据库断电后不能打开的解决
数据库突然断电后，不能打开。或者偶尔能打开，但是很快就关闭。 原因可能很多。但是解决问题只有一种办法：看trace日志，alert错误日志 简单写下我的解决过程： 1,在alert日志中： 错误如下两种：…...
论文复现： In-Loop Filter with Customized Weights For VVC Intra Coding
论文复现： In-Loop Filter with Customized Weights For VVC Intra Coding 这个好难好难。啊啊啊啊。核心：权重预测模块功能快捷键合理的创建标题，有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的…...
配置华为设备NQA UDP Jitter检测VoIP业务抖动
组网需求 如图1所示，总部和子公司之间需要跨越外部网络进行通信，DeviceA和DeviceD为总部和子公司的网络出口设备，DeviceB和DeviceC为外部网络提供商的边缘设备。 总部和子公司之间经常要通过VoIP进行电话会议，要求双向时延小于2…...
GitHub要求所有贡献代码的用户在2023年底前启用双因素认证
到2023年底，所有向github托管的存储库贡献代码的用户都必须启用一种或多种形式的2FA。 双重身份认证 所谓双重身份认证（Two-Factor Authentication），就是在账号密码以外还额外需要一种方式来确认用户身份。 GitHub正在大力推动双…...
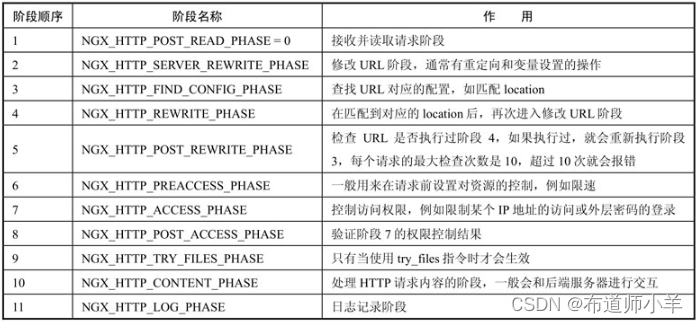
Nginx——强化基础配置
1、牢记Context Context是Nginx中每条指令都会附带的信息，用来说明指令在哪个指令块中使用，可以将Context 理解为配置环境。 每个指令都拥有自己的配置环境，如果把配置环境记错了，或者在设计时未考虑配置环境的作用，…...
visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中，选择 环境 -> 常规 ，将其中的颜色主题改成深色 点击确定，更改完成...
定时器任务——若依源码分析
分析util包下面的工具类schedule utils： ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类，封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz，先构建任务的 JobD…...
工程地质软件市场：发展现状、趋势与策略建议
一、引言 在工程建设领域，准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具，正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2（Navigation2）的行为树框架中，行为树节点插件按照功能分为 Action（动作节点）、Condition（条件节点）、Control（控制节点） 和 Decorator（装饰节点） 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务，直接与硬件、传感器或外部系统…...
Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统，支持多语言对话（如 中文，英文，日语），语音情感（如 开心，悲伤）&#x…...
重启Eureka集群中的节点，对已经注册的服务有什么影响
先看答案，如果正确地操作，重启Eureka集群中的节点，对已经注册的服务影响非常小，甚至可以做到无感知。 但如果操作不当，可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化（Gradient Normalization） (2) 判别器梯度间隙正则化（Discriminator Gradient Gap Regularization） (3) 自注意力机制（Self-Attention） 3. 完整损失函数 二…...
Bean 作用域有哪些？如何答出技术深度？
导语： Spring 面试绕不开 Bean 的作用域问题，这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开，结合典型面试题及实战场景，帮你厘清重点，打破模板式回答，…...
Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强：基于微服务与容器化的解决方案
在大数据时代，海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构，在处理大规模数据抓取任务时展现出强大的能力。然而，随着业务规模的不断扩大和数据抓取需求的日益复杂，传统…...
链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好，我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题，统一使用 二重复合函数： z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式（偏导…...