矩阵行列式的四大应用
目录
一. 介绍
二. 行列式的基本性质
2.1 单位阵的行列式
2.2 交换行位置的行列式
三. 矩阵求逆与行列式
四. 体积与行列式
五. 矩阵主元与行列式
六. 解方程与矩阵行列式
七. 小结
一. 介绍
行列式可以反应矩阵的很多性质,比如可以求矩阵的逆,也可以求方程的解,如下:
矩阵行列式有三个基础的性质:
(1)单位阵
单位阵的行列式为1,也就是:
det I=1
(2) 符号
矩阵的行位置交换会影响行列式的符号
(3)线性关系
矩阵行列式与行向量之间呈现线性关系
本文章将梳理矩阵行列式的四个基本应用。
二. 行列式的基本性质
以2行2列的矩阵为例,其行列式的计算非常简单,如下:
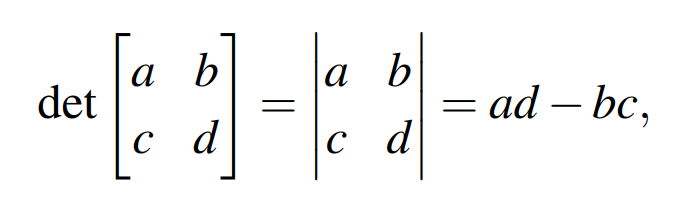
通常行列式有两种常用写法,分别是detA和|A|
以下我们将主要讨论方阵。
2.1 单位阵的行列式
很明显单位矩阵(identity matrix)的行列式为1,如下:

2.2 交换行位置的行列式
当把某两行的位置交换时,行列式会改变符号,如下:

任何置换矩阵都可以变成单位阵,单位阵的行列式为1,由此可得置换矩阵的行列式只能取1或-1,如下:
三. 矩阵求逆与行列式
我们都知道如果矩阵行列式为0时,那么其为奇异矩阵(singular)。如果矩阵A行列式不为0,那么该矩阵可以直接求逆,如下:
逆矩阵中的元素与行列式的倒数相关。
在求矩阵特征值时,涉及到:
其中的值会出现在矩阵对角线上,要保证该方程有解,那么要求
是奇异的,也就是可得:
把以上等式看成一个方程,如果该方程为n次方,也就是有n个解,从而矩阵A有n个特征值。
四. 体积与行列式
以最简单的三维立方体为例子dV=dxdydz,也就是:
如果写成柱坐标(cylindrical coordinates),可得:
dx的积分运算替换成(dx/du)du,由此可得体积运算为:
于是,雅克比行列式(Jacobian determinant)就可以写成三维的形式,如下:

此三阶矩阵的行列式很容易计算为r
综上可得矩阵A的行列式与n维箱子的体积相等,在网络安全中此结论是很有用的,来看一个直观的图形:
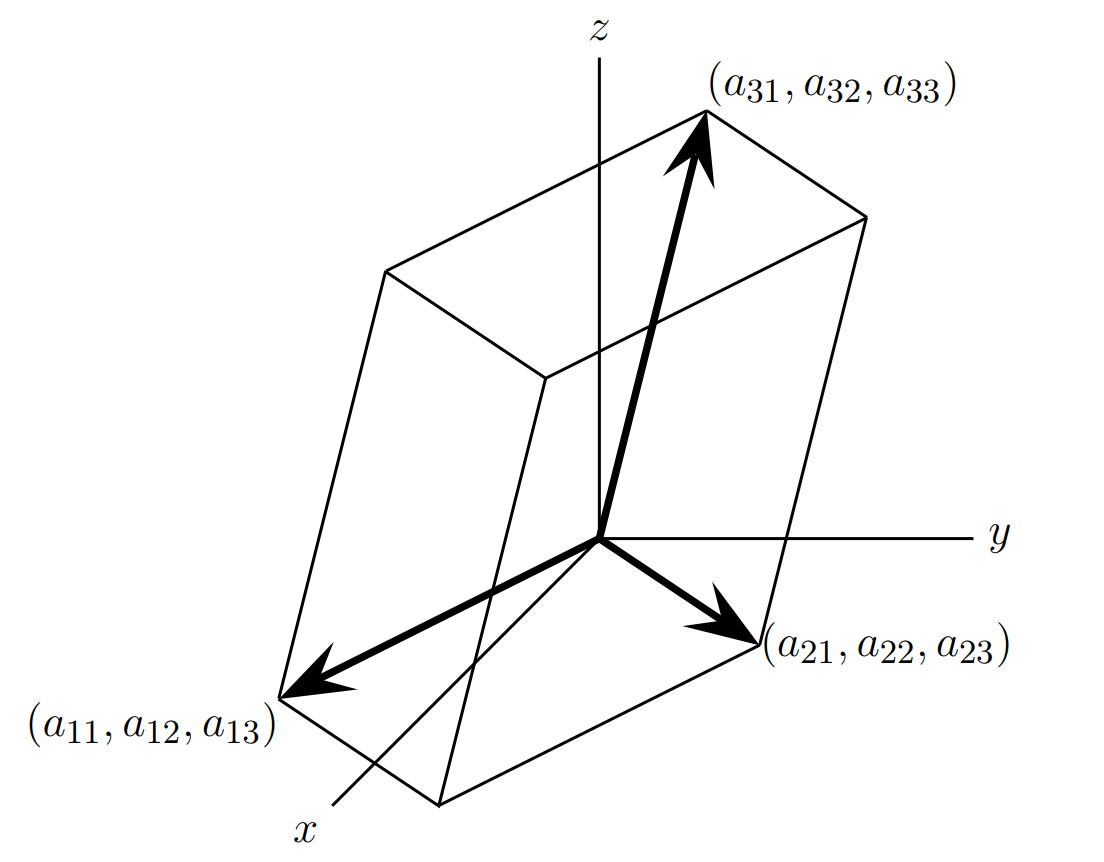
五. 矩阵主元与行列式
忽略正负号的情况下,矩阵行列式等于矩阵主元(pivots)的乘积。
六. 解方程与矩阵行列式
可以用行列式的思想来衡量b对的影响。利用行列式可以直接计算矩阵A的逆,接着利用Cramer法则计算解:
七. 小结
以上讨论中,我们了解到行列式的值与主元的乘积相关。通常而言计算行列式有两个常用的公式,一个是所谓的big formula,另外一个是 formula by induction。
(1)线性代数需要掌握的重点
行列式 内容:行列式的定义和性质;Cramer 法则;子式与代数余子式;按一行(列)展开定理。
要求: 掌握行列式的概念和性质,熟练应用行列式的性质计算行列式,并会用行列式求解线性方程组。
矩阵及其运算、矩阵的初等变换与线性方程组 内容: 矩阵的概念和运算;常用的特殊矩阵;矩阵的初等变换与初等矩阵;可逆矩阵以及性质 ;矩阵的秩等概念。 线性方程组的解。
要求: 掌握矩阵和秩的概念;能熟练地进行矩阵的各种运算(加、减、数乘、乘、求逆等);会求逆阵和矩阵的秩。
向量组的线性相关性 内容: 向量组及其线性组合、向量组的线性相关性,向量组的秩,线性方程组的解的结构,向量空间。
要求: 掌握向量的线性关系(组合与等价、线性相关与线性无关、极大线性无关组)等概念, 能熟练应用矩阵来求解或讨论线性方程组的解和解的结构。掌握向量空间的有关知识。
(2)矩阵应用
随着计算机硬件的发展和处理复杂算法能力的提高 ,近30年来 ,以人工智能为核心的相关学科群 :计算机视觉 、模式识别(含机器学习) 、数字图像处理 、数字信号处理和计算机图形学得到了迅速的发展 .20世纪90年代 ,这些学科的发展逐步走向成熟 ,相关技术的融合和实际应用显著增长 .而且 ,随着计算机应用深入到社会科学和生物学等学科 ,加之计算机网络的迅速扩展 ,数据的维数激增和数据量按指数增长 ,计算机所处理的数据发生了根本性的变化 ,这些都将进一步推动相关学科向纵深发展 . 在这些学科研究的过程中 ,涉及数学知识的广度和深度都超出了人们的想象 .
在广度上 ,几乎所有数学科目都在这些学科的研究中出现过 ,而不像传统的学科 , 如物理主要应用微分几何 、偏微分方程和群论 ;不仅如此 ,这些学科研究过程中所用的数学理论往往是当前数学界最新的研究成果 ,比如图像处理中所用的偏微分方程理论 .这对没有受过严格数学训练的计算机学者提出了严峻挑战 . 传统的计算机学科研究所用到的数学主要集中在离散数学 、算法设计 、数值计算和组合数学 ,这些19世纪的数学已经无法满足当前计算机科学发展的要求 .为此 ,众多的计算机学者一方面呼吁数学工作者加入到计算机科学的研究中 ,同时也积极地将相关的数学理论引入到研究中。
矩阵计算又称为数值线性代数 .作为一门数学学科 ,它是众多理工学科重要的数学工具 .矩阵理论既是经典数学的基础课程 ,是一门最有实用价值的数学理论 ,是计算机科学与工程计算的核心 ,已成为现代各科技领域处理大量有限维空间形式与数量关系强有力的工具 ,计算机科学和工程的问题最终都转化成矩阵的运算与求解 .特别是计算机的广泛应用为矩阵论的应用开辟了广阔的前景 .例如 ,系统工程 、优化方法以及稳定性理论等 ,都与矩阵论有着密切的联系。
相关文章:
矩阵行列式的四大应用
目录 一. 介绍 二. 行列式的基本性质 2.1 单位阵的行列式 2.2 交换行位置的行列式 三. 矩阵求逆与行列式 四. 体积与行列式 五. 矩阵主元与行列式 六. 解方程与矩阵行列式 七. 小结 一. 介绍 行列式可以反应矩阵的很多性质,比如可以求矩阵的逆,…...

【小笔记】时序数据分类算法最新小结
2024.1.15 最近基于时序数据训练分类算法,对其进行了一番了解,主要围绕以下几点: 时序数据算法有哪些细分类?时序数据分类算法经典模型?当下时序分类算法模型强baseline?有没有现成的工具? 1…...
使用Python+pygame实现贪吃蛇小游戏
使用Pythonpygame贪吃蛇小游戏 使用第三方库pygame,关于Python中pygame游戏模块的安装使用可见 https://blog.csdn.net/cnds123/article/details/119514520 给出两种实现。 第一种 运行效果如下: 游戏源码如下: import pygame import sy…...

SpringBoot 全局异常统一处理:BindException(绑定异常)
概述 在Spring Boot应用中,数据绑定是一个至关重要的环节,它负责将HTTP请求中的参数映射到控制器方法的入参对象上。在这个过程中如果遇到任何问题,如参数缺失、类型不匹配或验证失败等,Spring MVC将会抛出一个org.springframewo…...

ucloud轻量云(wordpress)配置ssl
ucloud 轻量云(wordpress)配置ssl 1、上传ssl证书到/usr/local/software/apache/conf,这里的文件名和内容与ucloud控制台下载下来的文件名和内容保持一致 2、修改httpd.conf文件 vim /usr/local/software/apache/conf/httpd.conf 找到下面两行,去掉注…...
电脑/设备网络共享给其他设备上网
文章目录 一、概述二、设置网络共享2.1 电脑可以上网,通过网络共享让其他设备也可以上网2.2 手机如何使用USB数据线共享网络给电脑 一、概述 现在有如下几种情况: 设备本身不能上网,需要通过电脑上网 笔记本WIFI连热点上网,然后…...

vue之虚拟滚动
一、解决的问题 对于大量数据的懒加载,我们可以使用虚拟滚动的技术。虚拟滚动的原理是只渲染可视区域内的数据,当用户滚动时,动态计算并渲染新的可视数据,从而实现大数据量的流畅滚动。 在Vue中,我们可以使用第三方库…...
-Redis的有序集合数据类型介绍)
Redis学习指南(11)-Redis的有序集合数据类型介绍
文章目录 特点和用途常用命令插入操作查询操作删除操作 示例总结 Redis的有序集合数据类型是一种高效的数据结构,能够存储多个成员和对应的分值,并能够根据分值进行快速的查找、插入和删除操作。本文将详细介绍Redis的有序集合数据类型,包括其…...
Spring的纯注解配置
1.环境搭建 1.1.创建工程 1.2.待改造的问题 我们发现,之所以我们现在离不开xml配置文件,是因为我们有一处很关键的配置,如果他要也能用注解配置,那么我们就可以脱离xml文件了: 1.2.1.jdbc配置 <context:propert…...

numpy 筛选多段数据
目录 掩码方式 利用切片 掩码方式 range_to_remove list(range(77-1, 111-1)) list(range(122-1, 135-1))keep_mask np.ones(image0_cut.shape[0], dtypebool)keep_mask[range_to_remove] Falseprocessed_data image0_cut[keep_mask] 利用切片 import numpy as np# 假设…...

【Kotlin】协程的字节码原理
前言 协程是Koltin语言最重要的特性之一,也是最难理解的特性。网上关于kotlin协程的描述也是五花八门,有人说它是轻量级线程,有人说它是无阻塞式挂起,有人说它是一个异步框架等等,众说纷芸。甚至还有人出了书籍专门介…...

区间预测 | Matlab实现LSSVM-ABKDE的最小二乘支持向量机结合自适应带宽核密度估计多变量回归区间预测
区间预测 | Matlab实现LSSVM-ABKDE的最小二乘支持向量机结合自适应带宽核密度估计多变量回归区间预测 目录 区间预测 | Matlab实现LSSVM-ABKDE的最小二乘支持向量机结合自适应带宽核密度估计多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现…...

基于深度学习的实例分割的Web应用
基于深度学习的实例分割的Web应用 1. 项目简介1.1 模型部署1.2 Web应用 2. Web前端开发3. Web后端开发4. 总结 1. 项目简介 这是一个基于深度学习的实例分割Web应用的项目介绍。该项目使用PaddlePaddle框架,并以PaddleSeg训练的图像分割模型为例。 1.1 模型部署 …...
20240115如何在线识别俄语字幕?
20240115如何在线识别俄语字幕? 2024/1/15 21:25 百度搜索:俄罗斯语 音频 在线识别 字幕 Bilibili:俄语AI字幕识别 音视频转文字 字幕小工具V1.2 BING:音视频转文字 字幕小工具V1.2 https://www.bilibili.com/video/BV1d34y1F7…...
Flink 处理函数(1)—— 基本处理函数
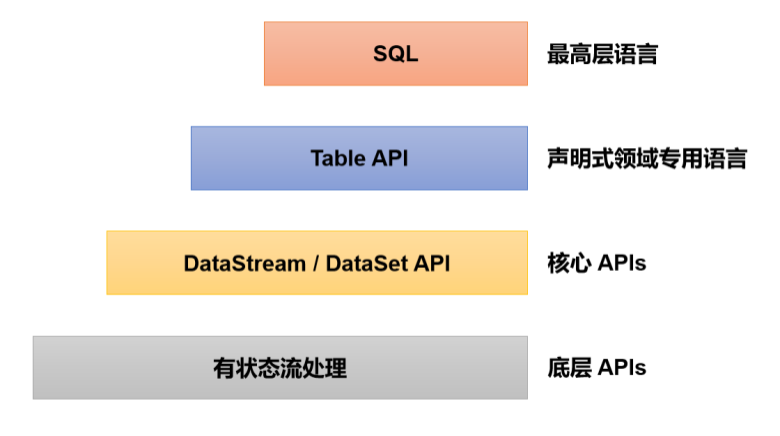
在 Flink 的多层 API中,处理函数是最底层的API,是所有转换算子的一个概括性的表达,可以自定义处理逻辑 在处理函数中,我们直面的就是数据流中最基本的元素:数据事件(event)、状态(st…...
Linux系统下编译MPlayer
一、编译MPlayer 在 http://www.mplayerhq.hu/design7/dload.html 下载MPlayer源码 执行命令: tar -xf MPlayer-1.5.tar.xz cd MPlayer-1.5 ./configure --prefix$(pwd)/install --yasm make make install 然后在install/bin目录下即会生成mplayer的可执行文件 二…...

事务的ACID属性是什么?为什么它们很重要?
引言 在现代的数据库和事务处理系统中,事务处理是一项非常重要的技术。在数据库中,事务是指一组被视为单个逻辑操作单元的SQL语句序列,它们要么全部成功执行,要么全部不执行。事务可以确保数据库在执行时保持一致性和可靠性。ACI…...
计算机毕业设计 基于Java的手机销售网站的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
Redis相关命令详解及其原理
Redis概念 Redis,英文全称是remote dictionary service,也就是远程字典服务。这是kv存储数据库。Redis,包括所有的数据库,都是请求-回应模式,通俗来说就是数据库不会主动地要给前台推送数据,只有前台发送了…...

go语言中的GoMock
GoMock是一个Go框架。它与内置的测试包整合得很好,并在单元测试时提供了灵活性。正如我们所知,对具有外部资源(数据库、网络和文件)或依赖关系的代码进行单元测试总是很麻烦。 安装 为了使用GoMock,我们需要安装gomo…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
