python入门，数据容器的通用操作（len，max，min，sorted）
1.len统计容器内元素个数
2.max统计元素最大元素
3.min统计元素最小元素
4.容器的转化功能
list（容器）将给定容器转化为列表
字符串转列表将字符串内的每一个元素都取了出来作为列表的每一个元素
字典则只会取出它的key，value会消失
str（容器）将给定容器转化为字符串
转化为字符串相当于在容器的两边加上双引号
tuple（容器）将给定容器转化为元组
set（容器）将给定容器转化为集合
转化为集合后会变为无序
5.sorted容器的排序功能
sorted（容器，[reverse = True]）
reverse默认为false，如果想要将排序结果反转，传递一个true
对字典排序会丢失掉它的value
相关文章：
python入门，数据容器的通用操作（len，max，min，sorted）
1.len统计容器内元素个数 2.max统计元素最大元素 3.min统计元素最小元素 4.容器的转化功能 list（容器）将给定容器转化为列表 字符串转列表将字符串内的每一个元素都取了出来作为列表的每一个元素 字典则只会取出它的key，value会消失 str&…...
运筹说 第67期 | 动态规划模型的建立与求解
通过前一期的学习，我们已经学会了动态规划的基本概念和基本原理。本期小编带大家学习动态规划模型的建立与求解。 动态规划模型的建立 一 概述 建立动态规划的模型，就是分析问题并建立问题的动态规划基本方程。 成功地应用动态规划方法的关键&#x…...
大模型压缩与优化的技术原理与创新方法
目录 前言1 模型压缩简介2 知识蒸馏3 模型剪枝3.1 结构化剪枝3.2 非结构化剪枝 4 模型量化4.1 浮点表示 vs 定点表示4.2 位数选择与性能影响4.3 量化技术 5 其他模型压缩方法5.1 Weight Sharing: 参数共享5.2 Low-rank Approximation: 低秩分解5.3 Architecture Search: 神经网…...
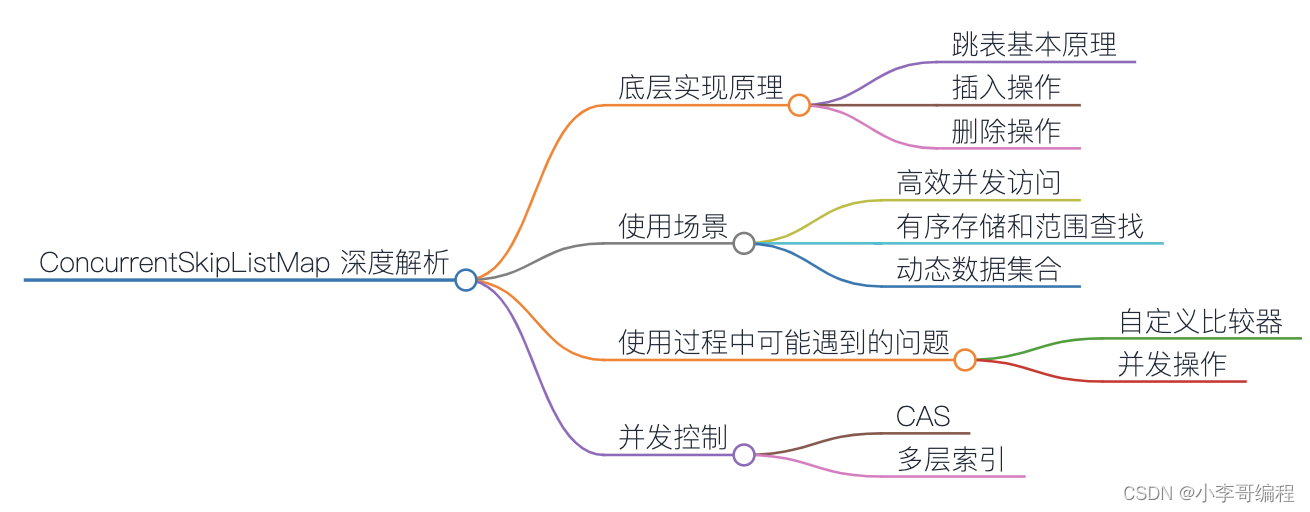
ConcurrentSkipListMap 深度解析
ConcurrentSkipListMap是Java集合框架中的一员，它实现了ConcurrentNavigableMap接口，基于跳表（Skip List）实现，并提供了高效的并发控制。在本文中，我们将深入研究ConcurrentSkipListMap的底层实现原理、适用…...
Vue学习笔记6--配置代理
一、axios Axios 是一个基于 promise 网络请求库，作用于node.js 和浏览器中。 它是 isomorphic 的(即同一套代码可以运行在浏览器和node.js中)。在服务端它使用原生 node.js http 模块, 而在客户端 (浏览端) 则使用 XMLHttpRequests。 二、配置代理 1. 方法一 在…...
嵌入式培训机构四个月实训课程笔记（完整版）-C++和QT编程第三天-C++类和对象高级应用（物联技术666）
链接：https://pan.baidu.com/s/1YRXI0WiABUlYaQXQDNfbyA?pwd=1688 提取码：1688 上午：类和对象高级应用（续） 下午：派生和继承 教学内容： 1、友元 类的私有成员只能在类定义的范围内使用，也就是说私有成员只能通过它的成员函数来访问但是，有时候需要在类的外部访问…...
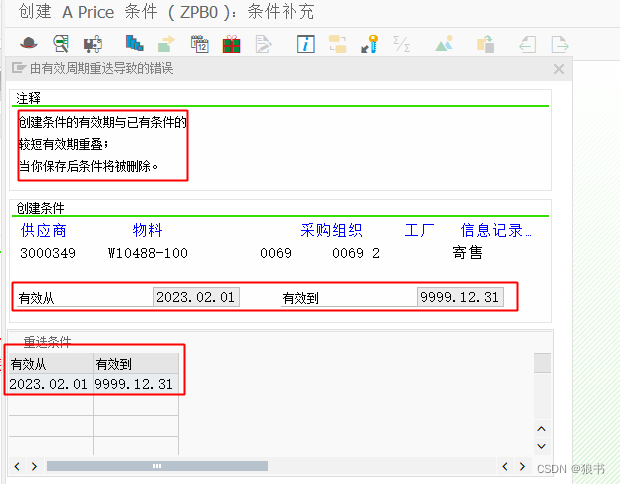
SAP中采购文档价格条件可以删除吗？
首先要声名，基于采购价格条件的严谨性和历史追朔需求，删除属于危险操作。不建议普通用户去执行操作。如果有兴趣，在测试系统中自行测试一下即可。正式系统中，还请慎重处理。 笔者公司日常不会去删除采购价格，日常处理…...
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK设置硬件触发模式（C++）
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK设置硬件触发模式（C） Baumer工业相机Baumer工业相机NEOAPI SDK和硬件触发模式的技术背景Baumer工业相机通过BGAPISDK设置硬件触发模式功能1.引用合适的类文件2.通过BGAPISDK在Line0上施加12V/24V电压信号实…...
嵌入式培训机构四个月实训课程笔记（完整版）-Linux网络编程第二天-tcp编程练习（物联技术666）
点赞+关注，功德无量。更多配套资料，欢迎私信。 网盘链接：百度网盘 请输入提取码 WebServer编程： -------------------------------------- #include <stdio.h> #include <stdlib.h> #include <string.h> #i…...
【IC前端虚拟项目】MVU子模块DS文档编写与注意事项
【IC前端虚拟项目】数据搬运指令处理模块前端实现虚拟项目说明-CSDN博客 DS文档顾名思义就是Design Specification，设计规格文档，对应的就是我们实际一个模块的设计思路和细节： DS - Design Specification（设计规格）："DS" 表示设计规格，它是在架构规格之后，…...
Postgresql 12.2 + PostGIS 3.0.1 安装部署
参考文档： 按照该文档安装即可，如果遇到报错，可以参考下文： https://blog.csdn.net/weixin_41166785/article/details/127674169 所需的安装包 在资源里面（我看下怎么可以不用积分下载） 1、no acceptable…...
MAC iterm 显示git分支名
要在Mac上的iTerm中显示Git分支名，您需要使用一个名为“Oh My Zsh”的插件。Oh My Zsh是一个流行的Zsh框架，它提供了许多有用的功能和插件，包括在终端中显示Git分支名。 以下是在iTerm中显示Git分支名的步骤： 1、安装Oh My Zsh&…...
智慧公厕：利用物联网、云计算和人工智能实现智能化管理与控制
智慧公厕是指利用传感感知、物联网、互联网、大数据、云计算、自动化控制等先进技术，实现对公厕的智能化管理与控制。通过以上高精尖的信息技术手段，可以实时监测厕所内人体活动状态、人体存在状态、空气质量情况、环境变化情况、设施设备运行状态等信息…...
【漏洞复现】Apache Tomcat AJP文件包含漏洞(CVE-2020-1938)
Nx01 产品简介 Apache Tomcat 是一个免费的开源 Web 应用服务器，在中小型企业和个人开发用户中有着广泛的应用。 Nx02 漏洞描述 默认情况下，Apache Tomcat会开启AJP连接器，由于AJP服务（8009端口）存在文件包含缺陷&…...
[渗透测试学习] Hospital - HackTheBox
文章目录 信息搜集getshell提权信息搜集 nmap扫描一下端口 发现8080端口和443端口有http服务 然后发现3389端口是启用了ms-wbt-server服务 在对443端口的扫描没有收获，并且只有邮箱登录界面无法注册 接着看向8080端口，我们随便注册用户登录后发现有文件上传功能 getshell …...
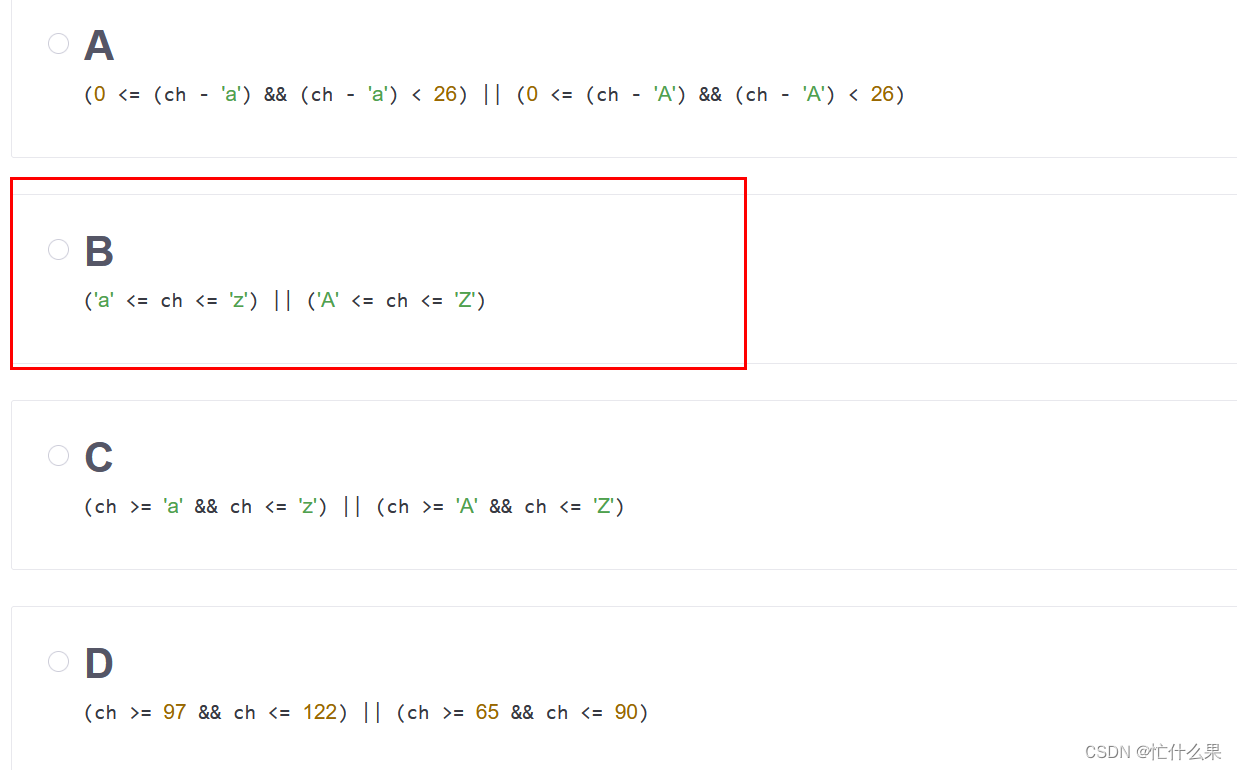
C技能树-学习笔记（1-2）C语言概述和数据类型
参考：https://edu.csdn.net/skill/c 1、输出 “Hello, World!” 字符串，请选出错误答案。 2、错误的print函数。 for … in …：是python的语法，C语言的写法是for (;😉 3、C标准 没有C19标准。 4、了解C编译管道 …...
设计模式入门
0. 类图 1. 设计原则 1.单一职责原则：每个类只有一个功能 2.开放封闭原则：模块和函数应该对扩展开放(对提供方)，对修改关闭(对使用方) 3.里氏代换原则：子类拥有父类的所有方法和属性，从而可以减少创建类的工作量 4.依…...
EasyExcel下载EXCEL文件，后台通过流形式输出到前端浏览器下载方式输出
前端代码（参考）：$("#import").on(click, function(){var createDate$("#createdDate").val();var key1$("#key1").val();if(createDatenull||createDate""){layer.msg("请选择创建时间段&#…...
Pandas实战100例 | 案例 56: 创建多重索引
案例 56: 创建多重索引 知识点讲解 在 Pandas 中，多重索引（或层次化索引）提供了在 DataFrame 中表示多维数据的方式。这使得数据分析在多个级别上更加灵活和强大。 创建多重索引: 通过使用 set_index 方法并传入多个列名，可以在…...
解决“nacos默认secret.key配置不当权限绕过漏洞“
一、前言 nacos 2.2.0.1以下版本会有一个nacos默认secret.key配置不当权限绕过漏洞，等级为高危。形成原因是nacos的配置文件中存在这么一个secret.key默认配置： nacos.core.auth.plugin.nacos.token.secret.keySecretKey01234567890123456789012345678…...
Linux 文件类型，目录与路径，文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件：-（纯文本文件，二进制文件，数据格式文件） 如文本文件、图片、程序文件等。 目录文件：d（directory） 用来存放其他文件或子目录。 设备…...
uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中，每个页面需要使用ref，onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入，需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...
UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法：netstat [选项] 功能：查看网络状态 常用选项： n 拒绝显示别名&#…...
vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现，这取决于你是想在组件内部直接设置，还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法： 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
什么是EULA和DPA
文章目录 EULA（End User License Agreement）DPA（Data Protection Agreement）一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA（End User License Agreement） 定义： EULA即…...
前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包（Closure）？闭包有什么应用场景和潜在问题？2.解释 JavaScript 的作用域链（Scope Chain） 二、原型与继承3.原型链是什么？如何实现继承&a…...
uniapp中使用aixos 报错
问题： 在uniapp中使用aixos，运行后报如下错误： AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中，提示一个依赖外部头文件的cpp源文件需要同步，点…...
Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
云原生安全实战：API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填！ 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关（API Gateway） API网关是微服务架构中的核心组件，负责统一管理所有API的流量入口。它像一座…...