贪心+蓝桥杯
原题路径
题目思路 : 思路很简单,肯定是贪心做法,要使总代价最小,需用那些出现次数比avg多的数来替换那些没有出现或者是出现次数少于avg的数, 所以我们存当前数每次出现的代价是多少 ,枚举每一个 0 - 9 之间的数 ,如果当前数出现的次数多于avg,那么说明需要减少,每次用最小的代价替换即可
由于我们并不知道替换的数是哪一个,但由于题目中说明了每个数都会出现 n / 10 次,所以证明一旦多出来的数必定会替换为另一个数,故我们只需要从小到大替换,将 avg 个当前数中价值最大的保存即可。#include <iostream> #include <cstring> #include <algorithm>using namespace std;const int N = 1e5 + 10;int n; int a[N] , b[N]; vector<int> h[N];int main() {cin >> n;for(int i = 1 ; i <= n ; i ++){int a , b;cin >> a >> b;h[a].push_back(b);}int avg = n / 10;long long res = 0;for(int i = 0 ; i < 10 ; i ++){int x = h[i].size();if(x > avg){sort(h[i].begin() , h[i].end());for(int j = 0 ; j < h[i].size() - avg ; j ++){res += h[i][j];}}}printf("%lld" , res);return 0; }
相关文章:

贪心+蓝桥杯
原题路径 题目思路 : 思路很简单,肯定是贪心做法,要使总代价最小,需用那些出现次数比avg多的数来替换那些没有出现或者是出现次数少于avg的数, 所以我们存当前数每次出现的代价是多少 ,枚举每一个 0 - 9 之间的数 ,如果当前数出现…...

第二篇:新建node项目并运行
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 安装 Node.js:首先,确保你的…...

阳光保险选择OceanBase稳定运行超700天
阳光保险集团成立于 2005 年 7 月,旗下拥有财产保险、人寿保险、信用保证保险、资产管理等多家专业子公司,是全球市场化企业中成长最快的集团公司之一,目前位列中国保险行业前八。随着数字化升级趋势的不断加速,很多企业产生将软硬…...

最强大脑闪电心算草稿1
#include<bits/stdc.h> #include<windows.h> using namespace std; int main() {double speed,n,op,sum0;int ans;srand(time(NULL));cout<<"请输入加(1)/减(2)/加减混合(3):";cin>>op;cout<<"请输入题目数量:";cin>>…...

融优学堂-艺术史
导论4 1.【单选题】根据导论的讲解,下列表述正确的是()。(1)艺术品是因人的活动而被创造出来的人工制品。(2)许多物品被制造出来时,最初的目的是满足某种实用的用途,而不…...
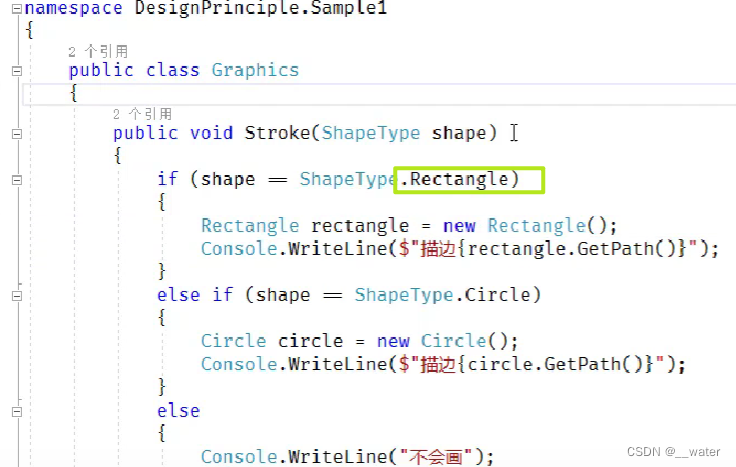
༺༽༾ཊ—设计-七个-07-原则-模式—ཏ༿༼༻
第七原则:迪米特职责 类与类之间的耦合度尽可能低 换言之,我们可以理解成———只与直接朋友说话,不跟陌生人说话 直接朋友: 通过方法传参传进来的朋友, 类自己的字段, 构造函数进来的也是直接朋友&…...

一篇文章带你搞懂---全排序
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 全排序(Permutation)是指将一组元素按照一定的顺序进行排列的过程。在计算机科学中,全排序是一…...

提升问题检索的能力
事实上,在信息极度丰富的时代,信息检索和筛选能力格外重要。一些搜索引擎的出现已极大地方便了我们日常的信息检索,此处需要注意的是我们不能仅仅局限于常见的搜索引擎,也需要关注和积累一些专业平台或是具有集成功能的引擎&#…...

软件测试|SQLAlchemy query() 方法查询数据
简介 上一篇文章我们介绍了SQLAlchemy 的安装和基础使用,本文我们来详细介绍一下如何使用SQLAlchemy的query()方法来高效的查询我们的数据。 创建模型 我们可以先创建一个可供我们查询的模型,也可以复用上一篇文章中我们创建的模型,代码如…...
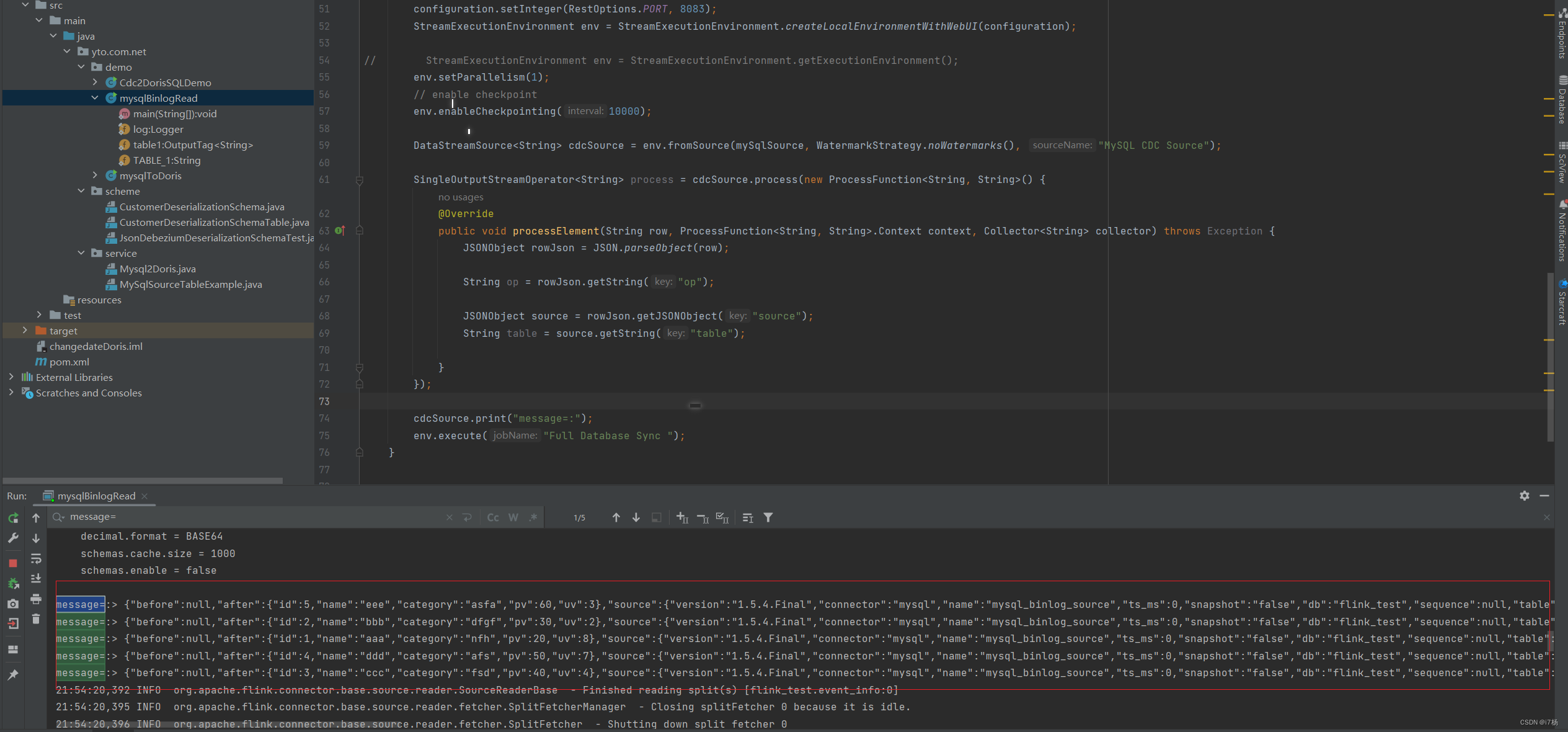
FlinkCDC的分析和应用代码
前言:原本想讲如何基于Flink实现定制化计算引擎的开发,并以FlinkCDC为例介绍;发现这两个在表达上不知以谁为主,所以先分析FlinkCDC的应用场景和技术实现原理,下一篇再去分析Flink能在哪些方面,做定制化计算…...
序章 搭建环境篇—准备战士的剑和盾
第一步:安装node.js Node.js 内置了npm,只要安装了node.js,就可以直接使用 npm,官网地址: Download | Node.js 在这里不建议安装最新版本的node.js,可以选跟我一样的版本,node版本v16.13.2 链…...

【C++】vector的使用及模拟实现
目录 一、vector的介绍及使用1.1 介绍vector1.2 vector的使用1.2.1 构造1.2.2 遍历访问1.2.3 容量空间1.2.4 增删查改 二、vector的模拟实现2.1 成员变量2.2 迭代器相关函数2.3 构造-析构-赋值重载2.3.1 无参构造2.3.2 有参构造12.3.3 有参构造22.3.4 拷贝构造2.3.5 赋值重载2.…...

【数据库】sql优化有哪些?从query层面和数据库层面分析
目录 归纳sql本身的优化数据库层面的优化 归纳 这类型问题可以称为:Query Optimization,从清华AI4DB的paper list中,该类问题大致可以分为: Query RewriterCardinality EstimationCost EstimationPlan Optimization 从中文的角…...

nginx基本优化
安装nginx隐藏版本号 查看百度web服务器 [rootcjq11 ~]# curl -I http://www.baidu.com 隐藏nginx服务器版本号 [rootcjq11 ~]# cd /usr/local/src/nginx-1.22.0/ [rootcjq11 nginx-1.22.0]# vim src/core/nginx.h第13、14行修改版本号和服务器名称 [rootcjq11 nginx-1.2…...

软件测试|使用selenium处理单选框和多选框
简介 我们在web自动化测试工作中,经常会遇到对单选框(Radio Buttons)或者多选框(Checkboxes)进行操作的场景,单选框和多选框主要是用于我们做出选择或提交数据。本文将主要介绍selenium对于单选框和多选框…...
的有效值列表)
openssl3.2 - EVP_CIPHER_fetch算法名称字符串(参数2)的有效值列表
文章目录 openssl3.2 - EVP_CIPHER_fetch算法名称字符串(参数2)的有效值列表概述如何找到算法名称字符串列表?openssl-3.2.0\providers\implementations\include\prov\names.h备注END openssl3.2 - EVP_CIPHER_fetch算法名称字符串(参数2)的有效值列表 概述 进行加解密时, 先…...

vue3中的hook公共函数封装及运用
vue3 中的 hooks 就是函数的一种写法,就是将文件的一些单独功能的js代码进行抽离出来,放到单独的js文件中,或者说是一些可以复用的公共方法/功能 使用Vue3的组合API封装的可复用的功能函数自定义hook的作用类似于vue2中的mixin技术自定义Hook…...

广州市工信局、天河区商务金融局及广州专精特新促进会走访思迈特
2024年1月11日下午,广州市工信局、天河区商务金融局及广州专精特新促进会相关负责人莅临广州思迈特软件总部调研指导,思迈特软件总裁兼COO姚诗成代表公司热情接待,并陪同调研。 调研组实地参观了思迈特软件,深入了解了思迈特发展历…...

vi编辑器显示行号和不显示行号切换命令
文章目录 1.临时生效只需要在vi编辑器里面输入1.1.显示行号1.2.不显示行号 2.永久生效 1.临时生效只需要在vi编辑器里面输入 1.1.显示行号 set number 或者 set nu如下图 1.2.不显示行号 set nonumber 或者 set nonu2.永久生效 首先打开配置文件/etc/vim/vimrc,向文件中添…...

使用 LLVM clang C/C++ 编译器编译 boost 基础框架类库
1、下载 boost 1.84 库的源代码放到待编译目录 2、解压并接入 boost 1.84 库源码的根目录 搜索默认的 clang 版本,WSL 2.0/Ubuntu 18.04 LTS 为 clang 6.x 执行命令: ./bootstrap.sh --with-toolsetclang ./b2 toolsetclang 另外一个方法比较麻烦需要…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
