前端浮点和16进制互转
一、浮点转16进制数据
//浮点数转16进制
function singleToHex(t) {if (t == "") {return "";}t = parseFloat(t.substr(0, 4));if (isNaN(t) == true) {return "Error";}if (t == 0) {return "00000000";}var s,e,m;if (t > 0) {s = 0;}else {s = 1;t = 0 - t;}m = t.toString(2);if (m >= 1) {if (m.indexOf(".") == -1) {m = m + ".0";}e = m.indexOf(".") - 1;}else {e = 1 - m.indexOf("1");}if (e >= 0) {m = m.replace(".", "");}else {m = m.substring(m.indexOf("1"));}if (m.length > 24) {m = m.substr(0, 24);}else {m = FillString(m, "0", 24, false)}m = m.substring(1);e = (e + 127).toString(2);e = FillString(e, "0", 8, true);var r = parseInt(s + e + m, 2).toString(16);r = FillString(r, "0", 8, true);var value = InsertString(r, " ", 2).toUpperCase();return value.substr(6, 2) + value.substr(9, 2) + value.substr(0, 2) + value.substr(3, 2)
}
二、16进制转浮点(单精度)
//16进制转浮点数(单精度)
function HexToDouble(hex) {let S, E, M, result;S = hex >>> 31;E = ((hex << 1) >>> 24);M = (hex << 9) >>> 9;if (E === 0xff) {if (M === 0x0) {return ((-1) ** S) * Infinity;} else {return NaN;}}result = ((-1) ** S) * (M / (1 << 23) + !!(E)) * (2 ** (E - 127 + !E));return result;
}
三、16进制转浮点(双精度)
//16进制转浮点数(双精度)
function hexToSingle(t, fixed = 2) {t = t.replace(/\s+/g, "");if (t == "") {return "";}if (t == "00000000") {return "0";}if ((t.length > 8) || (isNaN(parseInt(t, 16)))) {return "Error";}if (t.length < 8) {t = FillString(t, "0", 8, true);}t = parseInt(t, 16).toString(2);t = FillString(t, "0", 32, true);var s = t.substring(0, 1);var e = t.substring(1, 9);var m = t.substring(9);e = parseInt(e, 2) - 127;m = "1" + m;if (e >= 0) {m = m.substr(0, e + 1) + "." + m.substring(e + 1)}else {m = "0." + FillString(m, "0", m.length - e - 1, true)}if (m.indexOf(".") == -1) {m = m + ".0";}var a = m.split(".");var mi = parseInt(a[0], 2);var mf = 0;for (var i = 0; i < a[1].length; i++) {mf += parseFloat(a[1].charAt(i)) * Math.pow(2, -(i + 1));}m = parseInt(mi) + parseFloat(mf);if (s == 1) {m = 0 - m;}if (fixed) {m = m.toFixed(fixed).replace(/[.]?0+$/, "")}return m;
}
相关文章:

前端浮点和16进制互转
一、浮点转16进制数据 //浮点数转16进制 function singleToHex(t) {if (t "") {return "";}t parseFloat(t.substr(0, 4));if (isNaN(t) true) {return "Error";}if (t 0) {return "00000000";}var s,e,m;if (t > 0) {s 0;}e…...
与equals()的相关规定)
Java中hashCode()与equals()的相关规定
API文件有对对象的状态制定出必须遵循的规则。hashCode()和equals()是object中定义的两个方法,它们都与对象的相等性有关。 通常情况下我们需要同时使用这两个方法来判断两个对象是否相等,只有两个对象的equals()方法返回true,并且它们的has…...

转行做鸿蒙开发首先需要学习哪些?
随着越来越多的企业和团队开始布局鸿蒙生态,鸿蒙开发人才的需求也呈现出井喷式的增长。对于开发者而言,掌握鸿蒙开发技能不仅意味着能够抓住这个千载难逢的机遇,更意味着能够在未来的科技竞争中占据先机。 在这个变革的时代,鸿蒙开…...
8x8离散余弦的快速精确实现使用数据流单指令多数据扩展指令集进行转换MMX 说明书
1.https://www.cs.cmu.edu/~barbic/cs-740/ap922.pdf 2.FFmpeg: libavcodec/x86/fdct.c Source File 再学FDCT快速精确实现协议改写浮点FDCT, ffmpeg的dct使用的就是这个快速精确协议。 3.http://dspace.fcu.edu.tw/bitstream/2377/30265/1/ICM%204-1.pdf 我想如把所有余弦…...
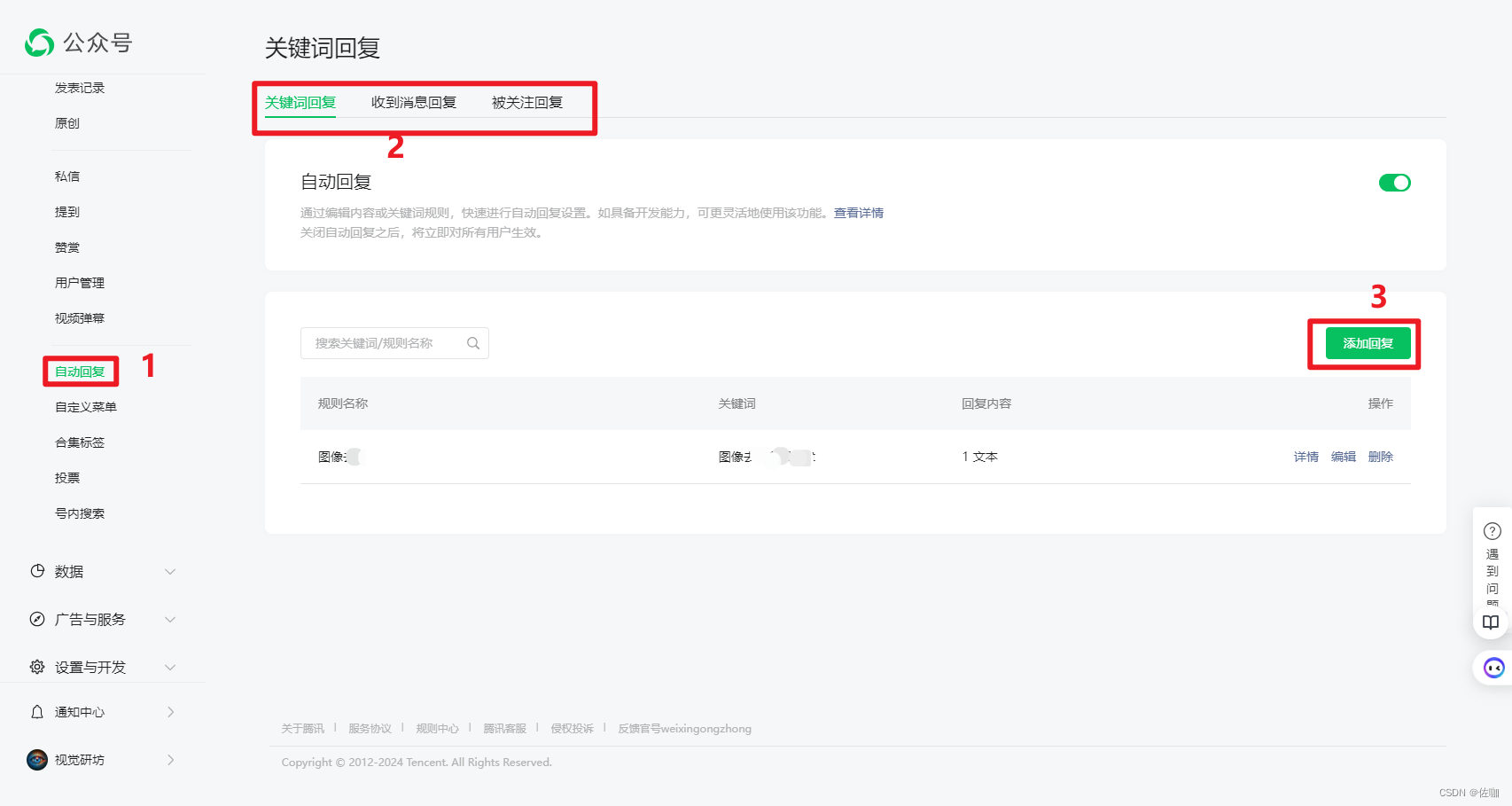
微信公众号注册(详细图文教程)
目录 一、公众号注册准备1.1 准备事项1.2 个人注册1.3 企业注册 二、公众号注册2.1 基本信息填写2.2 选择类型2.3 信息登记2.4 公众号信息2.5 修改头像2.6 自动回复消息 三、总结 一、公众号注册准备 1.1 准备事项 公众号名称:公众号名称可以由中文、英文、数字、…...
)
排序算法-冒泡排序(含C语言代码示例)
一、算法介绍 冒泡排序是一种简单的排序算法,其核心思想是重复地遍历待排序列表,比较并交换相邻元素,使得较大的元素逐渐“冒泡”到列表的末尾,而较小的元素则逐渐上浮至列表的前端。该算法的名字源于类比元素的移动过程ÿ…...

易基因:表观遗传学和表观转录组修饰在植物金属和准金属暴露中的作用 | 抗逆综述
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。 非必需金属(non-essential metal)和准金属(metalloid,也称类金属)对土壤的污染是全球许多地区面临的严重问题。这些非必需金属…...

使用Guava Retrying优雅的实现业务异常重试
上次写过一篇如何使用spring retry来实现业务重试的文章:https://blog.csdn.net/Kingsea442/article/details/135341747 尽管 Spring Retry 工具能够优雅地实现重试,但它仍然存在两个不太友好的设计: 重试实体被限定为 Throwable 子类&#…...
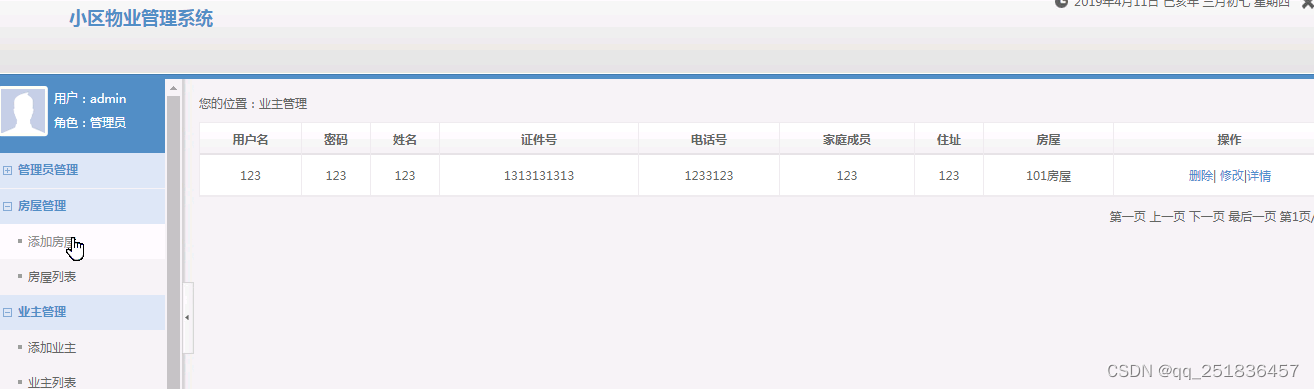
java SSM物业管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM物业管理系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和 数据库,系统主要采用B/…...

Hive使用shell调用命令行特殊字符处理
1.场景分析 数据处理常用hive -e的方式,通过脚本操作数仓,过程中常常遇到特殊字符的处理,如单双引号、反斜杠、换行符等,现将特殊字符用法总结使用如下,可直接引用,避免自行测试的繁琐。 2.特殊字符处理 …...

服务器里面很卡,打开文件卡住了一般是什么问题,怎么解决
随着互联网业务的快速发展,各项业务都绕不开服务器。在日常使用中,服务器有着非常重要的作用。而我们日常使用中,也会遇到各种各样的问题。最近就有遇到用户联系咨询德迅云安全,询问自己服务器突然很卡,打开文件都卡住…...

linux 测试网络传输速度
在linux和macos中看不到文件复制速度,往往不清楚smb或者afp的传输速度。 dd命令可以测试磁盘io速度,当然也可以测试网络传输速度。 首先要挂载afp或者smb,此步略过。 然后准备好一定体积的测试文件(最好大点,比如1G以上),使用以下命令测试传输速度: dd if=/smb/TestI…...

GO——锁
公平锁和非公平锁 参考:https://blog.csdn.net/weixin_39309402/article/details/106466843 公平锁: 多个线程排队去获取锁优点 所有线程都能获取到资源 缺点 除第一个线程,其他队列中的线程(阻塞中)都需要唤醒&…...
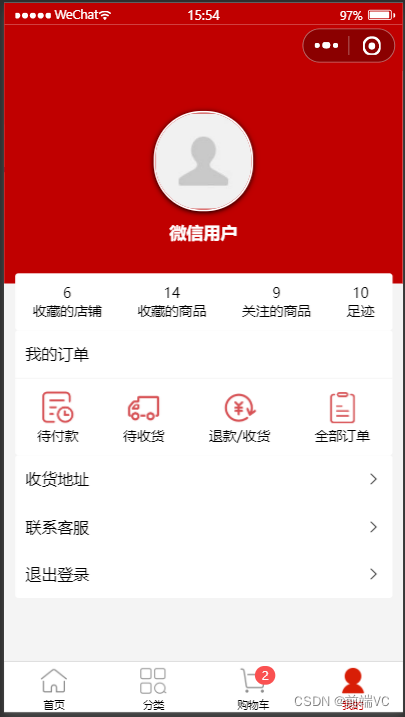
分析一个项目(微信小程序篇)三
目录 接下来分析接口方面: home接口: categories接口: details接口: login接口: 分析一个项目讲究的是如何进行对项目的解析分解,进一步了解项目的整体结构,熟悉项目的结构,能够…...

element+vue 之图片放大器
1.安装插件 npm install vue-photo-zoom-pro2.main.js导入 // 放大镜 import VuePhotoZoomPro from vue-photo-zoom-pro Vue.use(VuePhotoZoomPro)3.页面使用 <vue-photo-zoom-pro:url"imgUrl":out-zoomer"true":scale"2"style"width:…...
Vue学习笔记3--全局事件总线
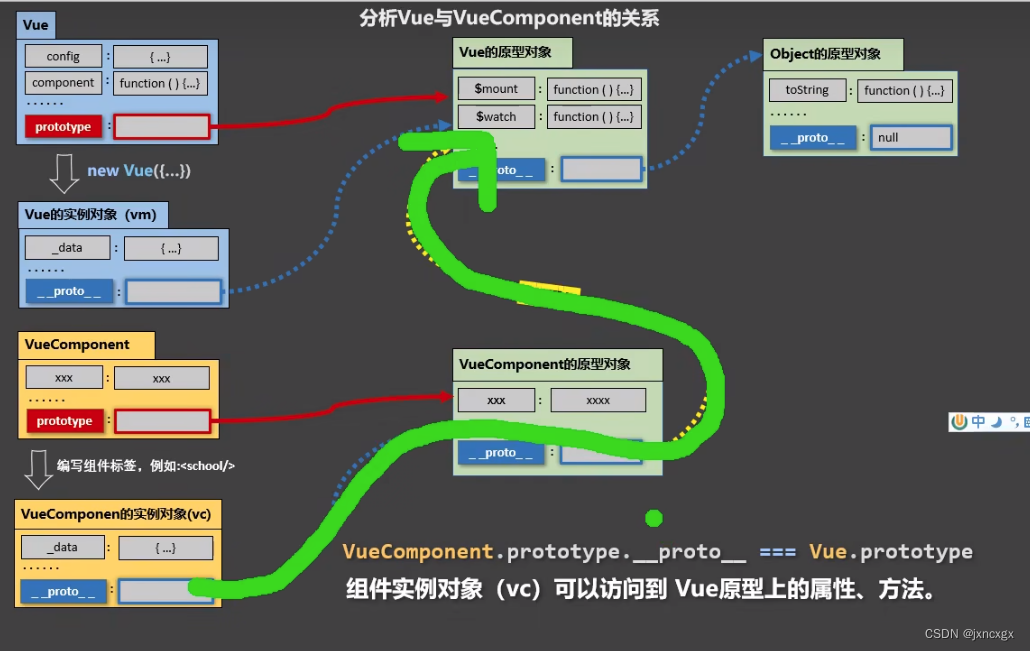
Vue学习笔记3—全局事件总线 1.全局事件总线可以实现任意组件间通信 X需具备的条件: 所有的组件都要能看见X可以调用$on $off $emitVue.prototype.x {a:1, b:2} 可以被所有组件看见VueComponent.protoype.proto Vue.prototype组件实例对象(vc)可以访问到Vue原型上…...

科学和统计分析软件GraphPad Prism mac介绍说明
GraphPad Prism for Mac是一款科学和统计分析软件,旨在帮助研究者、科学家和学生更轻松地处理和可视化数据。 GraphPad Prism for Mac是一款功能强大、易于使用的科学和统计分析软件,适用于各种类型的数据处理和可视化需求。无论您是进行基础研究、临床试…...
[学习笔记]刘知远团队大模型技术与交叉应用L1-NLPBig Model Basics
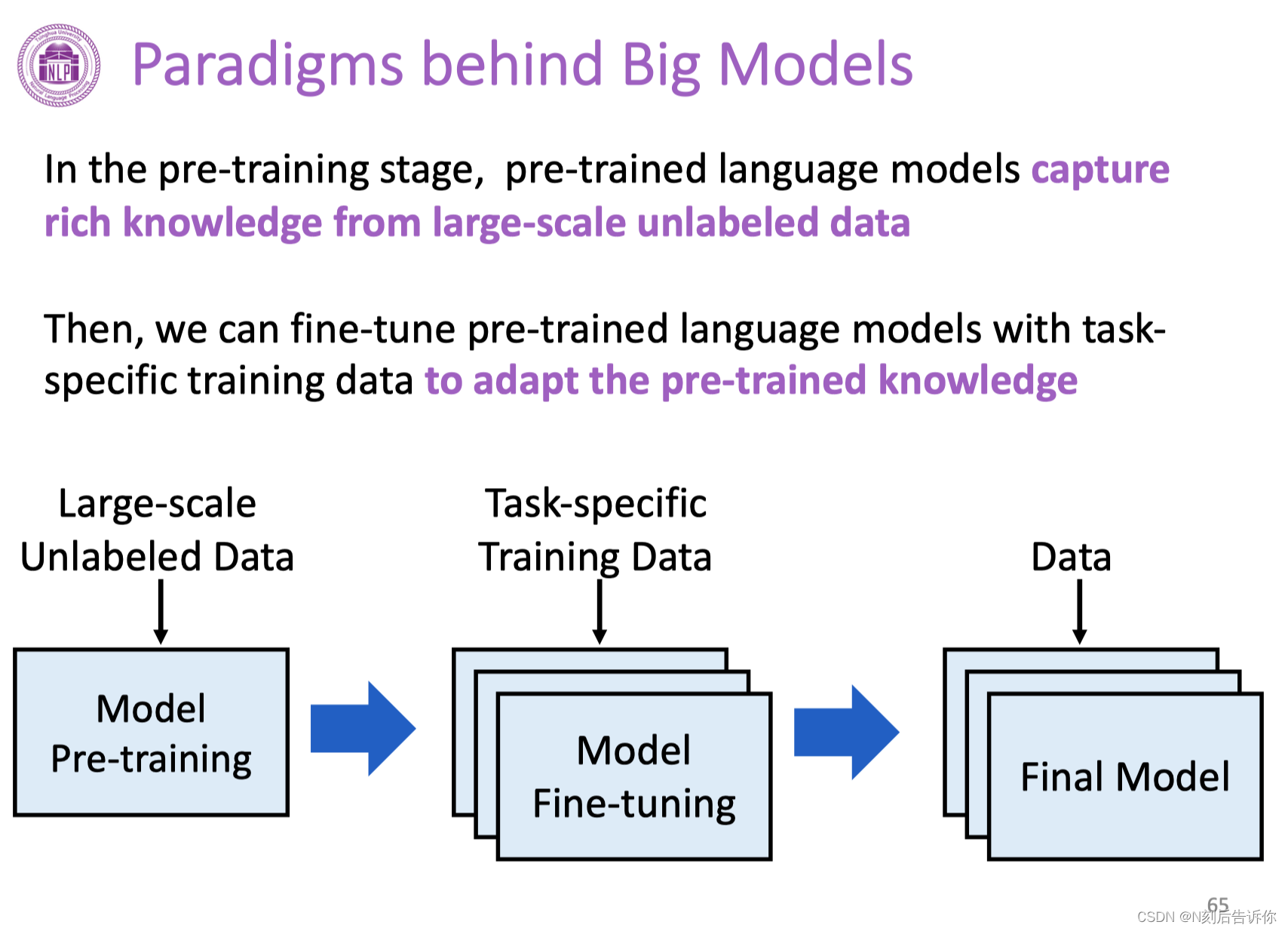
本节主要介绍NLP和大模型的基础知识。提及了词表示如何从one-hot发展到Word Embedding。语言模型如何从N-gram发展成预训练语言模型PLMs。然后介绍了大模型在NLP任务上的表现,以及它遵循的基本范式。最后介绍了本课程需要用到的编程环境和GPU服务器。 一篇NLP方向的…...
概率论与数理统计————古典概型、几何概型和条件概率
一、古典概型 特点 (1)有限性:试验S的样本空间的有限集合 (2) 等可能性:每个样本点发生的概率是相等的 公式:P(A) A为随机事件的样本点数;S是样本…...

C#编程-使用事件
使用事件 事件是一个动作或发生的事情,例如:鼠标点击、按键、鼠标移动或系统产生的通知。应用程序可以在事件发生的时候做出响应。通知的一个示例是中断。事件是对象发生的消息以表示事件的发生。事件是进程内通信的有效方法。它们对对象时有用的,因为它们标识了单个状态改…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
