【网络安全】【密码学】【北京航空航天大学】实验一、数论基础(上)【C语言和Java实现】
实验一、数论基础(上)
一、实验目的
1、通过本次实验,熟悉相关的编程环境,为后续的实验做好铺垫;
2、回顾数论学科中的重要基本算法,并加深对其的理解,为本学期密码学理论及实验课程打下良好的基础。
二、实验原理
数论主要研究的是整数的运算及性质,许多常用的加密算法都用到了数论知识。
三、实验环境
本次实验的实验环境为Dev-C ++ 5.11,以及IntelliJ IDEA IDE。
四、实验内容
1、厄拉多塞筛算法(Sieve of Eratosthenes)
(1)、算法原理
辅助变量 i 从 2 到 N的平方根 遍历,在 [2,N] 区间 当中将所有 i 的倍数删除,剩下的数即为 [2,N] 中的全部素数。
(2)、算法流程
本算法的大致流程如下图所示:
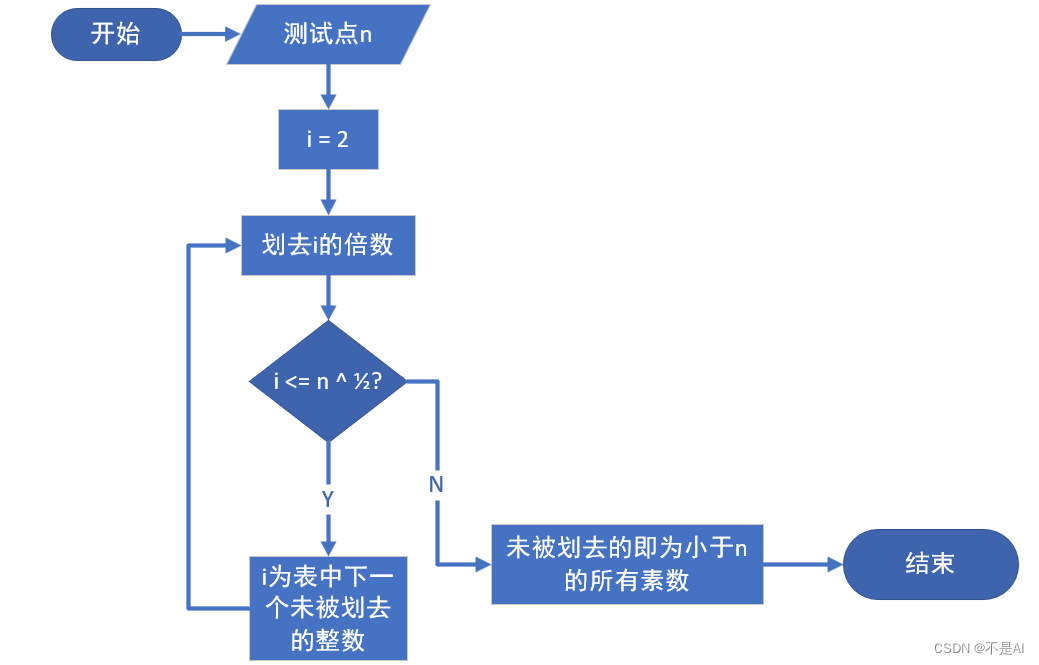
(3)、算法的代码实现(C语言)
#include <stdio.h>
#include <math.h>int flags[10010] = { 0 }; // 0代表质数,1代表合数
int isprime[10010] = { 0 }; // 质数的集合
int i, j;
int num; // [2,N]中质数的个数void getprimes(unsigned long long N);int main()
{unsigned long long N;printf("请输入N: ");scanf("%lld", &N);getprimes(N);return 0;
}void getprimes(unsigned long long N)
{for(i = 2;i < sqrt(N) + 1;i ++){if(flags[i] == 0){j = i * i; //从i的平方开始标记 while(j <= N){//将所有i的倍数(除i本身之外)标记为合数flags[j] = 1; j += i;}}}printf("[2,N]中的全部质数为:\n");for(i = 2;i <= N;i ++){if(flags[i] == 0) //若i为质数{num ++; printf("%d ", i);}}printf("\n");printf("共 %lld 个", num);
}
(4)、算法测试
测试点1:n = 2
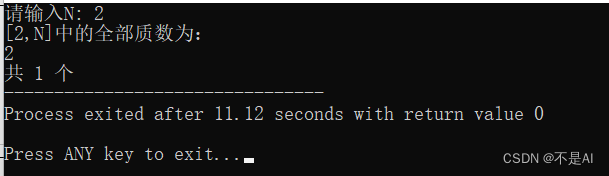
测试点2:n = 103:
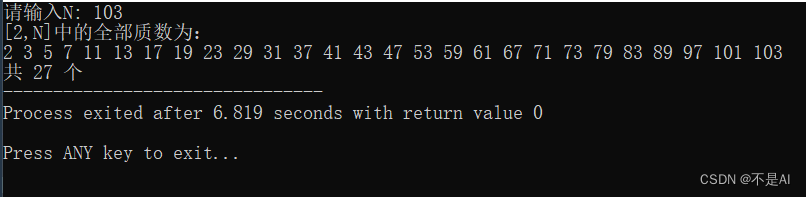
测试点3:n = 10000
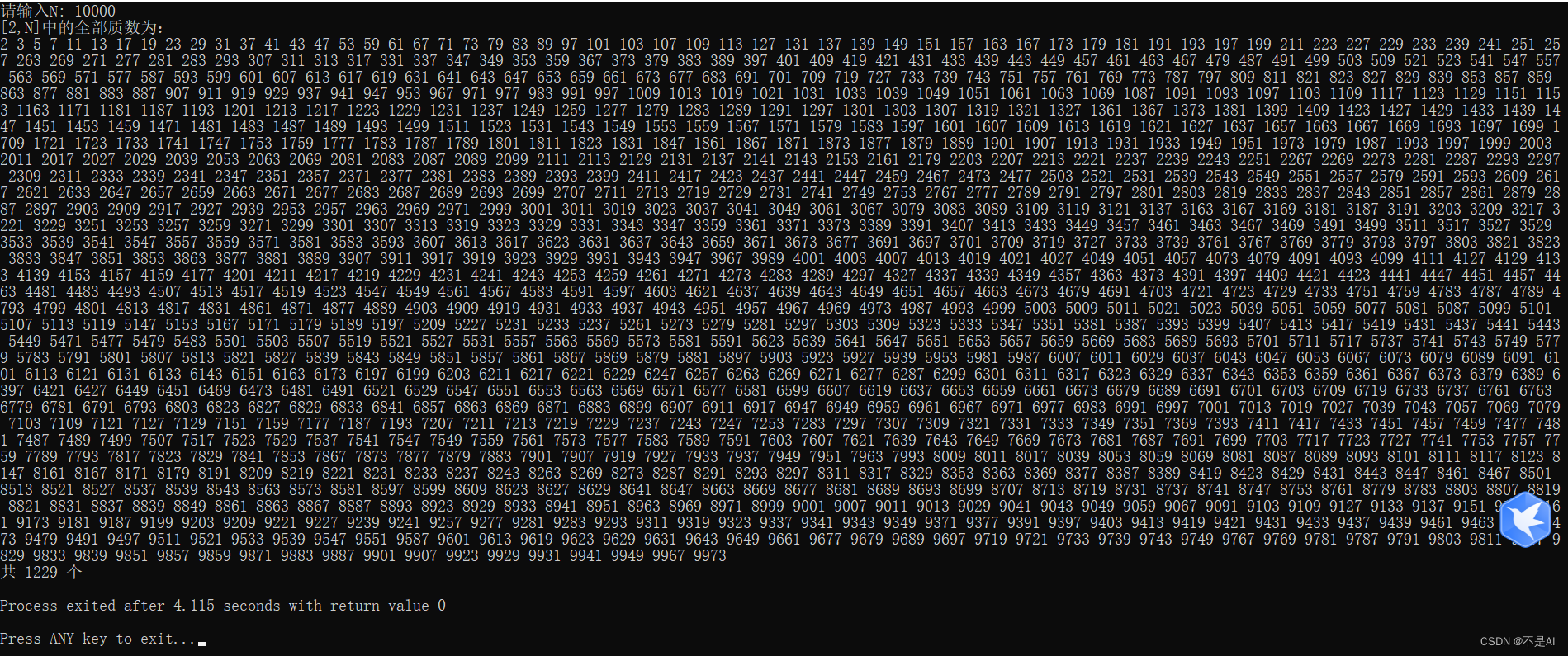
2、简单欧几里得算法(Simple Euclid’s Algorithm)
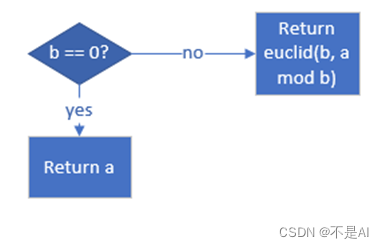
(1)、算法原理
简单欧几里得算法用于求2个整数a和b的最大公约数,该算法原理基于等式gcd(a,b)=gcd(b,a mod b),其中 gcd(a, b) 表示a和b的最大公约数,mod表示取模运算。
(2)、算法流程
本算法的大致流程如下图所示:
(3)、算法的代码实现(C语言)
#include <stdio.h>
#include <math.h>int getgcd(int a, int b);//求a和b的最大公因数int main(){int a, b;printf("请输入整数a: ");scanf("%d", &a);printf("请输入整数b: ");scanf("%d", &b);printf("%d 和 %d 的最大公约数是 %d", a, b, getgcd(a, b));return 0;
}int getgcd(int a, int b){if(b == 0){return abs(a);}else{return getgcd(b, a % b);}
}
(4)、算法测试
测试点1:a = 7, b = 5
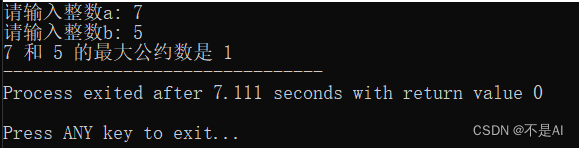
测试点2:a = 31, b = -13
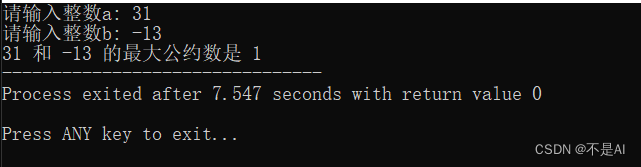
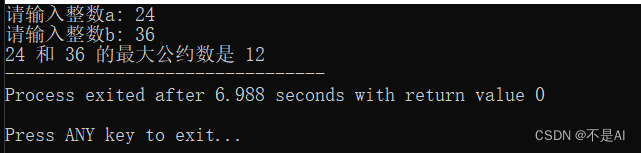
测试点3:a = 24, b = 36;
(5)大整数测试
测试算法在极大整数(位数远超出C语言中 unsigned long long 所能表示的范围)上的表现。使用 Java 语言中的大整数类 BigInteger实现。算法的完整代码如下:
import java.math.BigInteger;public class euclid {public static BigInteger euclidfunc(BigInteger a, BigInteger b){BigInteger zero;BigInteger tmp;zero = new BigInteger("0");while((b.compareTo(zero))!= 0) {tmp = a.mod(b);a = b;b = tmp;}if((b.compareTo(zero)) == 0) {return a;}return zero;}public static void main(String[] args) {BigInteger a, b;a = new BigInteger(""); // 以字符串的形式填入测试点a的数值b = new BigInteger(""); // 以字符串的形式填入测试点a的数值System.out.println("a 和 b 的最大公约数是:");System.out.println(euclidfunc(a, b));}
}
测试方面,选取2组互质的大整数,以及1组最大公约数为2的大偶数,作为测试用例,以验证算法对于大整数的正确性。
大整数测试点1:
a = 2461502723515673086658704256944912426065172925575,
b = 1720876577542770214811199308823476528929542231719
运行结果:
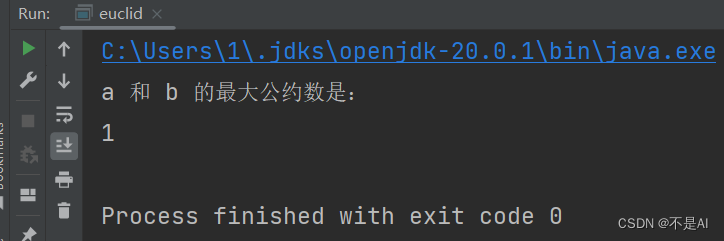 大整数测试点2:
大整数测试点2:
a = 137096164691449488835122291235023051763859318102840889067550902
3843189897270890443917889846802171079840187598665712521108447262149
9595371254346390738382042,
b = 192350399949876251675909634808997772559337752383120440971227732
5564753027680631763602672767980082537045932161772487151544214743242
0951257037823141069640181
运行结果:
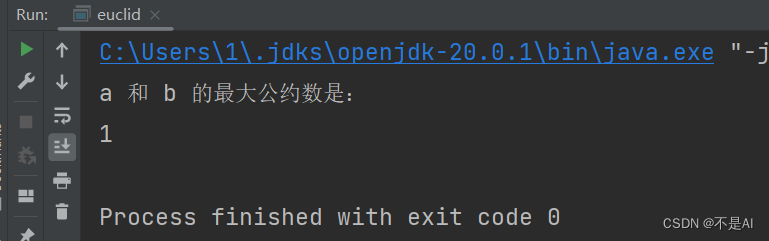 大整数测试点3:
大整数测试点3:
a = 965578072786402991215194630452063779349788872980869942115905155
7171732595578592378315943243630787051274235487747679004689180215305
3719263845602618422474671707896136814707875793300040916757228826108
4994903112959425534780109130436805236126554005262552907029834903821
91419067057726624348815391509161304477322782,
b = 146116799305702219220540123503890666704710410600856387071776221
5924772567527599977981699318091564264712437997953740725104236453636
8053733781377426865890713096999414678345169283722277214494143490905
0652825715582967684984814095461041109999161468223272534833391335036
612863782740784573110824091866969655931097032
运行结果:
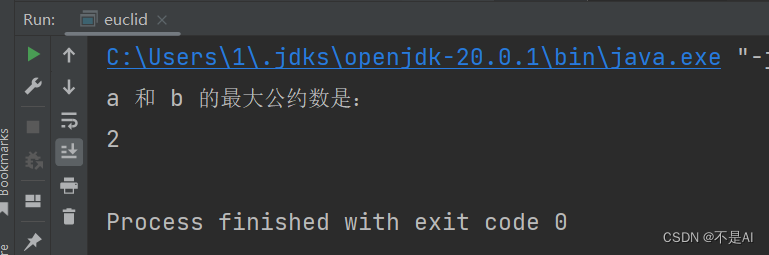
至此,本次实验结束。
五、参考文献
1、《密码编码学与网络安全——原理与实践(第七版)》(Cryptography and Network Security, Principles and Practice, Seventh Edition),【美】威廉 斯托林斯 William Stallings 著,王后珍等 译,北京,电子工业出版社,2017年12月。
2、《密码学实验教程》,郭华 刘建伟等 主编,北京,电子工业出版社,2021年1月。
相关文章:

【网络安全】【密码学】【北京航空航天大学】实验一、数论基础(上)【C语言和Java实现】
实验一、数论基础(上) 一、实验目的 1、通过本次实验,熟悉相关的编程环境,为后续的实验做好铺垫; 2、回顾数论学科中的重要基本算法,并加深对其的理解,为本学期密码学理论及实验课程打下良好…...

Go语言的sync.Pool如何使用?使用场景具体有哪些?
sync.Pool 是 Go 标准库中提供的一个对象池(Object Pool)的实现。对象池是一种用于缓存和复用对象的机制,可以在一定程度上减轻内存分配的开销。sync.Pool 专门用于管理临时对象,适用于一些需要频繁创建和销毁的短暂对象ÿ…...

MySQL单表查询练习题
一、创建表的素材 表名:worker——表中字段均为中文,比如:部门号、工资、职工号、参加工作等 CREATE TABLE worker ( 部门号 int(11) NOT NULL, 职工号 int(11) NOT NULL, 工作时间 date NOT NULL, 工资 float(8,2) NOT NULL, 政治面貌 …...

Spring MVC中@Controller和@RestController的区别
Controller 和 RestController 是 Spring MVC 中用于处理 HTTP 请求的注解,它们有以下区别: 返回值处理方式: Controller 用于定义一个传统的 Spring MVC 控制器,它的方法通常返回视图名称或 ModelAndView 对象,由视图…...
Flink定制化功能开发,demo代码
前言: 这是一个Flink自定义开发的基础教学。本文将通过flink的DataStream模块API,以kafka为数据源,构建一个基础测试环境;包含一个kafka生产者线程工具,一个自定义FilterFunction算子,一个自定义MapFunctio…...

Edge浏览器入门
关于作者: CSDN内容合伙人、技术专家, 从零开始做日活千万级APP,带领团队单日营收超千万。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、商业化变现、人工智能等,希望大家多多支持。 目录 一、导读二、概览…...

Go语言的调度器
简介 Go语言的调度器是一个非常强大的工具,它可以帮助我们轻松地实现并发编程。调度器的工作原理是将多个协程映射到多个操作系统线程上,并根据协程的状态来决定哪个协程应该在哪个线程上运行。 调度器有两种主要策略: 协作式调度…...
Linux系统使用超详细(十)~vi/vim命令①
vi/vim命令有很多,其实只有少数的用法对于我们日常工作中起到了很大帮助,但是既然我选择梳理Linux的学习笔记,那么一定全力把自己的理解和学习笔记的内容认真整理汇总,内容或许有错误,还请发现的C友们发现了及时指出。…...

C语言实现双向链表
1.版本一 由于节点之间的连接变多 所以我们最好提前将前驱节点和后继节点用变量保存下来 以免等下在进行节点之间的指向时出错 #include <stdio.h> #include <stdlib.h> #include <stdbool.h> // 节点类 typedef struct Node {// 数据域int data;// 指针域…...
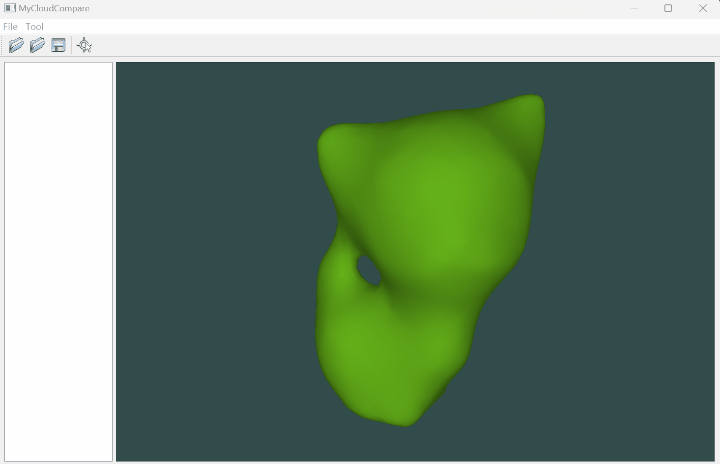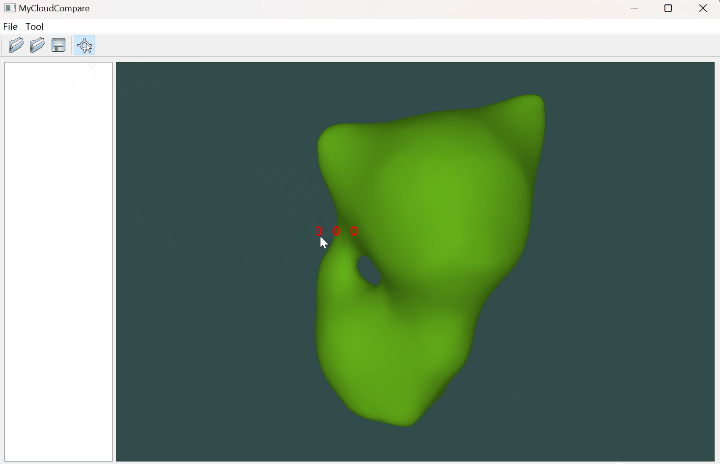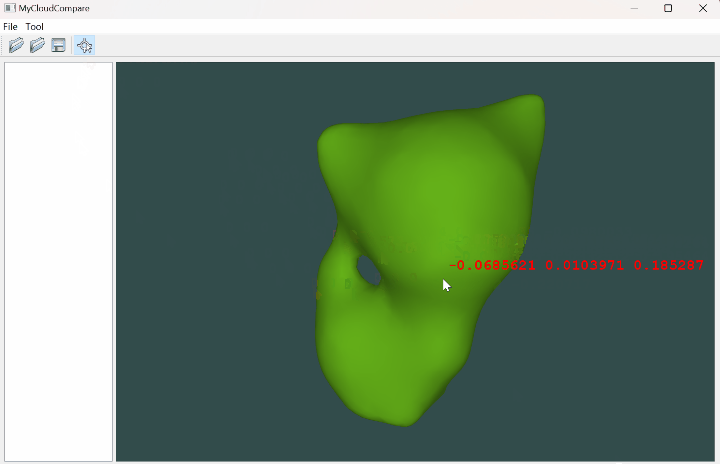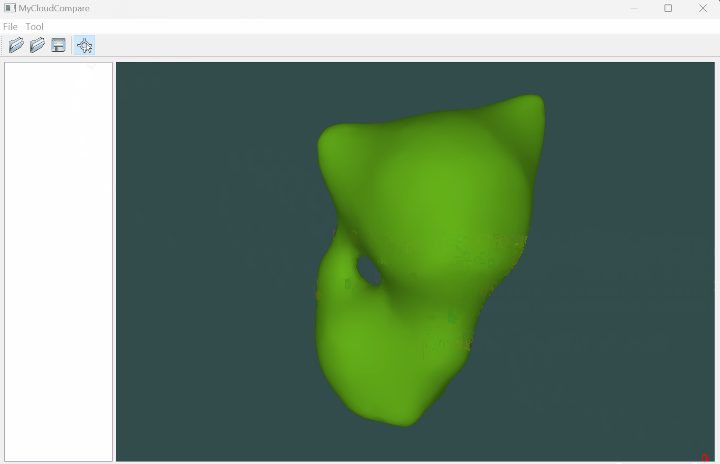
OpenGL 网格拾取坐标(Qt)
文章目录 一、简介二、代码实现三、实现效果参考资料一、简介 有时候我们希望通过鼠标来拾取某个网格中的坐标,这就涉及到一个很有趣的场景:光线投射,也就是求取一条射线与网格的交点,这里如果我们采用普通遍历网格中的每个面片的方式,当网格的面片数据量很大时计算效率就…...

GitHub高级搜索技巧
GitHub高级搜索技巧 in:name <关键字> 仓库名称带关键字查询 in:description <关键字> 仓库描述带关键字查询 in:readme <关键字> README文件带关键字查询 stars(fork): >() <数字> <关键字> star或fork数大于(或等于)指定数字的带关键字查…...
docker-compose安装HertzBeat赫兹跳动监控H3C交换机
前面我们用docker方式安装了HertzBeat,现在我们自己写个docker-compose.yml文件、创建文件直接docker-compose up -d直接启动运行 使用docker-compose需要先安装docker和docker-compose1、输入以下两段命令 mkdir 123 && cd 123 && mkdir data &a…...

NetSuite学习笔记 - 中心
一、什么是中心? 对于每个用户,NetSuite 会根据用户的指定角色显示一组可变的标签页面,称为中心。通俗来讲呢,NetSuite的中心其实就是我们常说的“导航菜单”。 只是在我过去常见的系统中,导航菜单一般都是固定的&am…...
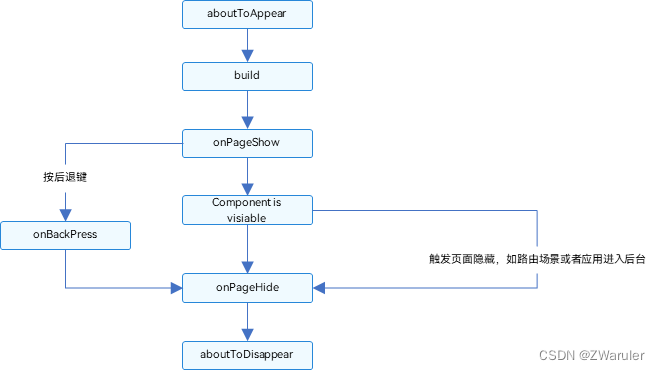
鸿蒙开发笔记(三):页面和自定义组件生命周期
先明确自定义组件和页面的关系: 自定义组件:Component装饰的UI单元,可以组合多个系统组件实现UI的复用。 页面:即应用的UI页面。可以由一个或者多个自定义组件组成,Entry装饰的自定义组件为页面的入口组件,…...
报名活动怎么做_小程序创建线上报名活动最详细攻略
报名活动怎么做:一篇让你掌握活动策划与营销的秘籍 在当今社会,无论是线上还是线下,活动已经成为企业营销和品牌推广的重要手段。但是,如何策划一场成功的活动呢?这篇文章将为你揭示活动策划与营销的秘籍,…...
Apache POI 导出Excel报表
大家好我是苏麟 , 今天聊聊Apache POI . Apache POI 介绍 Apache POI 是一个处理Miscrosoft Office各种文件格式的开源项目。简单来说就是,我们可以使用 POI 在 Java 程序中对Miscrosoft Office各种文件进行读写操作。 一般情况下,POI 都是用于操作 E…...
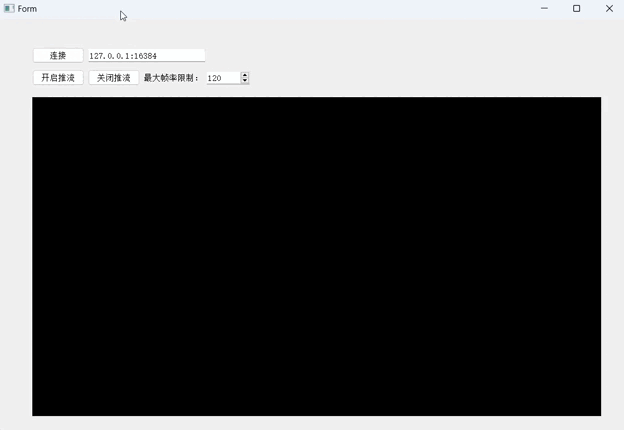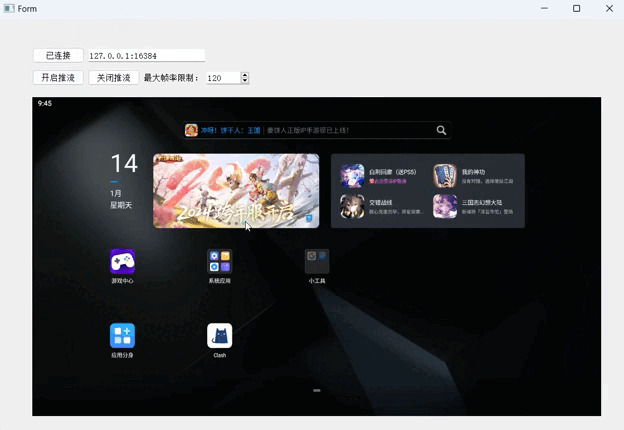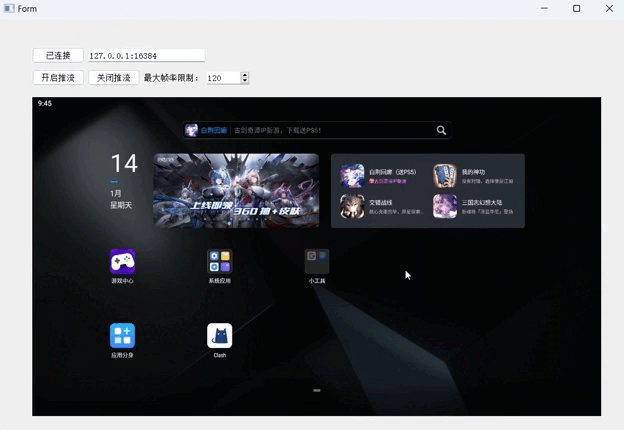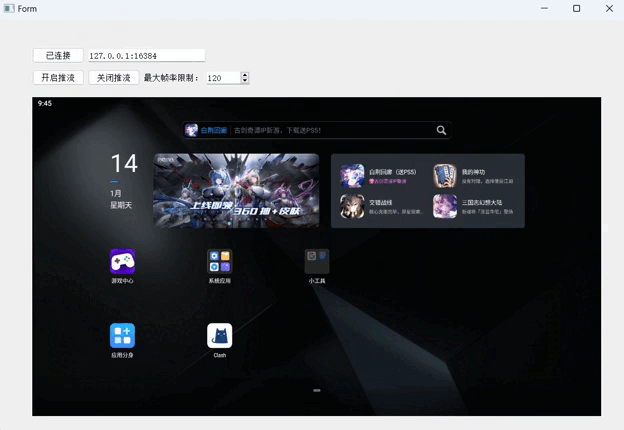
使用Qt连接scrcpy-server控制手机
Qt连接scrcpy-server 测试环境如何启动scrcpy-server1. 连接设备2. 推送scrcpy-server到手机上3. 建立Adb隧道连接4. 启动服务5. 关闭服务 使用QTcpServer与scrcpy-server建立连接建立连接并视频推流完整流程1. 开启视频推流过程2. 关闭视频推流过程 视频流的解码1. 数据包协议…...

debian12部署Gitea服务之二——部署git-lfs
Debian安装gitlfs: 先更新下软件包版本 sudo apt update 安装 sudo apt install git-lfs 验证是否安装成功 git lfs version cd到Gitea仓库目录下 cd /mnt/HuHDD/Git/Gitea/Repo/hu/testrepo.git 执行lfs的初始化命令 git lfs install客户机Windows端在官网下载并安装Git-Lfs 再…...

leetcode 1两数之和
题目 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺…...
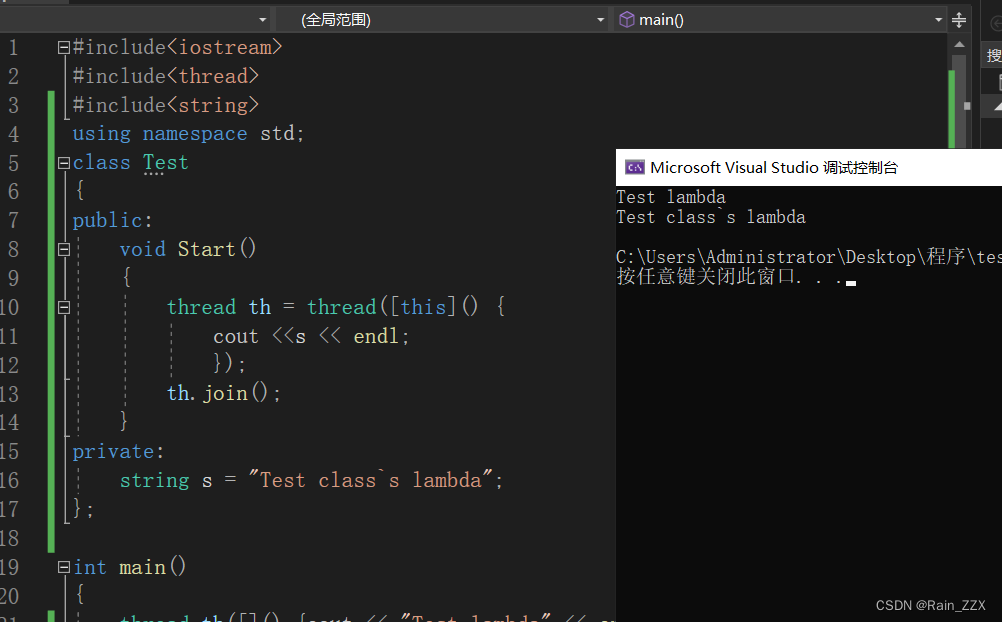
C++多线程学习[三]:成员函数作为线程入口
一、成员函数作为线程入口 #include<iostream> #include<thread> #include<string>using namespace std;class Mythread { public:string str;void Test(){cout << str << endl;} }; int main() {Mythread test;test.str "Test";thr…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
