数据结构实战:变位词侦测
文章目录
- 一、实战概述
- 二、实战步骤
- (一)逐个比较法
- 1、编写源程序
- 2、代码解释说明
- (1)函数逻辑解释
- (2)主程序部分
- 3、运行程序,查看结果
- 4、计算时间复杂度
- (二)排序比较法
- 1、编写源程序
- 2、代码解释说明
- (1) 函数逻辑解释
- (2)主程序部分
- 3、运行程序,查看结果
- 4、计算时间复杂度
- (三)计数比较法
- 1、编写源程序
- 2、代码解释说明
- (1)函数逻辑解释
- (2)主程序部分
- 3、运行程序,查看结果
- 4、计算时间复杂度
- (四)相互包含法
- 1、编写源程序
- 2、代码解释说明
- (1)函数逻辑解释
- (2)主程序部分
- 3、运行程序,查看结果
- 4、计算时间复杂度
- (五)强力法
- 三、实战总结
一、实战概述
-
本实战通过编写四个Python程序,分别采用逐个比较法、排序比较法、计数比较法和相互包含法来解决变位词检测问题。逐个比较法的时间复杂度为 O ( n 2 ) \text{O}(n^2) O(n2),虽然实现简单但效率较低;排序比较法则利用字符串排序后直接比较,时间复杂度为 O ( n l o g n ) \text{O}(n log n) O(nlogn),效率相对较高;计数比较法则统计字符出现次数进行对比,时间复杂度为 O ( n ) \text{O}(n) O(n),是四种方法中最高效的;而相互包含法则分别检查两个字符串中的字符是否完全包含对方,时间复杂度为 O ( n ∗ m ) \text{O}(n*m) O(n∗m)。
-
在实际应用中,针对不同的场景需求和输入规模,可选择合适的算法以达到时间和空间效率的最佳平衡。例如,在处理大规模字符串时,计数比较法更优;而在较小规模或对内存有限制的场景下,排序比较法可能是更好的选择。同时,强力法由于其极高的时间复杂度( n ! n! n!),不适用于实际问题求解。
二、实战步骤
(一)逐个比较法
1、编写源程序
- 编写Python程序 -
变位词侦测问题解法01-逐个比较法.py

'''
功能:变位词侦测问题解法01-逐个比较法
作者:华卫
日期:2024年01月13日
'''def anagramSolution1(s1, s2):stillOK = Trueif len(s1) != len(s2):stillOK = Falsealist = list(s2)pos1 = 0while pos1 < len(s1) and stillOK:pos2 = 0found = Falsewhile pos2 < len(alist) and not found:if s1[pos1] == alist[pos2]:found = Trueelse:pos2 = pos2 + 1if found:alist.pop(pos2)else:stillOK = Falsepos1 = pos1 + 1return stillOKstr1 = input('Input the first string: ')
str2 = input('Input the second string: ')
if anagramSolution1(str1, str2):print(str1, 'and', str2, 'are anagrams.')
else:print(str1, 'and', str2, 'are not anagrams.')
2、代码解释说明
- 这段代码实现了一个名为
anagramSolution1的函数,用于检测两个输入字符串(s1和s2)是否为变位词。
(1)函数逻辑解释
-
函数首先检查两个字符串的长度是否相等,如果不等,则直接返回False,表示它们不是变位词。
-
将第二个字符串
s2转换为字符列表alist,便于进行元素操作。 -
使用变量
pos1遍历第一个字符串s1的每个字符。a. 初始化一个布尔变量
found为False,用于记录当前字符是否在alist中找到。b. 对于
s1中的每个字符,使用pos2遍历alist,寻找匹配项。-
如果找到匹配项(即
s1[pos1] == alist[pos2]),将found设为True,并跳出内层循环。 -
否则,将
pos2加1继续搜索下一个字符。
c. 如果找到了匹配项,从
alist中移除该字符(alist.pop(pos2));否则,将stillOK设为False,表示无法构成变位词。d. 将
pos1递增,准备处理下一个字符。 -
-
当遍历完
s1的所有字符且stillOK仍为True时,说明s1与s2是变位词,函数返回True;否则返回False。
(2)主程序部分
-
通过
input()获取用户输入的两个字符串str1和str2。 -
调用
anagramSolution1(str1, str2)函数判断这两个字符串是否为变位词。 -
根据函数返回的结果输出相应的信息,如果两个字符串是变位词,则输出"str1 and str2 are anagrams.“,否则输出"str1 and str2 are not anagrams.”。
3、运行程序,查看结果
- 运行两次程序,第一次是同位词,第二次不是同位词
4、计算时间复杂度
-
此程序的时间复杂度为 O ( n 2 ) \text{O}(n^2) O(n2),其中n代表输入字符串s1和s2的长度(假设它们是等长的)。
-
首先检查两个字符串长度,时间复杂度为 O ( 1 ) \text{O}(1) O(1)。
-
将字符串s2转换为列表alist,时间复杂度为 O ( n ) \text{O}(n) O(n)。
-
使用两层循环进行逐个字符比较:
- 外层循环遍历字符串s1,次数为n,时间复杂度为 O ( n ) \text{O}(n) O(n)。
- 内层循环在每一轮外层循环中遍历alist寻找匹配项,最坏情况下需要遍历整个alist,次数也为n,因此内层循环的时间复杂度为 O ( n ) \text{O}(n) O(n)。
- 因此,总的时间复杂度为 O ( n ∗ n ) \text{O}(n*n) O(n∗n),即 O ( n 2 ) \text{O}(n^2) O(n2)。
-
此外,在内层循环找到匹配项后执行的
alist.pop(pos2)操作,虽然在Python中平均时间复杂度为 O ( n ) \text{O}(n) O(n),但在实际应用中(由于每次找到一个匹配项就移除一个元素),其对于整体时间复杂度的影响可以忽略不计,所以整体时间复杂度仍视为 O ( n 2 ) \text{O}(n^2) O(n2)。 -
T ( n ) = ∑ i = 1 n = n ( n + 1 ) 2 ≈ O ( n 2 ) \displaystyle \text{T}(n)=\sum_{i=1}^n=\frac{n(n+1)}{2}\approx \text{O}(n^2) T(n)=i=1∑n=2n(n+1)≈O(n2)
(二)排序比较法
1、编写源程序
- 编写Python程序 -
变位词侦测问题解法02-排序比较法.py
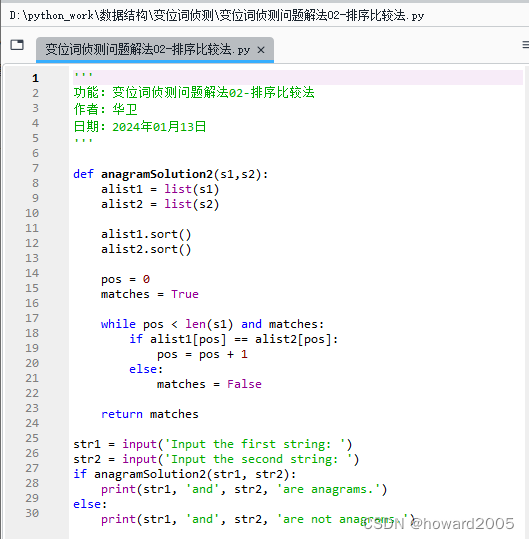
'''
功能:变位词侦测问题解法02-排序比较法
作者:华卫
日期:2024年01月13日
'''def anagramSolution2(s1,s2):alist1 = list(s1)alist2 = list(s2)alist1.sort()alist2.sort()pos = 0matches = Truewhile pos < len(s1) and matches:if alist1[pos] == alist2[pos]:pos = pos + 1else:matches = Falsereturn matchesstr1 = input('Input the first string: ')
str2 = input('Input the second string: ')
if anagramSolution2(str1, str2):print(str1, 'and', str2, 'are anagrams.')
else:print(str1, 'and', str2, 'are not anagrams.')
2、代码解释说明
- 这段代码实现了一个名为
anagramSolution2的函数,用于检测两个输入字符串(s1和s2)是否为变位词。
(1) 函数逻辑解释
-
首先将输入的两个字符串
s1和s2分别转换为字符列表alist1和alist2。 -
对这两个字符列表进行排序操作,排序后的列表中,相同的字符将会按照字典序排列到一起。
-
初始化一个变量
pos为0,表示当前比较的位置;同时初始化布尔值matches为True,用以记录是否所有对应位置的字符都匹配成功。 -
使用while循环遍历两个已排序的字符列表,直到遍历完其中一个列表或发现不匹配为止:
- 如果在相同位置上的字符相等(即
alist1[pos] == alist2[pos]),则将pos加1继续比较下一个字符。 - 否则,将
matches设置为False,跳出循环。
- 如果在相同位置上的字符相等(即
-
循环结束后,根据
matches的值判断两个字符串是否为变位词:- 若
matches为True,则说明原字符串s1和s2是变位词,返回True。 - 若
matches为False,则说明它们不是变位词,返回False。
- 若
(2)主程序部分
-
通过
input()获取用户输入的两个字符串str1和str2。 -
调用
anagramSolution2(str1, str2)函数判断这两个字符串是否为变位词。 -
根据函数返回的结果输出相应的信息,如果两个字符串是变位词,则输出"str1 and str2 are anagrams.“,否则输出"str1 and str2 are not anagrams.”。
3、运行程序,查看结果
- 运行两次程序,第一次是同位词,第二次不是同位词
4、计算时间复杂度
- 此程序的时间复杂度主要由两部分组成:
-
排序操作:对输入字符串
s1和s2转换成的字符列表alist1和alist2进行排序。Python内置的sort()方法采用Timsort算法,其平均时间复杂度为 O ( n l o g n ) \text{O}(n log n) O(nlogn),其中 n n n为列表长度(即字符串长度)。 -
遍历比较操作:在排序后的字符列表中,通过一个while循环逐个比较对应位置的字符是否相等,该过程的时间复杂度为 O ( n ) \text{O}(n) O(n)。
- 因此,整个程序的时间复杂度为 O ( n l o g n ) + O ( n ) = O ( n l o g n ) \text{O}(n log n) + \text{O}(n) = \text{O}(n log n) O(nlogn)+O(n)=O(nlogn),其中主要的时间消耗在于排序阶段。不过,在实际情况中,由于遍历比较阶段总是紧跟在排序阶段之后,并且只执行一次,所以整体的时间复杂度通常简记为 O ( n l o g n ) \text{O}(n log n) O(nlogn)。
(三)计数比较法
1、编写源程序
- 编写Python程序 -
变位词侦测问题解法03-计数比较法.py
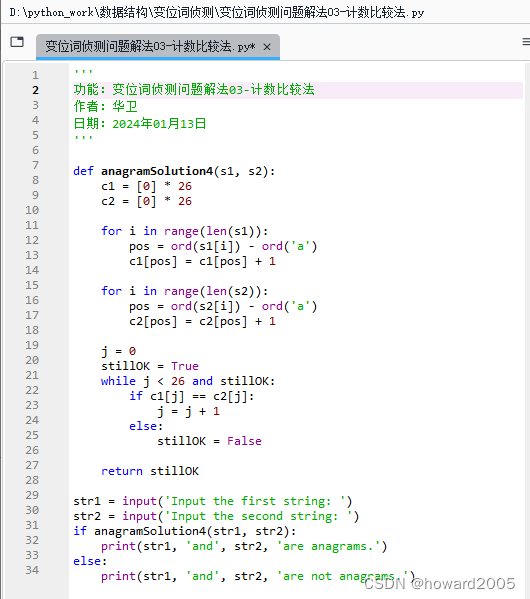
'''
功能:变位词侦测问题解法03-计数比较法
作者:华卫
日期:2024年01月13日
'''def anagramSolution4(s1, s2):c1 = [0] * 26c2 = [0] * 26for i in range(len(s1)):pos = ord(s1[i]) - ord('a')c1[pos] = c1[pos] + 1for i in range(len(s2)):pos = ord(s2[i]) - ord('a')c2[pos] = c2[pos] + 1j = 0stillOK = Truewhile j < 26 and stillOK:if c1[j] == c2[j]:j = j + 1else:stillOK = Falsereturn stillOKstr1 = input('Input the first string: ')
str2 = input('Input the second string: ')
if anagramSolution4(str1, str2):print(str1, 'and', str2, 'are anagrams.')
else:print(str1, 'and', str2, 'are not anagrams.')
2、代码解释说明
- 这段代码实现了一个名为
anagramSolution4的函数,用于检测两个输入字符串(s1和s2)是否为变位词。该方法采用计数比较法,统计每个字符串中各字符出现的次数,并进行比较。
(1)函数逻辑解释
-
初始化两个长度为26的计数列表
c1和c2,分别用于记录字符串s1和s2中小写字母的出现次数。这里假设输入字符串仅包含小写字母。 -
对于字符串
s1中的每一个字符:- 计算其在字母表中的位置,通过
ord(s1[i]) - ord('a')得到(将字符转换为其ASCII值并减去’a’的ASCII值)。 - 将对应位置的计数加1。
- 计算其在字母表中的位置,通过
-
同样对字符串
s2执行相同的操作,更新计数列表c2。 -
初始化一个变量
j为0,表示当前正在检查的小写字母的位置,以及一个布尔值stillOK,初始值为True,表示目前所有已检查的字符计数都相等。 -
使用while循环遍历26个小写字母,如果在对应的索引位置上
c1[j]与c2[j]相等,则继续检查下一个字母;否则,将stillOK设置为False,跳出循环。 -
循环结束后,根据
stillOK的值判断两个字符串是否为变位词:- 若
stillOK仍为True,说明原字符串s1和s2是变位词,返回True。 - 若
stillOK变为False,则说明它们不是变位词,返回False。
- 若
(2)主程序部分
-
通过
input()获取用户输入的两个字符串str1和str2。 -
调用
anagramSolution4(str1, str2)函数判断这两个字符串是否为变位词。 -
根据函数返回的结果输出相应的信息,如果两个字符串是变位词,则输出"str1 and str2 are anagrams.“,否则输出"str1 and str2 are not anagrams.”。
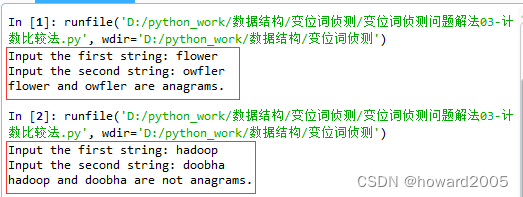
3、运行程序,查看结果
- 运行两次程序,第一次是同位词,第二次不是同位词
4、计算时间复杂度
-
此程序的时间复杂度为 O ( n ) \text{O}(n) O(n),其中 n n n表示输入字符串的长度。
-
在函数
anagramSolution4中,首先初始化了两个长度为26的列表c1和c2,时间复杂度为 O ( 1 ) \text{O}(1) O(1)。 -
然后对
s1中的每个字符进行遍历,计算其在字母表中的位置并增加相应计数,循环次数为n(假设字符串仅包含小写字母),时间复杂度为 O ( n ) \text{O}(n) O(n)。 -
同样地,对
s2中的每个字符执行相同的操作,时间复杂度也为 O ( n ) \text{O}(n) O(n)。 -
最后,通过一个while循环比较两个计数列表是否相等,循环最多会进行26次(对于所有可能的小写字母),因此这一部分的时间复杂度是 O ( 1 ) \text{O}(1) O(1)级别的。
-
-
综合上述步骤,整个程序的主要时间消耗在于遍历字符串并统计字符出现次数的部分,故总时间复杂度为 O ( n ) \text{O}(n) O(n)。同时,由于空间上只使用了固定大小的计数数组,所以空间复杂度为 O ( 1 ) \text{O}(1) O(1)。
(四)相互包含法
1、编写源程序
- 编写Python程序 -
变位词侦测问题解法04-相互包含法.py
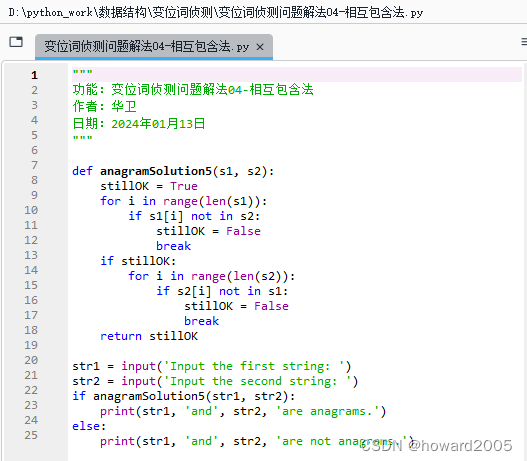
"""
功能:变位词侦测问题解法04-相互包含法
作者:华卫
日期:2024年01月13日
"""def anagramSolution5(s1, s2):stillOK = Truefor i in range(len(s1)):if s1[i] not in s2:stillOK = Falsebreakif stillOK:for i in range(len(s2)):if s2[i] not in s1:stillOK = Falsebreakreturn stillOKstr1 = input('Input the first string: ')
str2 = input('Input the second string: ')
if anagramSolution5(str1, str2):print(str1, 'and', str2, 'are anagrams.')
else:print(str1, 'and', str2, 'are not anagrams.')
2、代码解释说明
- 这段代码实现了一个名为
anagramSolution5的函数,用于检测两个输入字符串(s1和s2)是否为变位词。该方法采用了相互包含法,即检查一个字符串中的每个字符是否都出现在另一个字符串中。
(1)函数逻辑解释
-
初始化一个布尔变量
stillOK为True,表示在没有发现不匹配字符的情况下,两个字符串可能是变位词。 -
使用一个for循环遍历字符串
s1中的每个字符:- 如果当前字符不在字符串
s2中,则将stillOK设为False,并使用break语句跳出循环。这意味着s1中存在s2中没有的字符,因此它们不是变位词。
- 如果当前字符不在字符串
-
当遍历完
s1后,如果stillOK仍为True,则继续对字符串s2进行相同的操作:- 用另一个for循环遍历
s2中的每个字符。 - 如果当前字符不在字符串
s1中,则将stillOK设为False,并同样使用break语句跳出循环。这意味着s2中也存在s1中没有的字符,因此它们不是变位词。
- 用另一个for循环遍历
-
在完成所有检查后,返回
stillOK的值。若为True,说明两个字符串是变位词;否则,它们不是变位词。
(2)主程序部分
-
通过
input()获取用户输入的两个字符串str1和str2。 -
调用
anagramSolution5(str1, str2)函数判断这两个字符串是否为变位词。 -
根据函数返回的结果输出相应的信息,如果两个字符串是变位词,则输出"str1 and str2 are anagrams.“,否则输出"str1 and str2 are not anagrams.”。
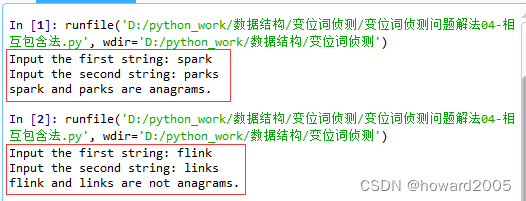
3、运行程序,查看结果
- 运行两次程序,第一次是同位词,第二次不是同位词
4、计算时间复杂度
-
此程序的时间复杂度为 O ( n ∗ m ) \text{O}(n*m) O(n∗m),其中 n n n和 m m m分别为输入字符串s1和s2的长度。
-
在函数
anagramSolution5中,首先遍历字符串s1,对每个字符执行一次查找操作(即s1[i] not in s2),这需要在字符串s2中进行线性搜索。最坏情况下,对于每个字符都需要遍历整个s2,因此这部分时间复杂度为 O ( m ) \text{O}(m) O(m)。 -
如果
s1中的所有字符都在s2中找到,则继续遍历字符串s2,再次对每个字符执行查找操作(即s2[i] not in s1)。同样地,这部分在最坏情况下也具有 O ( n ) \text{O}(n) O(n)的时间复杂度。
-
-
因此,总时间复杂度为这两部分之和,即 O ( n + m ) \text{O}(n+m) O(n+m),由于两者均与输入字符串的长度相关且相互独立,我们可以将其简化为 O ( n ∗ m ) \text{O}(n*m) O(n∗m),表示随着两个字符串长度同时增加时,程序运行时间的增长趋势。
(五)强力法
- 强力法采用穷尽所有可能性的方式来处理问题。对于长度为n的字符串s1,全排列得到所有字符串,然后去看s2是否出现在s1全排列后构成的字符串列表里。 T ( n ) = n × ( n − 1 ) × ( n − 2 ) × . . . . × 2 × 1 = n ! T(n)=n\times(n-1)\times(n-2)\times....\times2\times1= n! T(n)=n×(n−1)×(n−2)×....×2×1=n!, n ! n! n!跑得比 2 n 2^n 2n还要快得多,比如 20 ! = 2432902008176640000 20!= 2432902008176640000 20!=2432902008176640000。如果每秒钟处理一种可能性,那么要花 77 , 146 , 816 , 596 77,146,816,596 77,146,816,596年才能遍历整个列表。显然不是一个好的解决方案。
三、实战总结
- 实战中,我们运用四种不同策略检测变位词:逐个比较法( O ( n 2 ) \text{O}(n^2) O(n2))、排序比较法( O ( n l o g n ) \text{O}(n log n) O(nlogn))、计数比较法( O ( n ) \text{O}(n) O(n))和相互包含法( O ( n ∗ m ) \text{O}(n*m) O(n∗m))。其中,计数比较法效率最高,适合大规模字符串;排序比较法则在小规模数据或对内存有限制时适用。通过实践对比,理解并掌握了针对不同场景选择合适算法的重要性。
相关文章:

数据结构实战:变位词侦测
文章目录 一、实战概述二、实战步骤(一)逐个比较法1、编写源程序2、代码解释说明(1)函数逻辑解释(2)主程序部分 3、运行程序,查看结果4、计算时间复杂度 (二)排序比较法1…...
C++核心编程之类和对象---C++面向对象的三大特性--多态
目录 一、多态 1. 多态的概念 2.多态的分类: 1. 静态多态: 2. 动态多态: 3.静态多态和动态多态的区别: 4.动态多态需要满足的条件: 4.1重写的概念: 4.2动态多态的调用: 二、多态 三、多…...
基于PyQT的图片批处理系统
项目背景: 随着数字摄影技术的普及,人们拍摄和处理大量图片的需求也越来越高。为了提高效率,开发一个基于 PyQt 的图片批处理系统是很有意义的。该系统可以提供一系列图像增强、滤波、水印、翻转、放大缩小、旋转等功能,使用户能够…...

vscode文件配置
lanuch.json {"version": "0.2.0","configurations": [{"name": "(gdb) 启动","type": "cppdbg","request": "launch",// "program": "输入程序名称,例…...

C++学习笔记——SLT六大组件及头文件
目录 一、C中STL(Standard Template Library) 二、 Gun源代码开发精神 三、 实现版本 四、GNU C库的头文件分布 bits目录 ext目录 backward目录 iostream目录 stdexcept目录 string目录 上一篇文章: C标准模板库(STL&am…...

Spring之AOP源码(二)
书接上文 文章目录 一、简介1. 前文回顾2. 知识点补充 二、ProxyFactory源码分析1. ProxyFactory2. JdkDynamicAopProxy3. ObjenesisCglibAopProxy 三、 Spring AOP源码分析 一、简介 1. 前文回顾 前面我们已经介绍了AOP的基本使用方法以及基本原理,但是还没有涉…...
)
VS code console.log快捷键设置 :console.log(‘n>>>‘,n)
vscode设置log快捷显示: 一、打开 VS Code,并进入菜单栏选择 “文件”(File)-> “首选项”(Preferences)-> “用户代码片段”(User Snippets)。 二、在弹出的下拉菜单中选择 …...
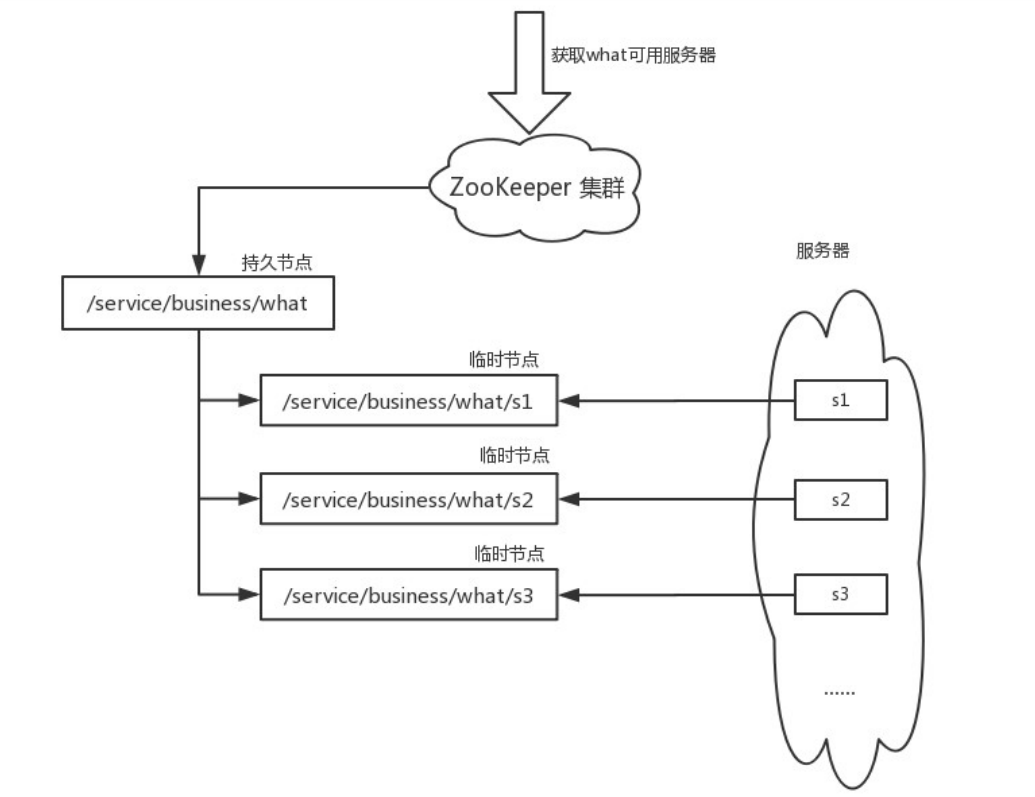
ZooKeeper 简介
1、概念介绍 ZooKeeper 是一个开放源码的分布式应用程序协调服务,为分布式应用提供一致性服务的软件,由雅虎创建,是 Google Chubby 的开源实现,是 Apache 的子项目,之前是 Hadoop 项目的一部分,使用 Java …...
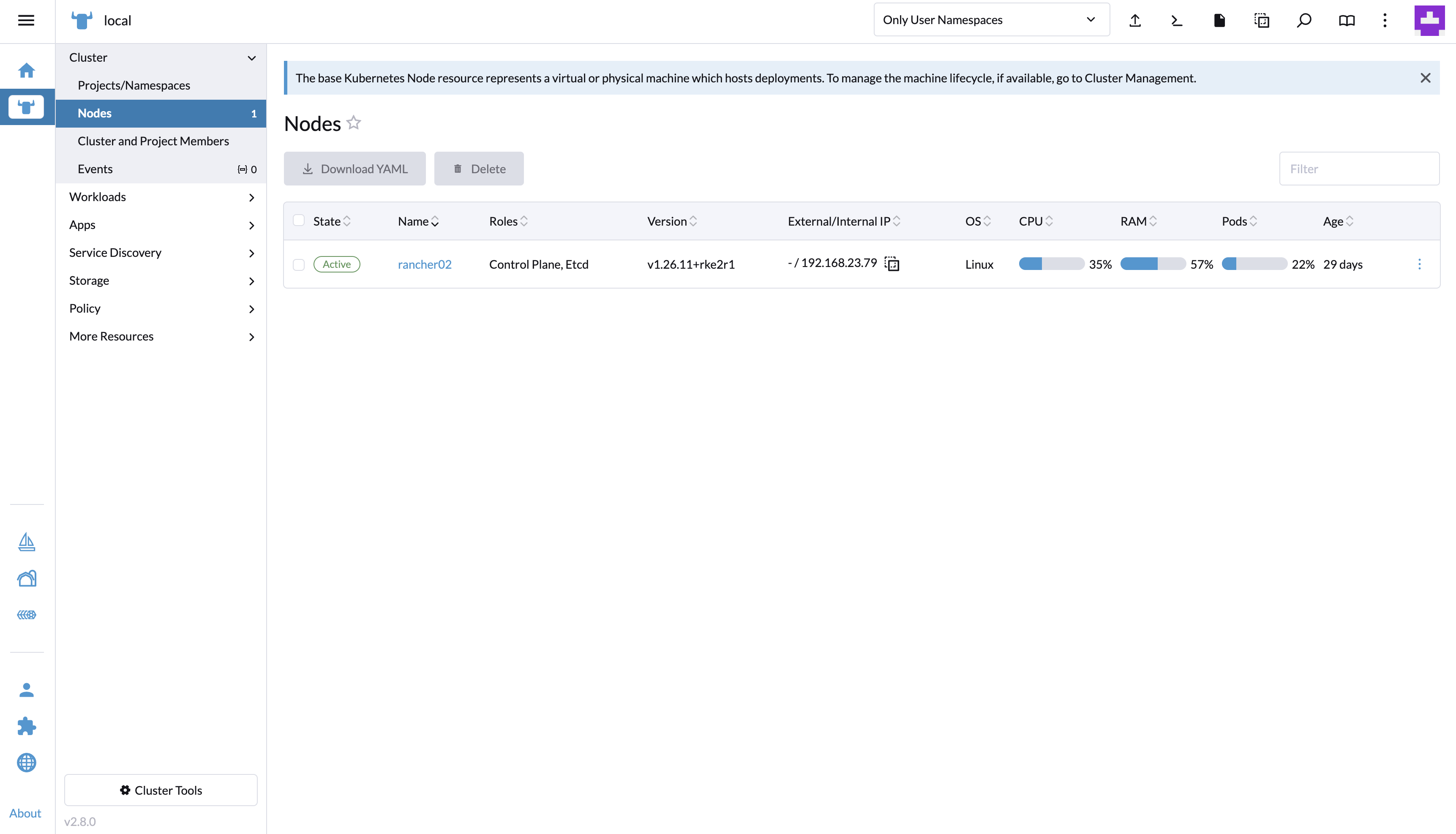
rke2 Online Deploy Rancher v2.8.0 latest (helm 在线部署 rancher v2.8.0)
文章目录 1. 简介2. 预备条件3. 安装 helm4. 安装 cert-manager4.1 yaml 安装4.2 helm 安装 5. 安装 rancher6. 验证7. 界面预览 1. 简介 Rancher 是一个 Kubernetes 管理工具,让你能在任何地方和任何提供商上部署和运行集群。 Rancher 可以创建来自 Kubernetes 托…...

k8s实战从入门到上天系列第一篇:K8s微服务实战内容开篇介绍
前言 我们使用开源ruoyi微服务基本使用,基于基本的微服务实践。我们来讲解k8s的实战内容。 第一章:开源ruoyi微服务简介基本使用 第二章:k8s基本知识回顾、k3s集群搭建和基本使用 第三章:微服务镜像构建 第四章:中间件…...
统一网关 Gateway【微服务】
文章目录 1. 前言2. 搭建网关服务3. 路由断言工厂4. 路由过滤器4.1 普通过滤器4.2 全局过滤器4.3 过滤器执行顺序 5. 跨域问题处理 1. 前言 通过前面的学习我们知道,通过 Feign 就可以向指定的微服务发起 http 请求,完成远程调用。但是这里有一个问题&am…...

【征服redis1】基础数据类型详解和应用案例
博客计划 ,我们从redis开始,主要是因为这一块内容的重要性不亚于数据库,但是很多人往往对redis的问题感到陌生,所以我们先来研究一下。 本篇,我们先看一下redis的基础数据类型详解和应用案例。 1.redis概述 以mysql为…...

【WPF.NET开发】WPF中的XAML资源
本文内容 使用 XAML 中的资源静态和动态资源静态资源动态资源样式、DataTemplate 和隐式键 资源是可以在应用中的不同位置重复使用的对象。 资源的示例包括画笔和样式。 本概述介绍如何使用 Extensible Application Markup Language (XAML) 中的资源。 你还可以使用代码创建和…...
)
ChatGPT 淘金潮(全)
原文:The ChatGPT GoldRush 译者:飞龙 协议:CC BY-NC-SA 4.0 一、ChatGPT 简介 什么是 ChatGPT? ChatGPT 是由 OpenAI 基于 GPT-4 架构创建的大型语言模型。它旨在理解和回应自然语言文本输入,使得可以与机器进行对话…...
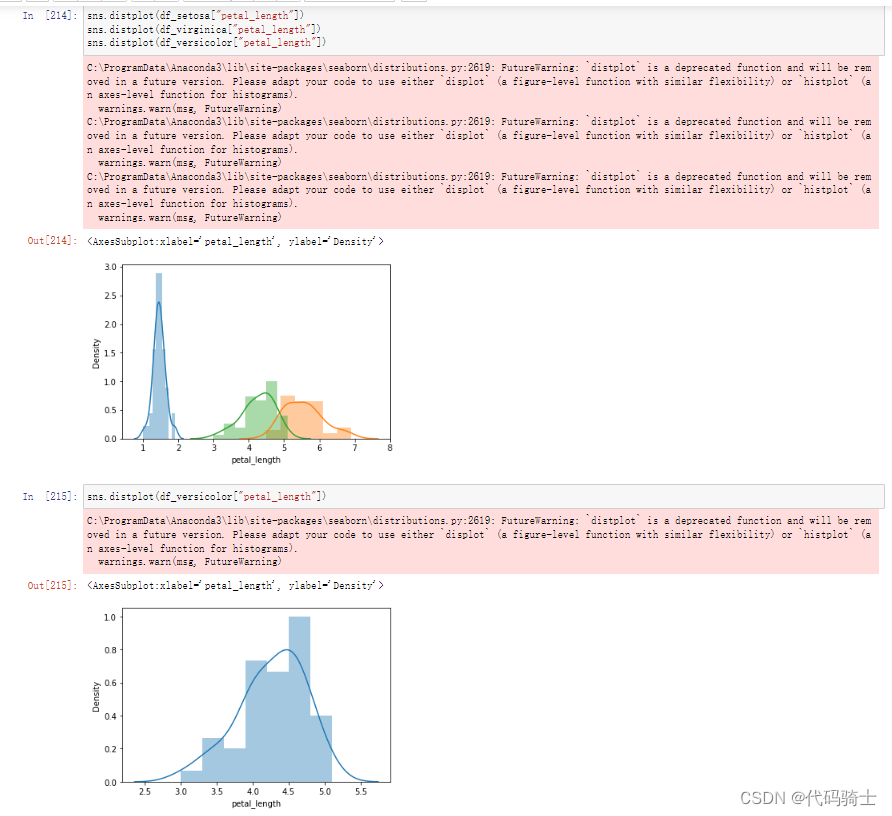
【零基础入门Python数据分析】Anaconda3 JupyterNotebookseaborn版
目录 一、安装环境 python介绍 anaconda介绍 jupyter notebook介绍 anaconda3 环境安装 解决JuPyter500:Internal Server Error问题-CSDN博客 Jupyter notebook快捷键操作大全 二、Python基础入门 数据类型与变量 数据类型 变量及赋值 布尔类型与逻辑运算…...

C++面试:单例模式、工厂模式等简单的设计模式 创建型、结构型、行为型设计模式的应用技巧
理解和能够实现基本的设计模式是非常重要的。这里,我们将探讨两种常见的设计模式:单例模式和工厂模式,并提供一些面试准备的建议。 目录 单例模式 (Singleton Pattern) 工厂模式 (Factory Pattern) 面试准备 1. 理解设计模式的基本概念…...

Oracle JDK 8 中的 computeIfAbsent 方法及实践
Java 8 引入了一系列新特性,其中之一是对 Map 接口的增强,其中包括了 computeIfAbsent 方法。这个方法为处理映射提供了一种便捷而强大的方式,允许在键不存在或对应的值为 null 时,动态计算新的值并将其放入映射。在本篇博客中&am…...
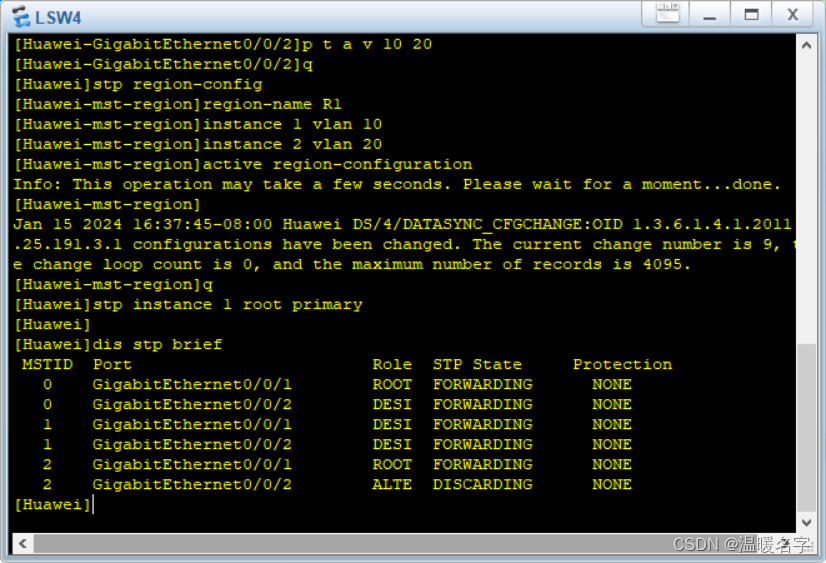
华为设备vlan下配置MSTP,STP选举
核心代码,不同实例,承载不同流量,为每个实例设置一个根网桥达到分流的效果 stp region-config //进入stp区域的设置 region-name R1 //区域命名为R1 instance 1 vlan 10 …...
函数的用法,高级!)
案例学Python:filter()函数的用法,高级!
大家好,这里是程序员晚枫,又来分享有用的Python知识了。 Python之所以好用,是因为有大量用于科学计算的内置函数和第三方库。用好这些第三方库,可以显著提高我们编程的速度和质量。 今天我们一起来看一下Python中一个重要的内置…...

jmeter--7.BeanShell
目录 1. beanshell常用语法 1.1 log:日志写入 1.2 vars:设置和引用局部变量(同线程组) 1.3 props:设置和引用全局变量(跨线程组) 1.4 prev:获取前一个请求返回的信息 2. beans…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
