【图形学】探秘图形学奥秘:DDA与Bresenham算法的解密与实战

🌈个人主页:Sarapines Programmer
🔥 系列专栏:《图形学 | 图像解码》
⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。

目录
🌌1. 初识模式识别
🌌2. 开发环境的使用及基本图形生成
🌍2.1 开发环境及实现
🌍2.2 实验目的
🌍2.3 实验要求
🌍2.4 实验原理
🌕2.4.1 DDA算法画直线
🌕2.4.2 Bresenham算法画直线
🌕2.4.3 DDA算法画圆
🌕2.4.4 Bresenham算法画圆
🌍2.5 实验步骤
🌕2.5.1 DDA算法代码实现画直线
🌕2.5.2 Breasenham 算法实现画直线
🌕2.5.3 DDA算法代码实现画圆
🌕2.5.4 Breasenham算法代码实现画圆
🌍2.6 研究体会
📝总结
🌌1. 初识模式识别
图形学技术是一门涉及计算机图形和图像处理的学科,其目标是通过算法和数学模型来创建、处理和呈现图形和图像。这项技术的应用范围非常广泛,涵盖了许多领域,包括计算机游戏、虚拟现实、计算机辅助设计(CAD)、医学图像处理、动画制作等。
以下是图形学技术的一些关键方面:
图形生成和渲染: 图形学技术用于生成和呈现视觉图像。这包括三维图形的创建、光照、阴影、颜色和纹理等方面的处理,以产生逼真的图形。
计算机辅助设计(CAD): 在工程学和设计领域,图形学技术被广泛用于创建和编辑数字化的设计图纸,促进设计过程的可视化和交互。
计算机游戏和虚拟现实: 图形学技术是游戏开发和虚拟现实领域的核心。它用于创建游戏中的角色、场景、特效以及虚拟现实环境,提供沉浸式的视觉体验。
医学图像处理: 在医学领域,图形学技术被用于处理和呈现医学图像,如CT扫描、MRI等,以协助医生进行诊断和手术规划。
动画制作: 图形学技术是制作动画的关键。通过在计算机上生成图形帧并进行渲染,动画制作得以实现。
图像处理: 图形学技术也包括对静态图像的处理,如图像编辑、滤镜应用、图像合成等。
在图形学技术的发展中,硬件加速、实时渲染、虚拟现实和增强现实等方面的创新不断推动着图形学的前沿。这门技术为数字世界的可视化和交互提供了强大的工具和方法。
🌌2. 开发环境的使用及基本图形生成
🌍2.1 开发环境及实现
- 语言: C++
- 平台: Microsoft Visual Studio 2022
🌍2.2 实验目的
- 熟悉开发环境。
- 生成基本图形如直线和二次曲线。
- 掌握计算机生成直线以及修改直线属性的方法。
🌍2.3 实验要求
- 熟悉 Microsoft Visual Studio 2022 开发环境。
- 使用 DDA 算法和 Bresenham 算法分别生成直线和圆。
🌍2.4 实验原理
🌕2.4.1 DDA算法画直线
DDA是数字微分分析式(Digital Differential Analyzer)的缩写。已知直线两端点(x1,y1)、(x2,y2),则斜率m为:
m = (y2-y1)/(x2-x1)= Dx/Dy;
直线中的每一点坐标都可以由前一点坐标变化一个增量(Dx, Dy)而得到,垠)育v1["vI~5,L,`?!_[d即表示为递归式:
xi+1=xi+Dx yi+1=yi+Dy
递归式的初值为直线的起点(x1, y1),这样,就可以用加法来生成一条直线。
🌕2.4.2 Bresenham算法画直线
本算法由Bresenham在1965年提出。设直线从起点(x1, y1)到终点(x2, y2)。直线可表示为方程y=mx+b。其中
b = y1 - m * x1,
m = (y2-y1)/(x2-x1)=dy/dx
我们的讨论先将直线方向限于1a象限在这种情况下,当直线光栅化时,x每次都增加1个单元,即
xi+1=xi+1。而y的相应增加应当小于1。为了光栅化,yi+1只可能选择如下两种位置之一。
yi+1的位置选择yi+1=yi 或者 yi+1=yi+1。选择的原则是看精确值y与yi及yi+1的距离d1及d2的大小而定。计算式为:
y=m(xi+1)+b
d1=y-yi
d2=yi+1-y
如果d1-d2>0,则yi+1=yi+1,否则yi+1=yi。因此算法的关键在于简便地求出d1-d2的符号。将式(2.1.1)、(2.1.2)、(2.1.3)代入d1-d2,得
d1-d2=2y-2yi-1=2(dy/dx) (xi+1)-2yi+2b-1
用dx乘等式两边,并以Pi=dx(d1-d2)代入上述等式,得
Pi=2xidy-2yidx+2dy+dx(2b-1)
d1-d2是我们用以判断符号的误差。由于在1a象限,dx总大于0,所以Pi仍旧可以用作判断符号的误差。Pi-1为:
Pi+1=Pi+2dy-2dx(yi+1-yi)
误差的初值P1,可将x1, y1,和b代入式(2.1.4)中的xi, yi而得到:
P1=2dy-dx
综述上面的推导,第1a象限内的直线Bresenham算法思想如下:
1.画点(x1, y2); dx=x2-x1; dy=y2-y1;
计算误差初值P1=2dy-dx; i=1;
2.求直线的下一点位置:
xi+1=xi+1;
if Pi>0 则yi+1=yi+1;
否则yi+1=yi;
3.画点(xi+1, yi-1);
4.求下一个误差Pi+1;
if Pi>0 则Pi+1=Pi+2dy-2dx;
否则Pi+1=Pi+2dy;
5.i=i+1; if i<dx+1则转2;否则结束。
🌕2.4.3 DDA算法画圆
假定某点Pi(xi, yi)已经是该圆弧上最接近实际圆弧的点,那么Pi的下一个点只可能是正右方的P1或右下方的P2两者之一
构造判别函数:
F(x, y)= x2 + y2 – R2
当F(x, y)= 0,表示点在圆上,当F(x, y)> 0,表示点在圆外,当F(x, y)< 0,表示点在圆内。如果M是P1和P2的中点,则M的坐标是(xi + 1, yi – 0.5),当F(xi + 1, yi – 0.5)< 0时,M点在圆内,说明P1点离实际圆弧更近,应该取P1作为圆的下一个点。同理分析,当F(xi + 1, yi – 0.5)> 0时,P2离实际圆弧更近,应取P2作为下一个点。当F(xi + 1, yi – 0.5)= 0时,P1和P2都可以作为圆的下一个点,算法约定取P2作为下一个点。
现在将M点坐标(xi + 1, yi – 0.5)带入判别函数F(x, y),得到判别式d:
d = F(xi + 1, yi – 0.5)= (xi + 1)2 + (yi –0.5)2 – R2
若d < 0,则取P1为下一个点,此时P1的下一个点的判别式为:
展开后将d带入可得到的递推关系:d’ = d + 2xi + 3
若d > 0,则取P2为下一个点,此时P2的下一个点的判别式为:
d’ = F(xi + 2, yi – 1.5)= (xi + 2)2 + (yi –1.5)2 – R
展开后将d带入可得到判别式的递推关系:d’ = d + 2(xi - yi) + 5
特别的,在第一个象限的第一个点(0, R)时,可以推倒出判别式d的初始值d0:
d0 = F(1, R – 0.5) = 1 – (R – 0.5)2 –R2 = 1.25 – R
🌕2.4.4 Bresenham算法画圆
Bresenham算法画圆生成算法思路如下:
①求误差初值,p0=3- 2r,i=1,画点(0,r)
②求下一个点的y坐标,其中xi+1=xi+1,如果pi<0则yi+1=yi,否则yi+1=yi-1
③画点(xi+1,yi+1)
④计算下一个误差,如果pi<0则pi+1=pi+4xi+6,否则pi+1=pi+4(xi-yi)+10
⑤i=i+1,如果x=y则结束,否则返回步骤②。
🌍2.5 实验步骤
(1) 在Microsoft Visual Studio 2022环境下创建名为BmpRead的MFC应用程序工程(单文档)
(2)编程实现DDA算法和算法画直线,同时利用两种算法画圆。
🌕2.5.1 DDA算法代码实现画直线
#include <gl\glut.h>
#include <math.h>
#include <stdio.h>
#include <Windows.h>
#include <conio.h>
#include <easyx.h>void DDA(int X0, int Y0, int Xn, int Yn)
{int dx = Xn - X0;int dy = Yn - Y0;int steps, direction;float xIncrement, yIncrement;float x = X0, y = Y0;if (abs(dx) > abs(dy)){steps = abs(dx);direction = 0;}else{steps = abs(dy);direction = 1;}xIncrement = float(dx) / float(steps);yIncrement = float(dy) / float(steps);//画点glBegin(GL_POINTS);for (int k = 0; k <= steps; ++k){if (direction == 0){glVertex2i(int(x), int(y + 0.5));}else{glVertex2i(int(x + 0.5), int(y));}x += xIncrement;y += yIncrement;}glEnd();
}void display()
{glClear(GL_COLOR_BUFFER_BIT);DDA(0, 0, 800, 1000);//调用函数glFlush();
}
void draw_pixel(int ix, int iy)
{glBegin(GL_POINTS);glVertex2i(ix, iy);glEnd();
}void myinit()
{glClearColor(1.0, 0.8, 1.0, 1.0);glColor3f(0.0, 0.5, 0.5);glPointSize(1.0);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(0.0, 1000.0, 0.0, 1000.0);
}
int main(int argc, char** argv)
{glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowSize(600, 500);glutInitWindowPosition(150.0, 150.0);glutCreateWindow("DDA画直线");glutDisplayFunc(display);myinit();glutMainLoop();
}
运行结果:

🌕2.5.2 Breasenham 算法实现画直线
#include <gl\glut.h>
#include <math.h>
#include <stdio.h>
#include <Windows.h>
#include <conio.h>
#include <easyx.h>void Bresenham(int x0, int y0, int x1, int y1) {void draw_pixel(int, int);int dx = abs(x1 - x0), dy = abs(y1 - y0), p = 2 * dy - dx;int Dy2 = 2 * dy, Dx2 = 2 * dy - 2 * dx;int x, y;if (x0 > x1) {x = x1; y = y1;x1 = x0;}else {x = x0;y = y0;}draw_pixel(x, y);while (x < x1) {x++;if (p < 0)p += Dy2;else {y++;p += Dx2;draw_pixel(x, y);}}
}void display()
{glClear(GL_COLOR_BUFFER_BIT);Bresenham(0, 0, 800, 800);//调用函数glFlush();
}
void draw_pixel(int ix, int iy)
{glBegin(GL_POINTS);glVertex2i(ix, iy);glEnd();
}void myinit()
{glClearColor(1.0, 0.8, 1.0, 1.0);glColor3f(0.0, 0.5, 0.5);glPointSize(1.0);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(0.0, 1000.0, 0.0, 1000.0);
}
int main(int argc, char** argv)
{glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowSize(600, 500);glutInitWindowPosition(150.0, 150.0);glutCreateWindow("Bresenham算法画直线");glutDisplayFunc(display);myinit();glutMainLoop();
}
运行结果:

🌕2.5.3 DDA算法代码实现画圆
#include<iostream>
#include<graphics.h>
#include<conio.h>
#include<time.h>
#include<math.h>
#include<stdlib.h>
#include<stdio.h>
using namespace std;/*中点画圆*/
void MidpointCircle(int x0, int y0, int r, int color)
{int x = 0, y = r;float d = 5.0 / 4 - r;while (x <= y) {putpixel(x0 + x, y0 + y, color);putpixel(x0 + x, y0 - y, color);putpixel(x0 - x, y0 + y, color);putpixel(x0 - x, y0 - y, color);putpixel(x0 + y, y0 + x, color);putpixel(x0 + y, y0 - x, color);putpixel(x0 - y, y0 + x, color);putpixel(x0 - y, y0 - x, color);if (d < 0)d += x * 2.0 + 3;else {d += 2.0 * (x - y) + 5; y--;}x++;}
}void main()
{int x0, y0, x1, y1;initgraph(640, 480);setbkcolor(YELLOW);cleardevice();MidpointCircle(300, 200, 90, BLACK);_getch();closegraph();
}运行结果:

🌕2.5.4 Breasenham算法代码实现画圆
#include <GL/glut.h>
#include<math.h>
#include<iostream>
#include <easyx.h>
using namespace std;
GLfloat pointsize = 1.0f;
void Bresenham(int x0,int y0,GLint R) {int x1 = x0, y1 = y0;GLint a = 0;GLint y = (int)(R * 1.0 / (sqrt(2)));GLfloat d0 = 1.25 - R;GLfloat d;glPointSize(pointsize);GLint cx = 0, cy = R;glVertex2i(0, 0);while (a <= y) {glVertex2i(x1+a, y1+cy);glVertex2i(x1-a, y1-cy);glVertex2i(x1-a, y1+cy);glVertex2i(x1+a, y1-cy);glVertex2i(x1+cy,y1-a);glVertex2i(x1-cy,y1-a);glVertex2i(x1-cy, y1+a);glVertex2i(x1+cy, y1+a);a++;if (d0 <= 0) {d0 = d0 + 2 * a + 3;cy = cy;}else {d0 = d0 + 2 * (a - cy) + 5;cy = cy - 1;}}}void display()
{glClearColor(1.0, 0.8, 1.0, 1.0);glClear(GL_COLOR_BUFFER_BIT);glColor3f(0.0, 0.0f, 0.0f);glBegin(GL_POINTS);Bresenham(0,100,100); //调用函数glEnd();glFlush();
}
void draw_pixel(int ix, int iy)
{glBegin(GL_POINTS);glVertex2i(ix, iy);glEnd();
}void myinit()
{glClearColor(1.0, 0.8, 1.0, 1.0);glColor3f(0.0, 0.5, 0.5);glPointSize(1.0);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(0.0, 1000.0, 0.0, 1000.0);
}int main(int argc, char** argv)
{glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowPosition(100, 100);glutInitWindowSize(600, 600);glutCreateWindow("Breasenham算法画圆");glClearColor(1.0, 1.0, 1.0, 1.0);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(-500.0, 500.0, -500.0, 500.0);glutDisplayFunc(display);glutMainLoop();return 0;
}运行结果:

🌍2.6 研究体会
-
实验环境配置和头文件安装: 通过本次实验,我成功完成了所需的环境配置,并使用EasyX安装了相应的头文件。在Visual Studio 2022开发平台中,我顺利进行了C++编程,这包括了配置开发环境、安装必要的库和头文件等步骤。这为后续的图形学实验提供了一个稳定的基础。
-
DDA算法和Bresenham算法的实现与比较: 在实验中,我分别实现了DDA算法和Bresenham算法用于生成直线和圆。我对这两种算法的效率和精度有了更深刻的理解。Bresenham算法相较于DDA算法在速度上更快,因为它避免了直线斜率的计算和浮点数运算,只使用整数。然而,DDA算法在精度上更高,因为它使用浮点数运算,但可能不如Bresenham算法快速。了解了它们的特点,我能够在选择算法时更好地权衡速度和精度。
-
Visual Studio 2022开发平台和函数库的使用: 在实验中,我发现之前可用的
getch()函数需要替换为_getch()。通过查询,我了解到带下划线的函数一般是函数库内部的函数,而不带下划线的一般是提供给用户使用的函数。这是为了防止用户定义的函数和函数库的函数重名冲突。这个经验使我更加熟悉了Visual Studio 2022开发平台的使用,并对函数库的命名规范有了更清晰的认识。
📝总结
图形学领域宛如一片广阔而未被完全探索的创意海洋,邀请你勇敢踏足数字艺术和计算机图形学的神秘领域。这是一场富有创意和技术挑战的学习之旅,从基础概念到算法实现,逐步揭示更深层次的图形分析、渲染技术和智能图形识别的奥秘。渴望挑战图形学的学习路径和掌握计算机艺术的技能?不妨点击下方链接,一同探讨更多数字创意的奇迹吧。我们推出了引领趋势的💻 计算机图形学专栏:《艺术之光 | 数字创新解锁》,旨在深度探索图形学技术的实际应用和创新。🌐🎨

相关文章:

【图形学】探秘图形学奥秘:DDA与Bresenham算法的解密与实战
🌈个人主页:Sarapines Programmer🔥 系列专栏:《图形学 | 图像解码》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 🌌1. 初识模式识别…...
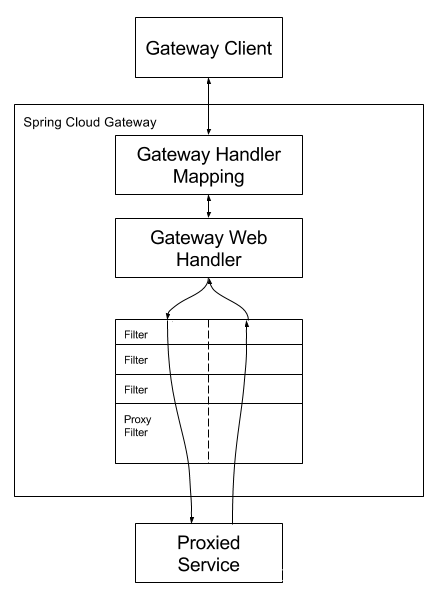
微服务-Gateway
案例搭建 官网地址 父Pom <com.alibaba.cloud.version>2.2.8.RELEASE</com.alibaba.cloud.version> <com.cloud.version>Hoxton.SR12</com.cloud.version> <com.dubbo.version>2.2.7.RELEASE</com.dubbo.version> <dependencyManagem…...

【用队列实现栈】【用栈实现队列】Leetcode 232 225
【用队列实现栈】【用栈实现队列】Leetcode 232 225 队列的相关操作栈的相关操作用队列实现栈用栈实现队列 ---------------🎈🎈题目链接 用队列实现栈🎈🎈------------------- ---------------🎈🎈题目链…...

Angular系列教程之观察者模式和RxJS
文章目录 引言RxJS简介RxJS中的设计模式观察者模式迭代器模式 示例代码RxJS 在 Angular 中的应用总结 引言 在Angular开发中,我们经常需要处理异步操作,例如从后端获取数据或与用户的交互。为了更好地管理这些异步操作,Angular中引入了RxJS&…...

展厅设计中搭建的小常识
1、展厅的安全问题 展厅的空间面积大,平时为出现公开展览时人员较少,但遇到开展活动、会展展览时人流量将大大增多,无论是临时的展厅展示还是长期的展示安全问题即使不说都应该是装饰的重中之重,所以在从前期设计规划到后期施工采…...

LeetCode 98. 验证二叉搜索树
98. 验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 示例…...
)
自定义shell工具函数之pull_image()
这是一个名为pull_image的Shell脚本函数。让我来解释一下这个函数的功能: function pull_image() {image$1DOCKER_IMAGE_MIRROR$(get_config_or_env DOCKER_IMAGE_MIRROR)if [[ "${DOCKER_IMAGE_MIRROR}" "1" ]]; thenif [[ "$(uname -m…...

2019年认证杯SPSSPRO杯数学建模C题(第二阶段)保险业的数字化变革全过程文档及程序
2019年认证杯SPSSPRO杯数学建模 基于统计建模的车险业数字变革研究 C题 保险业的数字化变革 原题再现: 车险,即机动车辆保险。保险自身是一种分散风险、消化损失的经济补偿制度,车险即为分散机动车辆在行驶过程中可能发作的未知风险和损失…...
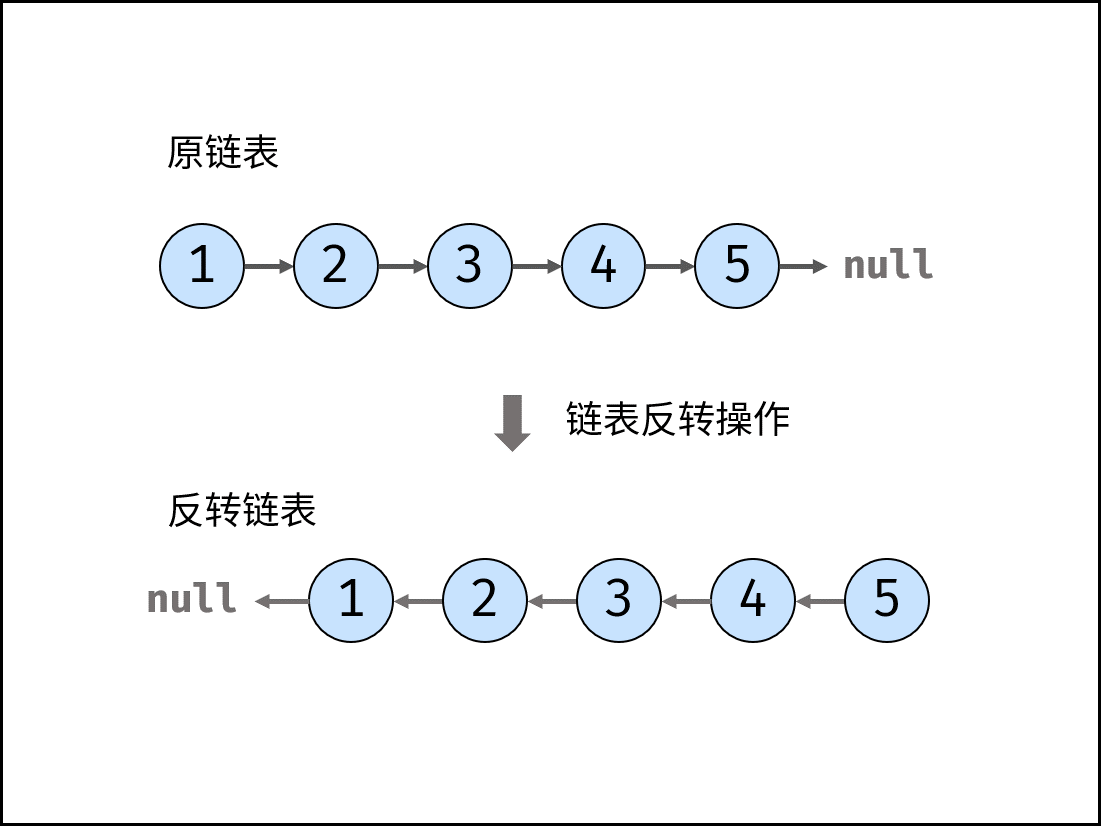
【数据结构和算法】反转链表
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 方法一:迭代(双指针) 2.2 方法二:递归 三、代码 3.…...

What is `GenericFilterBean` does?
GenericFilterBean 是 SpringWeb 框架中提供的一个抽象基类,其对 javax.servlet.Filter接口进行了封装和扩展,它简化了在 Servlet环境下创建自定义过滤器的工作。 GenericFilterBean 主要特点包括: 集成 Spring 容器: 由于它是一…...

突破通胀风险,聚焦现货黄金投资机遇
随着全球经济不断发展和金融市场的波动,通胀风险成为各界关注的焦点。在面对通胀带来的财务压力和资产贬值的威胁时,投资者都在寻找稳定且可靠的避险资产。而现货黄金作为一种值得瞩目的投资工具,正吸引着越来越多投资者的目光。 黄金作为一种…...
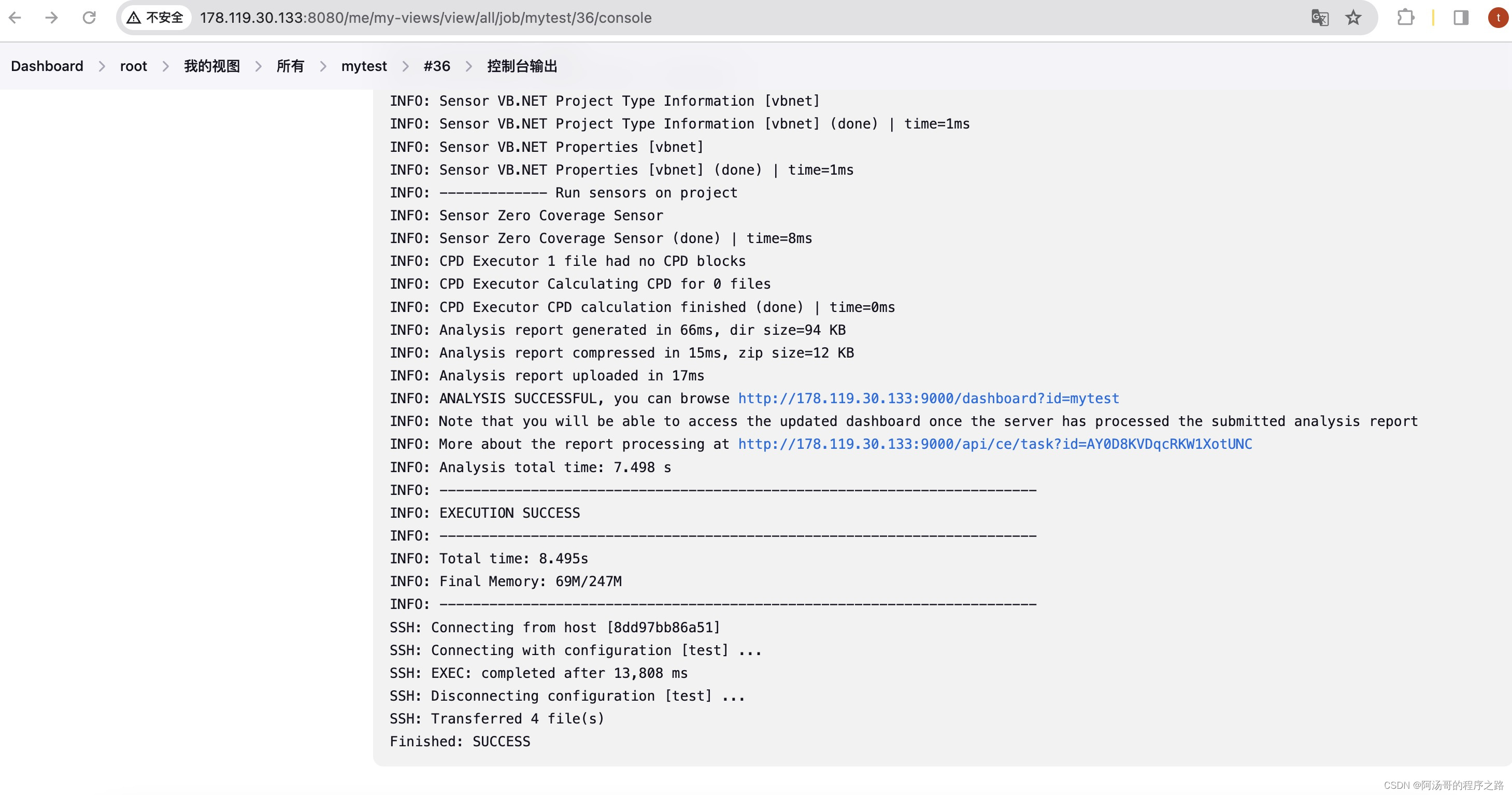
Jenkins集成Sonar Qube
下载插件 重启Jenkins 容器 sonarqube 使用令牌 Jenkins 配置 重新构建...
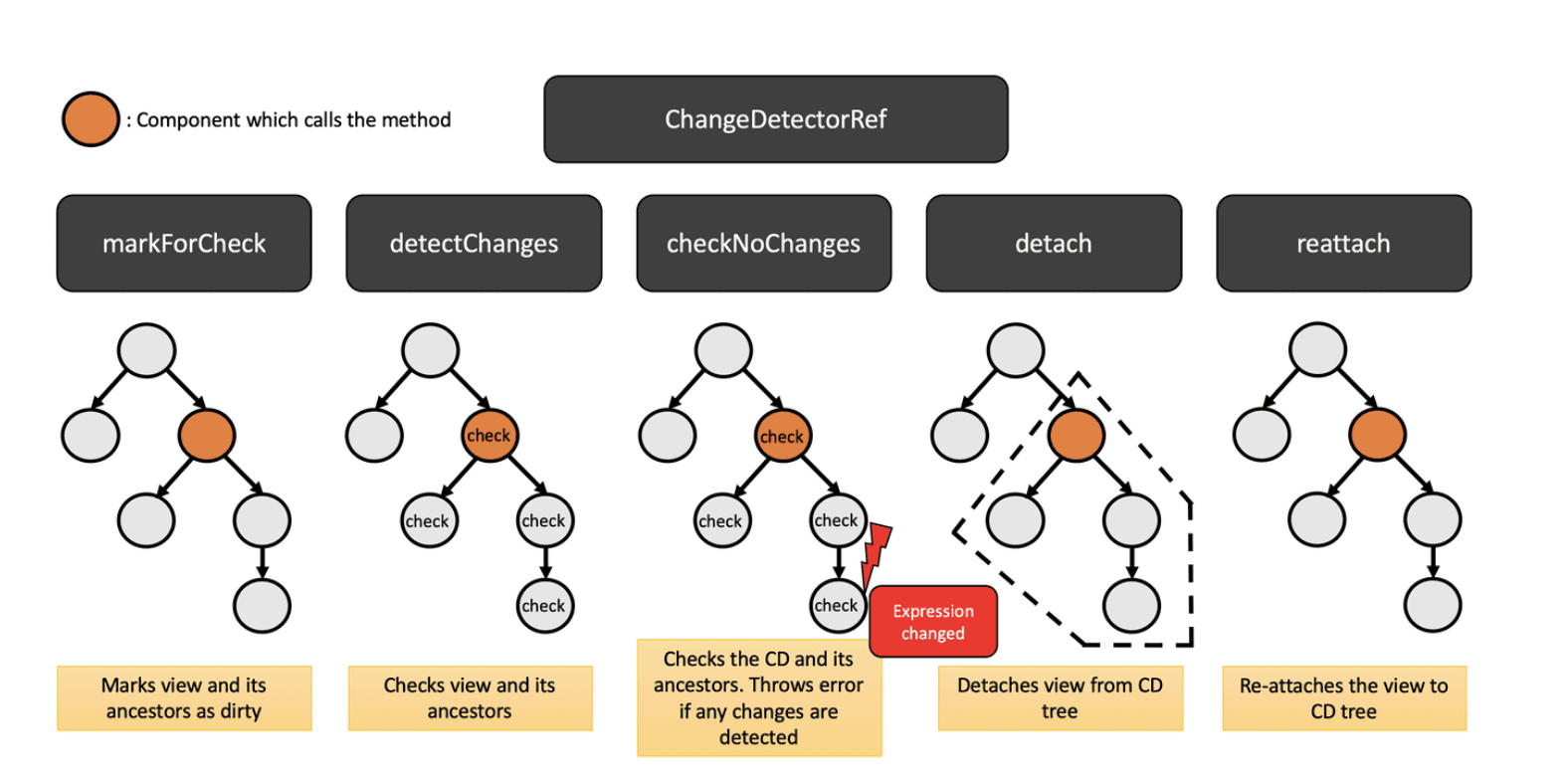
Angular系列教程之zone.js和NgZone
文章目录 什么是zone.jsZone的工作原理Zone的常见用途NgZone:Angular中的zone.js使用NgZone使用NgZone执行代码使用NgZone外部检测 结论 什么是zone.js 在Angular中,zone.js是一个非常重要的库,它为我们提供了一种跟踪和管理异步操作的机制。…...
阿里巴巴的第二代通义千问可能即将发布:Qwen2相关信息已经提交HuggingFace官方的transformers库
本文来自DataLearnerAI官方网站:阿里巴巴的第二代通义千问可能即将发布:Qwen2相关信息已经提交HuggingFace官方的transformers库 | 数据学习者官方网站(Datalearner) 通义千问是阿里巴巴开源的一系列大语言模型。Qwen系列大模型最高参数量720亿…...
编程的练习:查找字符)
肯尼斯·里科《C和指针》第6章 指针(6)编程的练习:查找字符
1.编写一个函数,它在一个字符串中进行搜索,查找在一个给定字符集合中出现的所有字符。这个函数的原型如下: char *find_char( char const *source, char const *chars ); 它的基本想法是查找source字符串中匹配chars字符串中任何字符的第1个…...

Entity Framework知识点整理
Entity Framework Entity Framework(EF)是微软提供的一种对象关系映射(Object-Relational Mapping,ORM)框架,用于在.NET应用程序和关系型数据库之间建立映射关系。它简化了数据访问层的开发,使…...

源码搭建教学:连锁餐饮APP开发实战
连锁餐饮APP,对于很多从事餐饮行业的人来说不会陌生,同样这个项目本身就有着很高的热度。今天,小编将深入为大家讲述一下此系统的前后端开发、数据库设计、用户界面设计等方面,让您深入了解全栈开发的方方面面。 一、项目准备与规…...

使用JavaScript实现一个在线画板
一、引言 随着Web技术的发展,网页上的交互性变得越来越重要。一个在线画板是一个很好的例子,它允许用户在网页上自由创作。在这篇博客中,我们将使用HTML5的Canvas元素和JavaScript来实现一个简单的在线画板 二、HTML结构 首先,…...

微信小程序如何自定义导航栏,怎么确定导航栏及状态栏的高度?导航栏被刘海、信号图标给覆盖了怎么办?
声明:本文为了演示效果,颜色采用的比较显眼,可根据实际情况修改颜色 问题描述 当我们在JSON中将navigationStyle设置成custom后,当前页面的顶部导航栏就需要我们制作了,但出现了一下几个问题: 导航栏的高…...

Spring Boot “How-to“ 指南中文文档-上
本文为官方文档直译版本。原文链接 篇幅较长,遂分两篇 Spring Boot "How-to" 指南中文文档-上 引言Spring Boot Application创建自己的FailureAnalyzer(故障分析器)自动配置故障诊断启动前自定义环境或应用程序上下文构建 Applicat…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
