go语言(二)----常量
1、单个常量用const进行定义。 const a int = 100
2、多个常量用const()进行定义。
const (
a = 10
b = 20 )
3、iota 与const()来表示枚举类型
const(
a = iota
b
c
)
package mainimport "fmt"const (//可以在const()添加一个关键字iota,每行的iota都会累加1,第一行的iota的默认值是0//iota只能在const中,配合const()一起使用BEIJING = 10 * iota //iota = 0SHANGHAI //iota =1shenzhen //iota = 2
)func main() {const name int = 10fmt.Println("name = ",name)fmt.Println("BEIJING = ",BEIJING)fmt.Println("SHANGHAI = ",SHANGHAI)fmt.Println("SHENZHEN = ",shenzhen)
}
相关文章:

go语言(二)----常量
1、单个常量用const进行定义。 const a int 100 2、多个常量用const()进行定义。 const ( a 10 b 20 ) 3、iota 与const()来表示枚举类型 const( a iota b c ) package mainimp…...

VSC ctrl+鼠标左键点击后,返回原来位置的方法
windows 在使用VSC编写代码时,我们常常用到Ctrl鼠标左键的方式来查看类或变量名的定义声明,看完之后我们想回到程序原来的位置,此时可以通过Alt ←(方向左键)来返回到原来的位置。...
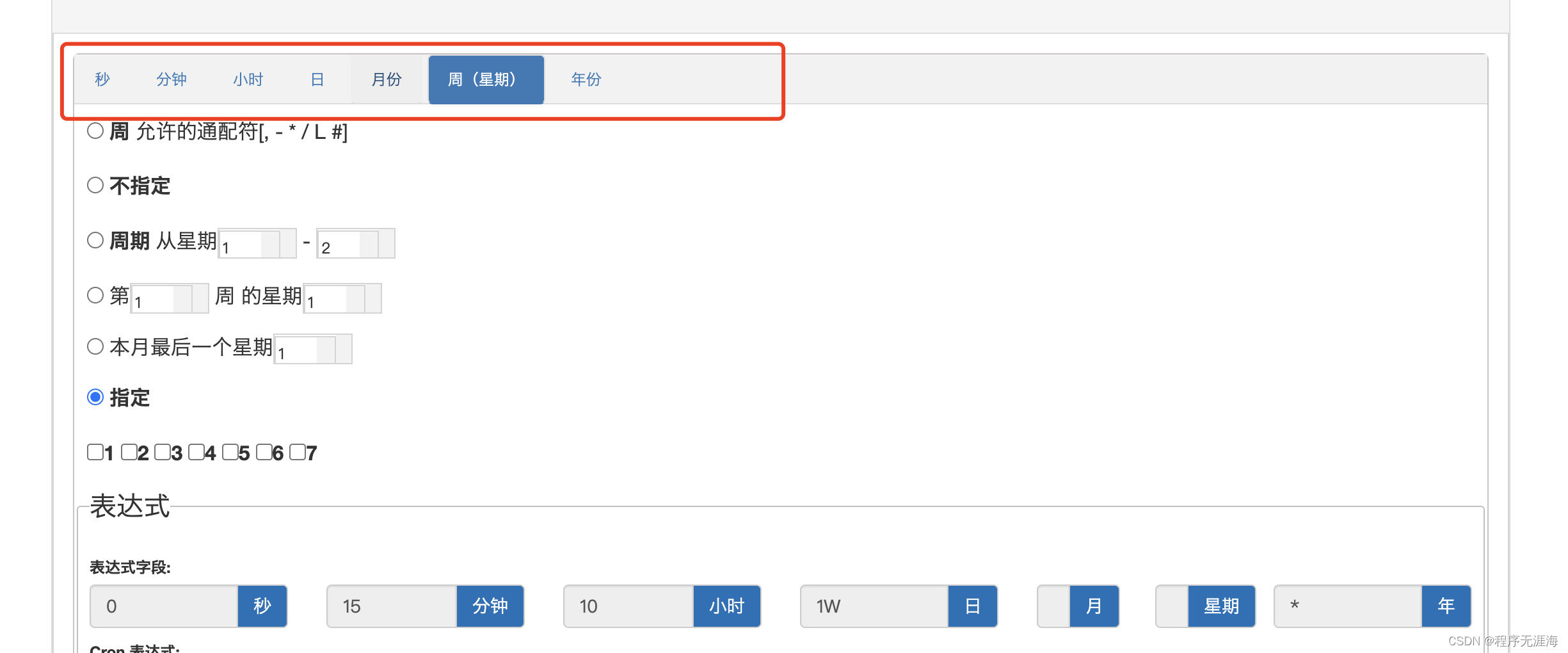
还在为crontab表达式发愁吗,快使用这个工具
是不是每次要定义cron表达式的时候,都去百度翻找资料,cron表达式难写难记真是苦天下程序员久已。有没有什么不拥记的办法就轻松掌握呢?最近发现这个CrontabGuru神器,强烈推荐,真是广大程序员的福音了。 简介 Crontab…...

61. Spring事务传播行为实现原理
61. Spring事务传播行为实现原理 Spring的事务信息是存在ThreadLocal中的, 所以一个线程永远只能有一个事务 融入:当传播行为是融入外部事务则拿到ThreadLocal中的Connection、共享一个数据库连接共同提交、回滚;创建新事务:当传播行为是创建新事务,会将嵌套新事务存入Th…...
智能合约笔记
前言: 首先了解下为什么会出现智能合约,打个比方现在有两个人A和B打赌明天会不会下雨,每个人赌注100元,如果第二天下雨则A拿走200元,否则B拿走200元,这样就有一个问题,赌注要到第二天才能见效&…...
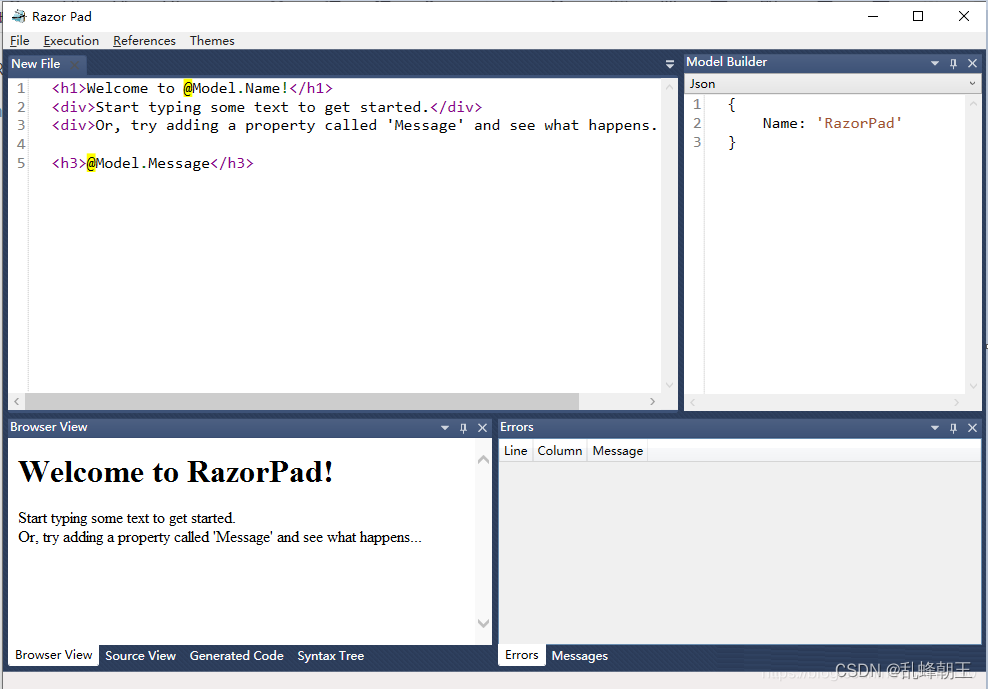
脱离于ASP.NET 和Visual Studio编辑Razor脚本
Razor Pad是一个编辑Razor脚本的工具,脱离于ASP.NET 和Visual Studio。 github地址:GitHub - RazorPad/RazorPad: RazorPad is a quick and simple stand-alone editing environment that allows anyone (even non-developers) to author Razor templat…...
MetaGPT前期准备与快速上手
大家好,MetaGPT 是基于大型语言模型(LLMs)的多智能体协作框架,GitHub star数量已经达到31.3k。 接下来我们聊一下快速上手 这里写目录标题 一、环境搭建1.python 环境2. MetaGpt 下载 二、MetaGPT配置1.调用 ChatGPT API 服务2.简…...
Java、C#、Python间的Battle
一、编译原理和开发效率 编译速度: C# (约大于等于) JAVA > Python python的编译原理 前提:python 3.6 python不会直接编译源码 而是把源码直接扔给解释器,这种方式 使得python非常灵活,让它的开发效…...

【图形学】探秘图形学奥秘:DDA与Bresenham算法的解密与实战
🌈个人主页:Sarapines Programmer🔥 系列专栏:《图形学 | 图像解码》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 🌌1. 初识模式识别…...
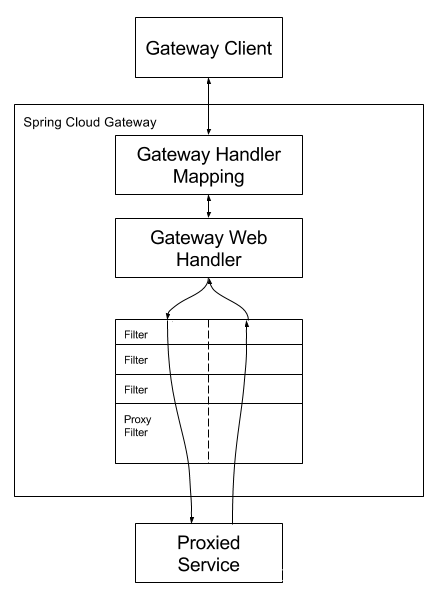
微服务-Gateway
案例搭建 官网地址 父Pom <com.alibaba.cloud.version>2.2.8.RELEASE</com.alibaba.cloud.version> <com.cloud.version>Hoxton.SR12</com.cloud.version> <com.dubbo.version>2.2.7.RELEASE</com.dubbo.version> <dependencyManagem…...

【用队列实现栈】【用栈实现队列】Leetcode 232 225
【用队列实现栈】【用栈实现队列】Leetcode 232 225 队列的相关操作栈的相关操作用队列实现栈用栈实现队列 ---------------🎈🎈题目链接 用队列实现栈🎈🎈------------------- ---------------🎈🎈题目链…...

Angular系列教程之观察者模式和RxJS
文章目录 引言RxJS简介RxJS中的设计模式观察者模式迭代器模式 示例代码RxJS 在 Angular 中的应用总结 引言 在Angular开发中,我们经常需要处理异步操作,例如从后端获取数据或与用户的交互。为了更好地管理这些异步操作,Angular中引入了RxJS&…...

展厅设计中搭建的小常识
1、展厅的安全问题 展厅的空间面积大,平时为出现公开展览时人员较少,但遇到开展活动、会展展览时人流量将大大增多,无论是临时的展厅展示还是长期的展示安全问题即使不说都应该是装饰的重中之重,所以在从前期设计规划到后期施工采…...

LeetCode 98. 验证二叉搜索树
98. 验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 示例…...
)
自定义shell工具函数之pull_image()
这是一个名为pull_image的Shell脚本函数。让我来解释一下这个函数的功能: function pull_image() {image$1DOCKER_IMAGE_MIRROR$(get_config_or_env DOCKER_IMAGE_MIRROR)if [[ "${DOCKER_IMAGE_MIRROR}" "1" ]]; thenif [[ "$(uname -m…...

2019年认证杯SPSSPRO杯数学建模C题(第二阶段)保险业的数字化变革全过程文档及程序
2019年认证杯SPSSPRO杯数学建模 基于统计建模的车险业数字变革研究 C题 保险业的数字化变革 原题再现: 车险,即机动车辆保险。保险自身是一种分散风险、消化损失的经济补偿制度,车险即为分散机动车辆在行驶过程中可能发作的未知风险和损失…...
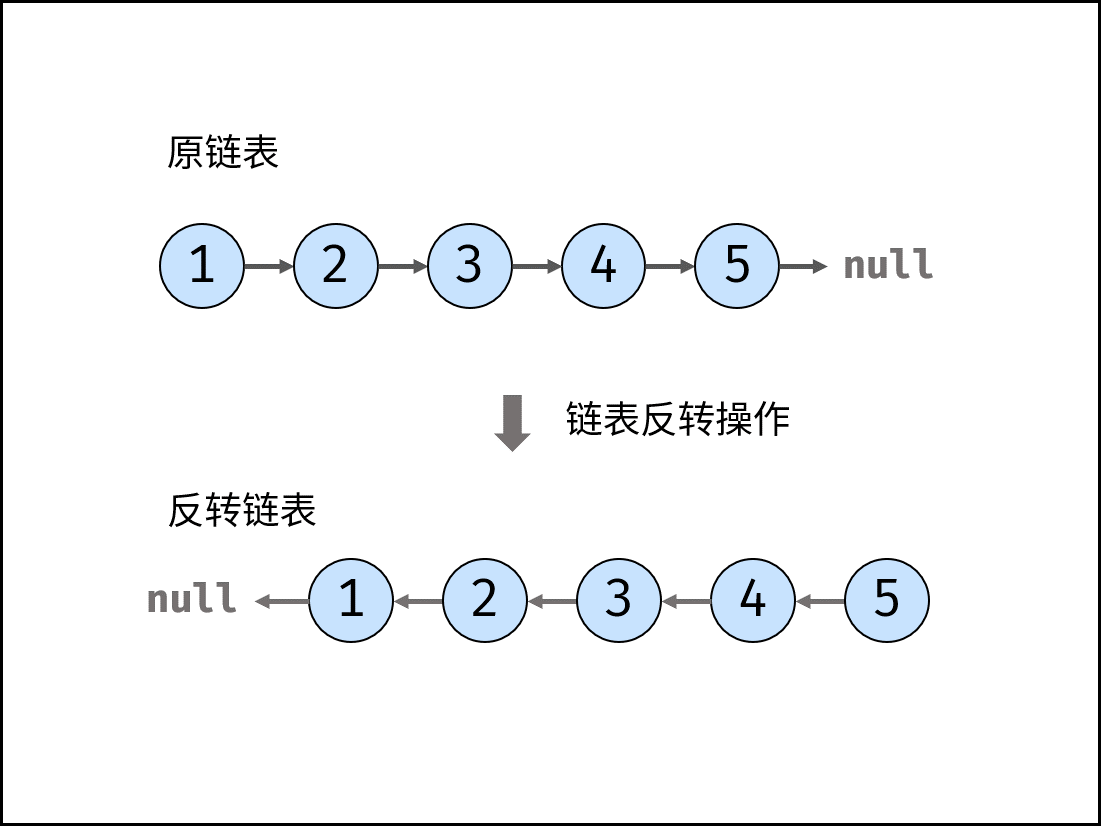
【数据结构和算法】反转链表
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 方法一:迭代(双指针) 2.2 方法二:递归 三、代码 3.…...

What is `GenericFilterBean` does?
GenericFilterBean 是 SpringWeb 框架中提供的一个抽象基类,其对 javax.servlet.Filter接口进行了封装和扩展,它简化了在 Servlet环境下创建自定义过滤器的工作。 GenericFilterBean 主要特点包括: 集成 Spring 容器: 由于它是一…...

突破通胀风险,聚焦现货黄金投资机遇
随着全球经济不断发展和金融市场的波动,通胀风险成为各界关注的焦点。在面对通胀带来的财务压力和资产贬值的威胁时,投资者都在寻找稳定且可靠的避险资产。而现货黄金作为一种值得瞩目的投资工具,正吸引着越来越多投资者的目光。 黄金作为一种…...
Jenkins集成Sonar Qube
下载插件 重启Jenkins 容器 sonarqube 使用令牌 Jenkins 配置 重新构建...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
