机器学习算法 - 马尔可夫链
马尔可夫链(Markov Chain)可以说是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测、语音识别方面都有着极其广泛的应用
> The future is independent of the past given the present 未来独立于过去,只基于当下。
这句人生哲理的话也代表了马尔科夫链的思想:过去所有的信息都已经被保存到了现在的状态,基于现在就可以预测未来。
虽然这么说可能有些极端,但是却可以大大简化模型的复杂度,因此马尔可夫链在很多时间序列模型中得到广泛的应用,比如循环神经网络 RNN,隐式马尔可夫模型 HMM 等,当然 MCMC 也需要它。
随机过程
马尔可夫链是随机过程 这门课程中的一部分,先来简单了解一下。
简单来说,随机过程就是使用统计模型一些事物的过程进行预测和处理 ,比如股价预测通过今天股票的涨跌,却预测明天后天股票的涨跌;天气预报通过今天是否下雨,预测明天后天是否下雨。这些过程都是可以通过数学公式进行量化计算的。通过下雨、股票涨跌的概率,用公式就可以推导出来 N 天后的状况。
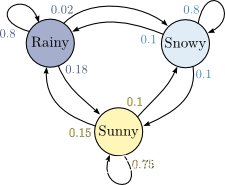
简介
俄国数学家 Andrey Andreyevich Markov 研究并提出一个用数学方法就能解释自然变化的一般规律模型,被命名为马尔科夫链(Markov Chain)。马尔科夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程,该过程要求具备“无记忆性 ”,即下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。
马尔科夫链认为过去所有的信息都被保存在了现在的状态下了 。比如这样一串数列 1 - 2 - 3 - 4 - 5 - 6,在马尔科夫链看来,6 的状态只与 5 有关,与前面的其它过程无关。
数学定义
假设我们的序列状态是,那么在
时刻的状态的条件概率仅依赖于前一刻的状态
即:
既然某一时刻状态转移的概率只依赖于它的前一个状态 ,那么我们只要能求出系统中任意两个状态之间的转换概率,这个马尔科夫链的模型就定了。
转移概率矩阵
通过马尔科夫链的模型转换,我们可以将事件的状态转换成概率矩阵 (又称状态分布矩阵 ),如下例:
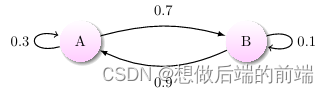
上图中有 A 和 B 两个状态,A 到 A 的概率是 0.3,A 到 B 的概率是 0.7;B 到 B 的概率是 0.1,B 到 A 的概率是 0.9。
初始状态在 A,如果我们求 2 次运动后状态还在 A 的概率是多少?非常简单: P=A→A→A+A→B→A=0.3∗0.3+0.7∗0.9=0.72
如果求 2 次运动后的状态概率分别是多少?初始状态和终止状态未知时怎么办呢?这是就要引入转移概率矩阵 ,可以非常直观的描述所有的概率。
有了状态矩阵,我们可以轻松得出以下结论:
- 初始状态 A,2 次运动后状态为 A 的概率是 0.72;
- 初始状态 A,2 次运动后状态为 B 的概率是 0.28;
- 初始状态 B,2 次运动后状态为 A 的概率是 0.36;
- 初始状态 B,2 次运动后状态为 B 的概率是 0.64;
来看一个多个状态更复杂的情况:

状态转移矩阵的稳定性
状态转移矩阵有一个非常重要的特性,经过一定有限次数序列的转换,最终一定可以得到一个稳定的概率分布 ,且与初始状态概率分布无关。例如
假设我们当前股市的概率分布为: [ 0.3 , 0.4 , 0.3 ] [0.3, 0.4, 0.3][0.3,0.4,0.3] ,即 30% 概率的牛市,40% 概率的熊盘与 30% 的横盘。然后这个状态作为序列概率分布的初始状态,将其代入这个状态转移矩阵计算
的状态。代码如下:
matrix = np.matrix([[0.9, 0.075, 0.025],[0.15, 0.8, 0.05],[0.25, 0.25, 0.5]], dtype=float)
vector1 = np.matrix([[0.3, 0.4, 0.3]], dtype=float)for i in range(100):vector1 = vector1 * matrixprint('Courrent round: {}'.format(i+1))print(vector1)
输出结果:
Current round: 1
[[ 0.405 0.4175 0.1775]]
Current round: 2
[[ 0.4715 0.40875 0.11975]]
Current round: 3
[[ 0.5156 0.3923 0.0921]]
Current round: 4
[[ 0.54591 0.375535 0.078555]]
。。。。。。
Current round: 58
[[ 0.62499999 0.31250001 0.0625 ]]
Current round: 59
[[ 0.62499999 0.3125 0.0625 ]]
Current round: 60
[[ 0.625 0.3125 0.0625]]
。。。。。。
Current round: 99
[[ 0.625 0.3125 0.0625]]
Current round: 100
[[ 0.625 0.3125 0.0625]]
可以发现,从第 60 轮开始,我们的状态概率分布就不变了,一直保持[ 0.625 , 0.3125 , 0.0625 ],即 62.5% 的牛市,31.25% 的熊市与 6.25% 的横盘。
这个性质不仅对状态转移矩阵有效,对于绝大多数的其他的马尔可夫链模型的状态转移矩阵也有效。同时不光是离散状态,连续状态时也成立。
马尔科夫链的应用
语言模型
自然语言处理、语音处理中经常用到语言模型, 是建立在词表上的 n nn 阶马尔可夫链。比如, 在英语语音识别中,语音模型产生出两个候选: “How to recognize speech” 与 "How to wreck a nice beach”,语言模型要判断哪个可能性更大
将一个语句看作是一个单词的序列 ,目标是计算其概率。同一个语句很少在语料中重复多次出现,所以直接从语料中估计每个语句的概率是困难的。语言模型用局部的单词序列的概率,组合计算出全局的单词序列的概率,可以很好地解决这个问题。假设每个单词只依赖于其前面出现的单词,也就是说单词序列具有马尔可夫性,那么可以定义一阶马尔可夫链 (可以轻易扩展到 n 阶马尔可夫链),即语言模型,如下计算语句的概率:
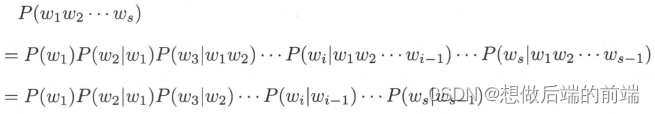
如果有充分的语料,转移概率可以直接从语料中估计。直观上, “wreck a nice” 出现之后,下面出现 “beach” 的概率极低,所以第二个语句的概率应该更小,从语言模型的角度看第一个语句的可能性更大
信号传输
考虑通过电话线或无线电波传输信号的问题。每条数据都必须经过一个多阶段的过程才能传输,并且在每个阶段都存在传输错误导致数据损坏的概率。
假设传输中发生错误的概率不受过去传输错误的影响,不依赖于时间,并且可能的数据条数是有限的。然后可以通过马尔可夫链建模传输过程,状态为0和1以及转移矩阵

相关文章:

机器学习算法 - 马尔可夫链
马尔可夫链(Markov Chain)可以说是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测、语音识别方面都有着极其广泛的应用 > The future is independent of the past given the present 未来独立于过去ÿ…...

Linux下防火墙相关命令整理
目录 一.前言二.相关命令整理 一.前言 这篇文章简单整理一下Linux系统中防火墙相关命令。 二.相关命令整理 开启防火墙 systemctl start firewalld关闭防火墙 systemctl stop firewalld重启防火墙 systemctl restart firewalld开机启用防火墙 systemctl enable firewall…...

Python八股文总结
一. Python基本数据结构有哪四种?区别是什么? 列表(List)元组(Tuple)字典(Dictionary)集合(Set) 区别主要在于它们的可变性(是否可以修改&#x…...
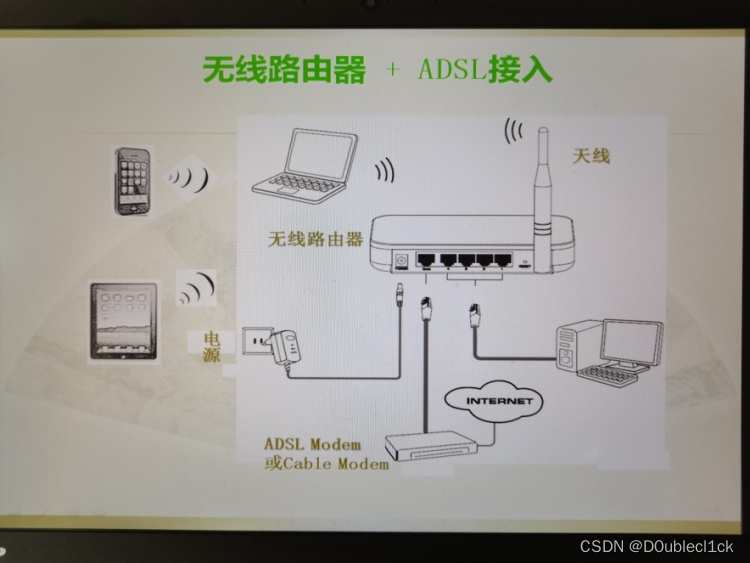
计算机导论05-计算机网络
文章目录 计算机网络基础计算机网络概述计算机网络的概念计算机网络的功能计算机网络的组成 计算机网络的发展计算机网络的类型 网络体系结构网络互联模型OSI/RM结构与功能TCP/IP结构模型TCP/IP与OSI/RM的比较 网络地址与分配IP地址构成子网的划分IPv6 传输介质与网络设备网络传…...

sentinel熔断与限流
文章目录 一、sentinel简介Sentinel 是什么?Sentinel安装 二、sentinel整合工程新建cloudalibaba-sentinel-service8401微服务引入依赖yml配置主启动类添加EnableDiscoveryClient业务类测试 三、sentinel流控规则基本介绍流控模式直接(默认)关…...
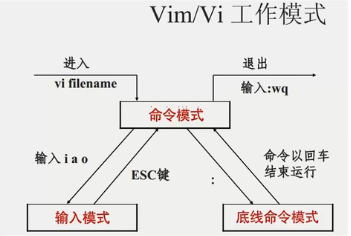
vi/vim 编辑器 --基本命令
1 vi/vim编辑器介绍 vi 是visual interface 的简称,是Linux中最经典的文本编辑器 vim是vi的加强版。兼容了vi的所有指令,不仅能编辑文本,而且具有shell程序编辑的功能,可以通过不同颜色的字体辨别语法的正确性,极大…...

C++——STL标准模板库——容器详解——set
一、基本概念 set容器是一种具备自动排序功能的集合,默认递增排序;元素无法直接修改,且不能重复;另一个版本叫做multiset,允许存在重复元素,其他功能和性质一样。 set容器底层结构一般为自平衡二叉搜索树…...
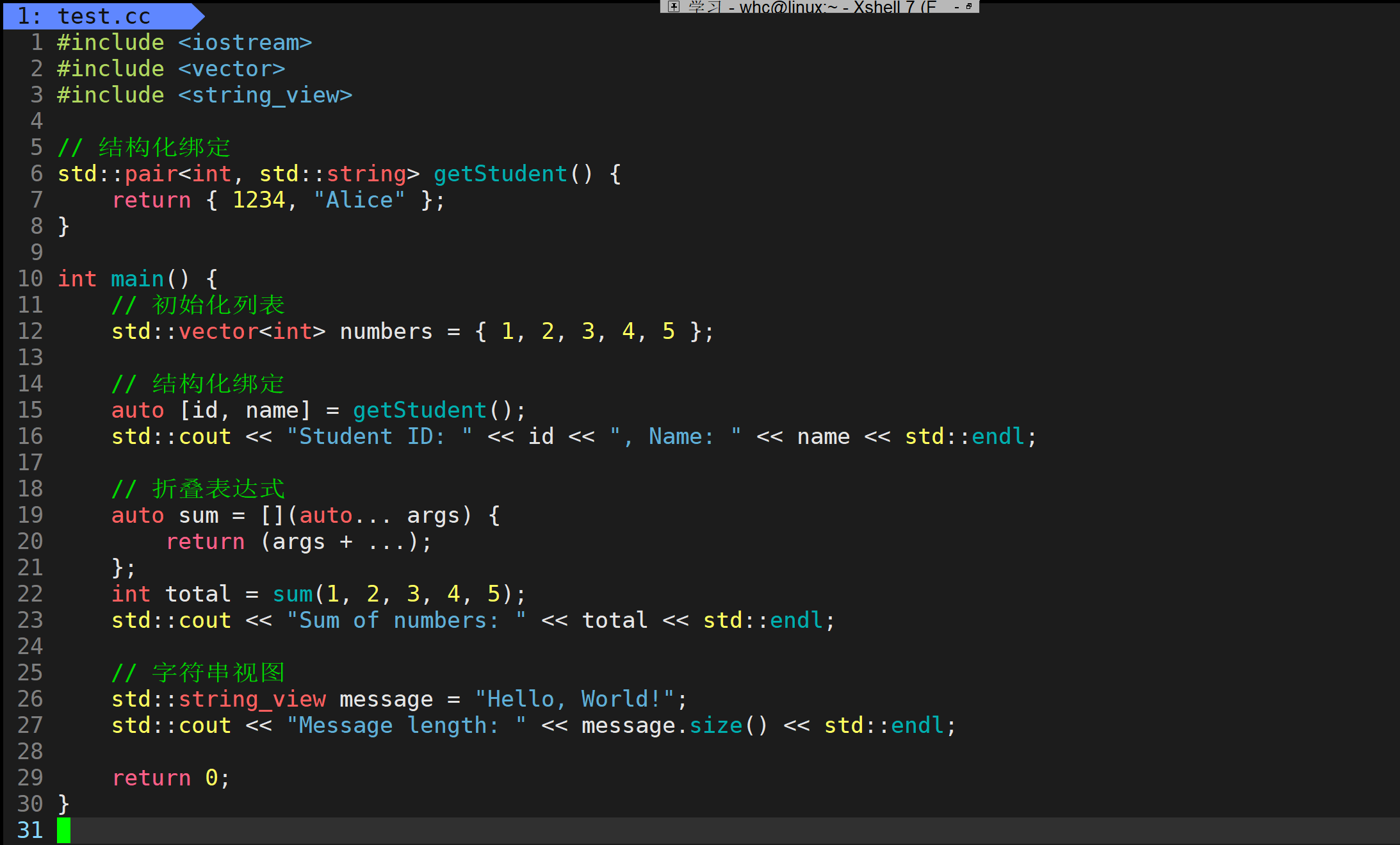
Vim一键配置指南,打造高效率C++开发环境
文章目录 前言安装与卸载功能演示gcc/g升级问题 前言 Vim作为当下最受欢迎的文本编译器之一,不仅具有强大的文本编辑功能,还提供了高度的可定制性。用户可以根据自己的喜好自定义配置,并且通过自己编写插件或者使用现有的插件来扩展Vim的功能…...

新航向,新生态: Michael在出海业务圆桌会议分享HyperBDR全球业务拓展之道
1月15日-16日,以“领航新开局,共赢新生态”为主题的华为云生态大会2024在华为云贵安数据中心云上屯盛大举行。本次会议聚焦于华为云全国生态伙伴与开发者,旨在共同见证华为云生态战略的最新进展和伙伴政策的新升级。与会者将分享来自优秀生态…...

SpringBoot异步处理
Spring boot异步处理 业务场景: 如执行数据库备份任务,前端发起请求到后端,后端备份数据库的处理逻辑需要很长一段时间,此时前端会一直等待后端返回结果,给用户给等待时间过长,这是就要考虑异步处理了&…...
2024年甘肃省职业院校技能大赛信息安全管理与评估 样题一 模块二
竞赛需要完成三个阶段的任务,分别完成三个模块,总分共计 1000分。三个模块内容和分值分别是: 1.第一阶段:模块一 网络平台搭建与设备安全防护(180 分钟,300 分)。 2.第二阶段:模块二…...

matplotlib绘制动态瀑布图
绘制瀑布图思路:遍历指定文件目录下所有的csv文件,每读一个文件,取文件前20行数据进行保存,如果超过规定的行数300行,将最旧的数据删除,仅保留300行数据进行展示。 网上找的大部分绘制瀑布图的代码&#x…...

【STM32】STM32学习笔记-USART串口收发HEX和文本数据包(29)
00. 目录 文章目录 00. 目录01. 串口简介02. 串口收发HEX数据包接线图03. 串口收发HEX数据包示例104. 串口收发HEX数据包示例205. 串口收发文本数据包接线图06. 串口收发文本数据包示例07. 程序示例下载08. 附录 01. 串口简介 串口通讯(Serial Communication)是一种设备间非常…...

uniapp列表实现方式 v-for
创建列表视图 v-for v-for“对象item in 数组” v-for“(对象item,下标) in 数组” v-for“(对象item,使用这个键取到的值,下标) in 数组” :key 绑定标识 一般建议使用对象中的id等值 类型 any <template><view><view clas…...

SqlAlchemy使用教程(三) CoreAPI访问与操作数据库详解
SqlAlchemy使用教程(一) 原理与环境搭建SqlAlchemy使用教程(二) 入门示例及编程步骤 三、使用Core API访问与操作数据库 Sqlalchemy 的Core部分集成了DB API, 事务管理,schema描述等功能,ORM构筑于其上。本章介绍创建 Engine对象,使用基本的…...
PDF有编辑密码怎么办
目录 注意: windows方法: 1 python 下载 2 打开命令行 3 安装 pikepdf 4 编写python脚本 5 使用py脚本 6解密完成 Linux方法: 注意: 此方法可以用于破解PDF的编辑密码,而不是PDF的打开密码 当遇到类似如下问…...

智慧公厕:打造智慧城市公共厕所信息化管理的新升级
在现代社会中,随着科学技术的不断进步与应用,智慧公厕作为公共服务设施,正迎来一次新的升级与革新。利用先进技术,智慧公厕实现了信息化升级,能够实时监测人员、环境和设备状况,提高使用效率、安全性、舒适…...

gin-vue-admin二开使用雪花算法生成唯一标识 id
场景介绍 需求场景: 总部采集分支的数据,由于分支的 id 是子增的主键 id,所以会出现重复的 id,但是这个 id 需要作为标识,没有实际作用,这里选择的是分布式 id 雪花算法生成 id 存储用来标识,这…...
文心一言 vs. ChatGPT:哪个更胜一筹?
文心一言 vs. ChatGPT:从简洁美到深度思考的文本生成之旅 近年来,文本生成工具的崛起使得人们在表达和沟通方面拥有了更多的选择。在这个领域中,文心一言和ChatGPT作为两个备受瞩目的工具,各自以独特的优势展现在用户面前。本文将…...

LoadBalancer 替换 Ribbon
POM 移除 Ribbon 相关依赖 <!-- LoadBalancer 必须引入 springcloud --> <!-- 父pom引入springcloud 版本管理 --> https://spring.io/projects/spring-cloud/ 官网查看 boot 对应的 cloud 的版本 <dependencyManagement><dependency> <groupI…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
