基于 Level set 方法的医学图像分割
摘 要
医学图像分割是计算机辅助诊断系统设计中的关键技术。对于医学图像分割问题,它一般可分为两部分:(l)图像中特定目标区域(器官或组织)的识别;(2)目标区域完整性的描述与提取。相比于其他图像,医学图像的复杂性和多样性,使得传统的基于底层图像信息的分割方法很难取得好的分割结果,而结合了高层视觉先验知识和图像底层信息的主动轮廓模型,符合人类视觉认知事物的一般规律,在计算机辅助诊断中得到了广泛的应用。水平集方法的出现,极大推动了主动轮廓模型的发展。水平集方法和曲线演化模型相结合,克服了传统Snakes模型的很多固有缺陷,大大拓展了主动轮廓模型的应用领域。本文系统的介绍了水平集方法在医学图像分割的应用与发展。
关键词: 医学图像分割 水平集方法 主动轮廓模型

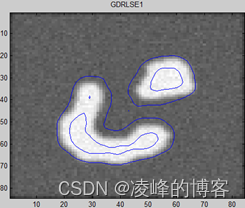

一、概述
水平集方法在图像分割中的应用源于活动轮廓模型。活动轮廓模型方法,是基于局部梯度的一种边界方法。通过对能量函数进行最小化,获得需要的边界,它更多的被用来跟踪变形的运动物体。但是,主动轮廓模型对噪声敏感,更主要的是它得到的结果常依赖于初始化,并且不具有足够拓扑适应性。所以人们又引进了 Balloon 模型,这里对施加到曲线上的外力进行了修改,以减少主动轮廓对弱边缘的敏感性。在基于区域的方法中,有种子区域生长和分裂合并法。利用马尔可夫随机场模型形成的全局标注问题,并对能量函数进行最小化来求解。人们还尝试把轮廓和基于区域的方法结合起来获得新的方法。Zhu S 和 Yuille A[1]介绍了一种区域竞争的方法,把 Snakes/Balloon 的几何特点和区域生长的理论结合起来,取得了一定的效果。自从 Malladi, Sethian 等人[2]把 Level set 法[3]引进到曲线进化中来以后,事实证明 Level set 法在解决曲线进化方程问题时是一个相当有力的工具。Level set 法的优点是:可以处理尖锐的角落,并具有很强的改变拓扑的能力。它可以把具有相当复杂的物体边界分割出来,这是活动轮廓等方法所难以达到的,特别是在处理具有复杂外形的医学图像时,优点更明显。随着近几年医学与信息技术的发展,国内外学者们对水平集方法有了许多的改进,取得了很多令人满意的结果,且在某些器官或组织的分割上,已经达到了临床的要求,甚至比专业医生手工分割的结果还要准确。Q.J.xie[4]等提出一种改进的水平集方法对腹部MRI的肝脏进行分割.孟令旗[5]等提出高斯分布和瑞利分布相结合的方法进行概率密度函数的确定与分析,通过随机极大似然算法SEM把瑞利分布引入到水平集三维分割演化模型中,成功的分割了三维肺CT图像。
二、曲线演化
水平集方法(Level set Method)是在研究曲线演化时提出来的,用于描述曲线的演化过程,它以隐含的方式表达平面闭合曲线,将曲线演化转化为求解偏微分方程的数值问题。
曲线演化理论是研究曲线变化的数学理论。曲线演化理论的目的是仅使用几何度量研究曲线变形,这些几何度量包括单位法向量,曲率。而在参数变形模型中,轮廓运动(变形)依赖的是任意参数化曲线的导数。
曲线演化问题在数学上可以描述为:二维欧式空间R2中的一条光滑闭合的简单曲线沿着其法线方向以一定速度运动,形成以时间为变量的一簇曲线的过程。考虑运动曲线C(s,t)=(X(s,t),Y(s,t)),s为任意参数化变量,t为时间,用N表示描述曲线方向的单位法向矢量,k为描述曲线弯曲程度的曲率,曲线沿法向的演化可由下述偏微分方程表达:

其中,以v(k)被称为速度函数,它决定了曲线上每点的演化速度.曲线C上各点都沿其单位法向方向演化.要指出的是,沿任意方向运动的曲线总可以重参数化为方程(1)的形式,这是因为切向变形仅影响曲线的参数化,不影响其形状和几何属性。
几何活动轮廓模型的基本思想是将图像数据与变形速度相结合,以使演化曲线停止在对象边界上,这种演化采用水平集方法实现,因而,过去对几何模型的大多数研究集中在速度函数的设计上。
三、水平集方法
理论
水平集方法是一种新颖的求解几何曲线演化的方法,它以一种隐含的方式来表达平面闭合曲线或者立体闭合曲线,从而避免了对闭合曲线演化过程中的跟踪,将曲线演化转化成一个纯粹的求偏微分方程数值解问题。另外,水平集方法应用于几何曲线演化时,避免了演化曲线的参数化过程,这样曲线的拓扑结构的变化,即分裂或合并,就变得非常自然。因此,近年来水平集方法逐渐成为研究的热点,并被应用于图像分割,图像平滑,运动分割以及运动目标跟踪,甚至立体视觉和图像的恢复。Osher 和 Sethian[3][7]首次提出用 level set 法来模拟动态曲线和曲面,并以依赖于曲率的速度进化。令γ(t)为一个封闭的参数化曲线,γ(0)是沿着矢量场的法线方向进行传播的初始化曲线,速度依赖于曲率 k ,并给出了传播前沿的偏微分方程的解。假设φ(x,t),x∈R2,是一个矢量函数,在时间t 它的零level set是曲线γt 。进一步假设φ(x,0)=±d(x),其中 d(x)是从 t 到曲线γ0 的距离。如果 x在γ0 里面,就用正号表示,否则,就用负号。令Co§为欧氏平面的初始封闭曲线, C(p,t)是由Co§沿着欧氏法向量向内运动而产生的一系列曲线族。运动的速度认为是曲线曲率k 的矢量函数:

为了根据方程(3)实现曲线的进化,需要考虑利用 Lagrange 方法来产生位置矢量( x, y)= C§的相关运动方程。令φ(x, y,t):R2× [0,T)→R表示曲线C( p,t),那么,根据 level set方法,C( p,t)在时间 t由φ 的零 level set 点所组成:
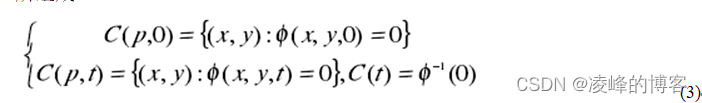
令φt 为φ对时间的偏微分,由求导的链式法则有:
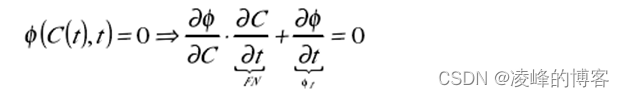
法矢量N =−(∇φ)/|∇φ|,把它代入方程(5),得到φ 的运动方程:
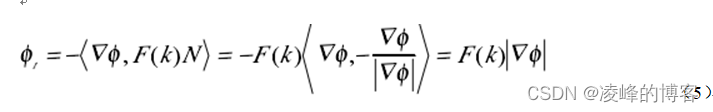
曲线的曲率值可以直接从 level set 函数中估计出来。容易看出 level set 函数沿着C ( p,t)都是同样的值,所以所有的微分都为零(与阶数无关)。对弧长求二阶偏导,得到下面的方程:
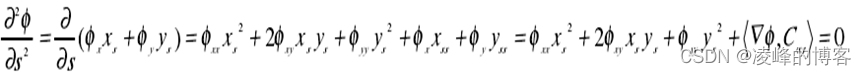
由 Cxy=(xss,yss)=kN,而法向量N=(-ys,xs)= −(∇φ)/|∇φ|,那么:
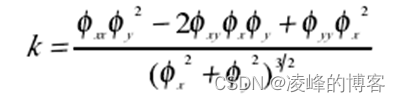
数值解格式
为了实现曲线传播的 level set 方法,必须利用数值近似来求解,一般用有限差分法,使定义在连续空间的偏微分方程能有效地在离散空间解决问题,并具有较强的鲁棒性。
在估计运动方程中出现的法向量、梯度向量和曲率值时,需要用到 level set 函数的一阶和二阶微分,所以要对其利用数值格式进行近似求解。level set 方程 φt = F|∇φ|可以表达成更一般的形式:φt+ H (φx,φy)=0,其中的函数 H (⋅)是哈密尔顿函数。接下去定义六个算子:
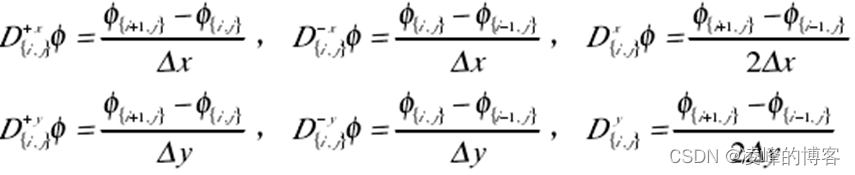
一种最简单的数值格式是:

四、水平集方法的关键问题
(l)水平集函数的初始化
通常初始化水平集函数φ(x,y,t)符号离函数d(x,y),其计算量一般较大。因此,如
何快速稳定地计算任意闭合曲面的d(x,y),对于提高水平集方法的效率和稳定性至关重要。
(2)水平集函数的重新初始化
水平集函数通常取为由初始曲线生成的符号距离函数,并且水平集函数在迭代过程中可能发生退化,使它不再保持为符号距离函数,而水平集函数一旦发生退化,则无法得到正确的分割结果。因此为了防止其退化,必须重新初始化水平集函数。保证水平集函数接近符号距离函数,从而保证数值解法的稳定性。符号距离函数必对所有的x,y满足|∇φ|=l,除了保持零水平集和初始化前一样外,重新初始化过程将在所有点上改变水平集函数。因此重新初始化并不改变区域ω和Q\ω重新初始化过程将通过解决一个关于φ(x,y,t)的偏微分方程:
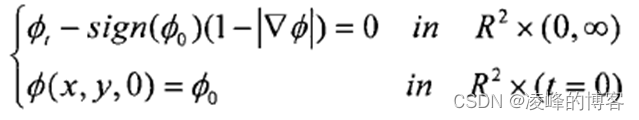
其中φ0为需要重新初始化的函数,这个方程将把函数转化为符号距离函数,并保证零水平集不变。但频繁的执行重新初始过程,不仅会影响水平集函数的演化速度,而且数值误差使零水平集定位不准。因此,如何在演化的过程中保持水平集为符号距离函数这一性质,而无需重新初始化成为当今研究热点。
(3)速度的延拓
水平集的速度函数F,而不仅仅是零水平集上的速度函数,但一般情况下,F只在零水平集上有定义,因此,需要将其延拓到整个解域。尽管已有许多方法对其进行拓展研究,但应用这些拓展速度函数的水平集函数演化方法会失去作为符号函数的特性,从而引起曲率和法向量计算的误差。因此,这些方案往往要求将水平集函数重新初始化为符号距离函数。Adalsteinsson和sethian[83J提出了一种新方法克服了上述不足,该方法是将速度函数拓展问题转化为一个边界值问题,并可通过快速行进法有效解决。Adalsteinsson和sethian指出无需重新初始化的速度函数应满足如下条件:
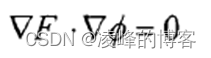

五、总结
水平集方法将二维闭合曲线或三维闭合曲面的演化问题转化为高维空间中水平集函数曲面演化的隐含方式来求解,适应于对拓扑结构变化的处理,其计算精度高,算法稳定,因而得到广泛应用。近几年来提出的算法大多数是多种算法相结合,但是采取什么样的结合方式才能充分利用各种算法的优点,取得准确的分割效果是人们关注和研究的问题,有待于今后继续研究,以得到更加成熟和适用临床的分割方法"
参考文献
[1] Zhu S, Yuille A. Region competition: Unifying Snakes, region growing, and Bayes/MDL for multi-band image segmentation [A]. International
Conference on Computer Vision (ICCV95) [C]. 1995, 416-423.
[2] Ravikanth Malladi, James A Sethian, Baba C Vemuri. Shape modeling with Front Propagation: A Level Set Approach [J]. IEEE Trans. on
pattern analysis and machine intellegence, 1995-02.
[3] Sethian. J A Level Set Methods [M]. UK: Cambridge University Press, 1996.
[4]QiangjunXie,XufengChen,LiMa,ZekuiZhou.Segmentation for CT image based on improvedlevelsetapproaeh[C],ImageandSignalProeessing,2008.CISP.08.Congress,2008,3:725一728.
[5]孟令旗,林财兴,崔芳芳,骆建珍.基于混合瑞利分布的三维医学图像分割算法[J], 计算机应用与软件,2009,26(l):236一239.
[7] Osher S, Sethian J A. Front propagating with curvature-Dependent Speed: Algorithm Based on Hamilton-Jacobi Formulation [J]. J. ofComputational physics, 1988, 79: 12-49 .
[8].罗嘉,张建伟,陈允杰.结合均值聚类的窄带水平集曲线演化[J],计算机应用与软件,2007,24(7):91一93.
[9] M. Kass, A. Witkin, and D. Terzopoulos, “Snakes: Active contourmodels,”Int. J. Comput. Vis., vol. 1, no. 4, pp. 321–331, Jan. 1987
[10] C. Xu, A. Yezzi, and J. Prince, “On the relationship between parametric and geometric active contours,” inProc. 34th Asilomar Conf. Signals, Syst., Comput., Pacific Grove, CA, Oct. 2000, pp. 483–489
相关文章:

基于 Level set 方法的医学图像分割
摘 要 医学图像分割是计算机辅助诊断系统设计中的关键技术。对于医学图像分割问题,它一般可分为两部分:(l)图像中特定目标区域(器官或组织)的识别;(2)目标区域完整性的描述与提取。相比于其他图像,医学图像的复杂性和多样性,使得传统的基于底层图像信息的分割方法很难取得好的…...
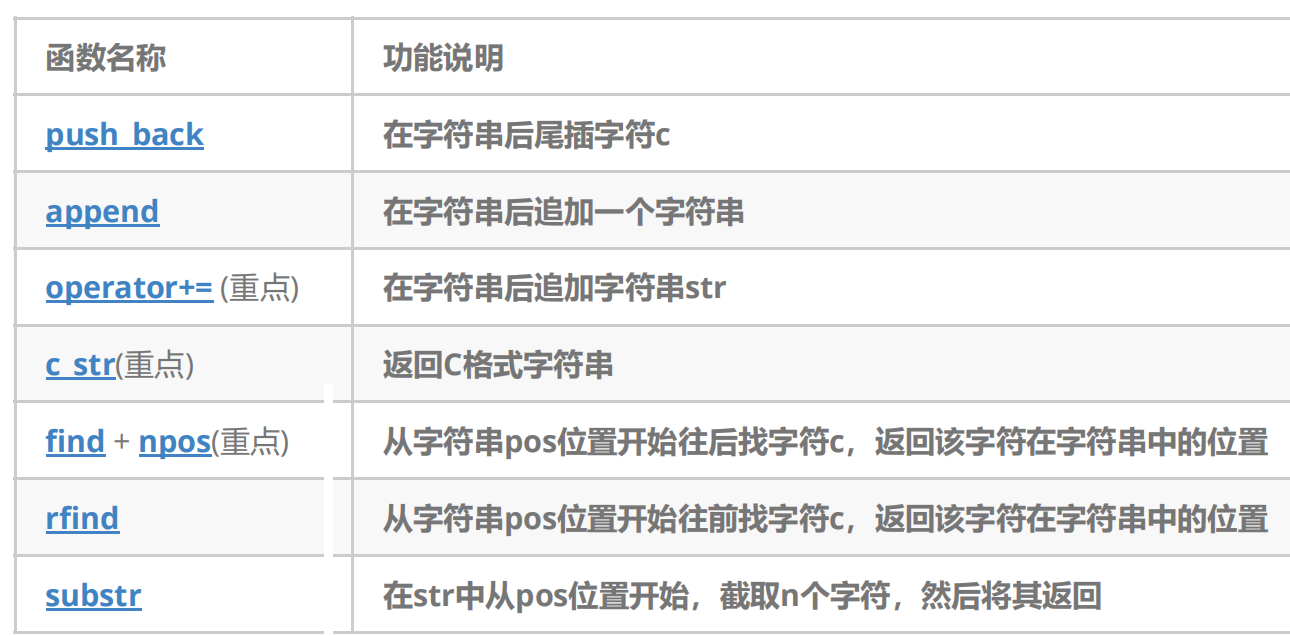
【C++入门】C++ STL中string常用函数用法总结
目录 前言 1. string使用 2. string的常见构造 3. string类对象的访问及遍历 迭代器遍历: 访问: 4. string类对象的容量操作 4.1 size和length 4.2 clear、empty和capacity 4.3 reserve和resize reserve resize 5. string类对象的修改操作 push_back o…...

Rust变量、常量声明与基本数据类型
Rust是一门系统级别的编程语言,注重安全性、性能和并发。在这篇博客中,我们将介绍Rust中的变量、常量声明以及基本数据类型,并通过示例说明每一种类型的用法。 变量声明 在Rust中,使用 let 关键字声明变量。变量默认是不可变的&…...
【MATLAB】 SSA奇异谱分析信号分解算法
有意向获取代码,请转文末观看代码获取方式~ 1 基本定义 SSA奇异谱分析(Singular Spectrum Analysis)是一种处理非线性时间序列数据的方法,可以对时间序列进行分析和预测。 它基于构造在时间序列上的特定矩阵的奇异值分解&#…...

Nginx+Tomcat负载均衡、动静分离以及Nginx负载均衡和四层代理
目录 NginxTomcat负载均衡、动静分离 Nginx 负载均衡模式: Nginx 四层代理配置: NginxTomcat负载均衡、动静分离 Nginx 服务器:192.168.80.10:80 Tomcat服务器1:192.168.80.100:80 Tomcat服务器2:192.168.80.101:80…...

Vue3中provide,inject使用
一,provide,inject使用: 应用场景:向孙组件传数据 应用Vue3碎片: ref,reactive,isRef,provide, inject 1.provide,inject使用 a.爷组件引入 import {ref,provide} from vue const drinkListre…...

Django命令模块
这篇文章我们主要来介绍一下关于 Django 的命令模块,我们经常会使用到,比如以下几个常用的命令,都属于 Django 的命令模块: python manage.py makemigrations python manage.py migrate python manage.py startapp python manage…...
【linux驱动开发】在linux内核中注册一个杂项设备与字符设备以及内核传参的详细教程
文章目录 注册杂项设备驱动模块传参注册字符设备 开发环境: windows ubuntu18.04 迅为rk3568开发板 注册杂项设备 相较于字符设备,杂项设备有以下两个优点: 节省主设备号:杂项设备的主设备号固定为 10,在系统中注册多个 misc 设备驱动时&…...
)
Golang条件编译 | 获取系统的磁盘空间内存占用demo | gopsutil/disk库(跨平台方案)
文章目录 一、Golang条件编译1. 构建标签( Build tags)2. 文件后缀(File suffixes) 二、GO golang 获取磁盘空间 条件编译思路 三、【推荐】使用github.com/shirou/gopsutil/disk这个库,如何获取机器下不同磁盘分区的内容 一、Golang条件编译…...

22/76-池化
池化(最大池化层:选每个kernel中最大的数) 填充、步幅、多个通道: 池化层与卷积层类似,都具有填充和步幅。 没有可学习的参数。 在每个输入通道应用池化层以获得相应的输出通道。 输出通道数输入通道数。 平均池化层…...
江科大STM32 下
目录 ADC数模转换器DMA直接存储器存取USART串口9-2 串口发送接受9-3 串口收发HEX数据包 I2C(mpu6050陀螺仪和加速度计)SPI协议10.1 SPI简介W25Q64简介10.3 SPI软件读写W25Q6410.4 SPI硬件读写W25Q64 BKP、RTC11.0 Unix时间戳11.1 读写备份寄存器BKP11.2 RTC实时时钟 十二、PWR1…...
利用HTML和CSS实现的浮动布局
代码如下 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><style>*{m…...

2024年第十届控制、自动化与机器人国际会议(ICCAR 2024)即将召开!
2024年4月27~29日 新加披 会议官网:10th-ICCAR 2024https://iccar.org/index.html 第十届控制、自动化和机器人国际会议将于2024年4月27-29日在新加坡举办。本次会议由新加坡电子学会,IEEE机器人和自动控制协会和IEEE联合主办,并得到北京航空…...
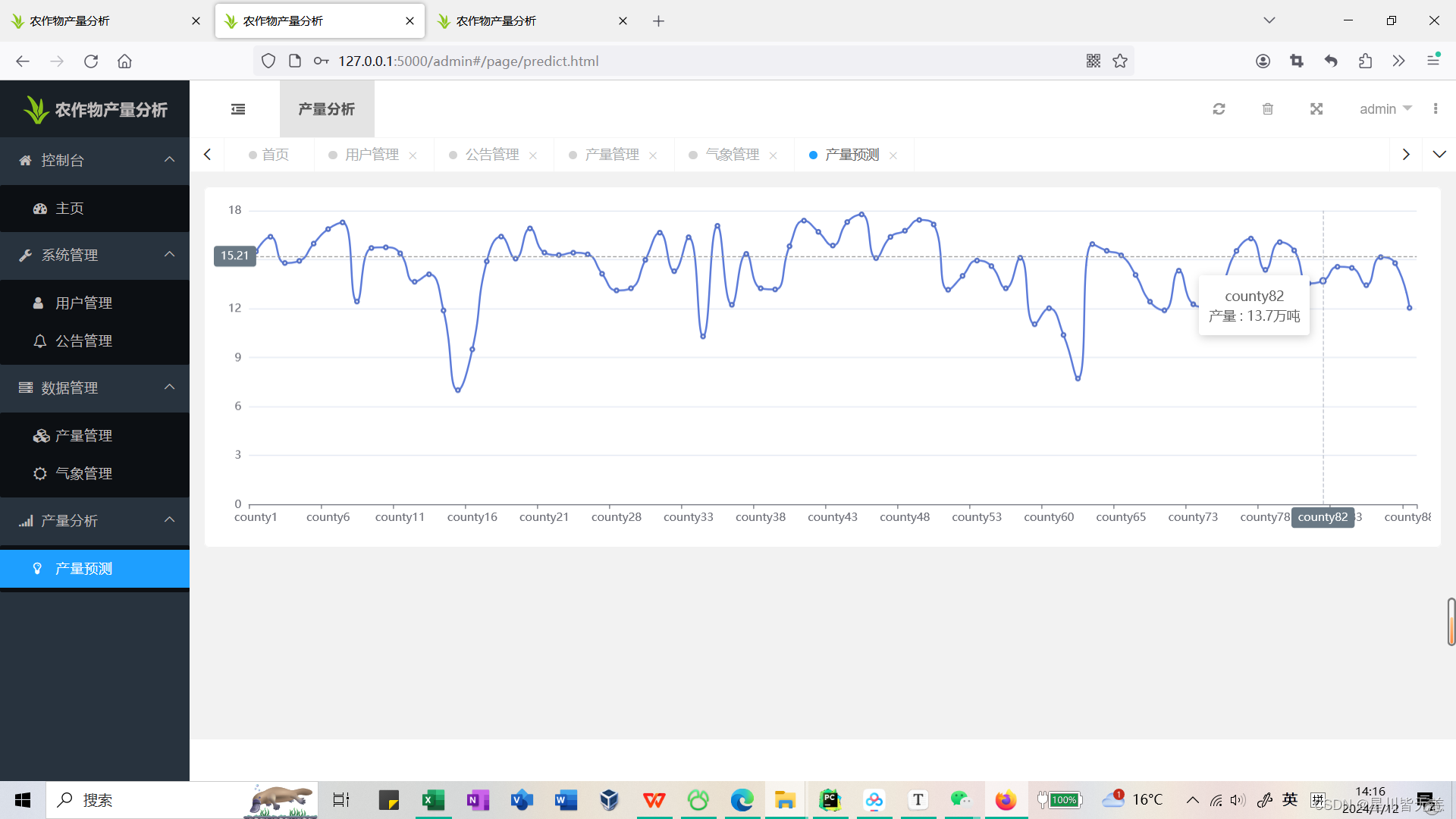
基于python集成学习算法XGBoost农业数据可视化分析预测系统
文章目录 基于python集成学习算法XGBoost农业数据可视化分析预测系统一、项目简介二、开发环境三、项目技术四、功能结构五、功能实现模型构建封装类用于网格调参训练模型系统可视化数据请求接口模型评分 0.5*mse 六、系统实现七、总结 基于python集成学习算法XGBoost农业数据可…...
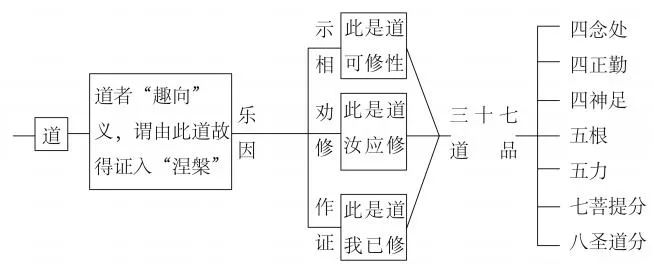
第29集《佛法修学概要》
丁三、声闻乘 分二:戊一、释义;戊二、四谛法;戊三、结示 请大家打开讲义第八十二页。我们看丁三,声闻乘。 在祖师大德的判教当中,把我们整个大乘的成佛之道分成了三个部分:第一个是安乐道,第…...

奥伦德光电耦合器5G通信领域及其相关领域推荐
光电耦合器是以光为媒介传输电信号的一种电-光-电转换器件。由于该器件使用寿命长、工作温度范围宽,所以在过程控制、工业通信、家用电器、医疗设备、通信设备、计算机以及精密仪器等方面有着广泛应用在当前工艺技术持续发展与提升的过程中,其工作速度、…...

机器学习算法 - 马尔可夫链
马尔可夫链(Markov Chain)可以说是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测、语音识别方面都有着极其广泛的应用 > The future is independent of the past given the present 未来独立于过去ÿ…...

Linux下防火墙相关命令整理
目录 一.前言二.相关命令整理 一.前言 这篇文章简单整理一下Linux系统中防火墙相关命令。 二.相关命令整理 开启防火墙 systemctl start firewalld关闭防火墙 systemctl stop firewalld重启防火墙 systemctl restart firewalld开机启用防火墙 systemctl enable firewall…...

Python八股文总结
一. Python基本数据结构有哪四种?区别是什么? 列表(List)元组(Tuple)字典(Dictionary)集合(Set) 区别主要在于它们的可变性(是否可以修改&#x…...
计算机导论05-计算机网络
文章目录 计算机网络基础计算机网络概述计算机网络的概念计算机网络的功能计算机网络的组成 计算机网络的发展计算机网络的类型 网络体系结构网络互联模型OSI/RM结构与功能TCP/IP结构模型TCP/IP与OSI/RM的比较 网络地址与分配IP地址构成子网的划分IPv6 传输介质与网络设备网络传…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
