【论文阅读】Deep Graph Contrastive Representation Learning
目录
- 0、基本信息
- 1、研究动机
- 2、创新点
- 3、方法论
- 3.1、整体框架及算法流程
- 3.2、Corruption函数的具体实现
- 3.2.1、删除边(RE)
- 3.2.2、特征掩盖(MF)
- 3.3、[编码器](https://blog.csdn.net/qq_44426403/article/details/135443921)的设计
- 3.3.1、直推式学习
- 3.4、损失函数的定义
- 3.5、评估
- 3.6、理论动机
- 3.6.1、最大化目标函数等价于最大化互信息的下界
- 3.6.2、三重损失
- 3.7、实验参数设置
- 4、代码实现
- 4.1、RE and MF
- 4.2、encorder
- 4.3、GRACE
- 4.4、loss
0、基本信息
- 作者:Yanqiao Zhu Yichen Xu
- 文章链接:Deep Graph Contrastive Representation Learning
- 代码链接:Deep Graph Contrastive Representation Learning
1、研究动机
-
现实世界中,图的标签数量较少,尽管GNNs蓬勃发展,但是训练模型时标签的可用性问题也越来越受到关心。
-
传统的无监督图表征学习方法,例如DeepWalk和node2vec,以牺牲结构信息为代价过度强调邻近信息
-
基于局部-全局互信息最大化框架的[[DGI]]模型,要求readout函数是单射的具有局限性,并且对节点特征随机排列,当特征矩阵稀疏时,不足以生成不同的上下文信息,导致难以学习对比目标
本文提出的GRACE模型:首先,通过移除边和掩盖特征生成两个视图,然后最大化两个视图中结点嵌入的一致性。
2、创新点
- 结点级图对比学习框架
- 提出新的Corruption Function:删除边和特征掩盖
3、方法论
3.1、整体框架及算法流程
- 首先,通过Corruption函数在原始图 G G G的基础上生成两个视图 G ~ 1 \tilde{G}_1 G~1和 G ~ 2 \tilde{G}_2 G~2;
- 其次,通过编码器函数 f f f,生成两个视图的结点嵌入表征, U = f ( G ~ 1 ) U=f(\tilde{G}_1) U=f(G~1)和 V = f ( G ~ 2 ) V=f(\tilde{G}_2) V=f(G~2);
- 计算对比目标函数 J \mathcal{J} J;
- 通过随机梯度下降更新参数;
GRACE的整体框架如下图所示:

3.2、Corruption函数的具体实现
视图的生成是对比学习方法的关键组成部分,不同视图为每个节点提供不同的上下文,本文依赖不同视图中结点嵌入之间对比的对比方法,作者在结构和属性两个层次上破坏原始图,这为模型构建了不同的节点上下文,分别是删除边和掩蔽结点特征。
3.2.1、删除边(RE)
随机删除原图中的部分边。
首先,采样一个随机掩盖矩阵 R ~ ∈ { 0 , 1 } N × N \tilde{R}\in \{0,1\}^{N \times N} R~∈{0,1}N×N,矩阵中的每个元素服从伯努利分布,即 R ~ ∼ B ( 1 − p r ) \tilde{R}\sim \mathcal{B}(1-p_r) R~∼B(1−pr), p r p_r pr是每条边被移除的概率;其次,用得到地掩盖矩阵与原始邻接矩阵做Hadamard积,最终得到的邻接矩阵为:
A ~ = A ∘ R ~ \tilde{A}=A\circ \tilde{R} A~=A∘R~
注意,上式为Hadamard积。
3.2.2、特征掩盖(MF)
再结点特征中用零随机地掩盖部分特征。
首先,采样一个随机向量 m ~ ∈ { 0 , 1 } F \tilde{m}\in\{0,1\}^F m~∈{0,1}F,向量的每个元素来自于伯努利分布,即 m ~ ∼ B ( 1 − p m ) \tilde{m}\sim \mathcal{B}(1-p_m) m~∼B(1−pm), p r p_r pr是元素被掩盖的概率;其次,用得到地掩盖向量与原始特征做Hadamard积,最终得到的特征矩阵为:
X ~ = [ x 1 ∘ m ~ ; x 2 ∘ m ~ ; . . . ; x N ∘ m ~ ; ] \tilde{X}=[x_1 \circ\tilde{m};x_2 \circ\tilde{m};...;x_N \circ\tilde{m};] X~=[x1∘m~;x2∘m~;...;xN∘m~;]
注意, [ . ; . ] [.;.] [.;.]是连接运算符。
3.3、编码器的设计
针对不同任务,transductive learning、inductive learning on large graphs和inductive learning on multiple graphs,设计不同的编码器。这里仅仅列出transductive learning的编码器设计,其他任务编码器的设计请阅读原文4.2节实验设置。
3.3.1、直推式学习
直推式学习采用了一个两层的GCN作为编码器。编码器 f f f的形式如下:
G C i ( X , A ) = σ ( D ^ 1 2 A ^ D ^ 1 2 X W i ) GC_i(X,A)=\sigma(\hat{D}^{\frac{1}{2}}\hat{A}\hat{D}^{\frac{1}{2}}XW_i) GCi(X,A)=σ(D^21A^D^21XWi)
f ( X , A ) = G C 2 ( G C 1 ( X , A ) , A ) f(X,A)=GC_2(GC_1(X,A),A) f(X,A)=GC2(GC1(X,A),A)
其中, A ^ = A + I \hat{A}=A+I A^=A+I, D ^ \hat{D} D^为 A ^ \hat{A} A^的度矩阵, σ ( . ) \sigma(.) σ(.)为激活函数,例如 R e L U ( . ) = m a x ( 0 , . ) \mathrm{ReLU}(.)=max(0,.) ReLU(.)=max(0,.), W i W_i Wi为可训练的权重矩阵。
3.4、损失函数的定义
对比目标,即判别器,是将两个来自不同视图相同结点的嵌入与其他结点区分开来,最大化嵌入之间的结点级的一致性。
对于任意一个结点 v i v_i vi,在第一个视图中的嵌入为 u i \mathbf{u}_i ui,被视作锚;在另外一个视图中的嵌入为 v i \mathbf{v}_i vi,形成正样本,两个视图中出 v i v_i vi之外的结点嵌入被视为负样本。
简单而言,正样本:同一结点在不同视图的嵌入被视作正样本对;负样本包含两类:(1)intra-view:同一视图中的不同结点对(2)inter-view:不同视图中的不同结点对。
判别函数定义为 θ ( u , v ) = s ( g ( u ) , g ( v ) ) \theta(u,v)=s(g(u),g(v)) θ(u,v)=s(g(u),g(v)), s s s为cosine相似度,g为非线性映射,例如两层的MLP。
综上所述,目标函数定义为:
ℓ ( u i , v i ) = log e θ ( u i , v i ) / τ e θ ( u i , v i ) / τ ⏟ the positive pair + ∑ k = 1 N 1 [ k ≠ i ] e θ ( u i , v k ) / τ ⏟ inter-view negaive pairs + ∑ k = 1 N 1 [ k ≠ i ] e θ ( u i , u k ) / τ ⏟ intra-view negative pairs \ell(\boldsymbol{u}_i,\boldsymbol{v}_i)=\log\frac{e^{\theta(\boldsymbol{u}_i,\boldsymbol{v}_i)/\tau}}{\underbrace{e^{\theta(\boldsymbol{u}_i,\boldsymbol{v}_i)/\tau}}_{\text{the positive pair}}+\underbrace{\sum _ { k = 1 }^N\mathbb{1}_{[k\neq i]}e^{\theta(\boldsymbol{u}_i,\boldsymbol{v}_k)/\tau}}_{\text{inter-view negaive pairs}}+\underbrace{\sum _ { k = 1 }^N\mathbb{1}_{[k\neq i]}e^{\theta(\boldsymbol{u}_i,\boldsymbol{u}_k)/\tau}}_{\text{intra-view negative pairs}}} ℓ(ui,vi)=logthe positive pair eθ(ui,vi)/τ+inter-view negaive pairs k=1∑N1[k=i]eθ(ui,vk)/τ+intra-view negative pairs k=1∑N1[k=i]eθ(ui,uk)/τeθ(ui,vi)/τ
其中, 1 [ k ≠ i ] ∈ { 0 , 1 } \mathbb{1}_{[k\neq i]}\in\{0,1\} 1[k=i]∈{0,1}是一个指示函数,当且仅当 k ≠ i k \neq i k=i时定于1。两个视图是对称的,另一个视图定义类似 ℓ ( v i , u i ) \ell(\boldsymbol{v}_i,\boldsymbol{u}_i) ℓ(vi,ui),最后,要最大化的总体目标被定义为:
J = 1 2 N ∑ i = 1 N [ ℓ ( u i , v i ) + ℓ ( v i , u i ) ] \mathcal{J}=\dfrac{1}{2N}\sum_{i=1}^N\left[\ell(\boldsymbol{u}_i,\boldsymbol{v}_i)+\ell(\boldsymbol{v}_i,\boldsymbol{u}_i)\right] J=2N1i=1∑N[ℓ(ui,vi)+ℓ(vi,ui)]
3.5、评估
类似于DGI中的线性评估方案,模型首先以无监督的方式训练,得到的嵌入被用来训练逻辑回归分类器并做测试。
3.6、理论动机
3.6.1、最大化目标函数等价于最大化互信息的下界
定理1说明了目标函数 J \mathcal{J} J是InfoNCE目标函数的一个下界,而InfoNCE评估器是MI(即互信息)的下界,所以 J ≤ I ( X ; U , V ) \mathcal{J} \le I(X;U,V) J≤I(X;U,V)。
所以,最大化目标函数 J \mathcal{J} J等价于最大化输入节点特征和学习节点表示之间的互信息 I ( X ; U , V ) I(X;U,V) I(X;U,V)的下界
3.6.2、三重损失
定理2说明了最小化目标函数与最大化三重损失一致。更详细的证明请看原文。
triplet Loss是深度学习中的一种损失函数,用于训练差异性较小的样本,如人脸等。在人脸识别领域,triplet loss常被用来提取人脸的embedding。 输入数据是一个三元组,包括锚(Anchor)例、正(Positive)例、负(Negative)例,通过优化锚示例与正示例的距离小于锚示例与负示例的距离,实现样本的相似性计算。
3.7、实验参数设置
| Dataset | p m , 1 p_{m,1} pm,1 | p m , 2 p_{m,2} pm,2 | p r , 1 p_{r,1} pr,1 | p r , 2 p_{r,2} pr,2 | lr | wd | epoch | hidfeat | activation |
|---|---|---|---|---|---|---|---|---|---|
| Cora | 0.3 | 0.4 | 0.2 | 0.4 | 0.005 | 1e-5 | 200 | 128 | ReLU |
| Citeseer | 0.3 | 0.2 | 0.2 | 0.0 | 0.001 | 1e-5 | 200 | 256 | PReLU |
| Pubmed | 0.0 | 0.2 | 0.4 | 0.1 | 0.001 | 1e-5 | 1500 | 256 | ReLU |
4、代码实现
完整代码见
链接:https://pan.baidu.com/s/1g9Rhe1EjxBZ0dFgOfy3CSg
提取码:6666
4.1、RE and MF
from dgl.transforms import DropEdge
#RE
#随机删除边——使用dgl内建库DropEdge
#MF
#随机掩盖特征
def drop_feature(x, drop_prob):drop_masks=[]for i in range(x.shape[0]):drop_mask = torch.empty(size= (x.size(1),) ,dtype=torch.float32,device=x.device).uniform_(0, 1) < drop_probdrop_masks.append(drop_mask)x = x.clone()for i,e in enumerate(drop_masks):x[i,e] = 0return x4.2、encorder
import dgl
import torch.nn as nn
from dgl.nn.pytorch import GraphConv
from model.GCNLayer import GCNLayerclass Encoder(nn.Module):def __init__(self, infeat: int, outfeat: int, act_func,base_model=GraphConv, k: int = 2):super(Encoder, self).__init__()self.base_model = base_modelassert k >= 2self.k = kself.convs = nn.ModuleList()self.convs.append(base_model(infeat, 2 * outfeat))for _ in range(1, k-1):self.convs.append(base_model(2 * outfeat, 2 * outfeat))self.convs.append(base_model(2 * outfeat, outfeat))self.act_func = act_funcdef forward(self, g, x ):#g = dgl.add_self_loop(g)for i in range(self.k):x = self.act_func(self.convs[i](g,x))return x
4.3、GRACE
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from dgl.nn.pytorch import GraphConv
from model.encoder import Encoder
class GRACE(nn.Module):def __init__(self,infeat,hidfeat,act_func,k=2) -> None:super(GRACE,self).__init__()self.encoder = Encoder(infeat,hidfeat,act_func,base_model=GraphConv,k=k)def forward(self,g,x):z =self.encoder(g,x)return z
4.4、loss
import torch
import torch.nn as nn
import torch.nn.functional as F
class LossFunc(nn.Module):def __init__(self, infeat,hidfeat,outfeat,tau) -> None:super(LossFunc,self).__init__()self.tau = tauself.layer1 = nn.Linear(infeat,hidfeat)self.layer2 = nn.Linear(hidfeat,outfeat)def projection(self,x):x = F.elu(self.layer1(x))x = self.layer2(x)return xdef sim(self,x,y):x = F.normalize(x)y = F.normalize(y)return torch.mm(x, y.t())def sim_loss(self,h1,h2):f = lambda x : torch.exp(x/self.tau)#exp(\theta(u_i,u_j)/tau)intra_sim = f(self.sim(h1,h1))#exp(\theta(u_i,v_j)/tau)inter_sim = f(self.sim(h1,h2))return -torch.log(inter_sim.diag() / (intra_sim.sum(1) + inter_sim.sum(1) - intra_sim.diag()))def forward(self,u,v):h1 = self.projection(u)h2 = self.projection(v)loss1 = self.sim_loss(h1,h2)loss2 = self.sim_loss(h2,h1)loss_sum = (loss1 + loss2) * 0.5res = loss_sum.mean()return res
相关文章:

【论文阅读】Deep Graph Contrastive Representation Learning
目录 0、基本信息1、研究动机2、创新点3、方法论3.1、整体框架及算法流程3.2、Corruption函数的具体实现3.2.1、删除边(RE)3.2.2、特征掩盖(MF) 3.3、[编码器](https://blog.csdn.net/qq_44426403/article/details/135443921)的设…...
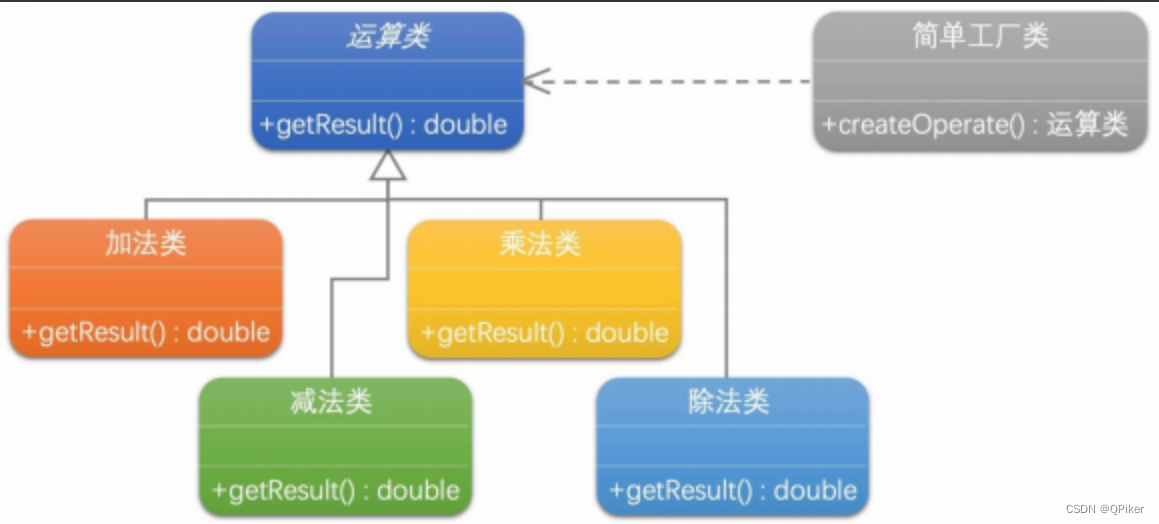
设计模式-简单工厂
设计模式-简单工厂 简单工厂模式是一个集中管理对象创建,并根据条件生成所需类型对象的设计模式,有助于提高代码的复用性和维护性,但可能会导致工厂类过于复杂且违反开闭原则。 抽象提取理论: 封装对象创建过程解耦客户端与产品…...
)
Django ORM 中的单表查询 API(1)
在 Django 中,对象关系映射(ORM)提供了一种功能强大、表现力丰富的数据库交互方式。ORM 允许开发人员使用高级 Python 代码执行数据库查询,从而更轻松地处理数据库实体。 下面,我们将探讨 Django ORM 中单表查询 API …...
电子雨html代码
废话不多说下面是代码: <!DOCTYPE html><html lang"en"><head><meta charset"UTF-8"><title>Code</title><style>body{margin: 0;overflow: hidden;}</style></head><body><c…...

xadmin基于Django的后台管理系统安装与使用
xadmin是基于Django的后台管理系统 官网:http://sshwsfc.github.io/xadmin/ github地址:https://github.com/sshwsfc/xadmin 安装方式 pip安装 pip install xadmin在setting配置中添加: INSTALLED_APPS [xadmin,crispy_forms, ]在urls.py…...

[go语言]输入输出
目录 知识结构 输入 1.Scan 编辑 2.Scanf 3.Scanln 4.os.Stdin --标准输入,从键盘输入 输出 1.Print 2.Printf 3.Println 知识结构 输入 为了展示集中输入的区别,将直接进行代码演示。 三者区别的结论:Scanf格式化输入&#x…...

【SpringBoot系列】AOP详解
🤵♂️ 个人主页:@香菜的个人主页,加 ischongxin ,备注csdn ✍🏻作者简介:csdn 认证博客专家,游戏开发领域优质创作者,华为云享专家,2021年度华为云年度十佳博主 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞👍🏻 收…...

openssl3.2 - 官方demo学习 - signature - rsa_pss_hash.c
文章目录 openssl3.2 - 官方demo学习 - signature - rsa_pss_hash.c概述笔记END openssl3.2 - 官方demo学习 - signature - rsa_pss_hash.c 概述 对私钥对明文做签名(摘要算法为SHA256) 用公钥对密文做验签(摘要算法为SHA256) 笔记 /*! \file rsa_pss_hash.c \note openss…...

Redis相关知识点
1.什么是Redis Redis (REmote DIctionary Server) 是用 C 语言开发的一个开源的高性能键值对(key-value)数据库,它支持网络,可基于内存亦可持久化,并提供多种语言的API。Redis具有高效性、原子性、支持多种数据结构、…...
嵌入式开发--STM32G4系列片上FLASH的读写
这个玩意吧,说起来很简单,就是几行代码的事,但楞是折腾了我大半天时间才搞定。原因后面说,先看代码吧: 读操作 读操作很简单,以32位方式读取的时候是这样的: data *(__IO uint32_t *)(0x080…...
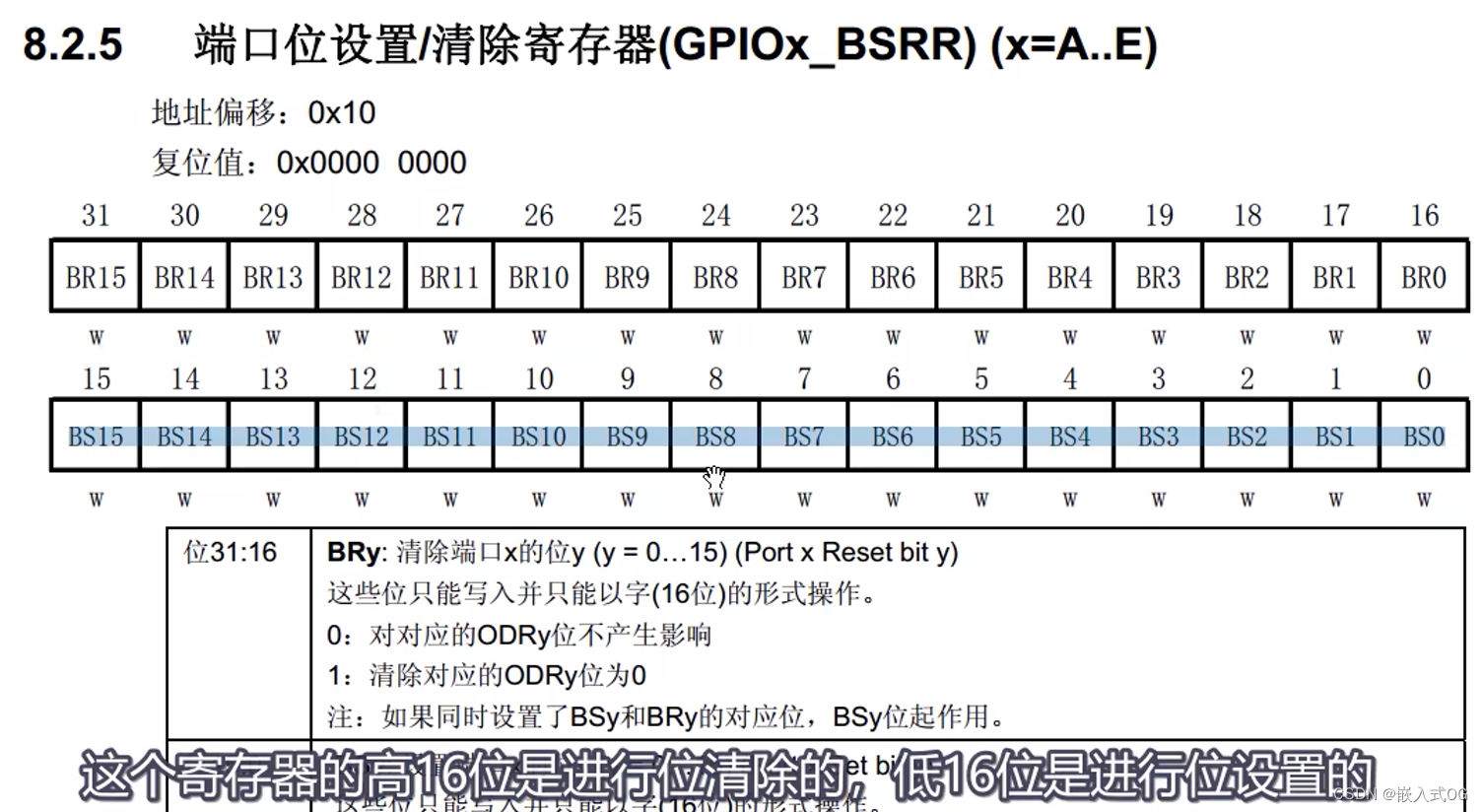
嵌入式-Stm32-江科大基于标准库的GPIO的八种模式
文章目录 一:GPIO输入输出原理二:GPIO基本结构三:GPIO位结构四:GPIO的八种模式道友:相信别人,更要一百倍地相信自己。 (推荐先看文章:《 嵌入式-32单片机-GPIO推挽输出和开漏输出》…...

2024年1月17日Arxiv热门NLP大模型论文:THE FAISS LIBRARY
Meta革新搜索技术!提出Faiss库引领向量数据库性能飞跃 引言:向量数据库的兴起与发展 随着人工智能应用的迅速增长,需要存储和索引的嵌入向量(embeddings)数量也在急剧增加。嵌入向量是由神经网络生成的向量表示&…...
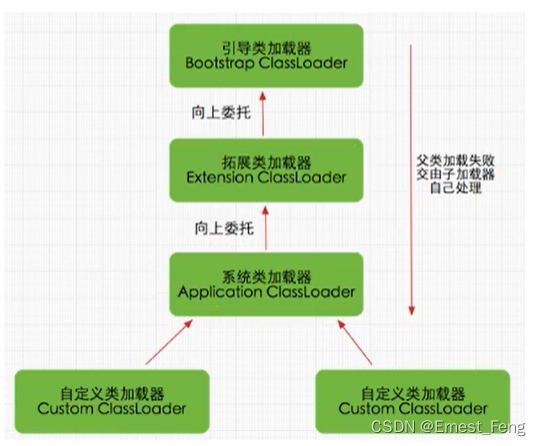
深度解析JVM类加载器与双亲委派模型
概述 Java虚拟机(JVM)是Java程序运行的核心,其中类加载器和双亲委派模型是JVM的重要组成部分。本文将深入讨论这两个概念,并解释它们在实际开发中的应用。 1. 什么是类加载器? 类加载器是JVM的一部分,负…...
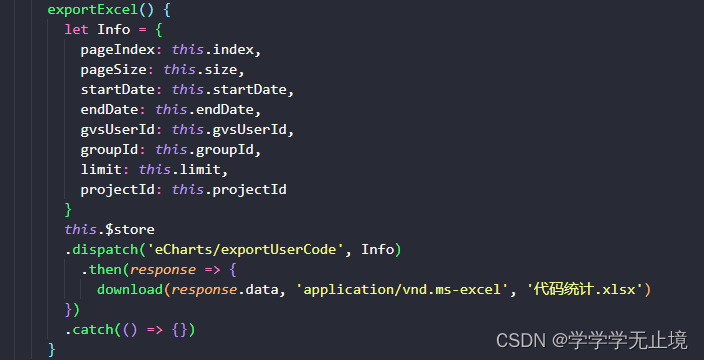
前端下载文件流,设置返回值类型responseType:‘blob‘无效的问题
前言: 本是一个非常简单的请求,即是下载文件。通常的做法如下: 1.前端通过Vue Axios向后端请求,同时在请求中设置响应体为Blob格式。 2.后端相应前端的请求,同时返回Blob格式的文件给到前端(如果没有步骤…...
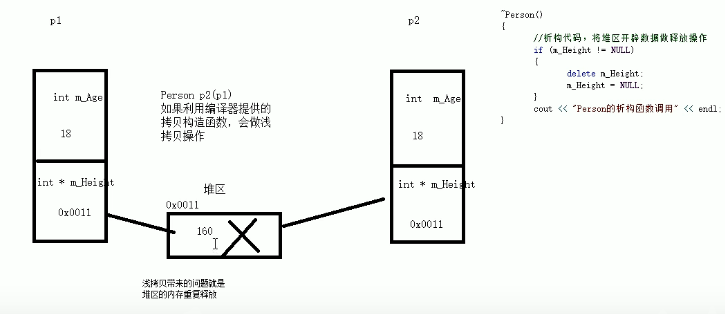
C++核心编程——类和对象(一)
本专栏记录C学习过程包括C基础以及数据结构和算法,其中第一部分计划时间一个月,主要跟着黑马视频教程,学习路线如下,不定时更新,欢迎关注。 当前章节处于: ---------第1阶段-C基础入门 ---------第2阶段实战…...

脱模斜度是什么意思,为什么要有脱模斜度,没有斜度不行吗?
问题描述:脱模斜度是什么意思,为什么要有脱模斜度,没有斜度不行吗? 问题解答: 脱模斜度是指在模具中的零件在脱模(从模具中取出)过程中相对于模具开合方向的倾斜程度。在模具设计和制造中&…...

【现代密码学】笔记9-10.3-- 公钥(非对称加密)、混合加密理论《introduction to modern cryphtography》
【现代密码学】笔记9-10.3-- 公钥(非对称加密)、混合加密理论《introduction to modern cryphtography》 写在最前面8.1 公钥加密理论随机预言机模型(Random Oracle Model,ROM) 写在最前面 主要在 哈工大密码学课程 张…...
牛客-寻找第K大、LeetCode215. 数组中的第K个最大元素【中等】
文章目录 前言牛客-寻找第K大、LeetCode215. 数组中的第K个最大元素【中等】题目及类型思路思路1:大顶堆思路2:快排二分随机基准点 前言 博主所有博客文件目录索引:博客目录索引(持续更新) 牛客-寻找第K大、LeetCode215. 数组中的第K个最大元…...
MySQL的各种日志
目录 一、错误日志 二、二进制日志 1、介绍 2、作用 3、相关信息 4、日志格式 5、查看二进制文件 6、二进制日志文件删除 三、查询日志 四、慢日志 一、错误日志 记录MySQL在启动和停止时,以及服务器运行过程中发生的严重错误的相关信息,当数据库…...
rust跟我学六:虚拟机检测
图为RUST吉祥物 大家好,我是get_local_info作者带剑书生,这里用一篇文章讲解get_local_info是怎么检测是否在虚拟机里运行的。 首先,先要了解get_local_info是什么? get_local_info是一个获取linux系统信息的rust三方库,并提供一些常用功能,目前版本0.2.4。详细介绍地址:…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
