数据结构--排序
参考【算法】排序算法之希尔排序 - 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/122632213
1. 排序的定义
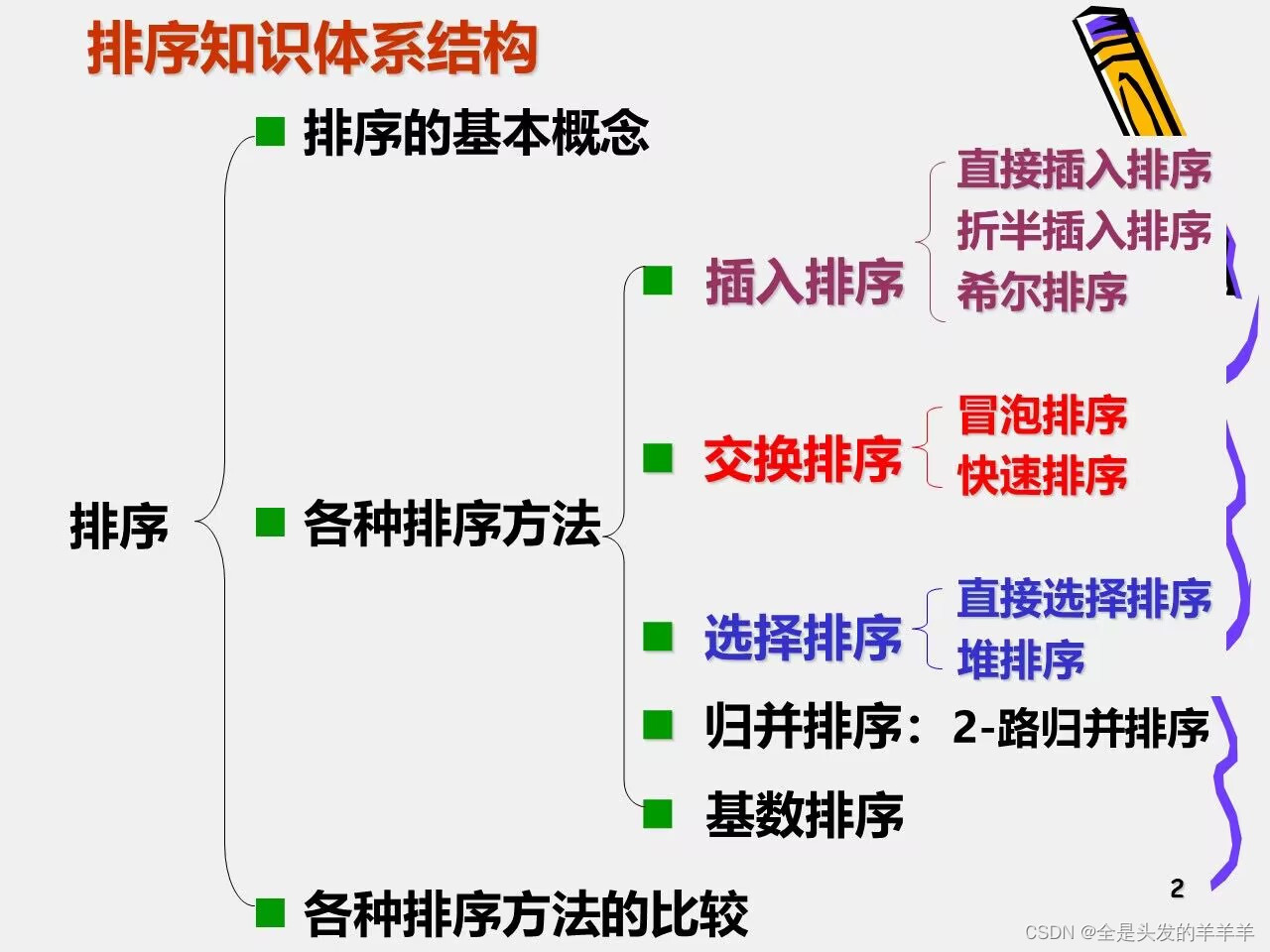
2. 插入排序
2.1 直接插入排序
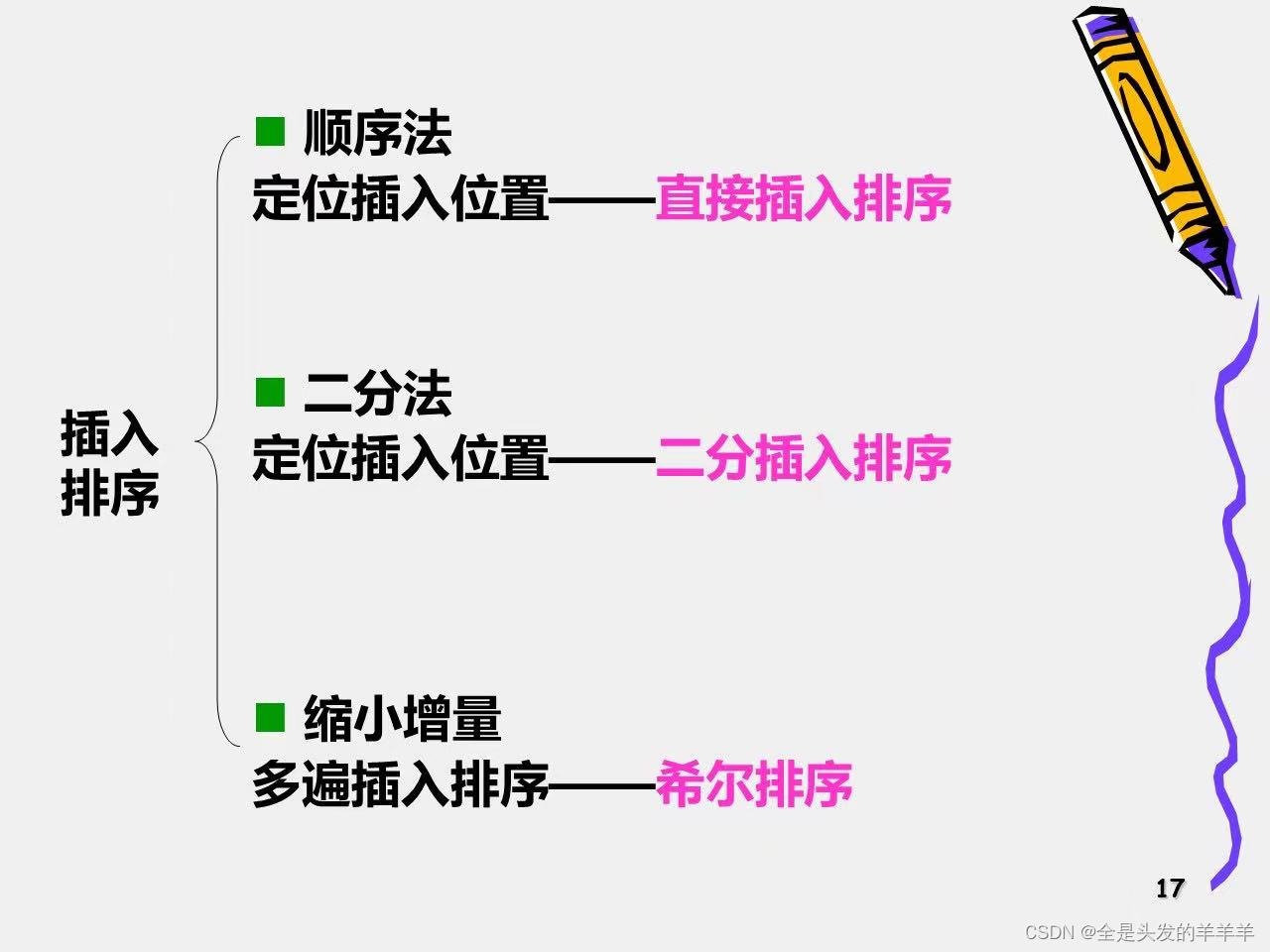 在插入第i(i>1)个记录时,前面的i-1个记录已经排好序
在插入第i(i>1)个记录时,前面的i-1个记录已经排好序
void insertSort(int r[],int n)
{for(int i=2;i<=n;i++){if(r[i]<r[i-1]{r[0]=r[i];j=i-1;while(r[0]<r[j]){r[j+1]=r[j];j=j-1;}r[j+1]=r[j];j=j-1;}r[j+1]=r[0];}}
}2.2 折半插入排序
用折半查找方法确定插入位置的排序
3. 希尔排序
缩小增量,多遍插入排序
基本思想:
将整个待排序记录分割成若干个子序列,在子序列内分别进行直接插入排序,待整个序列中的记录基本有序时,对全体记录进行直接插入排序。
分割待排序记录目的:
1.减少待排序记录
2.使整个序列向基本有序发展
希尔排序的特点:
1.一次移动,移动位置较大,跳跃式地接近排序后的最终位置
2.最后一次只需要少量移动
3.增量序列必须是递减的,最后一个必须是1
4.增量序列应该是互质的
示例图:
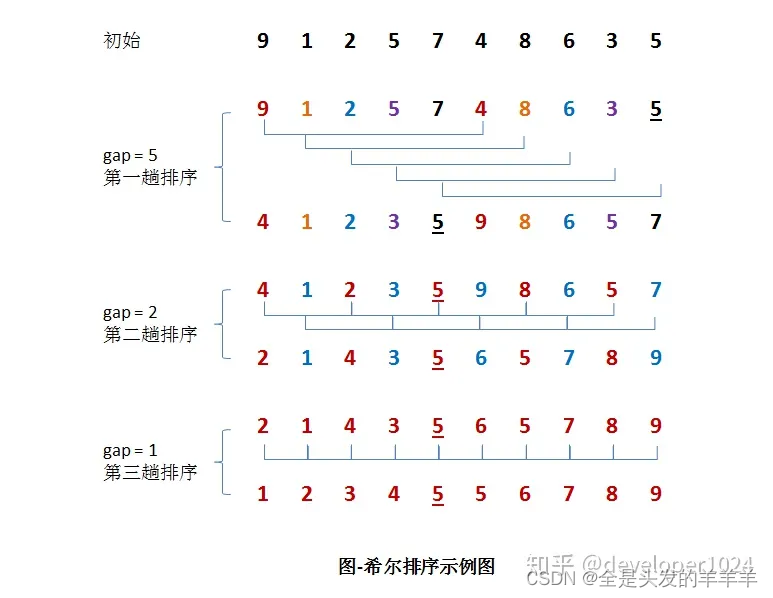
假设有一组{9, 1, 2, 5, 7, 4, 8, 6, 3, 5}无需序列。
第一趟排序: 设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。接下来,按照直接插入排序的方法对每个组进行排序。
第二趟排序:
将上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为2组。按照直接插入排序的方法对每个组进行排序。
第三趟排序:
再次把 gap 缩小一半,即gap3 = gap2 / 2 = 1。 这样相隔距离为1的元素组成一组,即只有一组。按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。
注:需要注意一下的是,图中有两个相等数值的元素5和5。我们可以清楚的看到,在排序过程中,两个元素位置交换了。
代码实现
void shell_sort(int arr[], int len) {int gap, i, j;int temp;for (gap = len >> 1; gap > 0; gap >>= 1)for (i = gap; i < len; i++) {temp = arr[i];for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)arr[j + gap] = arr[j];arr[j + gap] = temp;}
}算法评价
1.希尔排序的效率取决于增量值gap的选取,时间复杂度并不是一个定值。
2.开始时,gap取值较大,子序列中的元素较少,排序速度快,克服了直接插入排序的缺点;其次,gap值逐渐变小后,虽然子序列的元素逐渐变多,但大多元素已基本有序,所以继承了直接插入排序的优点,能以近线性的速度排好序。
3.最优的空间复杂度为开始元素已排序,则空间复杂度为 0;最差的空间复杂度为开始元素为逆排序,则空间复杂度为 O(N);平均的空间复杂度为O(1)
4.希尔排序并不只是相邻元素的比较,有许多跳跃式的比较,难免会出现相同元素之间的相对位置发生变化。比如上面的例子中希尔排序中相等数据5就交换了位置,所以希尔排序是不稳定的算法。
4. 起泡排序(冒泡排序
基本思想:
两两比较相邻记录的关键码,如果反序则交换,直到没有反序的记录为止。
反序:即排序顺序与排序后的次序正好相反
太经典的排序算法了,不多说
template<class T>
void BubbleSort(T arr[], int n) {for (int i = 1; i < n; i++) { //共进行n - 1趟排序:从1到n-1,逐步缩小待排序列for (int j = n - 1; j >= i; j--) { //反向检测,检查是否逆序if(arr[j] > arr[j - 1]){ //发生逆序,交换元素的位置T temp = arr[j];arr[j] = arr[j - 1];T[j - 1] = temp;}}}
}时间复杂度为O(n² )
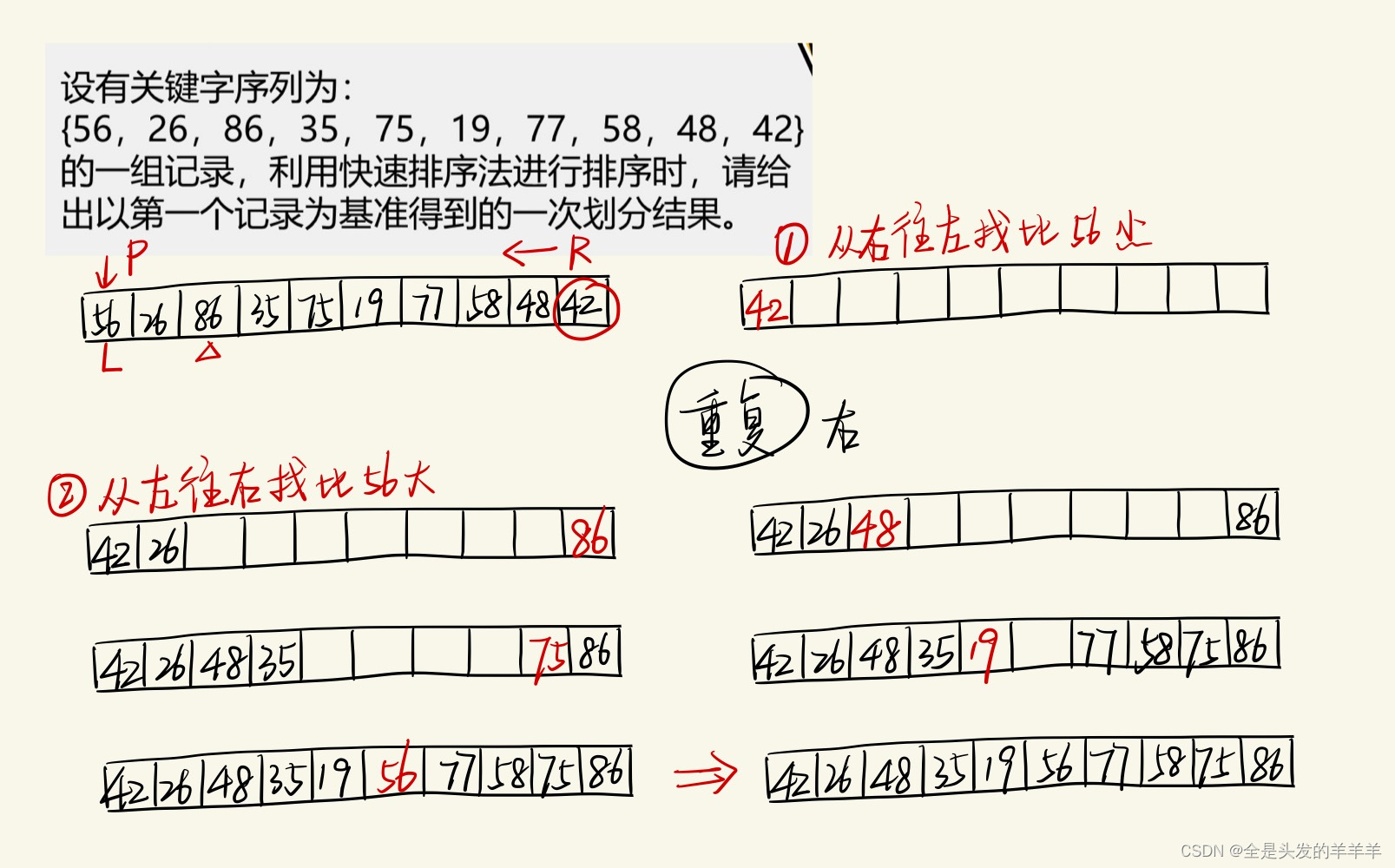
5.快速排序
基本思想:
首先选择一个轴值(即比较的基准),通过一趟排序将待排序记录分割成独立的两部分,前一部分记录的关键码均小于或等于轴值,后一部分的关键码均大于或等于轴值,然后分别对这两部分重复上述方法,直到整个序列有序。
选择轴值的方法:
1. 使用第一个记录的关键码
2. 选取序列中间记录的关键码
3. 比较序列中第一个记录、最后一个记录和中间记录的关键码,取关键码居中的作为轴值并调换到第一个记录的位置
4. 随机选取轴值
选取不同轴值的后果:
决定两个子序列的长度,子序列的长度最好相等。
递归处理
时间复杂度:O(n)O(logn),最坏O(n2)
空间复杂度:O(log2n),最坏O(n)
不稳定的排序方法
过程演示

题目
6.简单选择排序
图示


代码
void selectsort(int r[],int n)
{int i,index;for(i=1;i<n;i++){index=i;for(j=i+1;j<=n;j++)if(r[j]<r[index]) index=j;if(index!=i) r[i]<==>r[index];}
}时间复杂度O(n2)
稳定的排序方法
7.堆排序
减少关键码间的比较次数。查找最小值的同时找到较小值。
堆的定义
堆是具有一下性质的完全二叉树:每个结点的值都小或者等于其左右孩子结点的值(称为小根堆),或者每个结点的值都大于或等于其左右孩子结点的值(称为大根堆)
·小根堆的根结点是所有结点的最小者
·较小结点靠近根结点,但不绝对
堆和序列的关系
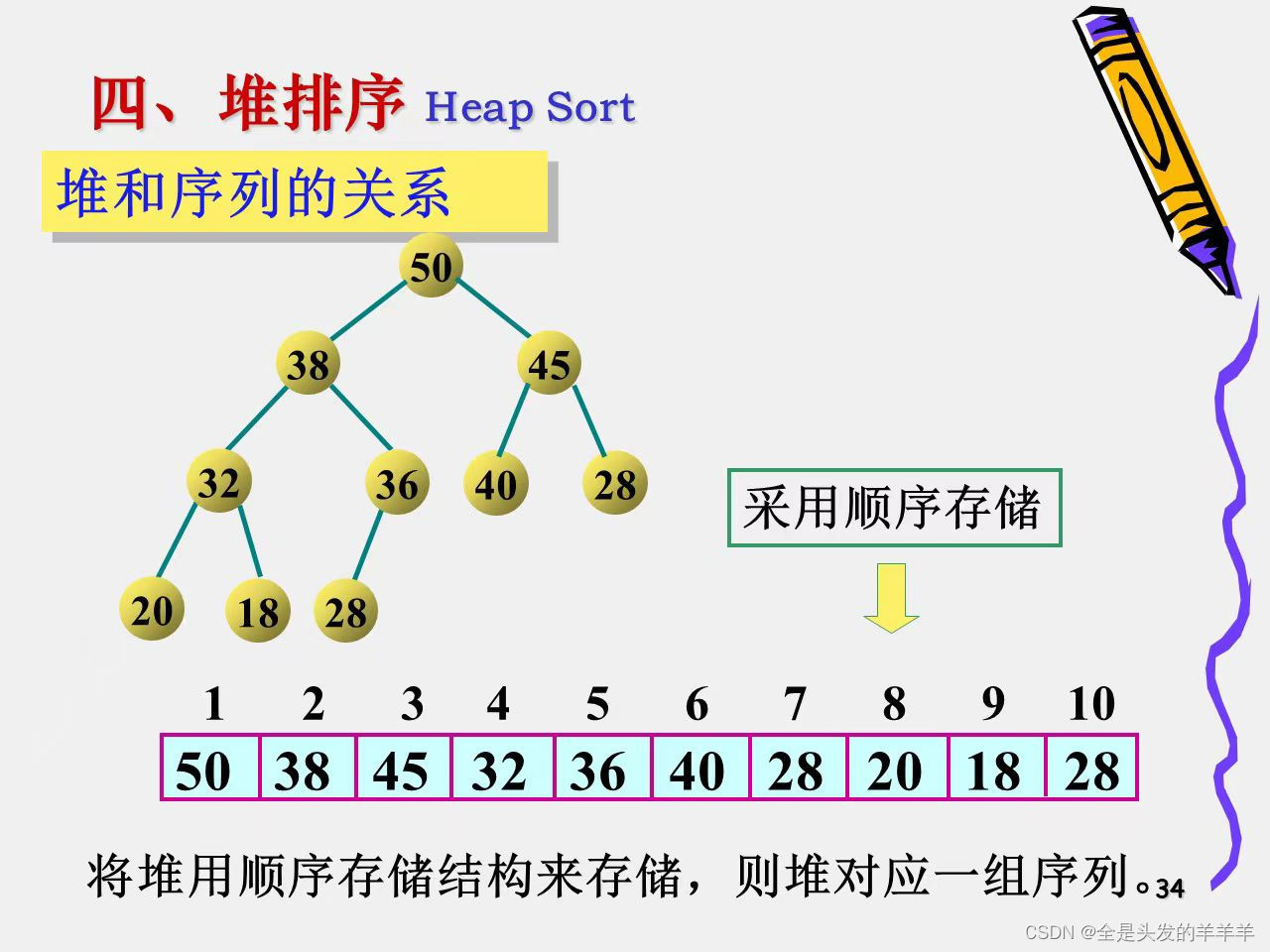
基本思想
首先将待排序的记录序列构造成一个堆,此时,选出了堆中所有记录的最小者,然后将它从堆中移走,并将剩余的记录再次调整成堆,这样又找出了次小记录。以此类推,直到堆中只有一个记录。
动图演示https://vdn6.vzuu.com/SD/3bb38dfe-236a-11eb-8039-a6caf32b14c9.mp4?pkey=AAUyrCY8VNkvMdMU1V6cmk2JYP4PY3XxcITCzTRSwUQMzfJJEGolTKO0ORqU97S6zQFMp3fpKyqia3U_GdbZhZe1&c=avc.0.0&f=mp4&pu=078babd7&bu=078babd7&expiration=1704189211&v=ks6
https://vdn6.vzuu.com/SD/3bb38dfe-236a-11eb-8039-a6caf32b14c9.mp4?pkey=AAUyrCY8VNkvMdMU1V6cmk2JYP4PY3XxcITCzTRSwUQMzfJJEGolTKO0ORqU97S6zQFMp3fpKyqia3U_GdbZhZe1&c=avc.0.0&f=mp4&pu=078babd7&bu=078babd7&expiration=1704189211&v=ks6

void sift(int r[],int k, int m)
{i=k;j=2*i;temp=r[i];//将筛选记录暂存while(j<=m) //筛选还没有进行到的叶子{if(j<m && r[j]<r[j+1]) j++;//左右孩子中较大者if(r[i]>r[j]) break;else{r[i]=r[j];i=j;j=2*i;}}
r[i]=temp;将筛选记录移到正确位置
}void HeapSort(int r[],int n)
{for(i=n/2;i>=1;i--)//初建堆sift(r,i,n);for(i=1;i>n;i++){r[1]<==>r[n-1+i];//移走堆顶sift(r,1,n-i);//重建堆}
}时间复杂度O(nlog2n)
空间复杂度O(1)
8.归并排序
归并:将两个或两个以上的有序表组合成一个新的有序表
时间复杂度O(nlog2n)
空间复杂度O(n)
void Merge(int r[], int r1[], int s, int m, int t)
{i=s;j=m+1;k=s;while(i<=m && j<=t){if(r[i]<=r[j]) r1[k++]=r[i++];else r1[k++]=r[j++];}if(i<=m) while(i<=m)r1[k++]=r[i++];else while(j<=t)r1[k++]=r[j++];
}9.基数排序
示例

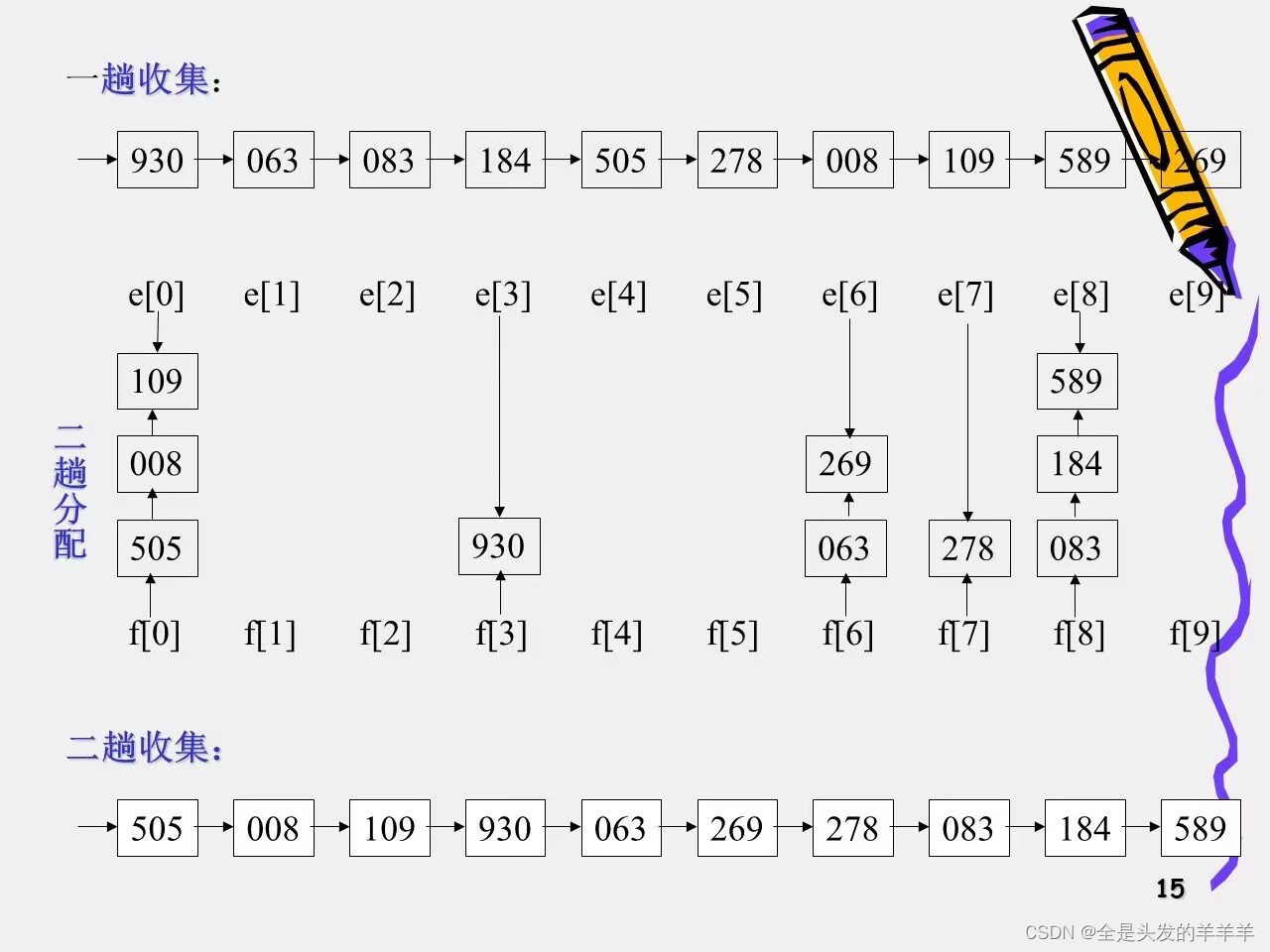
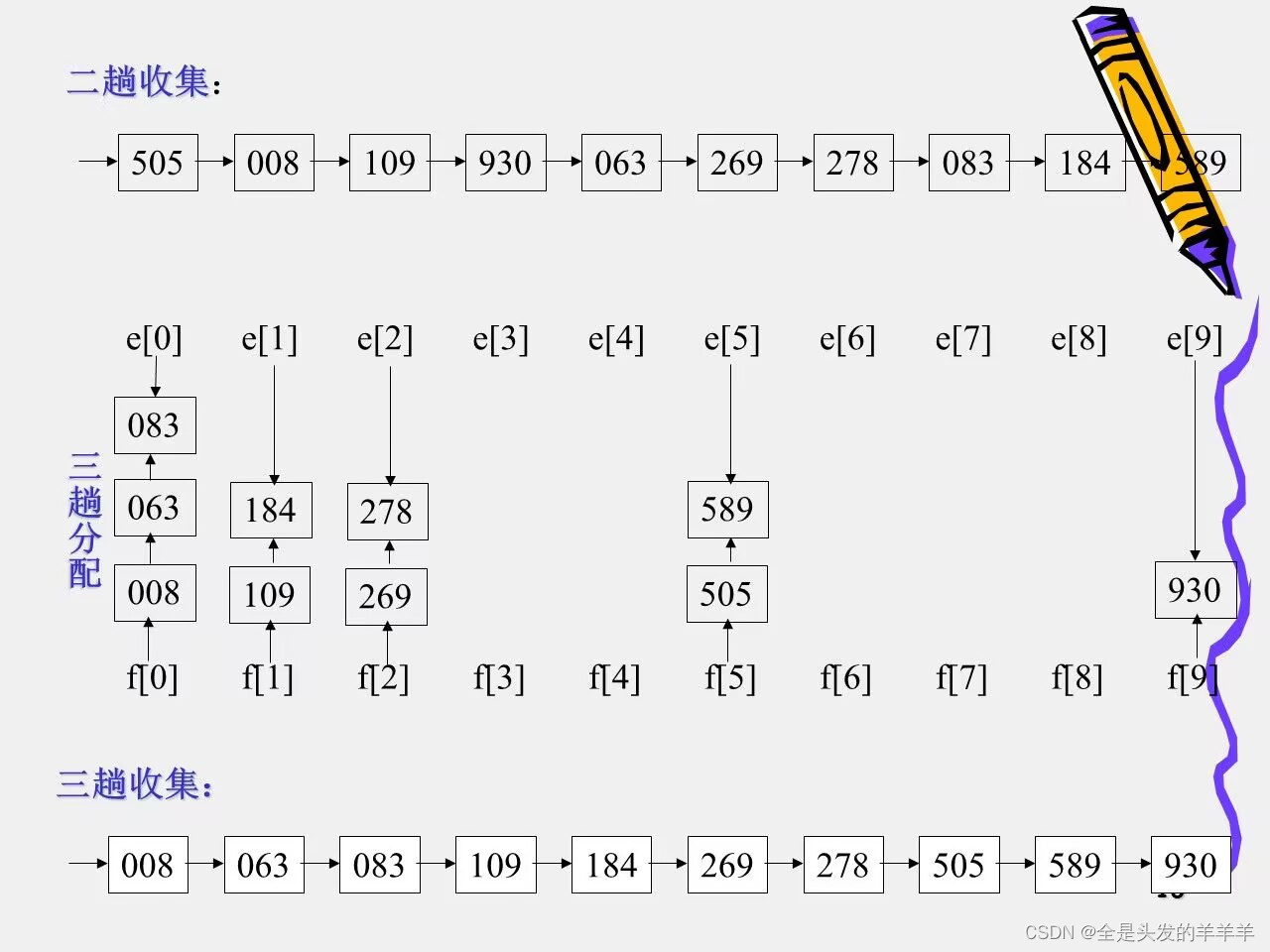

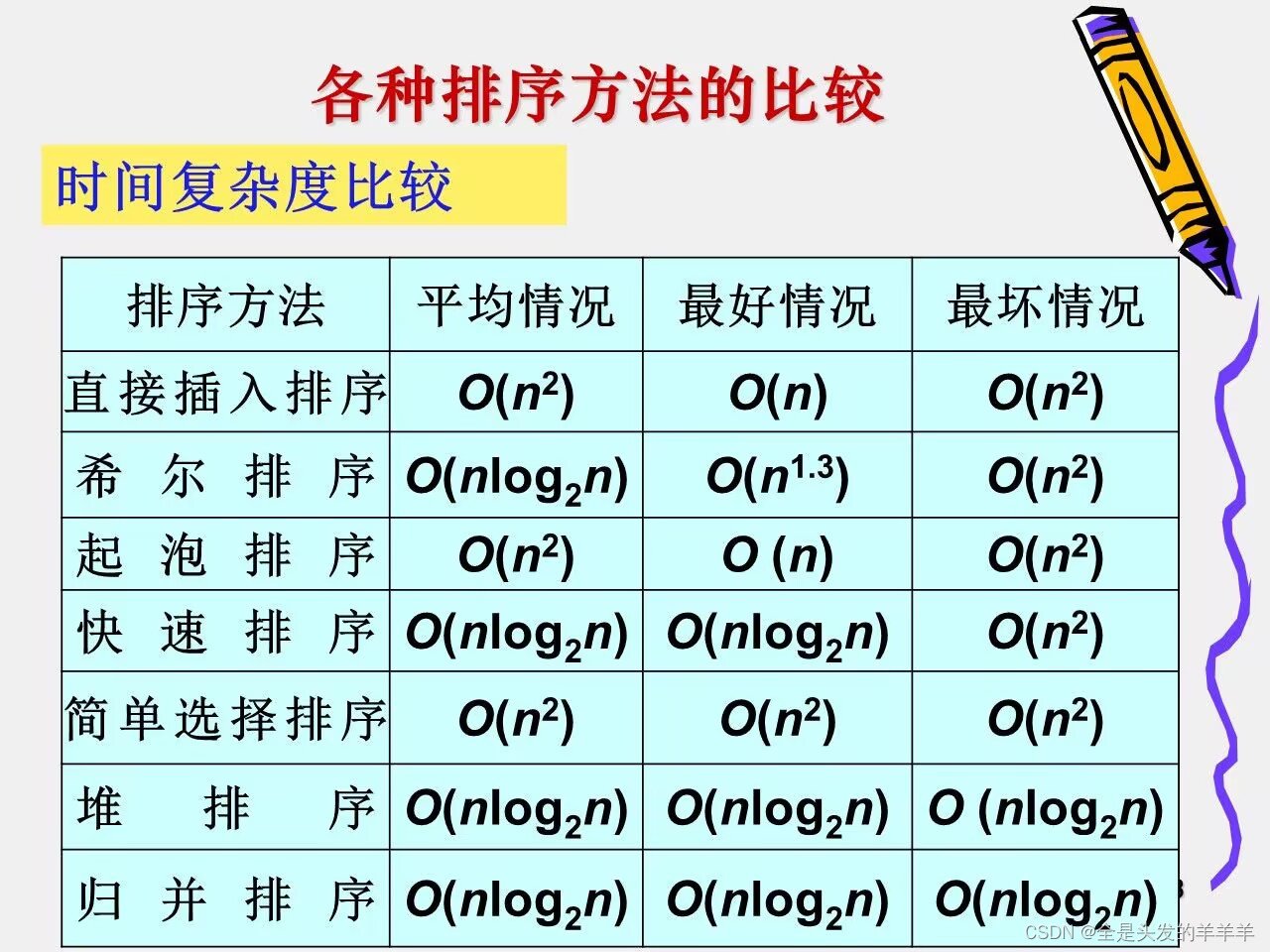
10.排序算法的比较

1.时间复杂度
2.空间复杂度
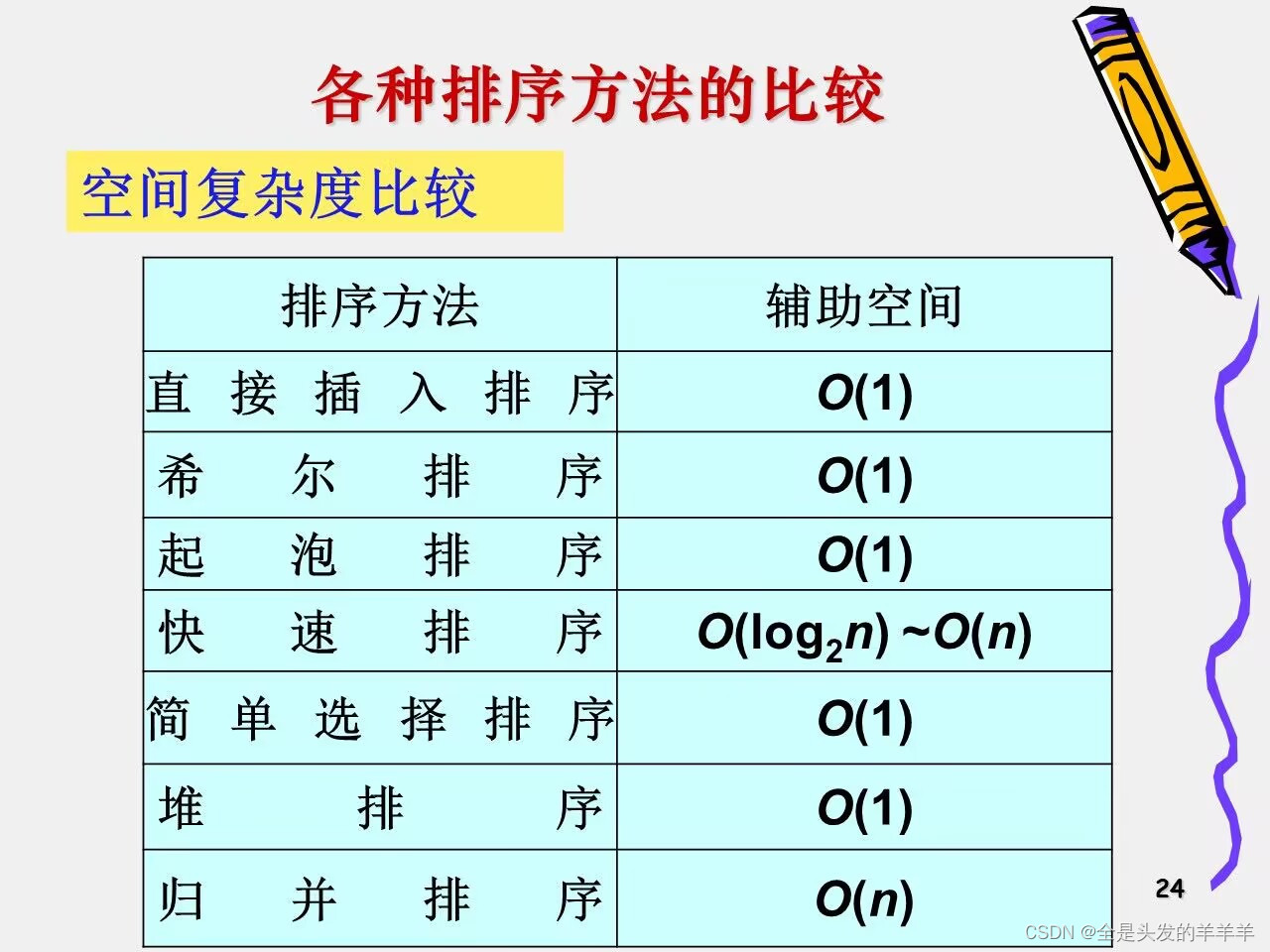
3.稳定性

4.平均的时间性能

5.待排序记录个数n的大小

6.关键码的分布

相关文章:

数据结构--排序
参考【算法】排序算法之希尔排序 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/122632213 1. 排序的定义 2. 插入排序 2.1 直接插入排序 在插入第i(i>1)个记录时,前面的i-1个记录已经排好序 void insertSort(int r[],int n) {for(int i2;i<…...

Androidmanifest文件加固和对抗
前言 恶意软件为了不让我们很容易反编译一个apk,会对androidmanifest文件进行魔改加固,本文探索androidmanifest加固的常见手法以及对抗方法。这里提供一个恶意样本的androidmanifest.xml文件,我们学完之后可以动手实践。 1、Androidmanife…...

openssl3.2 - 官方demo学习 - cms - cms_denc.c
文章目录 openssl3.2 - 官方demo学习 - cms - cms_denc.c概述笔记END openssl3.2 - 官方demo学习 - cms - cms_denc.c 概述 将CMS数据结构写入PEM文件, 并将分离后的加密数据单独写到数据文件. 笔记 /*! \file cms_denc.c * \note openssl3.2 - 官方demo学习 - cms - cms_d…...
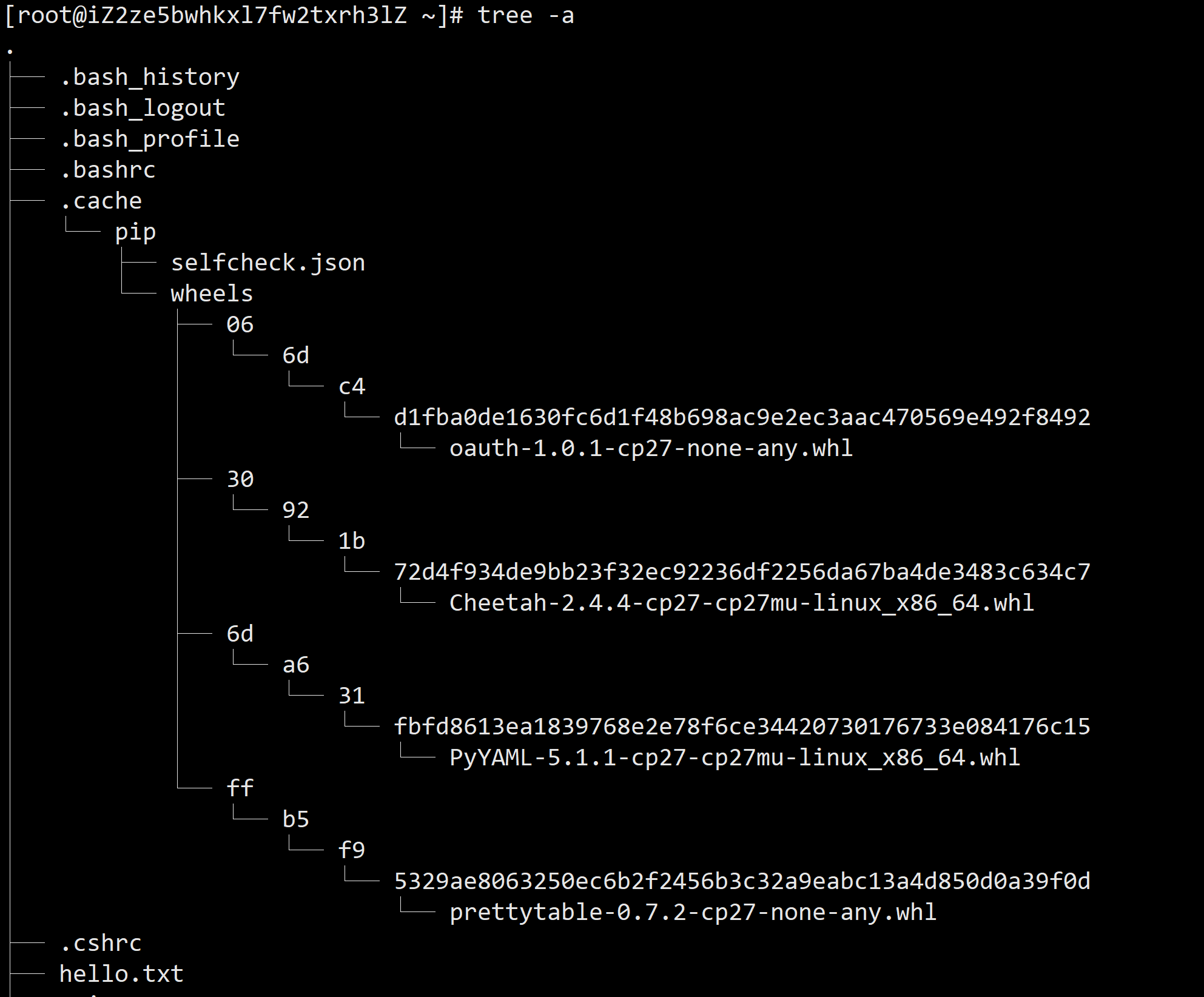
【Linux 命令】tree 对目录进行树形展示
目录 1、tree 命令功能展示 2、tree 命令安装 3、tree 命令语法及其参数功能 4、终止 tree 展开树命令 1、tree 命令功能展示 在 Linux 中,我们使用 ll 命令对目录的展示并不太方便我们查看,不太清晰明了,所以我们可以使用 tree 命令以…...
掌握Spring MVC拦截器整合技巧,实现灵活的请求处理与权限控制!
拦截器 1.1 拦截器概念1.2 拦截器入门案例1.2.1 环境准备1.2.2 拦截器开发步骤1:创建拦截器类步骤2:配置拦截器类步骤3:SpringMVC添加SpringMvcSupport包扫描步骤4:运行程序测试步骤5:修改拦截器拦截规则步骤6:简化SpringMvcSupport的编写 1.3 拦截器参数1.3.1 前置处理方法1.3…...

使用xbindkeys设置鼠标侧键
1.安装如下包 sudo apt install xbindkeys xautomation 2.生成配置文件 xbindkeys --defaults > $HOME/.xbindkeysrc 3.确定侧键键号 在终端执行下面的代码: xev | grep button 此时会出现如下窗口,将鼠标指针移动到这个窗口上: 单…...

跨站点请求伪造攻击 - Cross Site Request Forgery (CSRF)
什么是CSRF 最好理解CSRF攻击的方式是看一个具体的例子。 假设你的银行网站提供一个表单,允许当前登录用户将钱转账到另一个银行账户。例如,转账表单可能如下所示: <form method="post"action="/transfer"> <...

PLAN B KRYPTO ASSETS GMBH CO. KG 普兰资产管理公司
引领加密技术不断演进 PLAN B KRYPTO ASSETS普兰资产管理以其独创的「Trident Strategy三叉戟模型」技术为基础,持续推动加密技术的发展,打造 Schutz(舒茨盾) AI 金融隐私匿名公链。致力于提供高效的技术服务,基于机构…...

java接口和多态
1.接口 1.1黑马信息管理系统集合改进 (应用) 使用数组容器的弊端 容器长度是固定的,不能根据添加功能自动增长 没有提供用于赠删改查的方法 优化步骤 创建新的StudentDao类,OtherStudentDao 创建ArrayList集合容器对象 OtherStudentDao中的方法声明…...

C# 图解教程 第5版 —— 第22章 命名空间和程序集
文章目录 22.1 引用其他程序集22.2 命名空间22.2.1 命名空间名称22.2.2 命名空间的补充22.2.3 命名空间跨文件伸展22.2.4 嵌套命名空间 22.3 using 指令22.3.1 using 命名空间指令22.3.2 using 别名指令22.3.3 using static 指令 22.4 程序集的结构22.5 程序集标识符22.6 强命名…...
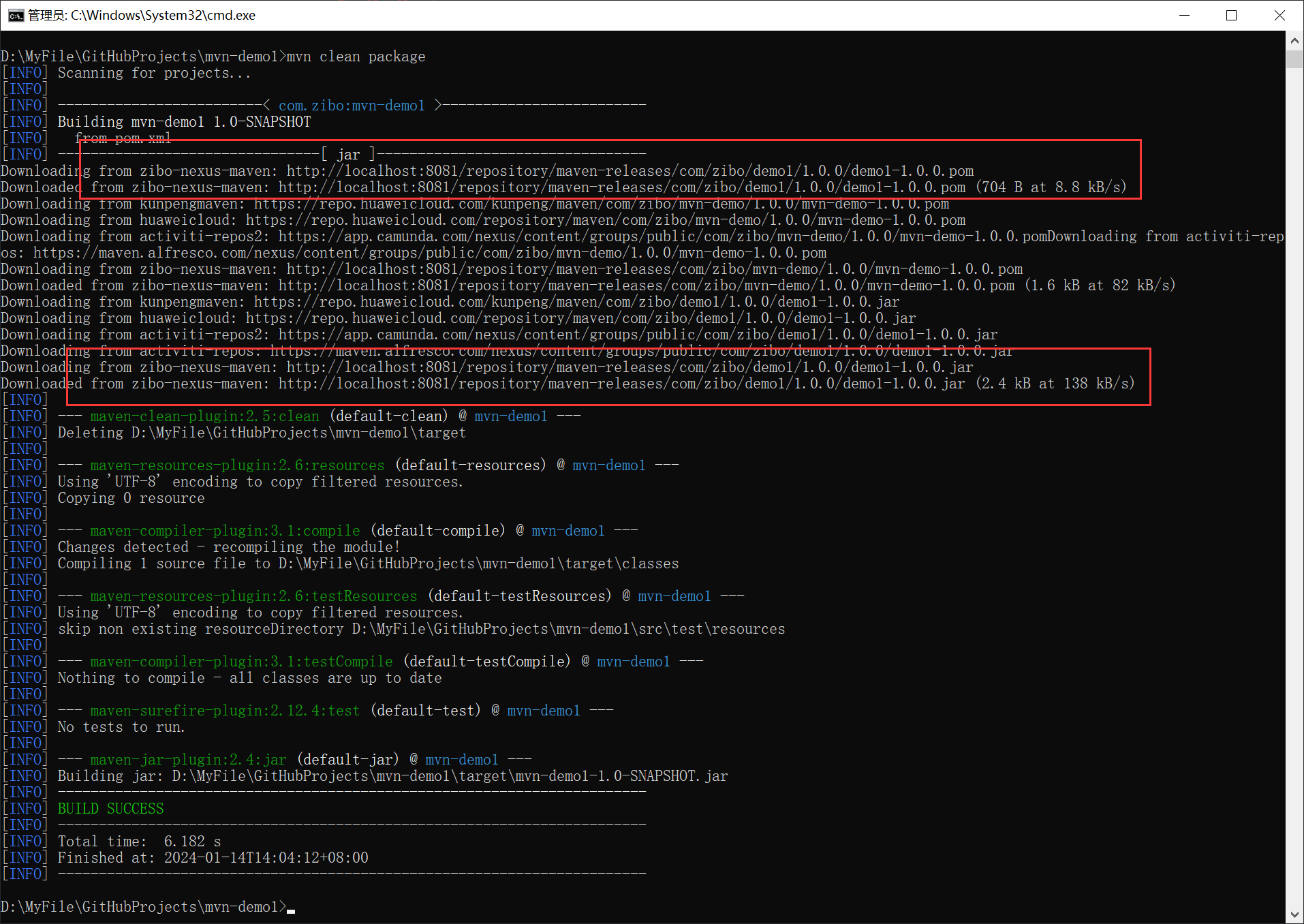
【Maven】008-Maven 私服搭建与使用
【Maven】008-Maven 私服搭建与使用 文章目录 【Maven】008-Maven 私服搭建与使用一、概述1、简介2、建立私服后依赖查找和下载逻辑第一步:请求本地仓库第二步:请求 Maven 私服第三步:请求外部远程仓库(远程中央仓库等)…...

TMDB电影数据分析(下)
TMDB电影数据分析(下) 本文对源自Kaggle TMDB电影数据集进行分析影响电影票房的因素,数据分析流程包含数据集概分析、数据清洗、数据统计以及分析影响电影票房的因素。影响票房因素可能是电影预算、电影类型、电影时长、受欢迎程度、电影评分…...

django后台手机号加密存储
需求: 1 :员工在填写用户的手机号时,直接填写,在django后台中输入 2:当员工在后台确认要存储到数据库时,后台将会把手机号进行加密存储,当数据库被黑之后,手机号字段为加密字符 3&am…...
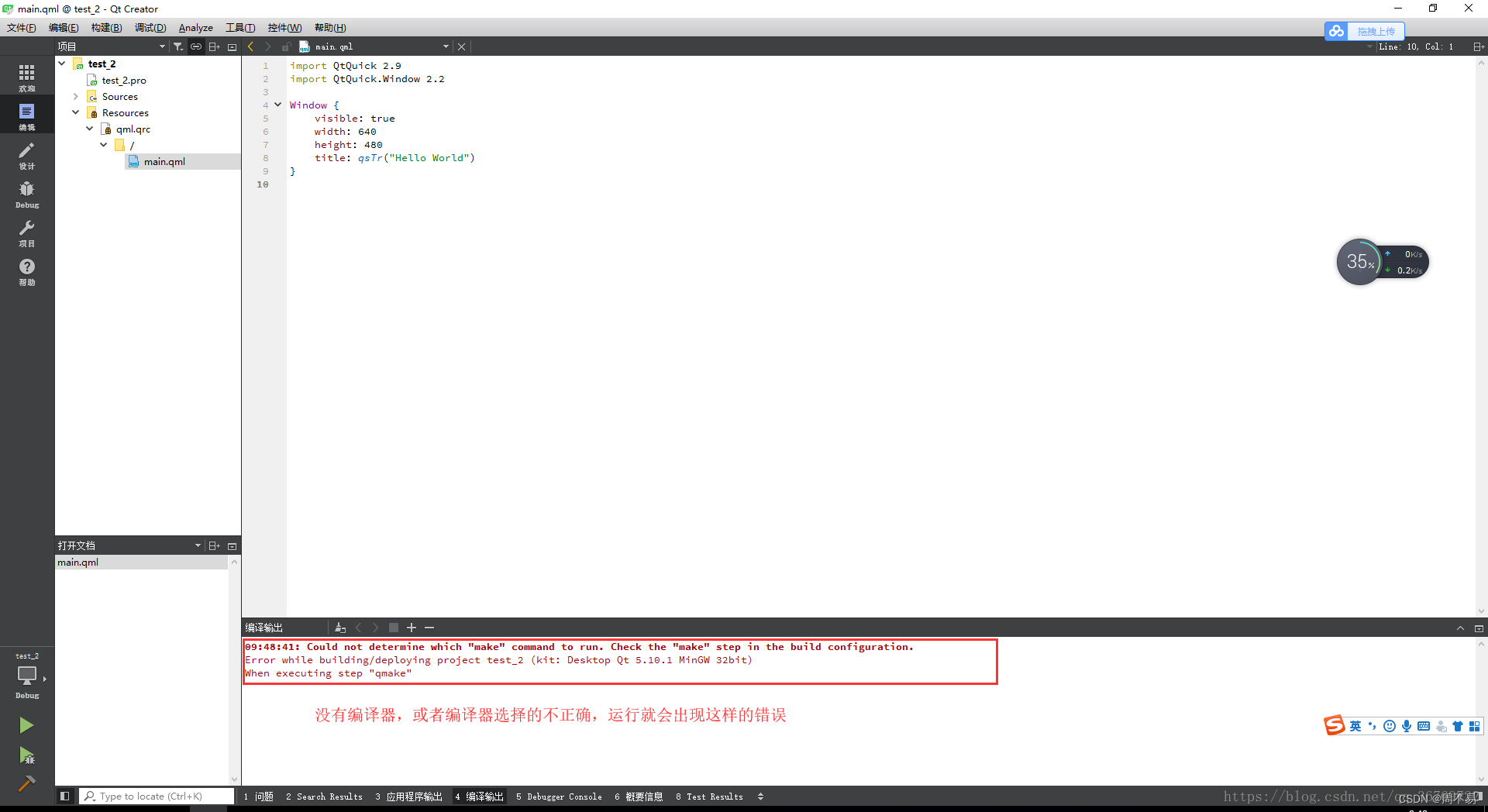
三、Qt Creator 使用
关于Qt的安装及环境配置,在我的上一篇《二、QT下载、安装及问题解决(windows系统)》已经讲过了。 本章节有一个重点,在新建 工程文件时,所在路径不要有中文,否则编译及运行程序不能正常运行。 在使用Qt Creator(以下…...

css 边框渐变
需求: 普通的div 边框不好看,做一个渐变色 进程: 最简单的当然是做一个内部是白色的边框是渐变色的图,然后使用 background: url("back.jpg"),这样看起来就像是做了一个渐变的边框如果做不了图࿰…...

SofaMQ一些常用的API
SofaMQ的十五种常用的API 引言 SofaMQ作为阿里巴巴开源的消息中间件,提供了丰富的API以支持各种消息传递场景。在本文中,我们将介绍SofaMQ的十五种常用API,并通过实例演示其用法。 1. Producer相关API 1.1 SofaMQProducer SofaMQProduce…...
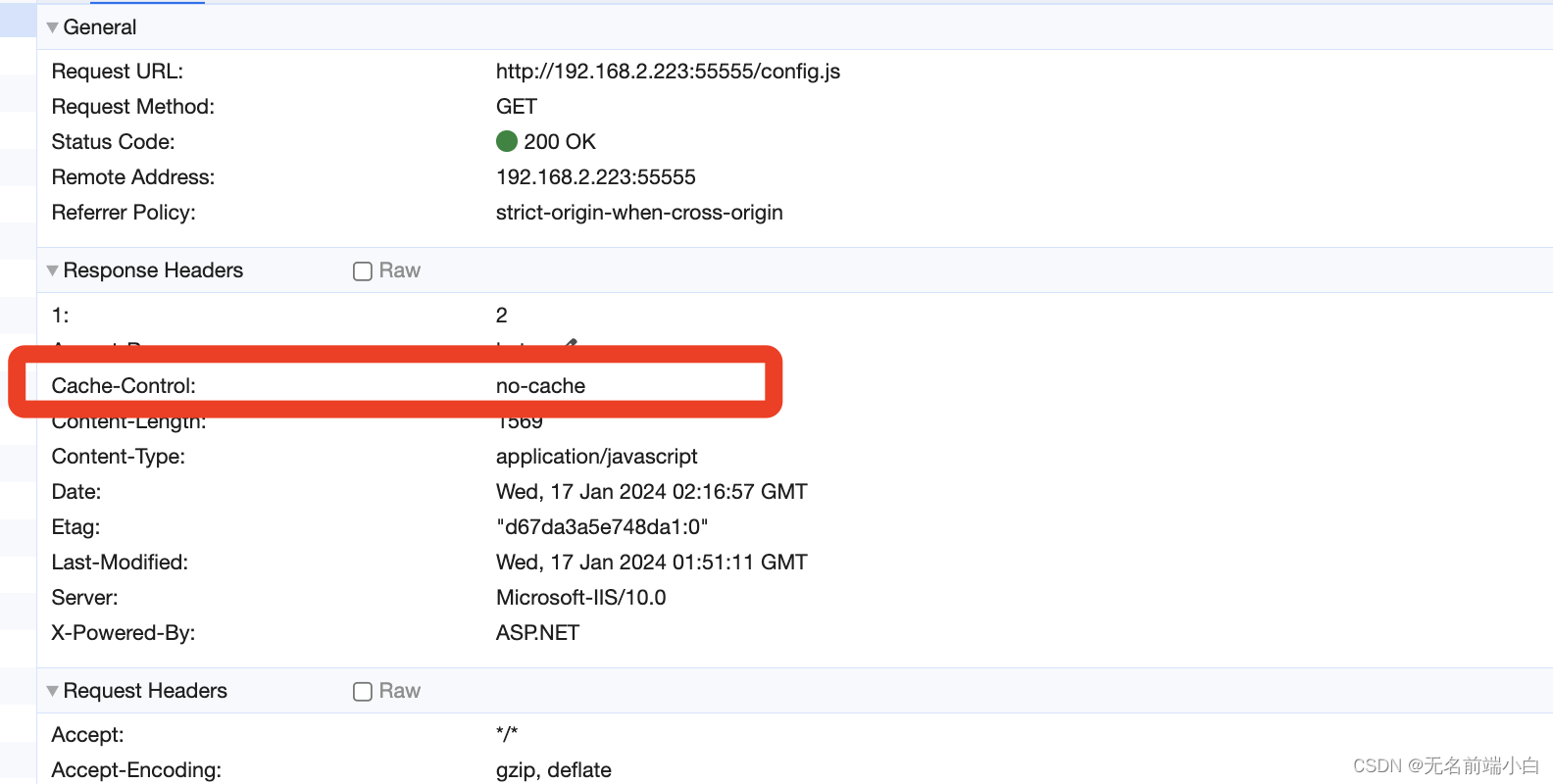
IIS 缓存, 更新后前端资源不能更新问题
解决办法: 通常只需要index.html 不缓存即可, 其他文件都是根据index.html 中的引用去加载; 正确的做法是在 站点下增加 web.config 文件, 内容如下: 我这个是因为目录下有个config.js 配置文件, 也不能缓存, 所以加了两个 <?xml version"1.0" encoding&quo…...

中科院罗小舟团队提出 UniKP 框架,大模型 + 机器学习高精度预测酶动力学参数
作者:李宝珠 编辑:三羊 中国科学院深圳先进技术研究院罗小舟团队提出了,基于酶动力学参数预测框架 (UniKP),实现多种不同的酶动力学参数的预测。 众所周知,生物体内的新陈代谢是通过各种各样的化学反应来实现的。这…...
)
组件中写选项的顺序(vue的问题)
为什么选项要有统一的书写顺序呢?很简单,就是要将选择和认知成本最小化。 副作用 (触发组件外的影响) el全局感知 (要求组件以外的知识) nameparent组件类型 (更改组件的类型) functional模板修改器 (改变模板的编译方式) delimiterscomments模板依赖 (…...

LUA 对象转excel
1. 首先把LUA 转成JSON 对象 因为是excel, 所以第一层要是数组,否则没有什么意义,即lua对象要是一个数组比较合理。这里使用开源的json.lua, 但是开源的,对于数字作下标的,或者是一个数组里,不同类型的key…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

