2018年认证杯SPSSPRO杯数学建模D题(第一阶段)投篮的最佳出手点全过程文档及程序
2018年认证杯SPSSPRO杯数学建模
对于投篮最佳出手点的探究
D题 投篮的最佳出手点
原题再现:
影响投篮命中率的因素不仅仅有出手角度、球感、出手速度,还有出手点的选择。规范的投篮动作包含两膝微屈、重心落在两脚掌上、下肢蹬地发力、身体随之向前上方伸展、同时抬肘向投篮方向小臂推而伸出、手腕下压、手指弹射,这样能够将脚趾力量完全连贯到手指,这种下肢、手臂、手腕、手指头都充分用到力量的投篮,看起来很柔顺、优美,具有艺术性,命中率高。但是身材相对矮小的组织后卫,如果采用这种规范的投篮动作,势必出手时间较长,给防守者以充分的时间做准备,被盖帽的可能性增大。反之,如果出手点较低,可以缩短从开始发力到篮球出手的时间,防止被盖帽,但是手臂、手腕以及手指头的力量可能没有被完全使上,必然使得篮球旋转不够,篮球飞行轨迹偏移较大,另外碰到篮筐、篮板后的反弹进球概率也大大降低。某 NBA 球队的技术顾问希望你的团队能帮助他们提高组织后卫在高强度防守下的投篮命中率。
第一阶段问题:
1. 假定该后卫的身高是 1.91m,垂直弹跳 30 英寸,助跑弹跳 34 英寸,跳起摸高达到 3.40m,请建立数学模型,为该后卫推荐一个最佳的出手点。
2. 如果要选择打板进球(利用篮板进球可以选择一些比较特殊的出手角度,往往能够骗过防守球员,使得投篮者获得更多的出手时间),上面一问中的最佳出手点模型该如何作出调整?
整体求解过程概述(摘要)
本文主要针对球员投篮时出手点的高度与球出手的时间、出手角度、以及出手时发力的关系,考虑到了防守时的一些约束条件,还有对于打板投篮问题的深入思考与分析。在探究过程中,本组查找并且观察、分析了一些NBA球员的比赛录像,搜索了部分身体各项数据与问题所给出的数据相似的NBA球员,记录下他们的有关数值,进行平均值的求解或者其他研究项目。同时,很好地运用了场地条件,进行各个猜想的实践验证,通过慢动作的回放以及对于动作或球路的解析,将其与理论结合,成为自己研究的成果。
具体分析:
在问题1中,根据问题的描述,我组考虑到了出手时的一些数据,主要是出手时的高度。我们通过建立二维函数、三角函数模型得到了出手点高度与出手时间的关系,通过拟合建立三角函数模型,线条模型,可以得到出手点高度与出手角度的关系。
通过模拟刚体模型,运用物理中转动惯量、能量、曲线运动的知识,探究出了出手点高度与球的旋转的关系。
最后引入了球员发力舒适度这一个量,查阅网络资料,了解了关于人体比例的关系,但因为较难将其定量,因此得到了大致的结论。之后我们转变方向,利用肌肉收缩的能量消耗和时间以及出手点高度建立关系,从而得到了关于在不同出手点球员对出手力量的感觉的关系。
之后我们从防守队员的角度来探究,通过查阅网络资料,编程求值,以及进行合理的假设,可以得出防守球员的一些有关数值,然后将其带入进攻球员的投篮过程之中,考虑“高强度防守”,一步步地深入,接近现实情况,将球员的出手点与防守结合考虑,最终得到比较而言的最佳出手点。
在第2问中,首先假设了较为理想的状况,将篮球打板的过程分为三个阶段。
第一阶段用斜抛运动的模型,分析并得出了球与篮板碰撞的位置距离地面的高度。
第二阶段,利用完全弹性碰撞模型,运用动能知识,得到了碰撞反弹后与竖直平面的夹角。
在第三阶段,建立了碰撞后球的行进路线的模型,最终重新得到了打板投篮时出手点高度与其它变量的大致关系。将三个阶段的模型相结合,最后可以得出调整后的最佳出手点。
问题分析:
本道题主要研究在篮球比赛中投篮的问题,需要我们具有一定的篮球运动方面的知识,并且对于规则有一定的了解,对于篮球运动员的身体素质,身高,以及对手的各项数据与能力,还需要包括考虑许多自然的因素综合考虑,得出最佳的方案。
模型假设:
1.在所有模型中都忽略空气阻力的影响
2.先建立的四种模型中都先不考虑防守队员的因素,在最后对防守队员进行分析后作为约束条件加入前四种模型
3.篮球出手速度和人在投篮时的初速度都是一个常量
4.在第三种模型中忽略内能和质量的变化
5.将球与篮板的碰撞视为完全弹性碰撞
6.在第一、二种情况中,投篮时身体向上和抬起大臂同时开始、同时结束;在第三、四种情况中,双脚离地之前投篮准备动作已经完成。
论文缩略图:

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
clc
r=[1:0.1:8];
y=atan((0.83*r.^2-0.4)./(r.^2-r));
y1=atan((0.73*r.^2-0.4)./(r.^2-r));
y2=atan((0.63*r.^2-0.4)./(r.^2-r));
y3=atan((0.53*r.^2-0.4)./(r.^2-r));
A=y.*180/pi;B=y1.*180/pi;C=y2.*180/pi;D=y3.*180/pi
plot(r,A,r,B,r,C,r,D);
r=[1.6:0.1:8]
a=atan((0.83*r.^2-0.4)./(r.^2-r));
v0=(9.8*r.^2./(r.*sin(2*a)-0.8*cos(a).*cos(a))).^(1/2)
a=atan((0.73*r.^2-0.4)./(r.^2-r));
v1=(9.8*r.^2./(r.*sin(2*a)-0.8*cos(a).*cos(a))).^(1/2)
a=atan((0.63*r.^2-0.4)./(r.^2-r));
v2=(9.8*r.^2./(r.*sin(2*a)-0.8*cos(a).*cos(a))).^(1/2)
a=atan((0.53*r.^2-0.4)./(r.^2-r));
v3=(9.8*r.^2./(r.*sin(2*a)-0.8*cos(a).*cos(a))).^(1/2)
plot(r,v0,'r',r,v1,'b',r,v2,'y',r,v3)
r=[1:0.1:8];
y=atan((0.83*r.^2-0.4)./(r.^2-r));
y1=atan((0.73*r.^2-0.4)./(r.^2-r));
y2=atan((0.63*r.^2-0.4)./(r.^2-r));
y3=atan((0.53*r.^2-0.4)./(r.^2-r));
A=y.*180/pi;B=y1.*180/pi;C=y2.*180/pi;D=y3.*180/pi
plot(r,A,r,B,r,C,r,D);
r=[1:0.1:8]
detah=r.^(-2)-0.8*r.^(-3)
plot(r,detah)
r=[1:0.1:8]
h=0.4*r.^(-2)-2.61*r.^(-1)+2.15;
plot(r,h)
n=1+r.^(-1)-0.4*r.^(-2)
plot(r,n,r,h)
r=[1:0.1:8];
y=atan((0.83*r.^2-0.4)./(0.8*(r.^2-r)))
E=y.*180/pi
y=atan((0.83*r.^2-0.4)./((r.^2-r)))
F=y.*180/pi
y=atan((0.83*r.^2-0.4)./(1.2*(r.^2-r)))
G=y.*180/pi
plot(r,E,'r',r,F,'g',r,G,'b')
r=[1:0.1:8]
h=0.4*r.^(-2)-2.61*r.^(-1)+2.15;
plot(r,h)
n=1+r.^(-1)-0.6*r.^(-2)
plot(r,n,r,h)
r=[1:0.1:8]
h1=(r.*(r-1)*0.7+0.4).*r.^(-2)
h2=(r.*(r-1)+0.4).*r.^(-2)
h3=(r.*(r-1)*1.2+0.4).*r.^(-2)
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2018年认证杯SPSSPRO杯数学建模D题(第一阶段)投篮的最佳出手点全过程文档及程序
2018年认证杯SPSSPRO杯数学建模 对于投篮最佳出手点的探究 D题 投篮的最佳出手点 原题再现: 影响投篮命中率的因素不仅仅有出手角度、球感、出手速度,还有出手点的选择。规范的投篮动作包含两膝微屈、重心落在两脚掌上、下肢蹬地发力、身体随之向前上…...
使用pdfbox 为 PDF 增加水印
使用pdfbox 为 PDF增加水印https://www.jylt.cc/#/detail?activityIndex2&idbd410851b0a72dad3105f9d50787f914 引入依赖 <dependency><groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>3.0.1</ve…...

6.【CPP】Date类的实现
Date.h #pragma once using namespace std; #include<iostream>class Date {friend ostream& operator<<(ostream& out, const Date& d);friend istream& operator>>(istream& in, Date& d); public://构造函数会被频繁调用,放在类…...
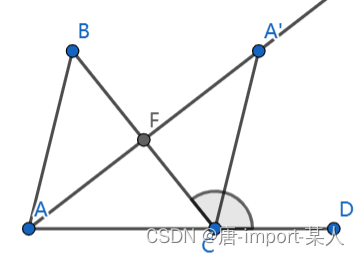
三角形任意一外角大于不相邻的任意一内角
一.代数证明 ∵ 对与△ A C B 中 ∠ c 外接三角形是 ∠ B C D ∵对与△ACB中∠c外接三角形是∠BCD ∵对与△ACB中∠c外接三角形是∠BCD ∴ ∠ B C D π − ∠ C ∴∠BCD\pi-∠C ∴∠BCDπ−∠C ∵ ∠ A ∠ B ∠ C π ∵∠A∠B∠C\pi ∵∠A∠B∠Cπ ∴ ∠ B C D ∠ A ∠…...

【Spring Boot 3】【Redis】集成Lettuce
【Spring Boot 3】【Redis】集成Lettuce 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是要花…...
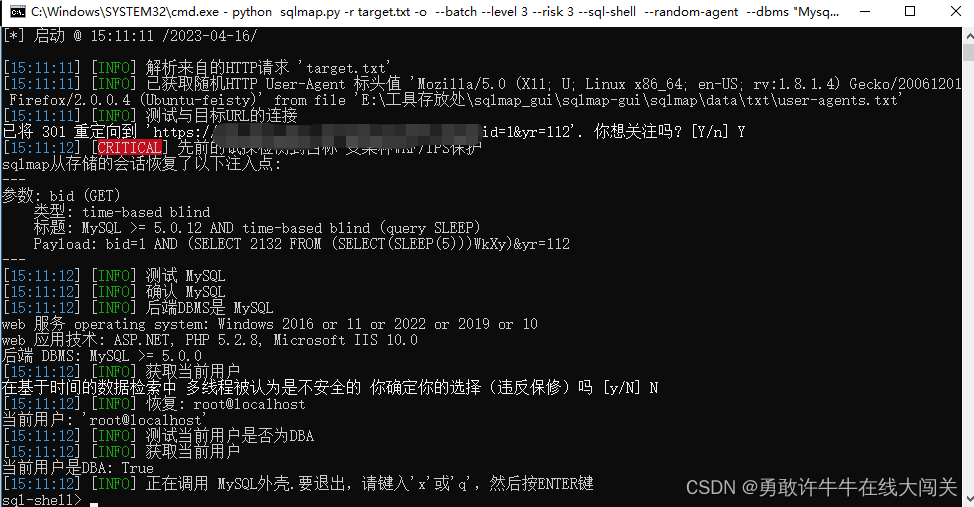
【SQL注入】SQLMAP v1.7.11.1 汉化版
下载链接 【SQL注入】SQLMAP v1.7.11.1 汉化版 简介 SQLMAP是一款开源的自动化SQL注入工具,用于扫描和利用Web应用程序中的SQL注入漏洞。它在安全测试领域被广泛应用,可用于检测和利用SQL注入漏洞,以验证应用程序的安全性。 SQL注入是一种…...
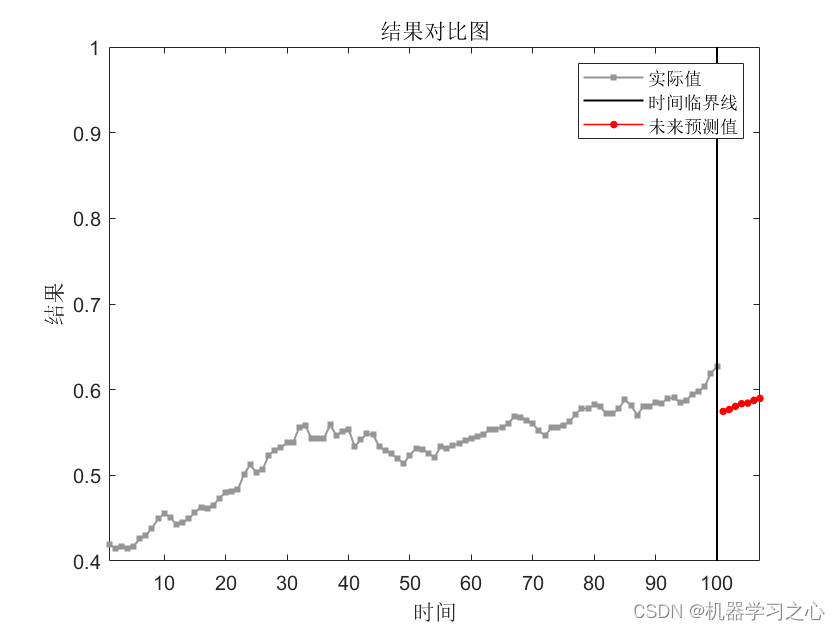
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤)
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤) 目录 时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤)预测效果基本介绍程序设计参考资料预测效果 基本介绍 MATLAB实现GRNN广义回归神经网络时间序列…...

长期戴耳机的危害有哪些?戴哪种耳机不伤耳朵听力?
长期佩戴耳机可能会出现听力下降、耳道感染等危害。 听力下降:长时间戴耳机可能会导致耳道内的声音过大,容易对耳膜造成一定的刺激,容易出现听力下降的情况。 耳道感染:长时间戴耳机,耳道长期处于封闭潮湿的情况下&a…...

C++中的预处理
一.预定义符号 1.__FILE__进行编译的源文件 2.__LINE__文件当前的行号 3.__DATE__文件被编译的日期 4.__TIME文件被编译的时间 5.__STDC__如果编译器遵循ANSIC,其值为1,否则未定义 二.#define 基本语法:#define 名字 内容 eg.define M 1 经#define定义的常量时不经过…...
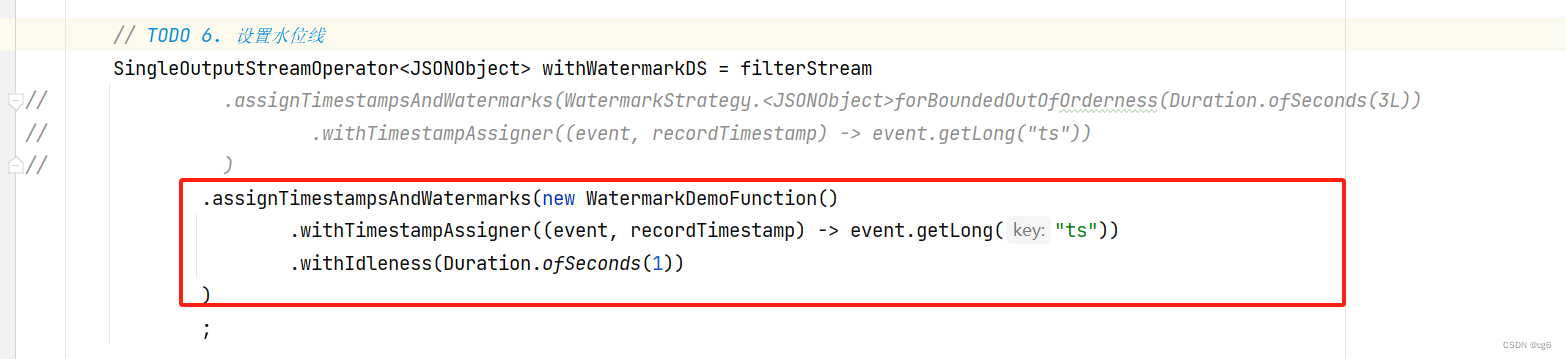
flink 最后一个窗口一直没有新数据,窗口不关闭问题
flink 最后一个窗口一直没有新数据,窗口不关闭问题 自定义实现 WatermarkStrategy接口 自定义实现 WatermarkStrategy接口 窗口类型:滚动窗口 代码: public static class WatermarkDemoFunction implements WatermarkStrategy<JSONObject…...

mybatis----小细节
1、起别名 在MyBatis中,<typeAliases>元素用于定义类型别名,它可以将Java类名映射为一个更简短的别名,这样在映射文件中可以直接使用别名而不需要完整的类名。 下面是一个示例: 在mybatis核心配置文件中配置typeAliases标…...

解密Oracle数据库引擎:揭开数据存储的神秘面纱
目录 1、介绍Oracle数据库引擎 1.1 什么是Oracle数据库引擎 1.2 Oracle数据库引擎的作用和功能 1.3 Oracle数据库引擎的历史和发展 2、Oracle数据库引擎的体系结构 2.1 Oracle数据库实例的组成部分 2.2 Oracle数据库引擎的层次结构 2.3 Oracle数据库引擎的关键组件 3、…...

「HDLBits题解」Karnaugh Map to Circuit
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 相关资料:卡诺图化简法-CSDN博客 题目链接:Kmap1 - HDLBits module top_module(input a,input b,input c,output out );assig…...
由于找不到d3dcompiler_43.dll缺失,无法打开软件的解决方法分享
d3dcompiler43.dll是什么文件?为什么会出现丢失的情况?又该如何解决呢?本文将详细介绍d3dcompiler43.dll的作用和影响,并提供6个有效的解决方法。 一、d3dcompiler43.dll是什么文件? d3dcompiler43.dll是DirectX SDK…...
现阶段Python和Java哪个更吃香?
现阶段Python和Java哪个更吃香? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「Java的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!&…...

基于DNA的密码学和隐写术综述
摘要 本文全面调研了不同的脱氧核糖核酸(DNA)-基于密码学和隐写术技术。基于DNA的密码学是一个新兴领域,利用DNA分子的大规模并行性和巨大的存储容量来编码和解码信息。近年来,由于其相对传统密码学方法的潜在优势,如高存储容量、低错误率和对环境因素的抗性,该领域引起…...

【linux 多线程并发】多线程的控制,挂起线程暂停运行,直到唤醒线程,取消线程运行,可以设置合适的取消点属性避免不安全点被中止
线程运行控制 专栏内容: 参天引擎内核架构 本专栏一起来聊聊参天引擎内核架构,以及如何实现多机的数据库节点的多读多写,与传统主备,MPP的区别,技术难点的分析,数据元数据同步,多主节点的情况…...
java转义字符
//转义字符的使用 public class ChangeChar{//编写一个main方法public static void main(String[] args){// \t :一个制表位,实现对齐的功能System.out.println("北京\t天津\t上海");// \n :换行符,实现换行System.out.println("jack\nsm…...

UDP服务器和客户端的创建步骤
UDP服务器的创建步骤: 一、创建用户数据报套接字(socket函数):通信域选择IPV4网络协议、套接字类型选择数据报式; int sockfd socket(AF_INET,SOCK_DGRAM,0); 二、填充服务器的网络信息结构体:1.定义网络…...
【问题记录】使用命令语句从kaggle中下载数据集
从Kaggle中下载Tusimple数据集 1.服务器环境中安装kaggle 使用命令:pip install kaggle 2.复制下载API 具体命令如下: kaggle datasets download -d manideep1108/tusimple3.配置kaggle.json文件 如果直接使用命令会报错: root:~# kagg…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
