机器学习算法理论:贝叶斯
贝叶斯定理对于机器学习来说是经典的概率模型之一,它基于先验信息和数据观测来得到目标变量的后验分布。具体来说,条件概率(也称为后验概率)描述的是事件A在另一个事件B已经发生的条件下的发生概率,公式表示为P(A|B),读作“在B条件下A的概率”。
最常用的贝叶斯机器学习模型
-
朴素贝叶斯模型:这是一个基于贝叶斯定理的分类算法,其核心思想是:对于给定的输入特征,假设每个特征之间都是独立的。尽管这个假设在实际应用中可能不成立,但朴素贝叶斯模型在许多场景下都表现出了很好的性能。
-
贝叶斯网络模型:这是一个用于表示变量之间复杂关系的概率图模型。贝叶斯网络可以用于推断、学习和推理,广泛应用于各种机器学习任务中。
基本原理
公式:
其中:
:表示在B发生的情况下,A发生的概率,即得自B的取值而被称作A的后验概率
:表示在A发生的情况下,B发生的概率,即得自A的取值而被称作B的后验概率
:表示A发生的概率,也称A的先验概率
:表示B发生的概率,也称B的先验概率
例1
现分别有 A、B 两个容器,在容器 A 里分别有 7 个红球和 3 个白球,在容器 B 里有 1 个红球和 9 个白球,那么从这两个容器里任意抽出了一个红球,问这个球来自容器 A 的概率是多少?
首先我们先定义事件:
- A:为选中A容器
- B:为抽出红球
已知:
:抽中红球的概率为8/20
:选中A容器的概率1/2
:在A容器内抽中红球的概率为7/10
求:从这两个容器里任意抽出了一个红球,问这个球来自容器 A 的概率是多少?
套入公式:
解得: 从这两个容器里任意抽出了一个红球,这个球来自容器 A 的概率87.5%
例2
假设新冠状病毒测试,用于检测是否感染了新冠状病毒。这个测试不是100%准确,会有假阳性和假阴性的情况。那么,测试结果为阳性的概率(阳性率)是98%,测试结果为阴性的概率(阴性率)是95%,实际感染新冠状病毒的人的概率(患病率)是1%,现在,有一个人的测试结果为阳性,根据以上信息判断这个人是否真的感染了新冠状病毒。
| 阳性率 | 阴性率 | 患病率 |
| 98% | 95% | 1% |
首先我们先定义事件:
:测试结果为阳性
:实际感染了病毒
:未感染病毒
根据以上信息已知:
:在实际感染病毒患病的情况下,测试结果为阳性的概率,即真阳性率。这个值是98%
:在未感染病毒患病的情况下,测试结果为阳性的概率,即假阳性率。这个值是2%(100%-98%)
:实际感染病毒患病率为1%
:实际未感染新冠状病毒的概率,即99%
:测试为阳性的总概率
使用全概率公式计算:
其中,表示事件A发生的概率,
表示对所有可能的状态
求和,
表示状态
的概率,
表示在状态
下事件
发生的概率。
代入贝叶斯公式计算:
即测试结果为阳性,是否真的感染了新冠状病毒的概率
解得: 测试结果为阳性,确认感染了新冠状病毒的概率约为33%。
朴素贝叶斯
朴素贝叶斯是一种基于贝叶斯定理的分类算法,它假设特征之间相互独立。朴素贝叶斯在文本分类、垃圾邮件过滤、情感分析等领域有广泛应用。朴素贝叶斯的基本原理是:对于给定的训练数据集,计算每个类别的概率,然后根据输入的特征计算属于每个类别的概率,最后选择概率最大的类别作为预测结果。
示例
使用sklearn库的朴素贝叶斯分类器
from sklearn.datasets import fetch_openml # 导入fetch_openml函数,用于加载Fashion MNIST数据集
from sklearn.model_selection import train_test_split # 导入train_test_split函数,用于将数据集划分为训练集和测试集
from sklearn.naive_bayes import GaussianNB # 导入GaussianNB类,用于创建朴素贝叶斯分类器
from sklearn.metrics import accuracy_score # 导入accuracy_score函数,用于计算预测准确率# 加载Fashion MNIST数据集
fashion_mnist = fetch_openml('fashion_mnist', version=1)
X = fashion_mnist.data # 获取数据集的特征
y = fashion_mnist.target # 获取数据集的标签# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建朴素贝叶斯分类器
gnb = GaussianNB()# 训练模型
gnb.fit(X_train, y_train)# 预测测试集结果
y_pred = gnb.predict(X_test)# 输出预测准确率
print("朴素贝叶斯分类器预测准确率:", accuracy_score(y_test, y_pred))
相关文章:
机器学习算法理论:贝叶斯
贝叶斯定理对于机器学习来说是经典的概率模型之一,它基于先验信息和数据观测来得到目标变量的后验分布。具体来说,条件概率(也称为后验概率)描述的是事件A在另一个事件B已经发生的条件下的发生概率,公式表示为P(A|B)&a…...
】手机App防沉迷系统(模拟-JavaPythonC++JS实现))
229.【2023年华为OD机试真题(C卷)】手机App防沉迷系统(模拟-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-手机App防沉迷系统二.解题思路三.题解代码Pyth…...
关系运算符
Oracle从入门到总裁:https://blog.csdn.net/weixin_67859959/article/details/135209645 补充: 如果要想对所选择的数据行进行控制,那么可以利用 WHERE 子句完成,此时的 SQL 语法结构变为如下形式 先系统性介绍下: ● 关系运算: >、、&…...
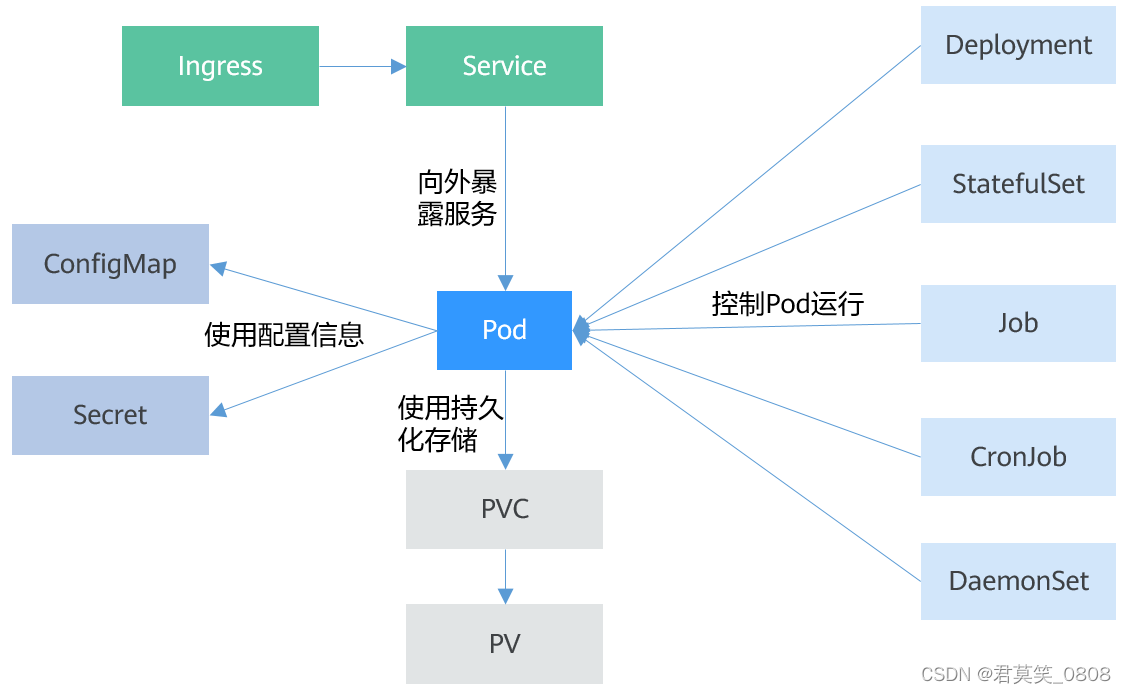
K8s-架构
一、K8s节点划分 K8s集群包含Master(控制节点)和Node(工作节点),应用部署在Node节点上。 集群架构图: 二、Master节点 Master节点分成四个组件:scheduler、ApiServer、Controller Manager、ETCD。类似三层结构,controller&#…...

C++ 并发编程 | 进程与线程
一、进程与线程 1、进程 1.1、定义 操作系统中最核心的概念就是进程,进程是对正在运行中的程序的一个抽象,是系统进行资源分配和调度的基本单位。进程是一种抽象的概念,一般由程序、数据集合和进程控制块三部分组成,如下&#x…...
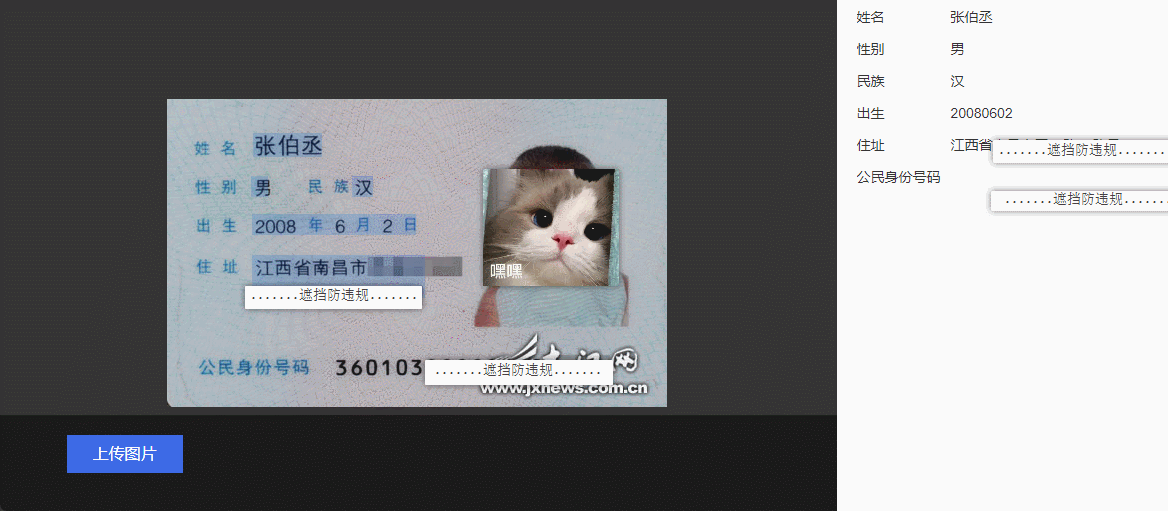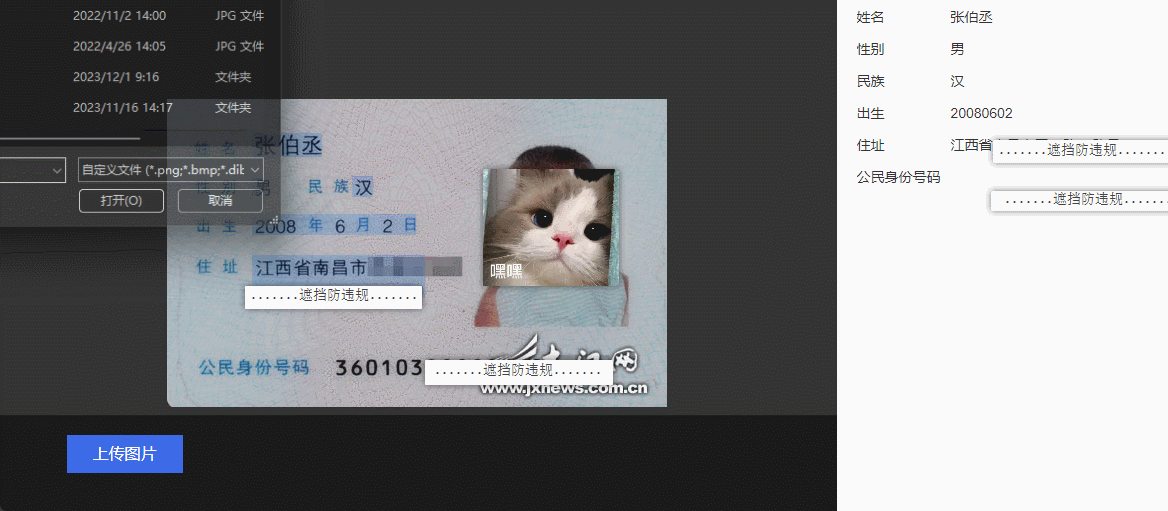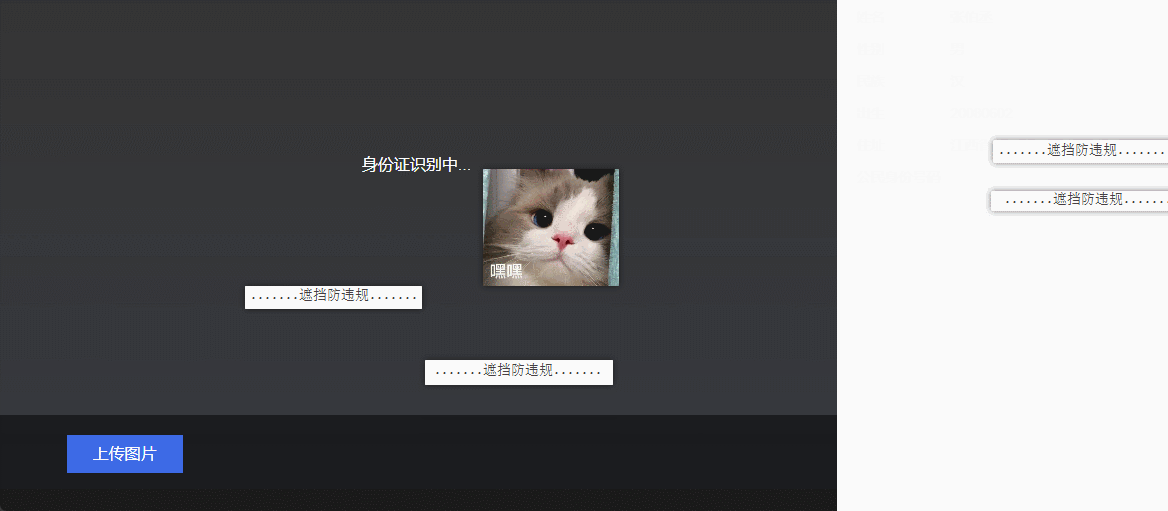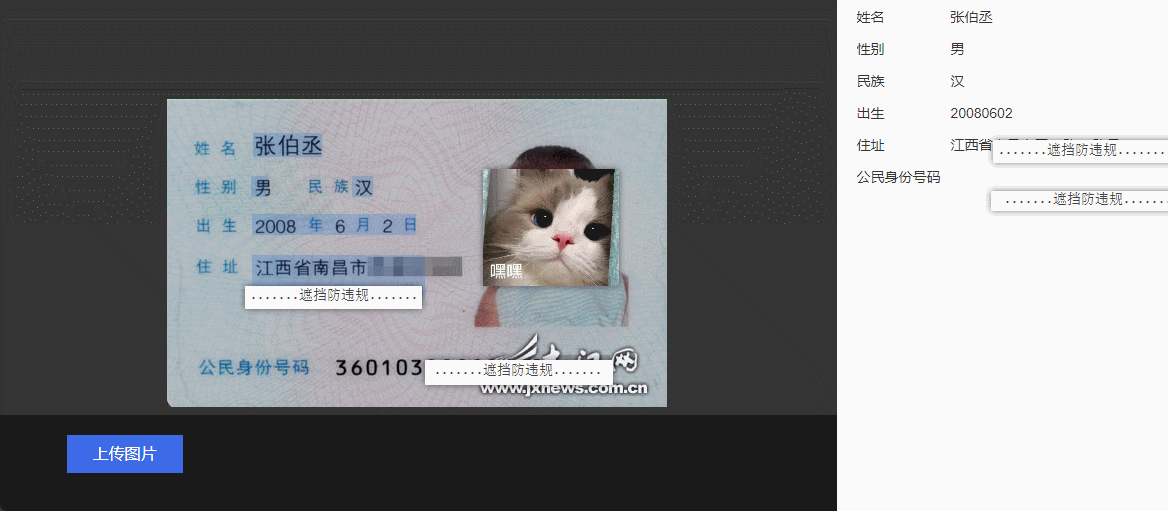
基于Python实现身份证信息识别
目录 前言身份证信息识别的背景与意义自动识别身份证的需求实现环境与工具准备Python编程语言OpenCV图像处理库Tesseract OCR引擎身份证信息识别算法原理图像预处理步骤(图像裁剪、灰度化 、二值化、去噪)信息提取与解析Python代码实现通过OCR提取身份证号码代码解析身份证信息…...
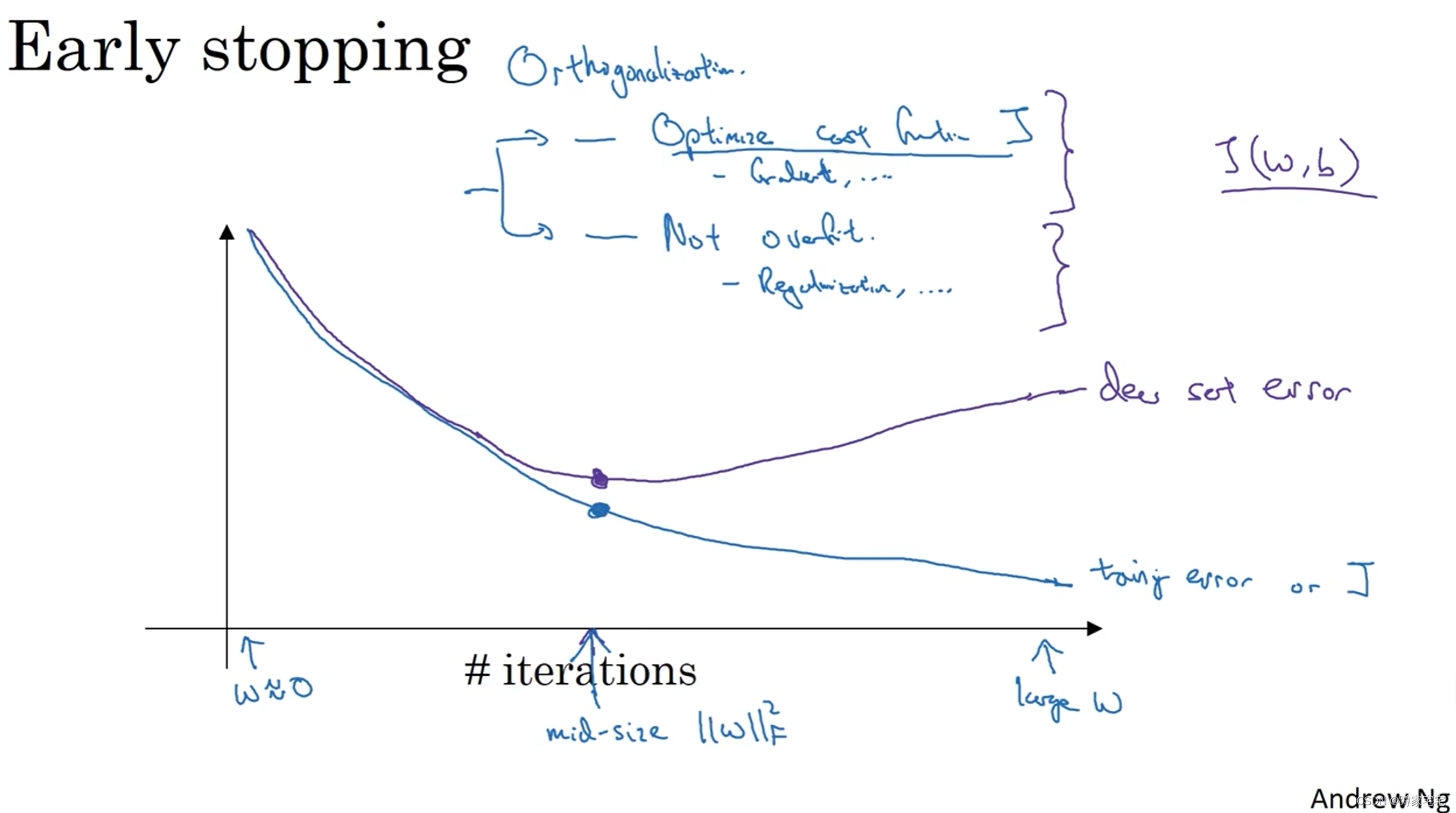
深度学习记录--正则化(regularization)
什么是正则化? 正则化(regularization)是一种实用的减少方差(variance)的方法,也即避免过度拟合 几种正则化的方法 L2正则化 又被称为权重衰减(weight dacay) 在成本函数中加上正则项: 其中 由于在w的更新过程中会递减,即权…...
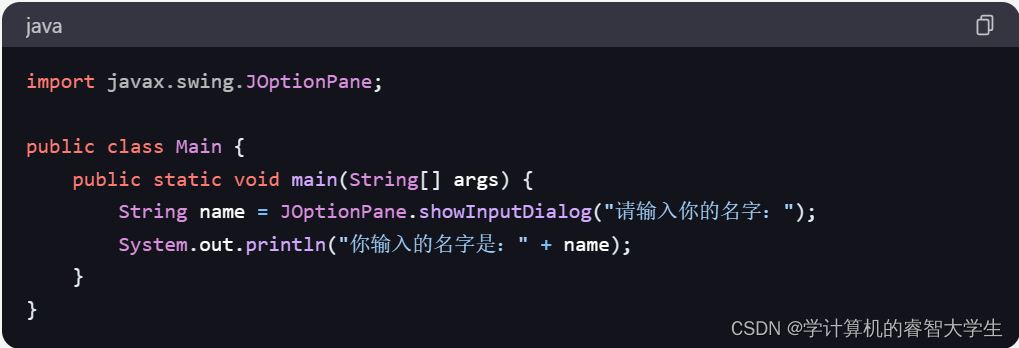
Java的便捷输入方法及解析
在 Java 中,有多种便捷的输入方法可以从用户那里获取输入。下面是一些常见的便捷输入方法及解析: 使用 Scanner 类:在上述示例中,首先导入了 java.util.Scanner 类,创建了一个 Scanner 对象,并使用 System…...
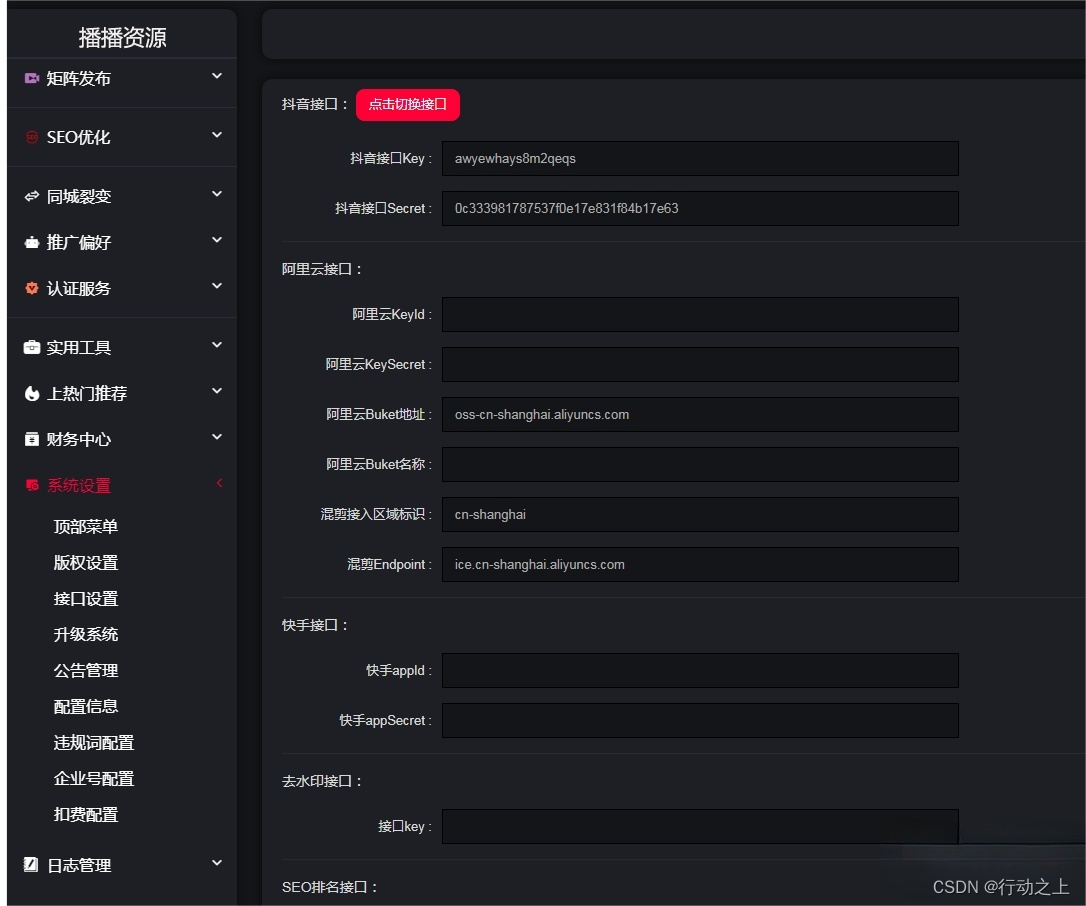
抖音矩阵云混剪系统源码(免授权版)多平台多账号一站式管理,附带系统搭建教程
搭建教程 MySQL 5.6 PHP 7.2 Apache 数据库名称 juzhen Nginx环境切换伪静态 1、解压安装包到项目根目录,找到application/database.php 更换自己的数据库密码 2、阿里云现有的配置不要动 其他按照文档进行添加 3、项目访问目录:public 4、域名…...
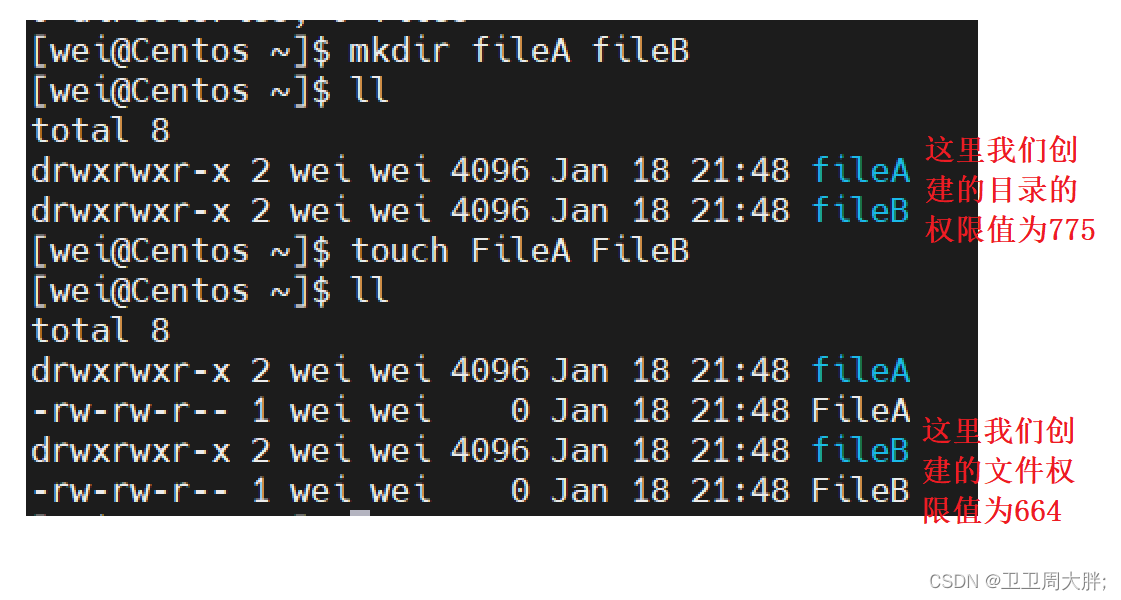
【Linux】权限的深度解析
前言:在此之前我们学习了一些常用的Linux指令,今天我们进一步学习Linux下权限的一些概念 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:Linux的学习 👈 💯代码仓库:卫卫周大胖的学习日记&a…...

c++函数怎么返回多个值
文章目录 使用结构体或类:定义一个结构体或类,其中包含了所有需要返回的值。然后在函数中返回这个结构体或类的实例。 struct Result {int value1;double value2;char value3; };Result myFunction() {Result r;r.value1 1;r.value2 2.0;r.value3 a;r…...
)
《剑指 Offer》专项突破版 - 面试题 15 : 字符串中的所有变位词(C++ 实现)
题目链接:LCR 015. 找到字符串中所有字母异位词 - 力扣(LeetCode) 题目: 输入字符串 s1 和 s2,如何找出字符串 s2 的所有变位词在字符串 s1 中的起始下标?假设两个字符串中只包含英文小写字母。例如&…...

03 SpringMVC响应数据之接收Cookie和请求头+原生API+共享域对象操作
下载postman,测试传json数据 1. 接收cookie 用CookieValue注解将cookie值绑定到控制器中的handler参数。 Controller类中的一个handler GetMapping("/CookieTest") public void handle(CookieValue("cookie的id(name)") String cookie) { //... }2. 接收…...

数据仓库(3)-模型建设
本文从以下9个内容,介绍数据参考模型建设相关内容。 1、OLTP VS OLAP OLTP:全称OnLine Transaction Processing,中文名联机事务处理系统,主要是执行基本日常的事务处理,比如数据库记录的增删查改,例如mysql、oracle…...

交换机配置及网络测试
实验环境 拓扑图 Ip规划表 部门 主机数量 网络地址 子网掩码 网关 可用ip Vlan 市场部 38 192.168.131.0 255.255.255.0 192.168.131.1 2-254 11 研发部 53 192.168.132.0 255.255.255.0 192.168.132.1 2-254 12 财务部 9 192.168.133.0 255.255.255…...
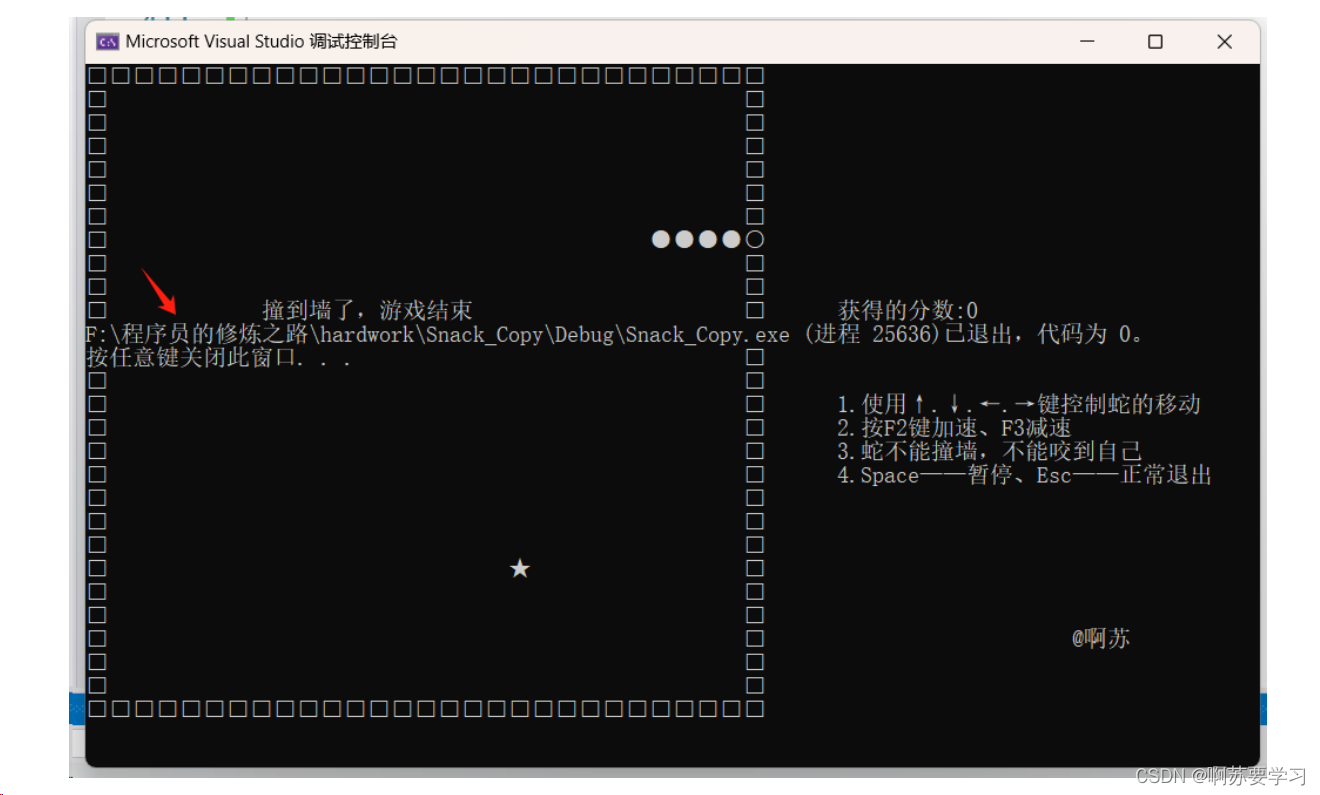
贪吃蛇游戏
文章目录 前言一.Win32API1.1GetStdHandle1.2GetConsoleCursorInfo1.3SetConsoleCursorInfo1.4SetConsoleCursorPosition1.5GetAsyncKeyState1.6setlocale二.游戏设计三.GameStart3.1蛇的创建3.2分文件3.3控制台设置3.4WelComeToGame3.5CreateMap3.6InitSnack3.7CreateFood 四.…...

DPDK trace 的简单使用
文章目录 前言trace的简单使用 前言 日志用于记录不太频繁,比较高level的事情。trace记录频繁发生的事情,它的开销低。 trace可以在运行时,通过参数控制是否启用;可以在任何时间点,将trace记录的缓冲区保存到文件系统…...
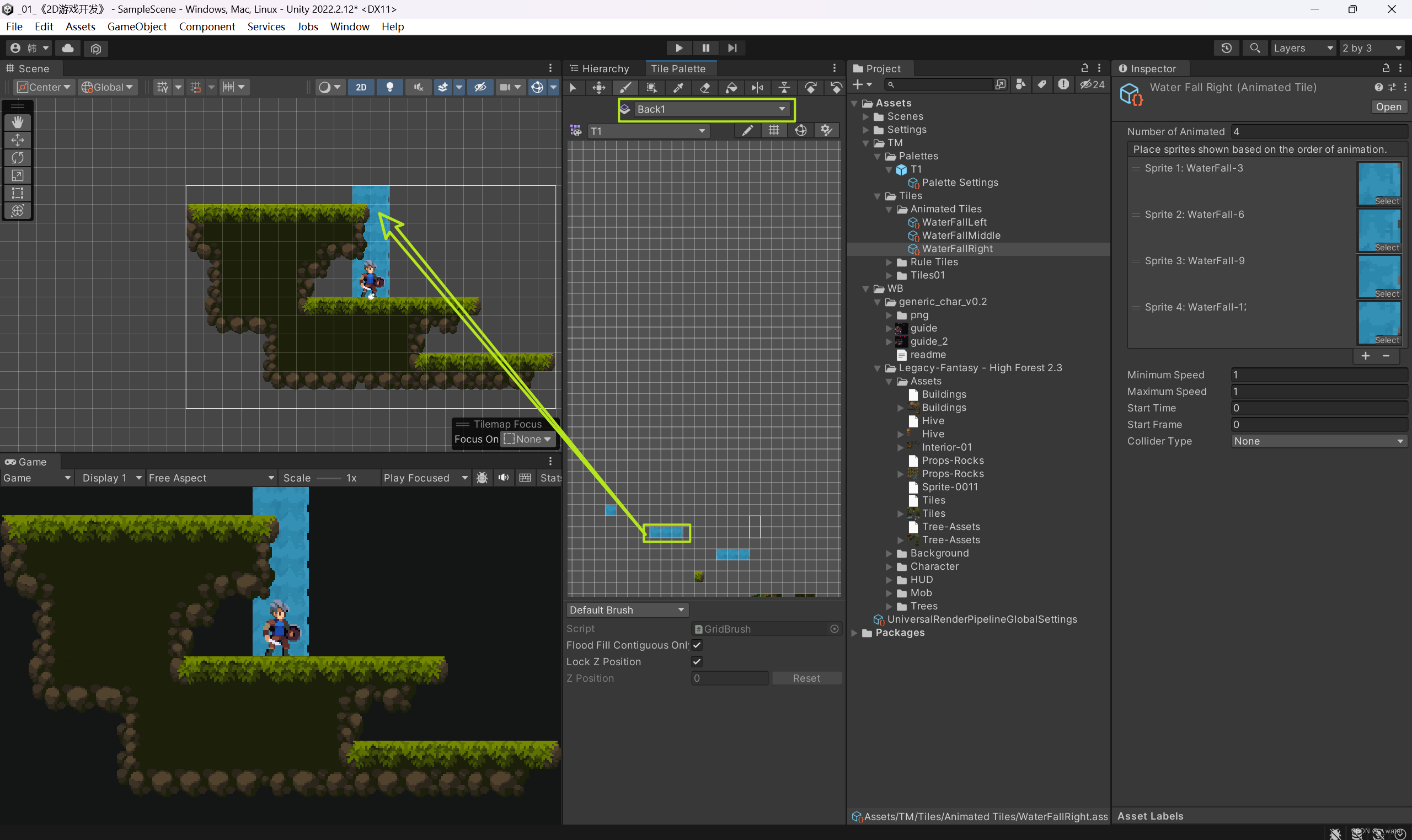
《游戏-01_2D-开发》
首先利用安装好的Unity Hub创建一个unity 2D(URP渲染管线)项目 选择个人喜欢的操作格局(这里采用2 by 3) 在Project项目管理中将双栏改为单栏模式(个人喜好) 找到首选项(Preferences)…...

如何禁用WordPress站点的管理员电子邮件验证或修改检查频率?
今天boke112百科登录某个WordPress站点时,又出现“管理员邮件确认”的提示,要求确认此站点的管理员电子邮箱地址是否仍然正确。具体如下图所示: 如果点击“稍后提醒我”,那么管理员邮件验证页面就会在3天后重新显示。 说实话&…...
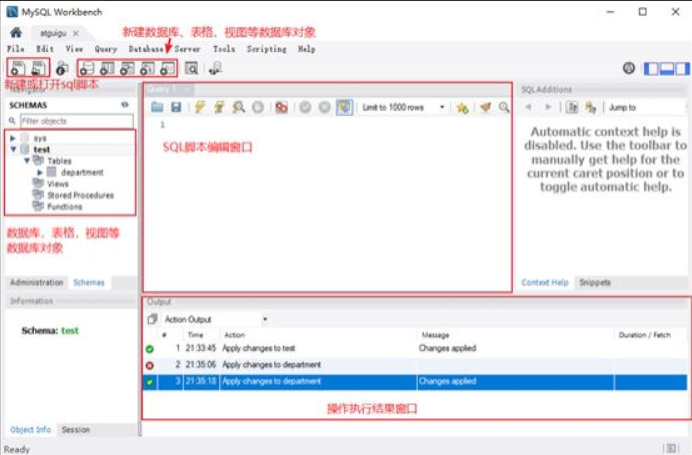
三、MySQL实例初始化、设置、服务启动关闭、环境变量配置、客户端登入(一篇足以从白走到黑)
目录 1、选择安装的电脑类型、设置端口号 2、选择mysql账号密码加密规则 3、设置root账户密码 4、设置mysql服务名和服务启动策略 5、执行设置(初始化mysql实例) 6、完成设置 7、MySQL数据库服务的启动和停止 方式一:图形化方式 方式…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
