算法刷题——拿出最少数目的魔法豆(力扣)
文章目录
- 题目描述
- 我的解法
- 思路
- 结果
- 分析
- 官方题解
- 分析
- 查漏补缺
- 更新日期
- 参考来源
题目描述
传送门
拿出最少数目的魔法豆:给定一个正整数 数组beans ,其中每个整数表示一个袋子里装的魔法豆的数目。请你从每个袋子中拿出 一些豆子(也可以 拿出),使得剩下的非空袋子中(即至少还有一颗魔法豆的袋子)魔法豆的数目相等。一旦把魔法豆从袋子中取出,你不能再将它放到任何袋子中。
请返回你需要拿出魔法豆的最少数目。
我的解法
class Solution {
public:long long minimumRemoval(vector<int>& beans) {if(beans.size() == 1) return 0;sort(beans.begin(),beans.end());long long res = LONG_MAX, temp = 0;for(int i = 0 ; i < beans.size(); ++i){temp = 0;if(i > 0) temp = accumulate(beans.begin(), beans.begin() + i, 0);for(int j = i + 1; j < beans.size(); ++j){temp += (beans[j] - beans[i]);}if(temp < res){res = temp;}}return res;}
};
思路
暴力求解,先对数组进行排序,然后从小到大分别以不同数量的豆子作为基准(非空袋子中剩下的豆子数量),求解答案。
结果

分析
时间复杂度:
O(n2)。
空间复杂度:
O(logn),即为排序的栈空间开销。
官方题解
class Solution {
public:long long minimumRemoval(vector<int>& beans) {int n = beans.size();sort(beans.begin(), beans.end());long long total = accumulate(beans.begin(), beans.end(), 0LL); // 豆子总数long long res = total; // 最少需要移除的豆子数for (int i = 0; i < n; i++) {res = min(res, total - (long long)beans[i] * (n - i));}return res;}
};
分析
时间复杂度:
O(nlogn),排序算法。
空间复杂度:
O(logn),即为排序的栈空间开销。
查漏补缺
暴力算法超出时间范围,需要思考其他的解决方案。两次循环求和可以通过总数减去一定的值得到结果(需要自己多一份思考,而不是直接暴力求解)。
更新日期
2024.01.18
参考来源
力扣链接
相关文章:

算法刷题——拿出最少数目的魔法豆(力扣)
文章目录 题目描述我的解法思路结果分析 官方题解分析 查漏补缺更新日期参考来源 题目描述 传送门 拿出最少数目的魔法豆:给定一个正整数 数组beans ,其中每个整数表示一个袋子里装的魔法豆的数目。请你从每个袋子中拿出 一些豆子(也可以 拿…...

Linux消息队列
常用函数 //创建/获取消息队列 int msgget (key_t key, int msgflg); /* key : 为键值,ftok(); msgflg:IPC_CREAT - 创建,不存在即创建,已存在即获取,除非… IPC_EXCL - 排斥,已存在即失败。 */// 向消息队列发送消息 int msgs…...

计算机网络——数据链路层(1)
一、概述 在计算机网络中,数据链路层承担着点对点通信的任务,用于跨物理层在网段节点之间参数数据。它在网络分层中处于物理层之上,网路层之下。 在链路层的讨论中,我们将看到两种截然不同类型的链路层信道。第一种类型是广播信道…...

移动端开发进阶之蓝牙通讯(四)
移动端开发进阶之蓝牙通讯(四) 在移动端开发实践中,可能会要求在不同的设备之间切换,从而提升用户体验; 或者为了提升设备的利用率,实现设备之间的连接和协同工作; 不得不通过多端连接,将多个设备连接在一起,实现设备之间的数据共享、远程控制等功能,根据具体的应用…...
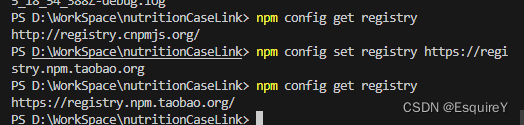
npm换源
检查现在的源地址 npm config get registry 使用淘宝镜像 npm config set registry https://registry.npm.taobao.org 使用官方镜像 npm config set registry https://registry.npmjs.org/...
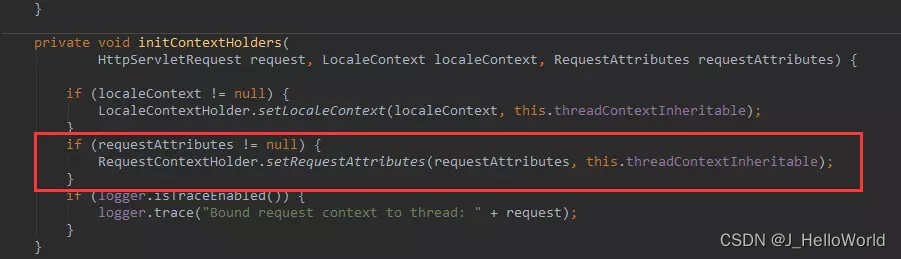
Spring 中 HttpServletRequest 作为成员变量是安全的吗?
在使用spring框架开发的时候,经常会在controller类中看到 HttpServletRequest 对象参数,一般我们都是直接使用,但是它是何时、怎么注入到 spring 容器的呢 ?另外以成员变量注入的 request 是线程安全的吗 ? Controller public c…...

浅聊雷池社区版(WAF)的tengine
雷池社区版是一个开源的免费Web应用防火墙(WAF),专为保护Web应用免受各种网络攻击而设计。基于强大的Tengine,雷池社区版提供了一系列先进的安全功能,适用于中小企业和个人用户。 Tengine的故事始于2011年,…...

如何安装配置VisualSVN服务并实现公网访问本地服务【内网穿透】
文章目录 前言1. VisualSVN安装与配置2. VisualSVN Server管理界面配置3. 安装cpolar内网穿透3.1 注册账号3.2 下载cpolar客户端3.3 登录cpolar web ui管理界面3.4 创建公网地址 4. 固定公网地址访问 前言 SVN 是 subversion 的缩写,是一个开放源代码的版本控制系统…...
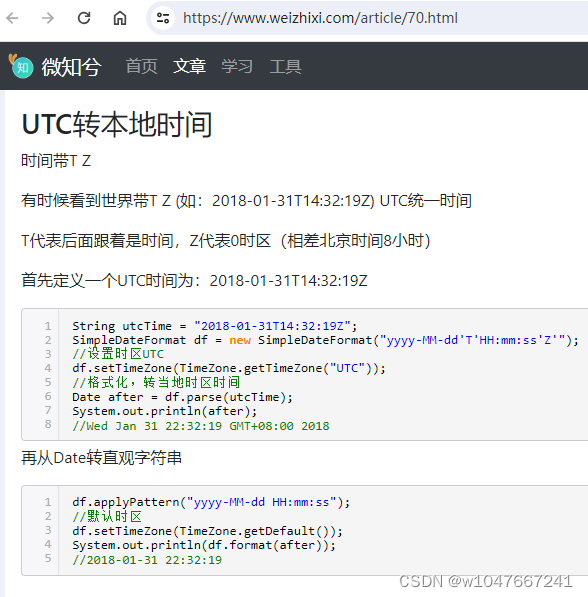
解析TZ字样的0时区UTC时间格式化为东八区
带TZ字样的0时区UTC时间格式化为东八区 TZ 的Z是zero timezone 0时区的意思。带TZ的时间是UTC0的时间SimpleDateFormat默认使用系统日历时区,必须手动指定0时区,才能正确解析TZ时间详细测试代码见下: SneakyThrows public static void main…...

python两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回…...

PBR材质背光面太暗优化
图形学中漫反射光照遵循兰伯特光照模型,它的公式如下 其中: :漫反射光颜色 :入射光颜色 :材质的漫反射系数 :法线方向 :光源方向 由于背光面的法线方向和光源方向的点积为负数,因此…...
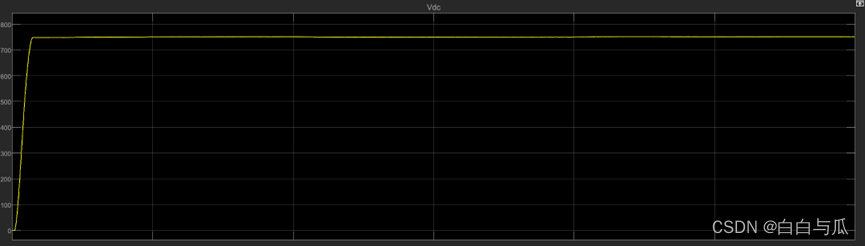
【电力电子在电力系统中的应用】6 滞环电流控制的PWM整流器 + STATCOM整流器 + APF仿真
【仅供参考】 【2023.06西南交大电力电子在电力系统中的应用】 目录 步骤一:基于滞环电流控制的PWM整流器仿真 1.1 仿真要求 1.2 仿真电路原理及设计 1.2.1 主电路的搭建 1.2.2 控制电路的搭建 1.3 波形分析 步骤二:从PWM整流器到STATCOM仿真 2…...
接近8000字的SpringSpring常用注解总结!安排
接近8000字的Spring/Spring常用注解总结!安排 为什么要写这篇文章? 最近看到网上有一篇关于 SpringBoot 常用注解的文章被转载的比较多,我看了文章内容之后属实觉得质量有点低,并且有点会误导没有太多实际使用经验的人ÿ…...
51单片机_智能家居终端
实物演示效果: https://www.bilibili.com/video/BV1bh4y1A7ZW/?vd_source6ff7cd03af95cd504b60511ef9373a1d 51单片机是否适合做多功能智能家居控制系统?51单片机的芯片是否具有与WiFi通信的能力?如果有的话,具体有哪些芯片啊&a…...

css实现动态水波纹效果
效果如下: 外层容器 (shop_wrap): 设置外边距 (padding) 提供一些间距和边距 圆形容器 (TheCircle): 使用相对定位 (position: relative),宽度和高度均为 180px,形成一个圆形按钮圆角半径 (border-radius) 设置为 50%&…...
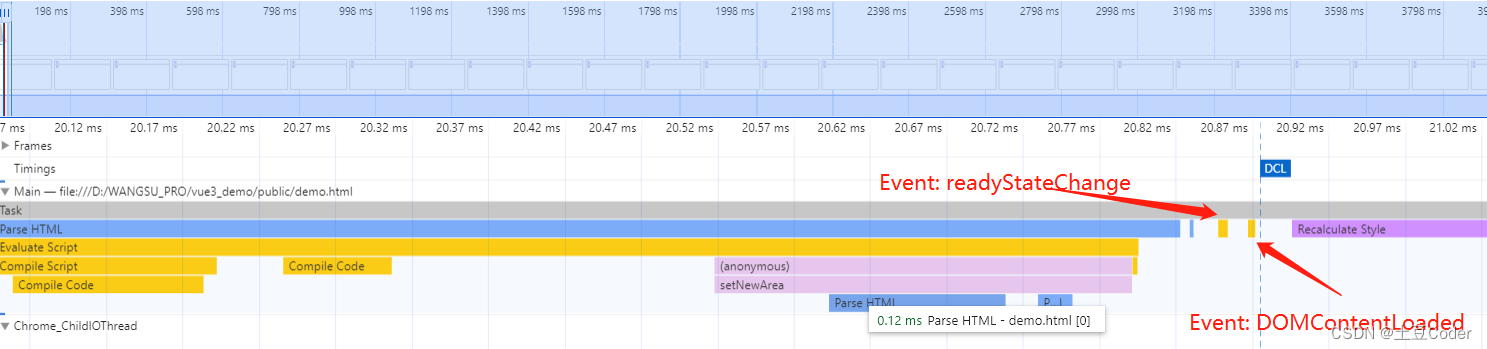
Chrome 开发者工具
Chrome 开发者工具 介绍控制面板时间线下载信息概要请求列表单个请求时间线优化时间线上耗时项 lighthouse 插件Performance(性能指标)Accessibility(可访问性)Best Practices(最佳实践)SEO(搜索…...
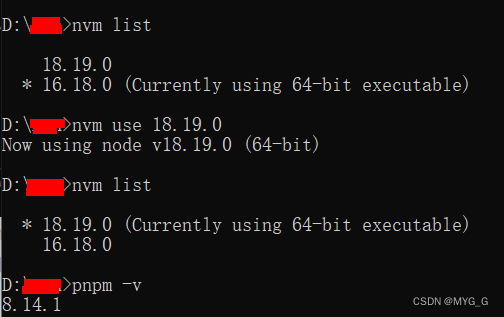
Error: error:0308010C:digital envelope routines::unsupported的解决方案
因为最近安装了pnpm对node版本有要求,升级了node版本是18以后,在运行之前的项目,就跑不起来了,报错如下: Error: error:0308010C:digital envelope routines::unsupported解决方案一: node版本切换到16版…...
vue基于spring boot框架的发艺美发店理发店管理系统的设计q9xpe
店铺信息、美发信息是发艺美发店管理系统的重要组成部分,信息清晰、详细、准确,能够有效地促进发艺美发店管理系统的运行[5]。基础设定函数是对整个系统的总体布局进行合理安排,包括:店铺活动、物品信息、领用信息等。通过对各类资…...

JS取余运算符 %,ES2023 新增数组方法Array.at
取余运算符(%)的作用就是用来两个操作数进行相除运算之后的余数。 注意,两个操作数取余是有循环范围的,这个范围为 0 - 第二个参数 - 1。 如下图: 对于6取余的话,得到的取余数据就会一直在0-5之间进行循环…...
unity SqLite读取行和列
项目文件 链接:https://pan.baidu.com/s/1BabHvQ-y0kX_w15r7UvIGQ 提取码:emsg –来自百度网盘超级会员V6的分享 using System.Collections; using System.Collections.Generic; using UnityEngine; using Mono.Data.Sqlite; using System; using Syste…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
